电容电流纹波控制Buck LED恒流驱动器研究

张留洋，徐利梅，黄影，王瑶

（西南民族大学电气工程学院，四川成都 610041）

近年来，LED作为新一代的照明光源由于其自身具有节能环保、发光效率高、使用寿命长等优点，目前已经涉及到背光源、室内外照明以及汽车照明等多个领域[1-3]。由LED的伏安特性曲线可知，若LED正向压降发生极小变化，会引起正向电流发生较大变化，导致LED亮度改变。因此，LED应采用恒流驱动方式[4-6]。

为保证LED高效、可靠工作，其驱动器应具有快速的瞬态响应速度，而驱动器的控制方法是影响负载瞬态响应速度快慢的一个重要因素[7-8]。传 统 电 压 型 控 制（voltage mode controlled，VMC）具有控制电路结构简单、抗干扰能力强等优点，但存在负载瞬态响应速度慢的问题。恒定导通时间（constant on-time，COT）控制具有控制电路结构简单、负载瞬态响应速度快的优点，但是其开关频率不固定，不利于EMI滤波器的设计与优化[9-10]。V2型控制的内环含有输出电压的信息，具有快速的负载瞬态响应速度，但是当占空比D＞0.5时会出现次谐波震荡，虽然可以采用谐波补偿技术消除，但在一定程度上会影响驱动器的负载瞬态响应速度[11]。电流型控制（current mode controlled，CMC）在VMC的电压反馈环基础上，增加了一个电流反馈环，从而提高了负载瞬态响应速度[12]。然而CMC一般采用电感电流纹波作为内环控制信号，当负载电流发生变化时，由于电感电流不能突变，对负载瞬态响应速度改善有限。相比电感电流，输出电容的电容电流可以立即变化，因此采用输出电容的电容电流纹波作为内环反馈控制信号，能更快的反应负载变化[13-16]。

为了提高Buck LED恒流驱动器的负载瞬态响应速度，基于电容电流纹波快速反应负载变化的特点，本文提出了电容电流纹波控制（capacitive current ripple-controlled，CCRC）Buck LED恒流驱动器。首先，分析Buck LED恒流驱动器的工作原理，建立状态空间平均模型。其次，阐述CCRC Buck LED恒流驱动器的工作原理，建立其小信号模型，并推导控制-输出环路增益传递函数，进而设计PI补偿参数。基于伯德图，验证PI补偿参数设计的正确性；并对比分析传统VMC和CCRC Buck LED恒流驱动器的负载瞬态响应速度。最后，通过仿真和实验结果验证理论分析的正确性。

1 Buck LED恒流驱动器

1.1 工作原理

图1为Buck LED恒流驱动器的原理图及稳态时序波形。

如图1a所示，Buck LED恒流驱动器包括：输入电压vin，电感L，开关管S，续流二极管D1，输出电容C和LED负载。其中，LED负载等效为电阻R、电压源vLED和理想二极管D2的串联。

如图1b所示，Buck LED恒流驱动器在一个开关周期T内存在两种工作状态。在[t0，t1]内，开关管S导通，续流二极管D1关断，电感电流线性上升，此为工作状态Ⅰ；在[t1，t2]内，开关管S关断，续流二极管D1导通，电感电流线性下降，此为工作状态Ⅱ。

图1 Buck LED恒流驱动器原理图及稳态时序Fig.1 The schematic and steady-state timing diagram of Buck LED constant current driver

1.2 状态空间平均模型

图1中，选取状态向量x(t)=[iL(t)vo(t)]T，输入向量u(t)=[vin(t)vLED(t)]T，输出向量y(t)=[iin(t)io(t)]T。

当驱动器处于工作状态Ⅰ时，其状态方程和输出方程分别为

当驱动器处于工作状态Ⅱ时，其状态方程和输出方程分别为

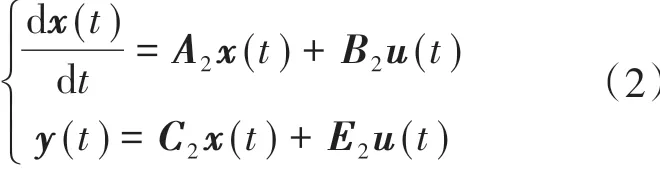
其中

式中：A1，B1，C1，E1，A2，B2，C2，E2分别为工作状态Ⅰ和工作状态Ⅱ的状态方程和输出方程的系数矩阵。

在一个开关周期内对所有变量平均化，得到Buck LED恒流驱动器的状态空间平均模型为

其中

式中：A，B，C，E为系数矩阵；d为开关管导通时的占空比。

2 CCRC Buck LED恒流驱动器

2.1 工作原理

图2为CCRC Buck LED恒流驱动器的电路原理图和控制时序波形。

图2 CCRC Buck LED恒流驱动器原理图及控制时序Fig.2 The schematic and control timing diagram of CCRC Buck LED constant current driver

图2a中，主功率电路同图1a，控制电路采用由电压控制外环和电容电流纹波控制内环组成的CCRC电路，包括：输出电流采样电阻rs1、输出电容电流采样电阻rs2、运算放大器AM、补偿器PI、比较器CM及RS触发器TM、时钟信号clk。

CCRC电路中，输出电流io通过采样电阻rs1得到输出电流采样信号rs1io，rs1io与基准电流iref比较，得到误差信号vm，vm通过补偿器PI得到误差放大信号ve，作为CCRC内环的参考信号。CCRC内环通过采样电阻rs2得到电容电流采样信号rs2ic，rs2ic与ve通过比较器比较，比较结果和时钟信号clk分别作为RS触发器TM的R端和S端输入信号，RS触发器TM的Q端输出控制信号Vgs控制开关管S，从而对驱动器的输出电流进行调节，实现LED恒流输出。其中，补偿器PI的传递函数表达式为

式中：kp，ki分别为补偿器PI的比例、积分系数。

如图2b所示，在每个开关周期的起始时刻，时钟信号clk使RS触发器TM的Q端输出高电平，开关管S导通，电容电流采样信号rs2ic以斜率k1上升；当rs2ic上升至误差放大信号ve时，RS触发器TM的Q端输出低电平，开关管S关断，rs2ic以斜率k2下降，直到下一个时钟信号到来，电路进入下一个开关周期。

2.2 小信号模型

对式（3）的状态空间平均方程和输出方程变量 施 加 小 信 号 扰 动 量其中，vin为输入电压，iL为电感电流，vo为负载LED两端的电压，vLED为负载LED的等效电压源，iin为输入电流，io为负载电流，d为开关管导通时的占空比；且大写参数为相应变量的直流分量，上标“^”为相应变量的小信号扰动量。由此可得Buck LED恒流驱动器的小信号模型表达式：

由图2b所示电容电流采样信号rs2ic的纹波波形可得：

式中：ve为误差放大信号；k1为电容电流采样信号rs2ic的上升斜率；rs2ˉic为 图2b中 阴 影 部 分 面 积 的平均值。

由式（6）和式（7）可得：

对式（8）中变量施加小信号扰动量，得到：

式中：K1为电容电流采样信号rs2ic上升斜率k1的直流分量。

由此可得占空比小信号量d̂的表达式为

其中

式中：Fv(s)，Hc(s)为传递函数。

2.3 控制-输出环路增益传递函数

根据式（5），得到CCRC Buck LED恒流驱动器的控制-输出电流传递函数Giod(s)和控制-电容电流传递函数Gicd(s)分别为

由传递函数Giod(s)，Gicd(s)，Fv(s)和Hc(s)构成CCRC Buck LED恒流驱动器的小信号模型框图，如图3所示。

图3 CCRC Buck LED恒流驱动器小信号模型框图Fig.3 Block diagram of small signal model for CCRC Buck LED constant current driver

图3中，定义x到y的环路增益函数为该驱动器的控制-输出环路增益传递函数Tc（s），其表达式为

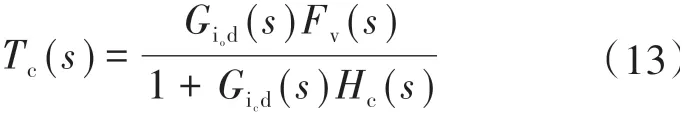
同理可得CCRC Buck LED恒流驱动器未加入补偿器PI的控制-输出环路增益传递函数Tc1（s）为

3 频域分析

3.1 PI参数设计

电路参数设置如下：输入电压vin=10 V，额定输出电压vo=3.2 V，额定输出电流io=1 A，等效电阻R=0.7 Ω，LED等效电压源vLED=2.5 V，电容C=100 μF，电感L=370 μH，开关周期T=20 μs，采样电阻rs1=rs2=1 Ω。

将上述电路参数代入式（14），可得：

由文献[11]可知，稳定系统的控制-输出环路增益传递函数的穿越频率通常为（1/20～1/5）fs，fs为开关频率。本文选取CCRC Buck LED恒流驱动器的控制-输出环路增益传递函数的穿越频率fc=（1/10）fs=5 kHz，由式（15）可得Tc1（s）的幅值裕度为

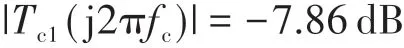
为使该驱动器稳定，需要设计补偿器PI在5 kHz处的幅值裕度为7.86 dB，即

因此，本文选取kp=2.35，可得ki=24 055。

将设置的电路参数和PI补偿参数代入式（13），得到Tc（s）的数值表达式为

依据式（15）、式（16），绘制出PI补偿前、后的CCRC Buck LED恒流驱动器的控制-输出环路增益传递函数伯德图，如图4所示。

图4 补偿前、后控制-输出环路增益传递函数伯德图Fig.4 Bode diagram of control-output loop gain transfer functions with and without compensation

由图4可知，补偿前的控制-输出环路增益传递函数的穿越频率未达到5 kHz，而补偿后的控制-输出环路增益传递函数的穿越频率为5 kHz，且对应的相位裕度为241.1°。说明PI补偿后系统稳定，PI参数设计合理。

3.2 控制-输出环路增益传递函数分析

根据式（16），利用Matlab绘制出控制-输出环路增益传递函数Tc（s）的伯德图，如图5a所示。为了验证式（16）的正确性，采用PSIM仿真软件搭建了CCRC Buck LED恒流驱动器的仿真电路，电路参数同3.1节设置。利用PSIM的交流频域仿真分析模块，对CCRC Buck LED恒流驱动器的环路增益进行扫频分析，得到基于PSIM扫频分析的控制-输出环路增益伯德图，如图5b所示。由图5可知，控制-输出环路增益传递函数Tc（s）的幅频及相频曲线与基于PSIM扫频分析的控制-输出环路增益的幅频及相频曲线基本吻合，从而验证了控制-输出环路增益传递函数Tc（s）的正确性。

图5 CCRC Buck LED恒流驱动器伯德图Fig.5 Bode diagram of CCRC Buck LED constant current driver

3.3 负载瞬态响应性能分析

根据文献[17]，可知VMC Buck LED恒流驱动器的环路增益传递函数为

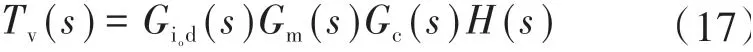
式中：Gm（s）为该驱动器的调制器传递函数；H（s）为采样网络增益。为简化计算，令Gm（s）=1，H（s）=1。

采用与CCRC Buck LED恒流驱动器相同的电路参数[9]，得到T（vs）的数值表达式为

依据式（16）、式（18），绘制出VMC和CCRC Buck LED恒流驱动器的控制-输出环路增益传递函数伯德图，如图6所示。

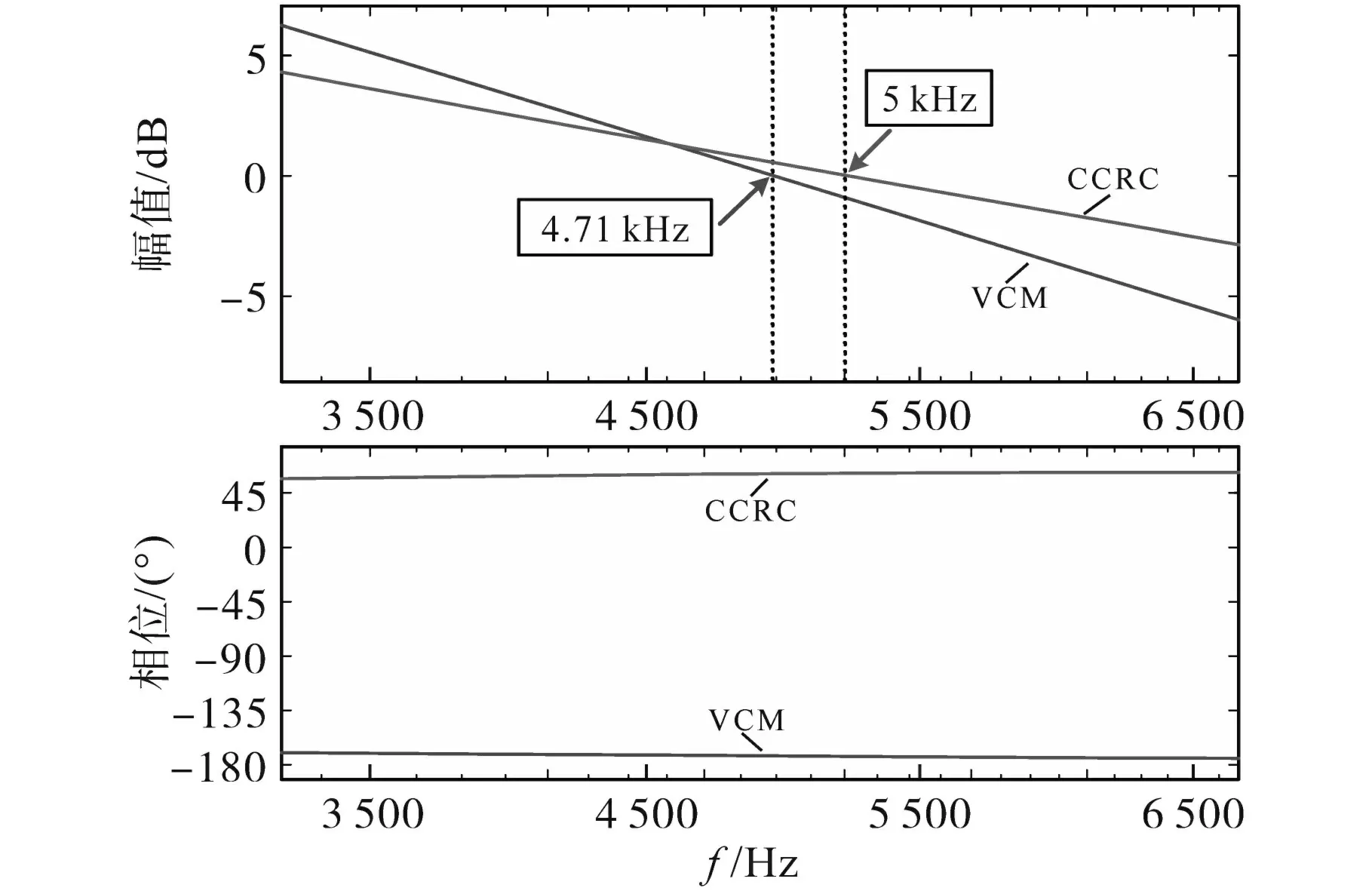
图6 VMC和CCRC Buck LED恒流驱动器环路增益传递函数伯德图Fig.6 Bode diagram of loop gain transfer functions for VMC and CCRC Buck LED constant current driver

由图6可知，VMC和CCRC Buck LED恒流驱动器的控制-输出环路增益传递函数的穿越频率分别为4.71 kHz和5 kHz。对比分析表明：相比于VMC Buck LED恒流驱动器，CCRC Buck LED恒流驱动器带宽更大、负载瞬态响应性能更好。

4 仿真验证

采用PSIM仿真软件搭建了VMC和CCRC Buck LED恒流驱动器的仿真电路，电路参数同3.1节。图7为基准电流iref变化时，VMC和CCRC Buck LED恒流驱动器的输出电流瞬态仿真波形。由图7a、图7b可知，基准电流iref从1突变至0.5时，VMC和CCRC Buck LED恒流驱动器的输出电流io1和io2均从1 A跟随变化至0.5 A；VMC Buck LED恒流驱动器的输出电流io1经过4 ms的调整时间进入了新的稳态；而CCRC Buck LED恒流驱动器的输出电流io2经过0.7 ms的调整时间进入了新的稳态。由图7c、图7d可知，基准电流iref从0.5突变至1时，VMC和CCRC Buck LED恒流驱动器的输出电流io1和io2均从0.5 A跟随变化至1 A；VMC Buck LED恒流驱动器的输出电流io1经过4 ms的调整时间进入新的稳态；而CCRC Buck LED恒流驱动器的输出电流io2经过0.45 ms的调整时间进入新的稳态；由此说明：相比于VMC Buck LED恒流驱动器，CCRC Buck LED恒流驱动器提高了负载瞬态响应速度，仿真结果与理论分析结果相符。

图7 VMC and CCRC Buck LED恒流驱动器的瞬态仿真波形Fig.7 Transient simulation waveforms of VMC and CCRC Buck LED constant current driver

5 实验验证

为了验证上述理论分析与仿真分析的正确性，采用3.1节中的电路参数，搭建了VMC和CCRC Buck LED恒流驱动器的实验电路。为了排除电容对响应速度测试的干扰，实验选取在响应速度较快的固态电容基础上作对比测试。CCRC Buck LED恒流驱动器的实验电路如图8所示，瞬态实验波形如图9所示。

图8 CCRC Buck LED恒流驱动器实验电路Fig.8 Experimental prototype of CCRC Buck LED constant current driver

图9 VMC和CCRC Buck LED恒流驱动器的瞬态实验波形Fig.9 Transient experimental waveforms of VMC and CCRC Buck LED constant current driver

由图9a、图9b可知，当基准电流iref从1突变至0.5时，VMC和CCRC Buck LED恒流驱动器的输出电流io1和io2分别经过11 ms，1.5 ms的调整时间进入新的稳态。

由图9c、图9d可知，当基准电流iref从0.5突变至1时，VMC和CCRC Buck LED恒流驱动器的输出电流io1和io2分别经过10 ms，2 ms的调整时间进入新的稳态。

由此说明：相比于传统VMC Buck LED恒流驱动器，本文提出的CCRC Buck LED恒流驱动器提高了负载的瞬态响应速度，实验结果与理论分析结果相符。

6 结论

本文分析了Buck LED恒流驱动器的工作原理，采用状态空间平均法，建立了其状态空间平均模型。提出了CCRC Buck LED恒流驱动器，阐述了CCRC Buck LED恒流驱动器的工作原理，建立了其小信号模型，推导出系统的控制-输出环路增益传递函数，并设计了控制电路的PI补偿参数。通过环路增益传递函数的伯德图，与VMC Buck LED恒流驱动器的负载瞬态响应速度进行对比分析。研究结果表明：相比于传统的VMC Buck LED恒流驱动器，CCRC Buck LED恒流驱动器具有更大的带宽和更好的负载瞬态性能。最后，仿真和实验结果验证了理论分析的正确性。