一种新型准Z源逆变器的寄生参数影响研究

韦正怡，张民，周明珠，丁新平

（1.青岛理工大学信息与控制工程学院，山东青岛 266520；2.南京信息工程大学自动化学院，江苏南京 210044）

现阶段，太阳能光伏发电得到了各国研究学者的广泛关注。在此过程中，出现了一种Z源单级可升压逆变电路[1]，目前传统Z源逆变器的分析都是基于理想的条件[2-3]，然而在实际的工作过程中，逆变器中有源、无源器件的寄生参数会对逆变器产生较大的影响，它会带来不可避免的损耗，从而降低了逆变器的工作效率[4]。

文献[5]详细介绍了准Z源逆变器及其衍生逆变器的工作效率，但所分析的逆变器结构中不包含耦合电感结构，此外对部分寄生参数的影响均进行了忽略。文献[6]针对反激型逆变电路中耦合电感做出了详细的损耗分析，但仅针对于电流型逆变器。文献[7]分析了寄生参数对Boost变换器稳定性的影响，但是仅涉及寄生参数对Boost变换器小信号模型的影响，并没有考虑在实际中寄生参数随电路损耗或工作效率的影响。文献[8]分析了氮化镓高电子迁移率晶体管（GaN high electron mobility transistor，GaN HEMT）寄生参数对全桥逆变器的损耗，但没有进行针对整个逆变器系统的寄生参数对增益以及效率亦是对其他性能方面有影响的定量分析。

本文基于所设计的一种改进Cockcroft-Walton单元改进型准Z源逆变器（modified Cockcroft-Walton modified quasi-Z-source inverter，MCWMqZSI），原理图如图1所示。该型逆变器输入电流连续，且加入耦合电感提高了升压能力，此外具有较低的器件应力等级。研究寄生电阻对逆变器的性能影响，通过精细化的寄生电阻、耦合电感漏感对逆变器电压增益、电压应力以及工作效率影响的分析，并依据定量分析各寄生电阻对逆变器性能影响的结果，为新型逆变器的参数设计以及性能改善提供理论依据。

图1 MCWM-qZSI电路原理图（不考虑寄生参数）Fig.1 The schematic diagram of the MCWM-qZSI circuit（without parasitic parameters）

1 逆变器的稳态工作状态

1.1 不考虑寄生参数的稳态分析

为了简化分析，将图1中MCWM-qZSI的工作状态分别等效为直通状态与非直通状态。

借助参考文献[2]中的方法，对图1中直通状态与非直通状态下存在的电压关系利用伏秒平衡以及安秒平衡法则，可以得到MCWM-qZSI的电压增益为

式中：n为耦合电感匝数比；D为直通占空比。

此外，将求解得到的主要器件电压、电流应力分别总结于表1与表2中，其中，Sh为开关器件，h=1，2，…，6；Iin为输入电流。

表1 主要器件的电压应力Tab.1 Voltage stress of the main components

表2 主要器件的电流应力Tab.2 Current stress of the main components

1.2 寄生参数下逆变器的稳态分析

图2为寄生参数下MCWM-qZSI的等效电路图。其中rL1，rN21，rN22分别为输入电感L1、绕组N21，N22上的寄生电阻；rC为电容上的寄生电阻；UF为二极管正向导通时存在的压降；RF为二极管直通时刻的等效电阻；rDS为开关管的导通电阻；Co为六个开关管中二极管的等效结电容。

图2 MCWM-qZSI等效电路图（考虑寄生参数）Fig.2 MCWM-qZSI equivalent circuit diagram（considering parasitic parameters）

同理，可以分析图2在直通状态与非直通状态时的电压关系为

式中：UL1_on，UL1_off分别为电感L1在直通与非直通时的电压；ish为开关管瞬时电流；UN21_on，UN21_off，UN22_on与UN22_off分别为耦合电感原、副边在直通与非直通状态时的电压。

对式（2）、式（3）利用伏秒平衡法则，并借助表1，可以得到寄生参数条件下MCWM-qZSI的电压增益为

其中

式中：R为输出端所接负载的等效电阻。

将式（4）中与寄生参数相关的数值忽略，其值与式（1）相同，验证了公式推导的准确性。

2 寄生电阻对MCWM-qZSI增益及电压应力的影响

2.1 对增益的影响

从式（4）可以看出，逆变器的电压增益不仅与直通占空比D相关，还与逆变器的寄生电阻、耦合绕组的匝数比以及等效阻抗R有关。

为了直观分析不同器件上寄生电阻对电路性能的影响，在保持匝数比n和负载等效阻抗R不变的情况下，令各器件的寄生参数数值如下所示：

rDS=0.024 Ω，Co=15 nF，RF=0.008 Ω，UF=1.25 V，rL1=0.1 Ω，rC=0.01 Ω，rN21=0.022 5 Ω，rN22=0.027 5 Ω。依据Case1～Case7的变化趋势，绘制增益B*随占空比D变化的关系曲线，如图3所示。

图3 不同寄生参数条件下MCWM-qZSI电压增益曲线Fig.3 MCWM-qZSI voltage gain curves diagram under different parasitic parameters

图3中，Case1～Case7情形参数变化定义如下：

图3中，曲 线（1）～曲 线（7）分 别 代 表Case1～Case7这7种情况。曲线（1）作为原始数据的曲线，对比剩余6条曲线，可以得到如下结论：

1）所有曲线的趋向都相似，即B*的值会随D的提高而变大，且当D到达一定值后，B*会被迅速拉低，这就是极限升压倍数。因此，在电路设计时，要注意极限占空比的存在，通过调整匝比以避免电路运行在这个工作状态导致系统性能下降和电路故障甚至安全事故。

2）对比所有的相邻曲线，曲线（3）～曲线（5）与曲线（1）之间的纵向差值最大，这是分别将电容、开关管和输入电感中存在的寄生电阻去掉后造成的。由此可知，这三种器件上的寄生电阻对实际电路升压能力干扰程度最强。

3）总体来看，寄生电阻的存在对逆变器处于小占空比（小升压倍数）时的影响没有特别大，但是随着占空比的升高，电路的升压能力增强，寄生电阻对升压因子的影响程度越来越明显，尤其是在到达极限占空比附近效果最为明显。

4）从曲线（5）可以看出当电感L1的寄生电阻为0时，此时逆变器的电压增益较大，也可以看出电感的寄生电阻对逆变器的影响。因此，在进行样机设计时，需要充分考虑到输入电感寄生电阻的影响，进行合理的器件设计选型，从而保证逆变器能够有较高的工作效率。

综上，在设计样机时，要尽量选择寄生电阻小的器件，从而保证所设计逆变器满足高增益高性能指标要求。与此同时，需要注意极限占空比的存在，避免出现安全事故问题。

2.2 对电压应力的影响

逆变器中各个器件上的电压应力也是衡量电路特性的一个重要指标，通过电压应力等级参数选择合适的器件可以有效地提高电路工作性能，确保电路能够安全稳定的工作。下面通过定量分析MCWM-qZSI中主要器件的寄生参数对其电压应力的影响，从而为器件的选型提供理论依据。为了简化分析，这里仅分析电容C1上的寄生电阻对其电压应力的影响。

对式（2）、式（3）利用伏秒平衡法则，可以得到寄生电阻条件下C1的电压应力如下式所示：

其中

将公式（5）中各个寄生参数值理想化，则结果与表1中寄生参数理想化时电容C1的电压应力公式一致，进一步验证出公式推导的正确性。

为了直观分析寄生电阻对电容C1电压应力的影响，在保证匝比n、输入电压Ug以及等效负载R不变的条件下。利用以下参数变化趋势（CaseⅠ～CaseⅢ）画出了电容C1的电压应力随占空比D变化的关系曲线，如图4所示。

图4 不同寄生参数条件下MCWM-qZSI中电容C1的电压应力Fig.4 Voltage stress of capacitor C1 in MCWM-qZSI under different parasitic parameters

从图4中可以发现，随着寄生参数的不断变大，MCWM-qZSI中电容C1的电压应力反而变小。相反，当完全将器件的寄生参数理想化时，电容C1的电压应力反而很大。对于本文中的MCWMqZSI而言，较大的寄生参数降低了器件的电压应力，为逆变器提供较好的工作性能，然而对于不同结构的逆变器而言较大的寄生参数也可能会产生较大的应力，为逆变器带来不必要的损耗。

较大的寄生参数虽然会为某些电路带来较小的电压应力，但是也会产生大量的损耗，降低逆变器的工作效率。因此，为了既能够保证逆变器具有较为理想的效率，又能带来较小的电压应力，综合考虑并合理的选择器件是十分重要的。这也为改善逆变器整体工作效率、样机设计及器件选型提供了理论依据。

3 寄生电阻对MCWM-qZSI效率的影响

下面分别讨论不同器件寄生电阻、等效串联电阻（equivalent series resistance，ESR）对逆变器带来的功率损耗以及效率的影响，从而为器件的选型以及样机性能改进提供依据。

3.1 开关管的功率损耗

开关管的瞬时电流可以近似为

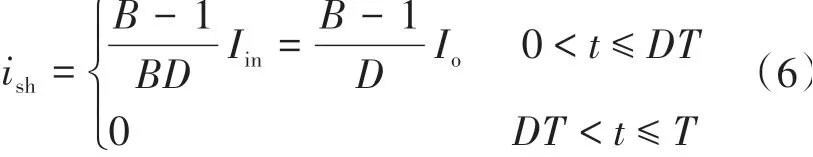
式中：Io为输出电流；T为采样周期。

于是可以得到一个周期中的电流有效值为

式中：PPN为逆变器的输出功率；UPN为直流母线输出电压；IPN为直流母线输出电流。

由于直通时所有开关管都处于导通状况，所以流过每组桥臂上的电流等于1/3Ish，于是直通时刻逆变桥上开关管总导通损耗为

开关管关断损耗为

式中：Co为等效结电容；CDE为集射极间结电容；USM为开关管关断时电压，此处为直流母线输出电压。

开关管的总损耗为

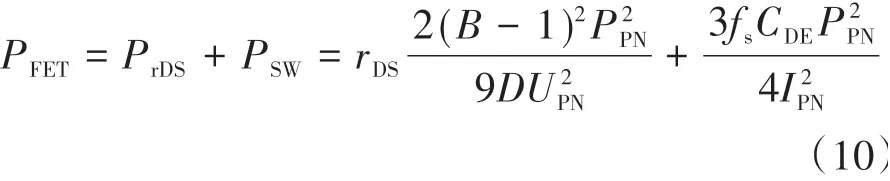
3.2 二极管的功率损耗

同理，根据以上步骤与表2中的电流关系求解出二极管的瞬时电流，并得到其导通损耗为

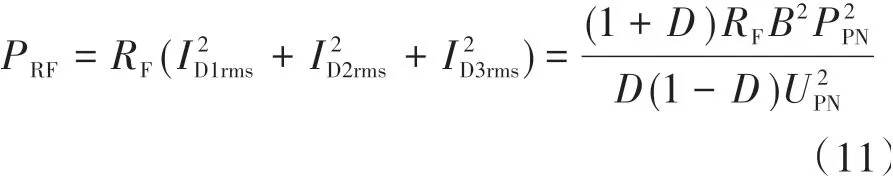
二极管平均电流为

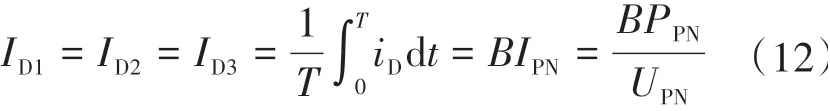
从而可得二极管上的开关损耗为

综上，二极管的总损耗为

3.3 电感的ESR功率损耗

同理，根据表2可得电感上的瞬时电流，并进一步求解出其电流有效值为

综上，可得电感上的ESR功率损耗为

3.4 电容的ESR功率损耗

同理，根据以上计算步骤与表2中的电流关系，可以得到一个周期内电容上的电流有效值为

因此，电容上的ESR功率损耗为

3.5 逆变器的工作效率

根据上述计算过程，MCWM-qZSI的总功率损耗为

因此，电路的总效率可以表示为

3.6 逆变器效率性能分析

为了直观分析逆变器的效率关系，绘制出MCWM-qZSI在不同开关频率下的工作效率随输出功率变化的曲线（取升压因子B=4，占空比D=0.125），如图5所示。

图5 寄生参数条件下MCWM-qZSI的效率曲线Fig.5 MCWM-qZSI efficiency curves with parasitic parameters

从单一曲线的角度出发，显然系统整体效率呈现随输出功率的升高先提升后又降低的趋势，当输出功率为350 W时，此时逆变器的效率最高，大约为90%。

从不同开关频率的角度来看，逆变器的工作效率会随着直通开关频率的不断增加有不同程度的减小。如果开关频率过高，这样会严重影响逆变器的效率。在接下来的分析和实验验证中，取折中的直通开关频率，fS=20 kHz，这样既能减小输入纹波和电感体积，同时还能保证不错的效率。

图6为输出功率达到1 000 W时，不同器件的功率损耗占总损耗的比例，其对电路效率的影响程度由大至小为：二极管损耗PD（35%）=电感损耗PrL（35%）＞电容寄生电阻（ESR）损耗PrC（21%）＞开关管损耗PFET（9%）。从图6中可以看出：电感和二极管上的损耗占比最大，共有70%的占比。在器件选型时，要尽可能的选择寄生参数小的型号。此外，对输入电感以及耦合电感在设计时提出更高的要求，确保寄生参数达到理想的标准。可以通过多股并绕、采用较粗的铜线、使用低电阻率的导线等方法来降低输入电感以及耦合绕组侧的寄生电阻。

图6 功率损耗占比Fig.6 Proportion of power loss

根据式（20）能够绘制出逆变器效率与D的变化趋势，如图7所示，其中，各种寄生参数的变化趋势情况（case1～case7）同上述对增益分析时一致。

图7 占空比D与效率η关系曲线Fig.7 The relationship curves between duty cycle D and efficiency η

从图7中能够发现，曲线在占空比小于0.11时下降的趋势很慢，但是在占空比大于0.11之后开始被迅速拉低，这也从除了调制比之外的另一个角度上验证了在这类逆变器设计时占空比不能设置太大。将曲线（1）作为参考，对比其他曲线，其中曲线（3）位于所有曲线的最上方，这表示去除电容的寄生电阻对逆变器效率的提升效果最好。而其他曲线分布比较密集且与曲线（1）也是有一定的纵向距离，表示去除其他器件的寄生参数对效率提升的效果相差不大，但是对逆变器的工作效率有一定程度的影响。

4 漏感对MCWM-qZSI的影响

随着耦合电感的引入，耦合电感中分布的漏感量也会对电路性能产生影响。在此，将主要讨论耦合电感的漏感对MCWM-qZSI电压增益的影响。其电路工作模态等效图如图8所示。图8中，Lk-N21，Lk-N22分别表示耦合电感原、副边的漏感。

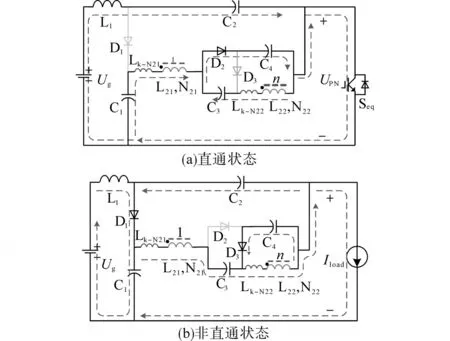
图8 考虑漏感的MCWM-qZSI等效电路图Fig.8 MCWM-qZSI equivalent circuit diagram considering inductance

根据图8中所示的直通、非直通状态，可以得到以下电压关系：

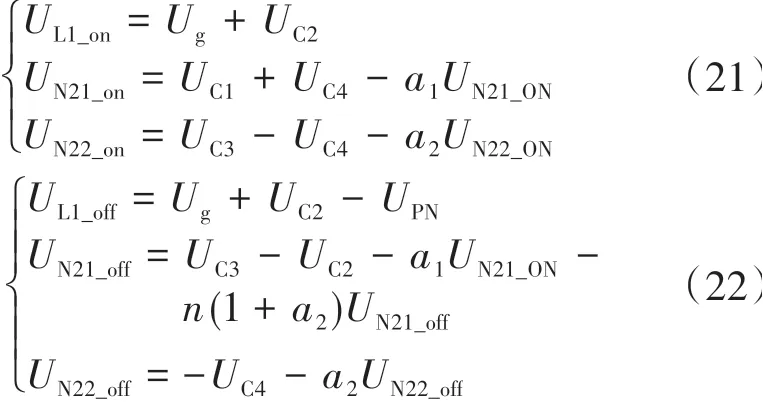
式中：a1，a2分别为耦合电感原边N21与副边N22的漏感系数。

利用式（21）、式（22）对L1以及N21使用伏秒平衡可以得到考虑耦合电感漏感条件下的电压增益为

同理，为了直观分析耦合电感漏感对逆变器增益的影响，固定匝比n为1。绘制出几种不同漏感参数下，MCWM-qZSI的增益随占空比D变化的关系曲线，如图9所示。

图9 漏感量与升压因子的关系曲线Fig.9 The curves between the leakage inductance and the boost factor

从图9中也可以看出耦合电感原边漏感Lk-N21对逆变器增益的影响要比副边漏感Lk-N22的影响大，较大的原边漏感可以带来较大的增益。

但是从逆变器的模态分析中可以发现，二极管D1两端的电压等于直流链输出电压UPN，如下式所示：

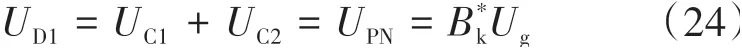
如果为了获得较高的增益而提高漏感量的话，会导致二极管D1两端会产生较大的电压尖峰，危及样机的安全性。因此，我们需要根据理论分析结果合理设计漏感量的大小，确保所设计的电路能够最大限度地产生优良的性能。这也为电路设计提供了理论依据。

5 实验

为了进行实验测试验证，构建一个输出功率等级达到1 000 W的样机，并采集相应的实验波形。

实验参数如下所示：Ug=100 V，输出功率Pout=1 kW，L1=800 μH，励磁电感Lm=462 μH，n=1，调 制 因 子M=0.88，D=0.125，C1=C2=C3=680 μF，C4=1 000 μF，开关频率fsh=20 kHz，R=40 Ω，rL1=0.1 Ω。

图10为M=0.88，D=0.125时的样机实验波形图，根据图中的波形可知新型逆变器的输出电压UPN为316 V，输出三相电的频率为60 Hz，且其电压幅值在170 V左右，有效值为120 V，且各个关键器件上的电压应力也与理论分析时一致。

图10 样机实验波形Fig.10 Experiment waveforms of the prototype

此外，通过绕制不同寄生电阻值的输入电感进行样机实验，采集不同功率等级下的实验效率曲线如图11所示。由图11可知，输入电感的寄生电阻越大，样机效率越低。所以在进行输入电感的设计时可以通过多种方法降低输入电感的寄生电阻，减少逆变器的损耗，提高逆变器的工作效率。

图11 逆变器实验效率曲线Fig.11 Inverter experimental efficiency curves

6 结论

本文分析了MCWM-qZSI中各个器件寄生电阻以及电路中存在的漏感量对逆变器电压增益、工作效率以及电压应力方面的影响。最后，通过所设计的1 000 W样机实验结果以及实验波形，证明了较优的寄生参数对逆变器性能改善的重要性。

该定量研究可为逆变器的设计提供理论依据，通过合理的器件选型以及减少器件寄生参数的优化设计方法，保证了电路的理想性能指标。

与此同时，除了器件的寄生参数影响外，样机电路板的设计也会对电路的性能产生影响，例如理想的环路设计可以有效降低寄生电感，改善开关管的电压尖峰，避免出现安全问题等。