例谈法向量在立体几何中的应用
江苏省清江中学(223001)赵丽云
空间向量与立体几何是高中数学的重点内容,也是高考的必考知识点。空间向量法在立体几何中的应用,从某个角度看,就是法向量在空间几何中的应用。空间向量法可大大减少几何思维量,但增加了运算量。所谓平面的法向量,就是垂直于平面的空间向量。法向量是破解各类立体几何问题的有效工具,它不仅可以帮助解题者判断或证明空间基本图形的位置关系,还可以帮助解题者计算空间距离和空间角以及解决立体几何探索性问题。
一、利用法向量证明线面平行、面面平行
将立体几何置于空间直角坐标系中,可以通过平面向量的坐标运算来证明空间平行关系,包括线面平行和线线平行。线面平行,只需证明直线的方向向量与平面的法向量垂直,而证明面面平行,则只需证明它们的法向量互相平行。
[例1]已知正方体ABCD-A1B1C1D1的棱长为2,E、F分别是BB1,DD1的中点,求证:(1)FC1∥平面ADE;(2)平面ADE ∥平面B1C1F。
证明:如图1所示建立空间直角坐标系D-xyz,则有D(0,0,0),A(2,0,0),C(0,2,0),C1(0,2,2),E(2,2,1),F(0,0,1),所以


点评:无论是证明线面平行,还是面面平行,关键是找到相关平面的法向量。当建立空间直角坐标系后,一般可采用方程思想求出法向量的坐标,通过坐标运算来证明或验证平行关系。
二、利用法向量证明线面垂直、面面垂直
将立体几何置于空间直角坐标系中,同样可以利用空间向量的坐标运算证明垂直关系。要证线面垂直,只需证明直线的方向向量与平面的法向量平行;而要证面面垂直,则只需证明它们的法向量互相垂直。
[例2]已知正方体ABCD-A1B1C1D1中,E是BB1的中点,F是CD的中点。
求证:(1)D1F⊥平面ADE;(2)平面A1D1F⊥平面ADE。
证明:(1)如图2 所示建立空间直角坐标系D-xyz,令AA1=2,则D(0,0,0),D1(0,0,2),A(2,0,0),E(2,2,1),F(0,1,0),

图2


点评:利用法向量证明垂直关系与利用法向量证明平行关系“惊人相似”,解答的关键是利用坐标法求出相关平面法向量的坐标,进而通过平面向量数量积坐标运算加以验证。
三、利用法向量求线面夹角、面面夹角
将立体几何置于空间直角坐标系中,处理斜线与平面所成的角,只需先求出斜线和这个平面的法向量的夹角,因为这个角和直线与平面所成的角互余,所以很容易求出斜线与平面所成的角;而对于二面角的平面角的求解,通常可先求出它们的法向量的夹角,因为这个夹角或者它的补角就是所要求的二面角的平面角,具体取舍哪个,要看图形而定。
[例3]已知正方体ABCD-A1B1C1D1中的棱长为2,
(1)求直线AD与平面A1BC1所成的角的正弦值;
(2)求平面A1B1C1D1与平面A1BC1所成的二面角(锐角)的余弦值。


图3


点评:空间角是有范围的,当它表示特殊角时可用反三角函数来表示。本例第(2)问已经注明所求的二面角是锐角,否则它也可能是而线面角与线线角都不可能是钝角,尤其是求线线角时,若利用法向量计算的角的余弦值为负,则应转负为正。
四、利用法向量求空间距离
在立体几何中空间距离有点面之距、线面之距、面面之距等。将立体几何置于空间直角坐标系中,空间距离同样可以利用空间向量的坐标来求得,但必须先求出该平面的法向量的坐标。求点面之距,可先求经过这点的某斜线段的长m,再求该斜线与平面的法向量所成的角θ,于是所求距离d=msinθ;而面面之距与线面之距都可转化为点面之距来求得。对于两异面直线之间的距离,可先求它们的公共法向量,再在两条直线上分别各取一点,那么过这两点的向量在法向量上的射影的长度即为所求。
[例4]如图4的正方体ABCD-A1B1C1D1中,

图4
(1)求点B1到平面A1BC1的距离;
(2)求A1B与B1C之间的距离。
解析:(1)由例3 知=(1,1,1)是平面A1BC1的一个法向量,设点B1到平面A1BC1的距离为d,则


设A1B与B1C1间的距离为d,则

点评:利用法向量求空间距离,通常将其转化为求直角三角形的一条直角边长来处理,因此可利用坐标法求出该直角三角形的斜边和法向量与该斜边所在的向量的夹角的余弦值。
五、利用法向量求解立体几何探索性问题
立体几何的探索性问题,通常要求解题者在动态中探求符合要求的空间元素的位置。平面的法向量的方向虽然是固定的,但它是自由向量,在求解立体几何的探索性问题时引入法向量,能够帮助解题者快速解决问题。
[例5]如图5,在直三棱柱ABC-A1B1C1中,已知侧面AA1B1B是正方形,AB=BC=2,E,F分别为AC和CC1的中点,D是棱A1B1上 的 点,且 满 足BF⊥A1B1。问当B1D为何值时,面BB1C1C与面DFE所成的二面角的正弦值最小?

图5
解析:∵三棱柱ABC-A1B1C1是直三棱柱,∴BB1⊥底面ABC,∴BB1⊥AB。∵A1B1∥AB,BF⊥A1B1,∴BF⊥AB,又BB1⋂BF=B,∴AB⊥平面BCC1B1,∴BA,BC,BB1两两垂直。以B为坐标原点,分别以BA,BC,BB1所在直线为x,y,z轴建立空间直角坐标系,如图6,∴B(0,0,0),A(2,0,0),C(0,2,0),B1(0,0,2),A1(2,0,2),C1(0,2,2),E(1,1,0),F(0,2,1)。由题设D(a,0,2)(0 ≤a≤2)。
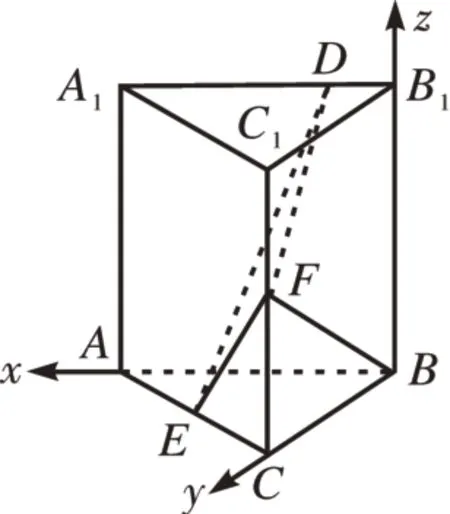
图6

令z=2 -a,则m→=(3,1 +a,2 -a),∵平 面BCC1B1的法向量为=(2,0,0),设平面BCC1B1与平面DEF的二面角的平面角为θ,

点评:本题主要考查空间向量的相关计算,在求解时,利用法向量的特征建立二面角余弦的函数关系,从而求得二面角的余弦值的最大值,进而找到正弦值最小值,由此求出B1D的长度。
由此可见,坐标化的立体几何为法向量的应用开辟了广阔的道路,让法向量有了“用武之地”。法向量除了可以解决以上四类问题,还可以解决立体几何的探索性问题,这里限于篇幅,不再详细阐述。值得一提的是,无论是利用法向量解决立体几何中的哪种问题,关键是准确无误地求出法向量的坐标,把原问题坐标化,将几何问题转化为代数问题。

