乡村小学生数学语言表达能力培养探究
☉陈时琰
数学语言能反映出学生的思维水平。在教学中,一方面学生需要从学会应用标准的数学语言描述数学问题这一渠道出发,逐渐发现思维存在的问题;一方面学生需要接受系统的思维训练来优化数学语言应用。部分乡村学生的数学基础比较差、思维水平不高,他们需要教师给予专门的数学语言表达训练。
一、结合模板学习数学语言表达方法
虽然部分小学生不知道如何应用数学语言来描述生活中的数学问题,但是他们擅长模仿学习。在开展教学时,学生可以结合教师给出的既有模板来描述数学问题。在长期接受模板训练,学生掌握了这种数学语言描述的方法以后,他们就能够慢慢脱离模板,正确地应用数学语言描述问题。以《认识人民币》的教学为例[1]。
(一)描述问题的数量关系
部分学生在遇到生活中的问题时,不知道怎么提取生活问题中的数学材料,更不知道要用什么样的语言来描述数学问题,从而导致部分学生不会在具体的情境中描述数学应用题,也不会分析数学应用题中给出的材料。教师需要引导学生学会描述生活问题中的数量关系。
教师为学生展示出不同数额的人民币图片,图片中包含大量50元、20元、10元和1元面值的人民币和1分、2分,5分、1角、2角和5角的人民币辅币。然后教师建立以上模板。
问题1:请说出以上人民币的面额。
以上人民币的面额有50元、10元……(剩下由学生自己补充)
问题2:请说出以上不同面额人民币的数量。
以上50元人民币的面额共有( )张、20元人民币面额共有( )张……(剩下由学生自己补充)
问题3:以上的人民币加起来有多少呢?
50元人民币的面额共有( )张+20元人民币面额共有( )张=( )元人民币
问题4:结合以上的学习案例,你觉得什么是提取数学问题的数量关系?
学生开始思考和分析,结合以上的学习经验,他们认为提炼数学材料中数量关系的方法,首先就是要了解他们需要探讨一个什么数学问题。例如,在人民币数量问题上,他们要探讨的就是在情境中人民币有多少张或多少元(角、分)的问题。结合问题探讨的需求,他们需要提炼数学材料的数与量的信息。
部分小学生在探讨数学问题的时候,不能了解生活问题与数学问题的差异,不会应用数学语言来描述事物,于是他们的描述存在漏洞。在这一则案例中,教师应用案例让学生看到生活语言的描述和数学语言的描述存在着差异。通过案例学生看到,他们在生活中描述人民币有时会说:“这东西多少钱?”“这本书几块钱?”,在生活中人们常常默认“钱币”就是“人民币”,而“块”就是“元”的意思,而在数学问题的探讨中,数学语言要求学生应用准确、无歧义的语言来表达数学问题,于是学生需要应用正确的数学概念来描述事物。
(二)描述问题的逻辑关联
当学生提炼出了数学问题中的数量关系以后,学生需要建立数量关系的关联。而这一环节的训练,能够反映出学生数学建模的水平。在小学阶段,学生需要学会应用简单的数学算式建立数量关系之间的关联,完成数学问题的描述。
例如,教师继续展示不同人物手持不同面额人民币的图片,为学生建立模板:爸爸手中有15元、妈妈手中有28元,我手中有13元,请问我们一家人加起来有多少元?然后引导学生明确:以上已知条件是什么,未知条件是什么,已知条件和未知条件的关系是什么……学生在教师的引导下说数学问题、说算式。在学生掌握了应用描述数学问题模型的方法以后,教师为学生出示其它的图片,学生需要通过迁移学习的方法来完成数学问题的描述。
以往,学生常常应用文学语言来描述事物,这种描述方式与数学语言描述存在差异。教师需要引导学生明白,不能应用过多的修辞语言来描述数学问题,即学生不用描述与数学问题无关的事物信息,更不能够在描述事物时模糊数量关系。学生需要应用一套科学的逻辑说明生活中事物的已知条件数量、未知答案的数量,然后能够应用数学逻辑建立它们之间的关联。
二、应用科学思维辅助数学语言表达
在描述一件事物时,学生需要学会应用科学的思维来说明这件事物的概念、性质、特点等。而如果没有科学的思维方法,学生是难以准确地完成数学问题的描述的。在引导学生应用数学语言描述问题的时候,学生需要先应用科学思维完成问题的描述,令事物的描述精炼、准确、有逻辑[2]。现以《角的认识》教学为例。
(一)说概述
数学概念的描述,是学生学习数学语言的重点。学生在探讨数学问题时,需要基于抽象化的概念作为依据来进行探讨,而不是基于某一个具象化的事物形象来进行探讨。假设学生的数学概念学习存在思维漏洞,那么他们在探讨问题的过程会存在各种问题。教师需要引导学生观看一个具象化的案例,这个案例能够呈现典型的数学概念,然后引导学生进行实践操作,以此强化学生的学习体验,让学生可以基于体验来理解概念。在学生认识了概念的基础上,教师需要引导学生思考概念形成的条件,以及条件与条件的逻辑关系。当学生能够应用科学的逻辑来说明概念以后,就意味着他们可以基于科学思维来认知数学概念。
教师给出几则案例,让学生判断案例中几个三角形的三个角分别是什么样的角?学生开始用量角器来量出角的度数。学生经过测量后,提出一个三角形的内角分别为一个“直角”和两个“锐角”。在这一环节,教师引导学生体验学习,在学习过程中掌握数学技能。接下来,教师引导学生说判断依据。学生在分析判断过程中,需要思考什么样的角是“直角”,什么样的角是“锐角”,在描述和思考的过程中形成概念。在完成概念学习后,教师需要引导学生举出生活中常见的“直角”与“锐角”的例子,共同分析生活中的“角”与几何图形中的“角”之间的差异,然后形成几何图形概念。通过这一则案例学习,学生从一则具象化的案例中理解了抽象化的“直角”与“锐角”的概念。
(二)讲思辨
小学生的抽象思维不足,他们在分析和解决问题的过程中会存在各种思维漏洞。教师需要引导学生学习典型的案例,然后应用数学语言来辨析命题。在说明自己思辨命题的过程中,他们会发现存在的思维漏洞,然后学生通过学习和交流,能够提升自己的思维水平,从而提高知识认知的水平。不同层次的学生思辨水平存在差异。在引导学生思辨数学问题时,教师需要了解学生层次的差异,然后通过优化教学组织,让学生形成思维互补。
在教学中,教师让学生以小组为单位,分工合作完成数学问题判断,学生在交流和探讨数学问题结果的时候,形成思维互补。教师引导学生分析案例中几个正方形图形分割以后三角形的数量与分类判断的问题,学生需要结合学到的知识分析角可以怎么分类?分类的范围是什么?标准是什么?不同分类的角有什么特征?在教师的引导下,学生应用科学的思维一一完成辨析。学生思辨数学问题的过程,就是让学生应用科学的思维去认知,然后结合理论知识来分析和判断数学问题的过程。在思辨的过程中,学生能够发现自己的逻辑思维漏洞,继而能够学会应用严谨的科学思维来分析命题。
(三)成体系
学生完成理论知识以后,需要回顾学习过程。学生认知思维的内容为概念,学生完成这一阶段的描述即完成认知的学习,这是他们需要形成的理论体系;学生需要什么样的技能来提出、思考问题,这是学生需要形成的技能体系;学生需要结合问题解决的需求掌握问题判断逻辑、计算方法,这是问题体系。教师需要引导学生一边应用数学语言说明,一边应用可视化图形来呈现学生思维的过程,在完成了整个知识体系的描述以后,学生便能形成全面的数学知识体系。
学生把“角的认知”知识体系、技术能系、问题判断的体系都呈现在图1上。在这个内容的学习中,为了避免遗漏系统知识点,学生以小组为单位,边回顾,边应用思维导图绘制知识形成、技能学习、问题解决的全部思维过程。在合作学习环境下,图1呈现了小组成员关于“角的认识”这一知识体系的建立。
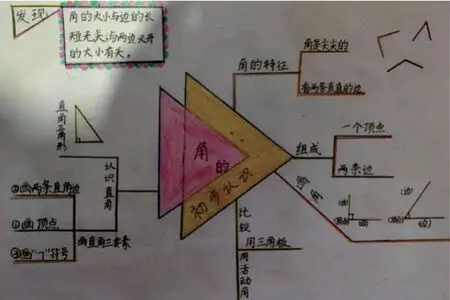
图1 “角的认知”体系图
三、应用数学语言表达剖析数学问题
在了解了数学语言表达的方式以后,学生需要学会应用数学语言来剖析数学问题。应用数学语言、数学公式、数学图形来分析数学问题,应用数学语言来理解数学问题,能让学生更加透彻地理解数学问题,而避免发生数学问题的歧义[3]。现以《百分比》的教学为例来说明。
(一)应用数学语言优化数学材料的梳理
有些数学问题,对于学生而言过于复杂,他们在应用数学语言梳理材料的时候会犯错误。他们需要通过学习把握数学材料分析的要点,从而才能理解数学语言到底描述了什么样的事物。抓住数学问题的描述,理解数学语言表达的意思,能够帮助学生审题,避免发生审题错误。
以学习百分数为例。学生用数学语言说百分比的应用题:“女生有30人,是男生的3倍,男女生一共有多少人?”有些学生没有认真地分析习题,就给出答案30+3=33,33+30=63,男生和女生总共有63人。此时,教师引导学生应用数学语言仔细分析数学材料,建立已经条件和未知答案。通过分析,学生发现探讨女生是男生的3倍,探讨的是把女生人数视为一个整体,然后男生人数为30÷3=10人,男女生一共有10+30=40人。通过这一次学习,学生意识到了在探讨人的个数与人的倍数存在不同的差异。如果探讨的是多3人,那么就要探讨人数+3,探讨的是多3倍,就是探讨人数×4。而如果应用题中男生人数是女生人数的120%,那男生人数就是女生人数×120%。学生在应用数学语言探讨问题时,必须了解问题探讨的对象、另一个对象和这个对象之间的关系、它们之间的数学关联。如果学生没有准确地把握数学问题的这三要素,就不能基于数学语言全面地梳理数学材料中的数量关系。
(二)结合问题本质理解数学语言表达
部分数学问题看似比较复杂,学生对应着数学语言难以理解它要表达的意思,教师就需要引导学生应用画表格、画图形等方式,让学生学会应用图形来呈现数学语言、用数据来分析数学语言中的数量关系。应用这样的方式,学生能够看到数学语言背后的本质,从而理解这个具象化情境中指向的问题。
例如,学生看到这样一题(如图2):大圆周长是小圆周长的n(n>1)倍。现小圆沿着大圆滚动一周,大圆滚动的圈数是小圆滚动圈数的几分之几?部分学生初看到这个数学问题,会觉得这个问题很难。那么现在,学生在图形上分析这个问题:现在小圆沿着大圆滚动一周,那么就意味着大圈有多长,小圆无论滚多少圈,最终它的长度会和大圆的圈数一样长。而题目给的已知条件是大圆周长是小圆周长的n倍,那么小圆沿大圆转一圈就意味着小圆转了n圈。结合图2显示的已知条件可知大圆滚动的圈数是小圆滚动圈数的几分之几,就意味着小圆长度÷大圆长度×100%。通过这一次的学习,证明有些数学信息难以从文字上直接看出,运用画图、绘表格等方法整理数学材料中的数量关系,就能比较容易地找到数学问题的已知条件、未知答案、数学问题关系的理论知识指向。
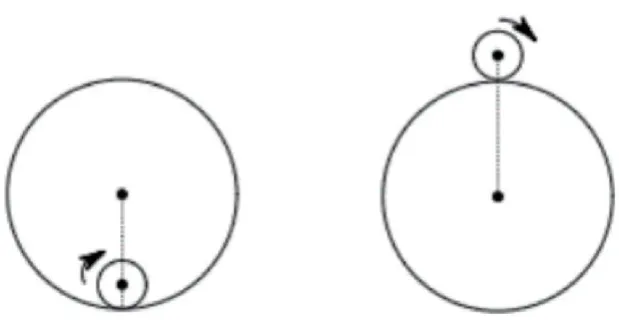
图2 大小圆具象化情境感知数量关系
四、总结
数学语言教学,是数学教学的重要内容。学生是否能够理解和诠释数学语言,决定着学生是不是能够应用数学思维来理解问题。受到环境的制约,很多乡村学生在小学时期没有夯实数学语言基础,于是教师需要重视数学语言教学。教师在开展数学语言教学时,要帮助学生打下说数学语言的基础,让学生能够从提炼数学材料的数量及建立数学材料关系的层面来进行学习;教师要引导学生从理解、辨析数学概念及建立数学知识体系的角度来掌握数学语言背后呈现的数学思维;教师要能从应用的角度熟悉数学语言表达方法及它的理论指向。

