淤地坝对黄土浅层滑坡的减蚀作用

张 霞， 于国强， 李 鹏， 李占斌

(1.西安理工大学省部共建西北旱区生态水利国家重点实验室，西安 710048；2.中国地质调查局干旱-半干旱区地下水与生态重点实验室，西安 710054)

黄土高原作为黄河流域的主要组成部分，是全球土壤侵蚀最为剧烈的地区之一，也是我国水土流失治理强度最高的地区。过去70年来，植树种草、淤地坝、梯田等水土保持措施的大规模推进，有效控制了土壤侵蚀，区域生态环境走向良性循环。新形势下，整个流域的侵蚀环境和侵蚀格局正在发生改变，遇极端强降雨天气，会滋生出如边坡崩塌、滑塌、坡面泥流以及淤地坝溃坝等一系列新的问题，情况更为复杂，侵蚀强度急剧增加，导致了新一轮严重的水土流失。如2013年陕北延安“7·23”特大暴雨洪灾、甘肃天水“7·25”群发性地质灾害、2017年陕北子洲“7·26”特大暴雨洪灾。在3次特大暴雨中，均发生了严重的坡面浅层滑坡，侵蚀剧烈、威胁巨大。

长期的水土保持实践经验证明，淤地坝作为主要的沟壑整治工程措施，在遏制黄土高原水土流失和减少入黄泥沙方面发挥了巨大作用。淤地坝不仅具有拦沙淤地的功能，更重要的是具有削峰减能，固沟减蚀的功效。淤地坝通过抬高侵蚀基准面，降低沟道比降，对泥沙输移起到了缓冲作用，改变了水-沙-能量的传输途径，降低了侵蚀能量，终止了沟头溯源侵蚀，防止沟道下切和沟岸扩张。由于缺少有效的数据和计算模型的支撑，研究还稍显薄弱，缺乏系统性；尤其是在极端强降雨条件下，基于侵蚀能量角度，关于淤地坝抬升对沟道发生浅层滑坡的减蚀作用的研究并不多见。因此，开展强降雨条件下，淤地坝淤积对浅层滑坡的侵蚀能量减蚀作用的研究具有十分重要的意义。

1 材料与方法

1.1 试验设计与模型几何结构

本研究对黄土高原丘陵区典型流域韭园沟流域的地貌特征进行勘测与统计，并对流域山脊线和山谷线进行提取和垂直距离测量，发现流域内梁峁坡坡度多为0～30°，沟谷坡坡度多为35°～45°，梁峁坡面积与沟谷坡面积比例分别占57%和43%；典型坡面的投影长度均值为105 m。据此对多发生浅层滑坡的沟谷坡地形进行概化，沿滑坡方向切出来的1个沟坡，该沟谷坡坡长60 m，坡度40°，坡高38.6 m，坡面宽30 m。

本研究结合实际沟谷坡高度，共设计无淤地坝(淤高0 m)、淤高5 m、淤高10 m、淤高15 m、淤高20 m、淤高25 m、淤高30 m，7种坝地淤高情况。通过对子洲“7·26”暴雨所发生滑坡的形态特征、规模和发生位置的调查和统计，将滑坡初始状态物质设定为球冠形状，该球冠高2 m，球冠最大开口圆的半径为1.5 m，位于沟谷坡顶部。按照上述沟谷坡几何形态、淤地坝淤高和滑坡初始状态，构建了沟谷坡滑坡数值模型试验，采取黄土流变模型开展数值模拟，以此来定量评估浅层滑坡运动以及动力、能量演进过程。

该模型几何结构设计为一个倾斜的坡面，代表沟谷坡，坡度为40°，(图1)。初始状态(淤高0 m)下，坡脚出口直接与沟底河道相连接，滑坡初始物质质心在-直角坐标系投影为坐标原点，轴方向为滑坡运动方向，垂直于河道(方向)。淤地坝位于沟底河道，在不同淤高状态下，出口边界位置均一致(=55)。初始、过渡状态(淤高10 m)和最终淤积状态(淤高30 m)的地形(图1和图2)。所有情况的物源初始条件、边界均一致。

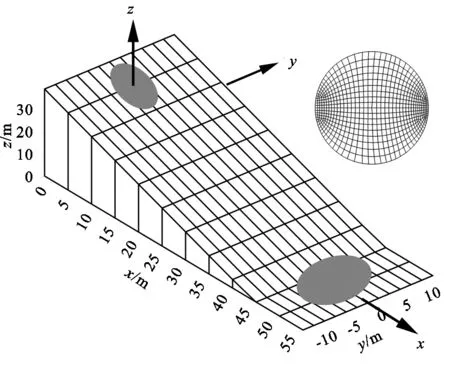
图1 数值模型试验结构示意

图2 数值模拟试验2种淤积状态

整个沟谷坡在轴方向宽为30 m(:-15～+15)，在轴方向长57 m(：-2～+55 m)，均为固定边界。无淤地坝时其水平区域长11.04 m(：+43.96～+55 m)，随坝地逐渐淤高，水平区域长度逐渐增大。假定滑坡物源区呈球冠状，在水平面投影的圆半径为=1.5 m，球冠高=2 m，该物源体积为7.715 m。滑坡经过沟谷坡运动到沟底(水平面)或坝体表面上。

1.2 动力分析模型选取

目前较为普遍的滑坡动力分析模型包括连续介质模型和质量集中模型。由于质量集中模型是将滑体重心和形心简化为一点，因此未能考虑滑体形变和不同部位的流速变化差异，这显然不能很好地刻画滑体的实际运动情况；另外该模型只能将下垫面简化为光滑壁面，不能真实反映地形起伏形态，因而未能计算流速和能量损耗的响应关系，存在局限性。而连续介质模型能够克服质量集中模型的不足，较为真实地反映出滑坡的运动过程和变形特征。因此，本研究采用连续介质模型对滑坡进行运动模型计算。

该模型假定滑坡在运动过程中，颗粒之间紧密连接且一起运动。在平面直角坐标系定义运动方向，方向向下为重力方向。将滑坡块体在水平投影的面积和垂直方向体积视为时间的函数。在拉格朗日参考系下，对滑坡运动轨迹进行计算，物质运动过程均遵循质量、动量和能量守恒。

1.3 流变模型和参数的选取

运动的滑坡为非牛顿流体，因此在物质运动过程中的不同高度会产生速度差，从而导致摩擦而出现剪应力。研究学者采用物质形变产生的剪应力和剪切率的关系来表征运动物质的流变特性，通常选用Friction模型、Bingham模型和Voellmy模型来计算流变特性。Voellmy模型已经广泛成功应用于颗粒流和泥石流的数值模型中；在子洲滑坡的实际情况下，由于滑坡在下坡的运动过程中，颗粒的高流动性会产生很强的湍流效应，这就需要在Voellmy流变模型中考虑；而且笔者前期采用Voellmy流变模型对黄土浅层滑坡进行了实例验证，取得了较好的模拟效果。本研究选取Voellmy流变模型开展数值模型计算，模拟黄土区滑坡的运动过程，包括运动物质的摩擦和湍流行为，其表达式为：

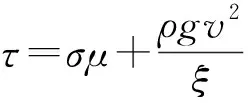
(1)

式中：为动力摩擦系数，=(1-)tan，本研究中将孔隙水压力比率引入模型中，用来计算孔隙水压的影响；为湍流(紊流)系数。

滑坡的流变特性取决于滑坡体物质的材料特性，其参数选取将直接影响最终的模型计算结果。本研究以子洲滑坡为原型，根据岩性成分分析和力学参数试验结果，最终确定了子洲地区滑坡的各流变模型参数：=01,=1 000 m/s。

本研究使用有限元求解法结合三维连续介质动态数值模型，编码Voellmy流变模型，对子洲强降雨诱发滑坡的运动轨迹距离、滑坡速度、能量进行模拟计算。

1.4 侵蚀率计算与选取

滑坡动力过程中常会伴有侵蚀现象的发生，极其重要却又是难点。鉴于实际情况复杂和土壤理化形式不均一性，其侵蚀速率仅能通过事件发生后的反分析确定。结合实际调研和工程实践，用相关准则进行简化：

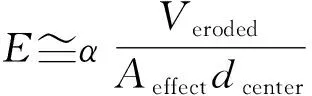
(2)

式中：是总侵蚀物质体积(m)；为侵蚀面积(m)；为运动物体中心的移动距离(m)，均通过实地测量估算。受系统非线性因素制约，修正系数()受实际下垫面地形和流变模型制约。笔者通过对多个滑坡的反复演算，计算修正系数()；对于Voellmy模型，由于湍流效应导致的非线性更强，本研究采用=2.2。

2 结果与分析

2.1 运动过程模拟

图3展示了淤地坝不同淤积高度下，滑坡在水平面内的运动轨迹和物质堆积情况。其中虚线为滑坡运动过程中不同时刻的轮廓线，时间间隔为1.0 s；竖线代表淤地坝与沟谷坡交界位置，等值线云图表示滑坡体最终堆积深度分布状态。从图3可以看出，在不同淤积高度下，滑坡的运动规律基本类似。滑坡发生时，均是沿着沟谷坡向沟底加速下滑，滑坡初始物质形状为圆形，其物质轮廓沿沟谷坡拉长，渐渐形成蝌蚪状，但在沟谷坡范围内的横向扩展很小。当进入坝体表面时，滑坡纵向扩展加剧，延伸十分明显，这与文献[14-16]记载的结果十分相似。同时不难发现，堆积区中心并未与最大深度位置重合，稍微有些靠前，反映了滑坡的前缘比中心具有更大的研究意义。

从堆积区厚度云图(图3)还可以发现，滑坡沿沟谷坡下降，尽管有物质不断被卷入，其运动物质的深度依然在不断减少。当运动停止，开始在沟底或淤地坝位体表面沉积，其物质体积逐渐增加，深度增大，最终成为了主体较厚、前缘较薄的扇形形态；直至停留在沟底或淤地坝位体表面，基本成扇形分布，且滑坡后缘依然有少部分停留于沟谷坡上。不同淤积状态下，堆积区最大深度均位于水平面(坝体)位置附近。随着淤地坝逐渐淤高，侵蚀基准面逐渐抬升，使侵蚀动能逐渐降低，滑坡最大移动距离大幅度减小，由没有淤地坝时的52 m减少至淤地坝淤高30 m时的16 m；滑坡堆积区深度也逐渐降低，由初始状态的0.5 m降低至最终状态的0.2 m；堆积区范围也逐渐减少，纵向范围由初始状态的20 m减少至最终状态的10 m。

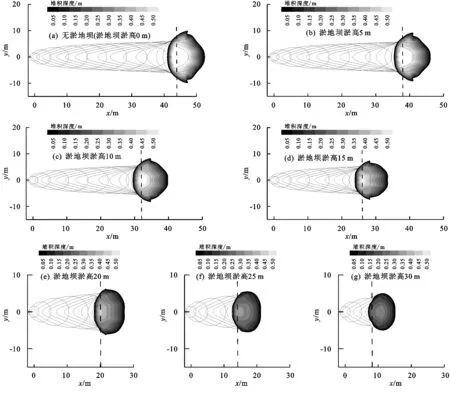
图3 滑坡运动模拟结果

2.2 动力过程模拟

在上述滑坡运动过程分析基础之上，继续对淤地坝不同淤积高度下的滑坡动力参数(平均速度、前缘速度、总势能、总动能)、滑坡体面积以及体积随时间的变化情况进行汇总。由图4和图5可知，在淤地坝不同淤积高度下，滑坡在运动过程中，各动力参数和侵蚀面积的曲线形态基本一致。滑体在沟谷坡运动过程中，其平均速度(滑坡体在运动过程的每个时刻下，作为一个整体的速度，即各个单元的速度求平均所得)、前缘速度、总动能均呈急剧增加态势；在进入水平面和坝体表面后，均呈下降趋势(图4)。亦可以看出，滑坡体前缘在触碰坡脚时，其前缘速度并未立刻减少，由于惯性作用出现了一个缓慢增加的趋势，其速度最高可达9.52 m/s，然后开始下降。总势能的变化趋势同其他3个参数的变化过程不一致，仅在没有淤地坝的情况下，出现了先增加再降低的过程，此结果与前期采用此模型计算天水“7·25”娘娘坝黄土浅层滑坡动力过程相似，这也在一定程度上也验证了本次模拟结果的准确性。在其他状态下，随着淤积高度的逐渐抬升，势能呈现增加态势，但受侵蚀物质质量和高度因素的影响，规律不是十分明显。

从滑坡体体积随时间的变化情况可以看出(图5b)，当滑坡在沟谷坡运动过程中，由于侵蚀作用的存在，能够卷积许多下垫面物质，使得滑坡体体积逐渐增大，没有淤地坝时，滑坡体体积由最初的7.7 m增加到最终的56.5 m，增加近7倍。总体来说，当滑坡运动至水平面时，由于速度急剧增加，滑坡体体积快速增加，导致侵蚀能量急剧增加(图4d)，这解释了坡脚处侵蚀较为严重的原因，同时也解释了图4b中滑坡前缘速度出现波动的原因，这与前人的研究结果相类似。在滑坡侵蚀过程中，由于运动物质在能量传递过程中出现了损耗，使得整体速度减慢。

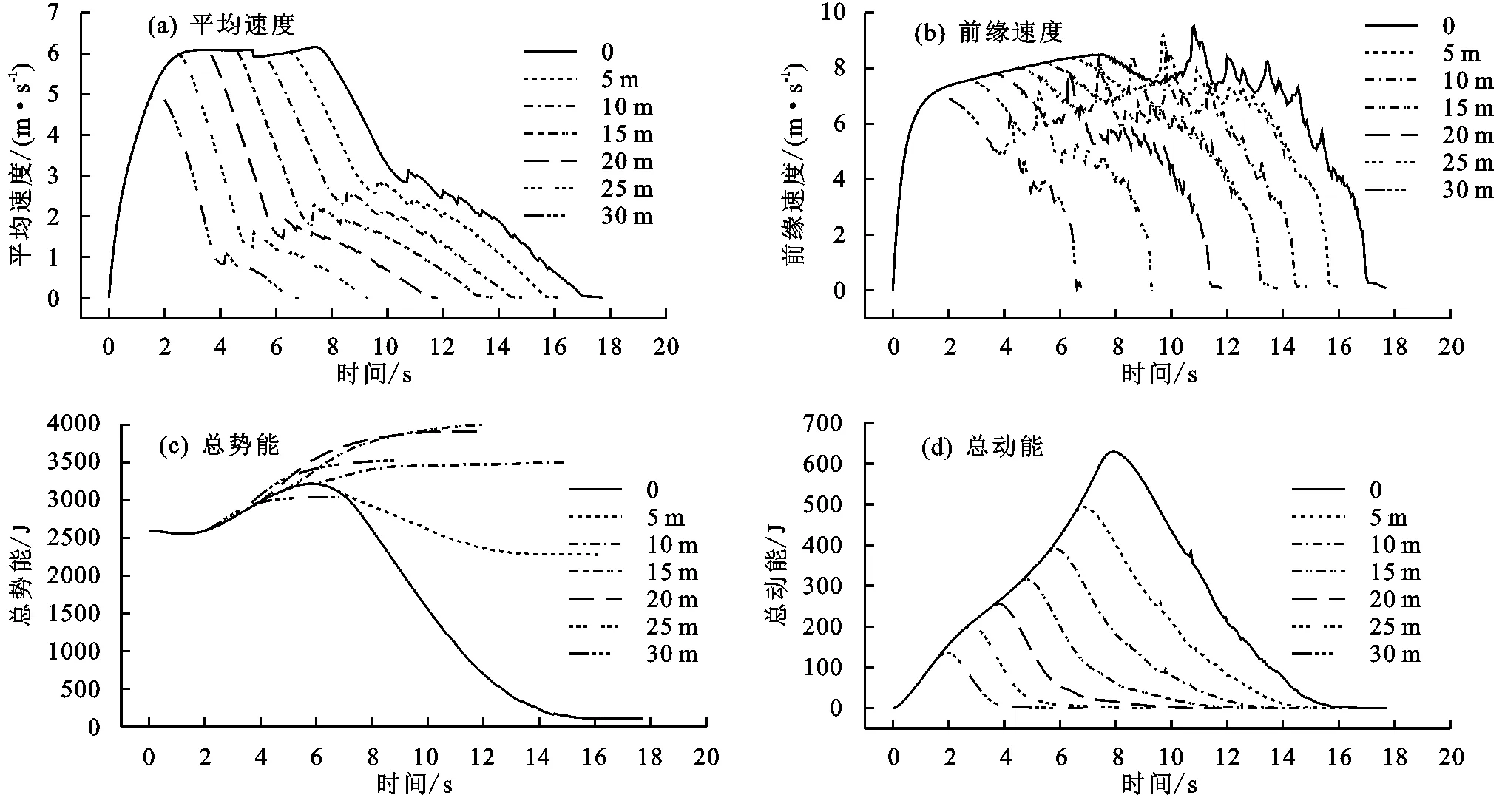
图4 滑坡动力参数模拟结果

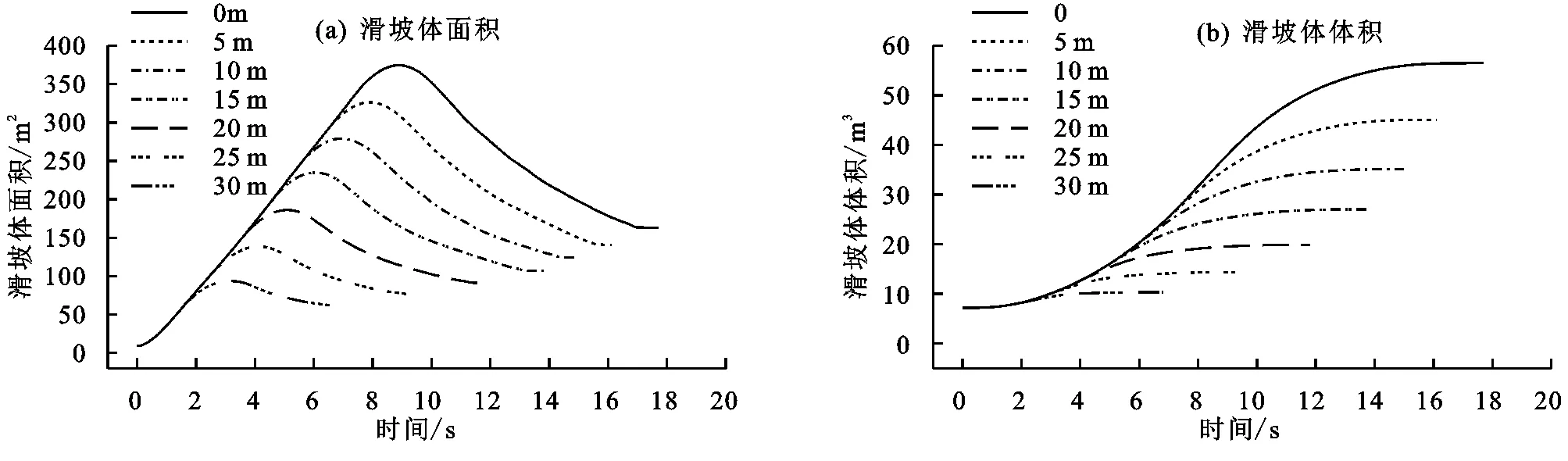
图5 滑坡体面积、侵蚀物质体积模拟

2.3 侵蚀动力对淤地坝淤积的响应

为研究淤地坝淤积对各个运动参数的影响作用，对淤地坝不同淤积高度下滑坡体的运行时间、移动距离、侵蚀体积、动力参数和能量参数进行函数拟合。由图6可知，各个指标拟合函数的判定系数()均在0.99以上，其拟合精度较高，可用于淤地坝减蚀作用的定性分析与定量计算。不难发现，随着淤地坝淤积高度的逐渐升高，侵蚀基准面逐渐抬升，滑坡的各项指标均有不同程度的下降。其中运行时间、平均速度峰值呈Sigmoidal函数下降趋势，前缘速度和滑坡移动距离呈线性函数下降趋势，侵蚀物质体积和总动能呈指数函数下降趋势。

当淤地坝淤高至30 m时，运行时间、平均速度峰值、前缘速度、移动距离、侵蚀物质体积和总动能分别减少10.9 s，1.15 m/s，2.39 m/s，37.5 m，46.18 m，4 145 J，降幅分别为61.58%，18.69%，25.13%，71.43%，81.73%，93.95%。从降幅可以看出，当淤地坝淤积高度从0抬升至30 m时，其速度参数(平均速度峰值、前缘速度)相比较其他指标而言，其降幅不是很大，仅为18.69%和25.13%，这点也可以从图4中得到印证。在滑坡体未在接触坝体表面前，其运动速度一致；在接触淤地坝后，其平均速度峰值变化不大，仅是运行时间缩短(图4a)；尤其在淤地坝淤积高度<20 m时，平均速度下降幅度则更小(图6b)。这说明淤地坝的淤积高度对滑坡速度影响较小，仅在一定程度上抑制了速度的增加，而且当淤地坝淤积一定高度后减速效果才明显。

图6 滑坡指标随淤积高度变化规律

3 讨 论

从平均速度、前缘速度和总动能的曲线趋势(图4)可以看出，滑坡体前缘在未接触淤地坝坝体时，各个动力参数变化规律一致；在接触淤地坝之后，随着淤地坝逐渐淤高，3个参数的峰值都在逐渐减小，且整个运动过程都在缩短，呈现“压缩”状态。总之，随着淤地坝逐渐淤高，滑坡停止得越快，各项动力参数逐渐减少。说明随着侵蚀基准面的抬升，淤地坝除了对整个坡体的稳定性有提升作用外，还对各个侵蚀动力参数均有不同程度的影响。同时，由于滑坡的侵蚀效应在运动过程中十分重要，可使得滑坡体质量急剧增大，同时也具备较大的运动速度，破坏性进一步增强；这也解释了滑坡体初始方量虽然不大，最终破坏力较强的原因，这一结论与前人的研究成果一致。

相比滑坡的各个速度参数指标，淤地坝对其他动力指标的影响作用则比较显著。当淤地坝淤积高度从0抬升至30 m时，其他指标降幅达到61.58%～93.95%，降幅效果非常明显。分析原因可知，首先淤地坝通过逐渐淤高，逐渐缩短了滑坡运行时间，减少了滑坡在沟谷坡上的运行距离，逐渐限制了滑坡体的运动空间。这样不但可以在一定程度上限制了速度的快速增长，更重要的是减少了滑坡侵蚀空间，有效抑制了滑坡体的侵蚀作用，使得侵蚀物质体积大幅降低，降幅最高可达81.73%，从而进一步大幅减少了侵蚀物质质量。最终在滑坡体速度和侵蚀物质质量减少的双重作用下，导致滑坡体的侵蚀总动能急剧减少，降幅最高可达93.95%。结果与前人采用拦挡坝计算滑坡运动时的结果也十分相似，从降低侵蚀能量和动力参数的角度验证了淤地坝具有固沟减蚀、降低侵蚀能量，终止沟头溯源侵蚀的功效。

综合以上分析可知，随着淤地坝逐渐淤高，侵蚀基准面逐渐抬升，减少了滑坡的运动空间和侵蚀空间，仅在一定程度上降低了滑坡速度，但却有效抑制了滑坡的侵蚀作用，降低了侵蚀物质质量，从而有效减少了滑坡体侵蚀总动能，降低了滑坡体移动距离。因此，侵蚀基准面逐渐抬升，可以在很大程度上减少滑坡的致灾强度和致灾规模。

4 结 论

(1)浅层滑坡在沟谷坡运动过程中，其平均速度和前缘速度急剧增加。由于滑坡的侵蚀作用导致运动物质质量和侵蚀总动能急剧增大，加之较大的运动速度，极具破坏性。滑坡运动至坝体表面时，滑坡体体积和侵蚀能量急剧增加，导致了滑坡前缘速度出现波动和坡脚处的严重侵蚀。滑坡运动至淤地坝坝体表面后，各动力指标、滑坡堆积区深度、纵向范围均有不同程度下降。

(2)随着侵蚀基准面抬升，浅层滑坡运行时间、平均速度峰值呈Sigmoidal函数下降趋势，前缘速度和滑坡移动距离呈线性函数下降趋势，侵蚀物质体积和总动能呈指数函数下降趋势。拟合函数精度较高，可应用于淤地坝减蚀作用的定性分析和定量计算。

(3)随着淤地坝逐渐淤高，侵蚀基准面逐渐抬升，减少滑坡的运动空间和侵蚀空间，仅在一定程度上降低滑坡速度，但却有效抑制了滑坡的侵蚀作用，大幅降低了侵蚀物质质量，从而有效减少了滑坡体侵蚀总动能，使得滑坡体移动距离急剧下降，可以在很大程度上减轻浅层滑坡的致灾强度和致灾规模。