布尔环及其谱的一些性质

郭俊辉

(广州大学 数学与信息科学学院, 广东 广州 510006)

布尔环的出现是由布尔代数作为背景衍生出来的，布尔代数在代数学(代数结构)、逻辑演算、集合论、拓扑空间理论、测度论、概率论和泛函分析等数学分支中均有应用，1967年后, 在数理逻辑的分支之一的公理化集合论以及模型论的理论研究中, 也起着一定的作用。近几十年来, 布尔代数在自动化技术、电子计算机的逻辑设计等工程技术领域中有重要的应用。布尔代数一词源于英国数学家Boole,他把逻辑简化成极为容易和简单的一种代数。在这种代数中, 适当材料上的“推理”, 成了公式初等运算的事情。例如矛盾律, 即A不能既是B又是非B, 它可表示为x(1-x)=0; 排中律可被说成x+(1-x)=1。“且”对“或”的分配律可以表示为x(u+v)=xu+xv。 这样, 就使逻辑本身受到数学的支配[1]。为了使自己的研究工作趋于完善, 布尔在此后的漫长时间里, 又付出了不同寻常的努力。1854年, 他发表了《思维规律》这部杰作,布尔代数问世了。后来, Ernst较为系统地给出布尔代数和分配格的定义[2]。在离散数学中, 布尔代数(有时叫布尔格)是有补分配格。首先提出布尔环与布尔格之间的紧密联系的是Stone。在数学中, 斯通氏布尔代数表示定理声称所有布尔代数都同构于集合域。这个定理是深入理解在20世纪上半叶所拓展的布尔代数的基础，该定理首先由斯通1936年证明, 并以他的姓氏命名。斯通通过对希尔伯特空间上算子谱理论的研究而得出了它。这个定理有多种阐述语言, 例如任意一个布尔代数一定同构于某个集上的一个集合域, 又或者说任意一个布尔代数也一定同构于某个拓扑空间的闭开代数等, 也可以用拓扑学和范畴论的语言来重述如下: 斯通表示定理断言在布尔代数范畴和斯通氏空间, 也就是完全不连通紧致Hausdorff拓扑空间(也叫做布尔空间)范畴之间的对偶。在本文中,作者试图要将斯通定理叙述为更为简单浅显的一个版本, 即: 任意一个布尔格都与某个紧致的Hausdorff空间中的全体既开又闭的子集合所组成的格同构。在本文的第一部分通过对这个定理的推理,发现了布尔环及其素谱空间的特殊性, 它有着其他一般交换环及对应素谱不一定有的性质。本文在第二部分正是利用了布尔环的特殊性质推广了一个在一般交换环上成立的命题: 有限个素理若想可以覆盖一个理想, 则必有其中一个素理想覆盖住该理想。在布尔环中, 借助谱的知识, 该命题中的条件“有限个”在某种条件下可以去掉。在文章的末尾, 则单独探究布尔环谱空间的拓扑性质, 除了发现这种空间是“散碎的”、完全不连通的, 还发现当将谱空间的经典拓扑(Zariski拓扑)划分得更细, 划成可构造拓扑时, 两种情况实际上是一回事, 即根本没有变得“更细”。

1 斯通定理

斯通表示定理在数学史上影响深远, 正如上文所说, 斯通定理在不同的场合下表达出来的语言也是不一样的, 又例如这样的表达: 任一布尔代数同构于其全体极大滤子构成的紧致零维 Hausdorff空间中的开闭集代数。受斯通定理的思维火花影响, 不少学者继而不断揭示偏序集与拓扑空间之间的关系[3-5]。随着研究的加深, 近年来多值逻辑也有较快的发展[6-7], 而一些具有蕴含性质的格, 例如R0-代数、BL-代数、MTL-代数等也相继被提出。自然地, 一些斯通定理的推广工作也相继进行着, 如在R0-代数上推广了布尔代数的斯通定理[8-9]。也有一些学者, 例如刘应明等[5]对某类完全分配格给出了斯通定理的格值形式, 用范畴的语言说, 即分配格范畴对偶同构于凝聚L-locale范畴, (前提是)若格L是一个frame且0∈L是素元或1∈L是余素元。更进一步, 假若L还是完全分配的, 则分配格范畴对偶同构于凝聚满层L-拓扑空间范畴。由以上叙述可感知斯通定理至今还不断焕发着它的活力, 归根结底是因为斯通表示定理揭示了格论与拓扑空间理论之间的深刻联系, 而王国俊[10]更是有创意地将斯通表示定理与广义空间理论以及拓扑分子格理论这些新学科联系起来研究。同样让人印象深刻的是郭铁信等[11]于2011年在复完备随机内积模上的随机酉算子群上面建立了斯通表示定理。在国外的一些研究中, 有不少学者把注意力投向了布尔超代数, 先是Procesi等在文献[12]中证明了布尔超代数上的斯通表示定理, 后来Procesi在文献[13]中用拓扑的角度看待问题, 并用拓扑语言阐述了布尔超代数上的斯通表示定理。

本文中提到的布尔环是所有元素都满足x2=x的含幺交换环。以下首先介绍有关格的概念。格是一种特殊的偏序集, 经过特殊化以后得到分配格, 再特殊化以后可以得到布尔代数, 是序结构的主体部分。在许多数学对象中, 所考虑的元素之间具有某种顺序。例如一组实数间的大小顺序, 一组命题间的蕴涵顺序等。这种顺序一般不是全序, 即不是任意2个元素之间都能排列顺序, 而是在部分元素之间的一种顺序, 称为偏序。偏序集和格就是研究顺序的性质及作用而产生的概念和理论。格是其非空有限子集都有一个上确界和一个下确界的偏序集合。在19世纪的后几十年, 德国数学家戴德金和施履德分别从数论和逻辑代数两个方向得出格的概念。但是其他数学家并未认识到它的重要性。直至20世纪30年代, 在美国数学家伯克霍夫和挪威数学家奥尔的共同努力下, 格论才焕发生机, 发展成为一门独立的数学学科, 在抽象代数、射影几何、点集论、拓扑学、泛函分析、逻辑和概率论等诸多领域产生广泛应用。例如在代数学中对于一个群与其子群格之间关系的研究, 在数理逻辑中关于不可解度的研究。在图论中关于图分解的研究也大量用到格论。在密码学领域, 关于公钥密码分析学的应用研究也常用到格理论及格基约减算法。

首先需要谈及格的定义, 它有2种定义, 一种是代数定义, 另一种是偏序定义, 2种定义相互等价且在谈论格的时候永远不要将2种定义割裂来看。

定义1[14](格的代数定义) 设L为一个集合, 在L上定义2种在L中封闭的运算∨和∧, 使得对任意a,b∈L满足以下性质:

(1) 交换律a∨b=b∨a,a∧b=b∧a;

(2) 结合律a∨(b∨c)=(a∨b)∨c,a∧(b∧c)=(a∧b)∧c;

(3) 幂等律a∨a=a,a∧a=a;

(4) 吸收律a∨(a∧b)=a,a∧(a∨b)=a。

则称(L,∨,∧)是一个格。

定义2[14](格的偏序定义) 设L是一个偏序集, 且使得任意2个元素构成的子集{a,b}一定有上确界(最小上界)和下确界(最大上界), 则称(L,≤)是一个格。

以上2种定义是相互等价的, 有了定义1, 可定义偏序关系为a≤b当且仅当a∧b=a, 或者等价地说a∨b=b(容易验证这样定义的关系确实为偏序关系), 则有

inf{a,b}=a∧b,sup{a,b}=a∨b。

反之, 由定义2出发, 可分别定义2种运算为

a∨b=sup{a,b}和a∧b=inf{a,b}。

容易验证这样定义的运算∨和∧满足以上定义1中公理化要求的4个律[14]。自然地, 关于格同构也有2种相对应的等价叙述[14]: 格L1与L2同构是指能够建立L1到L2的一一映射φ使得映射φ可以保持2个运算∨和∧, 或者等价地说,φ和φ-1都是保序的, 其中，φ-1是保序的这一条件是不可省略的。

布尔格是一种特殊的格, 就好比布尔环是一种特殊的环。布尔格的定义则要在格的定义上再加多几个公理化要求。

定义3[15]设(L,∨,∧,≤)是一个格, 如果再有以下的性质被满足:

(1)L中有最大元和最小元(分别记作1和0);

(2)2个运算“∨”和“∧”都对另一个满足分配律, 即

(a∨b)∧c=(a∧c)∨(b∧c),

(a∧b)∨c=(a∨c)∧(b∨c);

(3)任意一个元a∈L, 存在唯一的补元a′∈L使得

a∨a′=1,a∧a′=0，

则称这种格是布尔格。

下面将指出布尔环和布尔格其实本质上是一回事, 两者互相诱导, 一一对应, 从而为后面阐明斯通定理做出铺垫准备。

引理1[15-16]布尔环和布尔格相互诱导, 一一对应。

现在介绍一些布尔环的性质, 以及交换环的素谱概念和布尔环的谱上性质。

引理2 交换环中若任意一个元素x∈A都有某个n∈且n>1, 使得xn=x, (n依赖于x), 则A中所有素理想都是极大理想。

x(1-xn-1)=0,

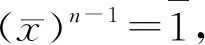
若n>2, 则

找到了逆元, 证毕。

命题1 在布尔环中有

(1)对一切x∈A,有2x=0;

(2)任意的素理想P都极大,且A/P是只有0与1的域;

(3)有限生成的理想是主理想。

证明

(1)这是较显然的;

(2)由引理2, 即可得；

(3)只需证明由2个元素生成的理想是主理想即可。现证明以下断言即可, 即

(x,y)=(x+y+xy)。

(x+y+xy)⊆(x,y)是显然的; 反过来, 由(1)的结论, 有

x(x+y+xy)=x,y(x+y+xy)=y，

故(x,y)⊆(x+y+xy), 断言成立。同理对3个元素的情况也有

(x,y,z)=(x+y+z+xy+xz+yz+xyz),

以此类推, 证毕。

以下简单提及交换环的素谱概念[15]。这是一个在代数几何中很基本的概念, 有的时候谈及环的局部化都会必不可少地谈及素谱。环的素谱和谱空间理论起源于仿射代数簇(又称代数流形)的研究。现已广泛应用于许多数学分支中, 如代数几何、层论、C*-代数、拓扑学、环论、模论、格论和群论等。几何性质和代数性质之间会相互反馈信息。每一个几何性质都会返回一个代数性质, 例如层(Sheaf), 那么反过来代数性质也能返回一个几何性质, 例如素谱, 合在一起就成了概型(Schemes)。素谱的概念在交换代数以及代数几何中扮演了一个很基础的角色, 就好比小学课本中的加减运算。素谱的可研究价值极大, 例如从范畴论的角度去看, 素谱还具备函子性: 素谱可以视作反变函子。更多性质细节可参考文献[15]。设A是一个交换环,X是它所有素理想的集合, 设E是A中的子集,α是E所生成的理想, 记

V(E)={P∈X|P⊇E},

则有以下性质:

(2)V(0)=X,V(1)=∅；

(3)设(Ei)i∈I是A中的一个子集簇, 那么V(∪i∈IEi)=∩i∈IV(Ei)；

(4)设α,β是A中任意2个理想, 则V(α)∪V(β)=V(α∩β)=V(αβ)。

从以上性质可以看出形如V(E)的全体所构成的集族满足闭集的拓扑公理, 于是X可以构成一个拓扑空间, 定义X中的闭集: 子集F为闭集当且仅当F可表成上述V(E)的形式。该拓扑空间(X,τ)叫环A的素谱(记为Spec(A)), 这个拓扑τ称为Zariski拓扑。

注记1 Zariski拓扑并不是人们在X上研究的唯一拓扑, 只是研究的最多的拓扑, 如无特别声明, 都是认为素谱上的拓扑是Zariski拓扑。另外比较多见的拓扑是可构造拓扑(记为τc), 在文章后面会提及关于布尔环在可构造拓扑下的素谱的相关性质特点。任意交换环在Zariski拓扑或者可构造拓扑下的素谱空间都是紧致的[15]。

注记2 对任意交换环A中的任意元素f, 定义

Xf=X[V((f))]={P∈X|f∉P},

则Xf显然是(X,τ)中的开集, 并且全体形如Xf的集族能构成(X,τ)的一组拓扑基[14]。且有以下性质:

(1)Xf∩Xg=Xfg；

(2)Xf=∅⟺f是幂零元；

(3)Xf=X⟺f是可逆元。

更详细的性质可参考文献[14]。

命题2[15-16]设A是布尔环, (X,τ)是带有Zariski拓扑的A的素谱空间, 则

(1)每一个Xf在(X,τ)中既开又闭；

(2)对有限个f1,…,fn∈A, 存在f0∈A, 使得Xf1∪…∪Xfn=Xf0；

(3)形如Xf的集合是(X,τ)中仅有的既开又闭的子集；

(4)(X,τ) 是紧致的Hausdorff空间。

证明(1)～(4)在文献[15-16]中都有涉及。这里简单提及(2), 要解决有限个的情形只要解决2个的情形即可, 结合命题1中的(3), 有

Xf∪Xg=[V((f))∩V((g))]c=

[V({f,g})]c=

[V((f+g+fg))]c=Xf+g+fg。

在本文的下一个部分由(4)会推出深刻的结论。

结合以上的铺垫得到最后的斯通定理:

定理1[3,15](斯通定理) 任意一个布尔格都与某个紧致的Hausdorff空间中的全体既开又闭的子集合所组成的格同构。

证明给出任意的一个布尔格(L,∨,∧,≤), 根据引理1, 设A是与之对应的布尔环, (X,τ)是环的谱, ∑={Xf|f∈A}, 则∑是紧致的Hausdorff空间(X,τ)中全体既开又闭的子集集合, 定义偏序关系为集合的包含关系, 即

Xf≤Xg⟺Xf⊆Xg,

这种情况下对应的运算“∨”和“∧”实际上就是集合的并和交，则容易验证(∑,∨,∧,≤)构成一个格。下面验证格同构(L,∨,∧,≤)≅(∑,∨,∧,≤)，定义映射：

φ:L→∑为φ(f)=Xf,

则根据引理1以及命题2可得:

φ(f∨g)=φ(f+g+fg)=Xf+g+fg=

Xf∨Xg=φ(f)∨φ(g)。

根据注记2中的性质(Xf∩Xg=Xfg), 有

φ(f∧g)=φ(fg)=Xfg=Xf∧Xg=φ(f)∧φ(g)。

通过验证,φ确实保持运算“∨”和“∧”, 因而是格同构, 从而完成了证明。

2 布尔环的素谱的一些性质

以上通过推理出斯通定理的一个简单形式，发现了布尔环的独特性, 并且这种独特性会转嫁到它的素谱中, 使得它的素谱也是一个很特别的拓扑空间。在这个部分,将特别研究布尔环的素谱的一些性质。

布尔环所具备的特殊性, 首先可以用来拓展一个在普通的交换环上很重要且经常使用但是又难以拓展的性质: 若存在有限个素理想可以覆盖一个普通的理想, 则必有其中一个素理想覆盖住该理想。为了阐明这项工作, 先做一些铺垫准备, 介绍一些相关知识。

命题3 任意的交换环的素谱(X,τ)中,Xg是紧致的子集(对任意的g∈A)。

证明只需证明假若一簇拓扑基中的成员{Xfi}i∈I能够覆盖住Xg, 则有有限的子覆盖即可。设Xg⊆∪i∈IXfi, 即有蕴含关系:P为A中的素理想,g∉P⟹∃f0使得f0∉P,

等价于

fi∈P,∀i⟹g∈P，

则有等式:

V({fi│i∈I})=V({g,fi|i∈I})。

于是有

得

这就存在有限个fi1,…fik以及某n∈使得

gn=c1fi1+…+cnfik,

则素理想P如果同时包含fi1,…fik, 则会包含gn, 从而包含g, 因而有

证毕。

定义4[17]拓扑空间中的子集族称为有核的, 如果中任意有限个成员之交非空。

命题4[17]拓扑空间(X,τ)紧致当且仅当X的任意有核闭集族之交∩A∈A≠∅。

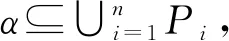
借助布尔环的特殊性,可对上面的问题做出其中一种回答, 具体的表述如下:

命题5 在布尔环A中, 设X是它的素谱, 设理想α⊆∪P∈XfP, 则必存在某P0∈Xf使得α⊆P0。

证明集族{V((a))∩Xf|a∈α}是紧致的子空间Xf上的闭集族, 并且是有核的, 事实上,

[V((a1))∩Xf]∩…∩[V((an))∩Xf]=

V((a1,…,an))∩Xf=V((a0))∩Xf,

其中，(a1,…,an)=(a0)是由命题1(3)得来, 且a0∈α, 由α⊆∪P∈XfP可知会存在某个P′∈Xf使得a0∈P′, 则

P′∈V((a0))∩Xf,

即集族{V((a))∩Xf|a∈α}是有核闭集族, 根据命题4, 集族{V((a))∩Xf|a∈α}全员之交非空, 则会存在一个P0∈Xf使得

P0a, ∀a∈α,

即

α⊆P0,

证毕。

注记3 以上命题条件中的Xf当然也可以换成某个V(E), 因为V(E)是紧致空间中的闭集, 从而也是紧致的[17], 然后用同样的方法去证明。

关于布尔环的素谱空间有一个很特别的拓扑性质, 就是完全不连通, 即任意一个至少含2点的子集都是不连通的, 也就是说连通的子集只能是单点集。由于布尔代数的影响很大且性质独特, 故和布尔代数相挂钩的研究对象也变得“特别”了, 例如现在讨论的布尔环的素谱空间。所以, 完全不连通的紧致的Hausdorff空间就被人们特别地称为“布尔空间”[3,14-15]。根据文献[18]的引理3.1，至少可以知道非平凡含幺布尔环的素谱空间一定是不连通的，但是仅仅得出这个结论还远远不够，所以有下面的命题6：

命题6 布尔环的素谱空间是布尔空间。

证明根据命题2(4), 只需证明(X,τ)中任意一个至少含2点的子集F都是不连通的即可。设

P1,P2∈F⊆X且P1≠P2,

则存在某个Xf使得P1∈Xf且P2∉Xf, 无疑Xf是开集, 但是它也是闭集, 根据命题3,Xf是紧致的子集, 在紧致的Hausdorff空间中紧致子集等价于闭集[17], 所以Xf既开又闭。故Xf∩F是F中既开又闭的真子集(含P1却不含P2), 所以F不连通。

注记1中提到的可构造拓扑τc, 一方面提及这种拓扑的一个原因是可构造拓扑本身也是交换环的素谱上的重要研究对象, 另一方面, 针对本文着重研究的布尔环, 它的素谱上的可构造拓扑有着一个有趣的事实: 布尔环的素谱带上Zariski拓扑和带上可构造拓扑其实是一回事。

先介绍什么是可构造拓扑。

定义5[15]对任意的交换环A, 记X为A的全体素理想的集合, 记

τc={U⊆X│存在交换环B以及环同态f:A→B,使得XU=f*(Spec(B))},

其中,f*:Spec(B)→Spec(A)定义为: 对任意的q∈Spec(B), 有

f*(q)=f-1(q)∈Spec(A),

τc能够构成一个拓扑从而使(X,τc)成为一个拓扑空间, 称τc为X上的可构造拓扑。

注记4 对以上τc的拓扑公理的验证, 只需验证闭集的拓扑公理即可[15]:

(1)设有一族交换环Bi以及相配的环同态fi:A→Bi,i∈I, 指标集I可以是无穷集, 则有

记指标集

∑={J|J⊂I,是I中的有限集},

定义∑中的序关系:

J≤K⟺J⊆K,

则∑是一个正向集 (即特殊的偏序集, 满足对任意的2个指标i,j都会存在某个指标k使得i≤k以及j≤k), 因为对任意的J,K∈∑有

J∪K∈∑,J⊆J∪K,K⊆J∪K,

对任意的指标J≤K, 有典范的A代数同态

μJK:BJ→BK,

则(BJ,μJK)构成一个正向系统[15]。最后定义无穷个A代数Bi的张量积为该正向系统的正向极限, 即

(i)设(Bi,gij)是一个环的正向系统,B是正向极限, 对每个i都有环同态fi:A→Bi, 且对任意的i≤j都有gij∘fi=fj(即(Bi,gij)构成A代数的正向系统)。fi自然诱导出f:A→B, 则有结论

(ii)设有环同态f:A→B以及g:A→C, 定义同态h:A→B⊗AC为

h(a)=f(a)⊗1,

则有结论:

h*(Spec(B⊗AC))=f*(Spec(B))∩g*(Spec(C))。

至此, 结合(i)与(ii)的结果就自然得到

(2)设有环同态:f1:A→B1以及f2:A→B2, 定义环同态:f:A→B1×B2为

f(a)=(f1(a),f2(a)),

则有

f*(Spec(B1×B2))=f1(Spec(B1))∪f2(Spec(B2))。

(3)对于零同态:f:A→0, 有f*(Spec(0))=∅。

(4)对于恒同映射id:A→A, 有(id)*(Spec(A))=X。

命题7 可构造拓扑比Zariski拓扑更大(或者说更细), 即τ⊆τc。

证明只需证明Zariski拓扑中的闭集一定是可构造拓扑中的闭集即可。任取Zariski拓扑中的一个闭集V(α), 其中α是任意一个A中的理想。有典范同态

π:A→A/α,

则有V(α)=π*(Spec(A/α)), 证毕。

命题8 可构造拓扑是使得交换环的素谱中Xf既开又闭的最小拓扑(任意的f∈A)。

证明(1) 首先证明Xf在可构造拓扑中既开又闭, 是开的已经显然了。记Af是A的分式环, 即其中的乘法封闭子集是f的所有次幂(含1=f0)所构成的集合, 则有典范同态

φ:A→Af,

则Xf=φ*(Spec(Af))。从而Xf也是闭集。

(2)设τΩ是定义在X上的使得任意Xf既开又闭的拓扑, 需要证明

τc⊆τΩ,

即需要证明对任意的ψ:A→B,ψ*(Spec(B))是(X,τΩ)中的闭集。

设

P1∉ψ*(Spec(B)),

则P1因为有P是B中的一个素理想的局限当且仅当P=Pec这一等价条件[15]。取f∉P1且则设

其中，gi∈P1,bi∈B。则

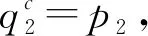
因此

这与P2∈Xf相矛盾。综上可得ψ*(Spec(B))是(X,τΩ)中的闭集。

有了以上的铺垫工作, 现在可以说在布尔环上的Zariski拓扑和可构造拓扑是一回事。由命题2知道布尔环上的Zariski拓扑是使得每一个Xf既开又闭的拓扑, 所以由命题8可知τc⊆τ, 又由命题7得τ⊆τc, 综上可得这2种拓扑实际上是一回事。