基于LCSS算法的膝、踝关节相似性特征研究*

刘 旭，尹雨晴，赵雪冬，代雪晶，汤澄清

（中国刑事警察学院，沈阳 110000）

0 引言

刑事科学技术中，人身识别的技术包括指纹识别、虹膜识别、笔迹识别、声纹识别、人像识别、DNA 识别、步态识别等[1]。其中人像识别[2]、虹膜识别[3]、步态识别可以实现非接触远距离的识别。但是随着疫情防控常态化人们防护意识的提升，戴口罩的情况不可避免的会影响到人脸识别的应用性。而步态识别相对于虹膜识别来说不但可以实现远距离识别而且也不便于伪装，步态识别作为近些年新兴的研究领域，在足迹检验技术、视频犯罪侦查、医疗诊断及康复、计算机视觉等领域中获得了越来越多的关注和重视。

早在1994 年来自MIT 媒体实验室的Niyogi 与Adelson[4]就开始对人进行步态识别。国内在2003 年，王亮等[5]提出了一种简单有效的自动步态识别算法。同年，郭忠武等[6]将行走中的下肢关节角度作为分类依据的可行性与识别率问题进行了论证，证明膝关节角度、踝关节角度或3 个下肢关节角度的组合带有足够的个人信息，是可以用来进行生物识别的。2017 年，丁辉[7]利用Photo Shop CS5软件对采集的人员行走图像进行标记测量，对头部倾斜角、左腿前摆角、左大腿后摆角、左小腿后摆角等9 项指标进行统计，结合9 项指标累计计算出的识别能力可达较高水平。2020 年，桑伟波[8]通过Codamotion 三维动作分析系统对受试者足部特征进行研究，分析个人左右足特征的稳定性和不同人特征的差异性，再采用基于曲线相似度的评价方法进行个人识别。

本文采用英国Codamotion 三维动作分析系统对人体膝、踝关节角度数据完成采集，对采集后的数据引入均值、预估标准差的方法进行初步处理，在此基础上提出了基于最长公共子序列（LCSS）算法对膝关节角度与踝关节角度角度变化曲线相似度进行评估。

1 仪器设备与算法分析

1.1 Codamotion三维动作分析系统工作原理

Codamotion 三维动作分析系统由英国Charnwood Dynamics公司研发生产，是当前世界上最先进的三维动作捕捉系统之一。该系统采用捕捉红外点的方式对粘贴到人身的标识点（maker）进行空间位置检索[9]。Maker 点体积小，可实现无线链接，对人体正常行动不会产生影响并且Codamotion 系统可以实现多个maker 点同时检测的功能，因此可以一次性完成步态数据的采集。Codamotion 系统软件可获得包括位置、加速度、速度、动作时间、身体旋转角度变化等诸多参数，同时可以保证超过5 m内的精度可达0.05 mm，并可自动生成报告和分析。

1.2 LCSS算法曲线相似度测量

在曲线相似度测量领域中相关算法很多，如基于点匹配的方法包括时间翘曲函数（DTW）[10]、编辑距离（EDR）[11]、最长公共子序列（LCSS）[12]等。

其中DTW 算法常用于语音识别中，该算法适用数据曲线形状相似，但是这些形状在x轴上不能对齐的数据相似度测量，由于不同人之间关节角度运动曲线归一化后的数据在形状上均表现出较高相似，因此使用DTW 算法会存在不同人之间的相似度值计算过高的情况。而EDR 算法是对某一序列进行删除、添加、替换的操作实现与其他序列达到相同时，通过对操作次数的统计完成相似性评估，该算法从差异性角度实现两序列的相似性评估，因此在对噪点较为敏感，会直接影响算法运算结果。LCSS 算法通过求两数据之间公共的子数据，子数据并不要求在原数据上连续，通过统计子数据的长度实现两原始数据的相似性评估，该算法从同一性的角度完成相似性评估。

人体关节角度数据的特点在于同一人数据表现出整体趋势重合度高，存在非本质差异。而不同人数据之间表现出整体趋势的类似，但存在本质的差异。在对人体步态数据进行相似性评估时，需要充分考虑数据之间相同点与差异点的关系。因此本文将采用LCSS 算法对Codamotion 系统所提取的下肢步态数据进行计算分析，从而对同一人步态稳定性和不同人步态差异性进行评估。

LCSS算法中，假设现在有两个长度分别为n和m的两条序列点集合为A={a1，a2，…，an}和B={b1，b2，…，bm}，那么最长公共子序列的长度为：

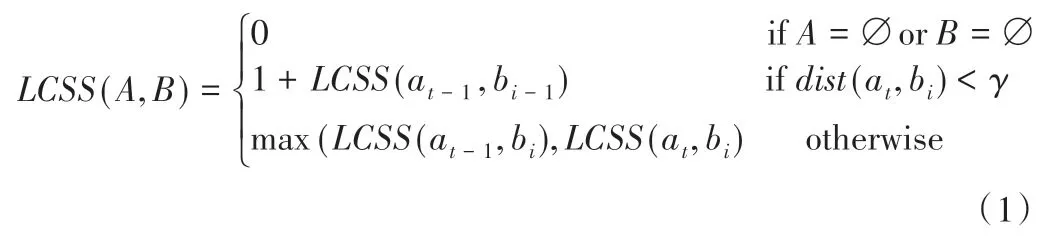
其中t=1，2，3，…，n；i=1，2，3，…，m；γ为设置的距离阈值；LCSS（at，b）i为序列A在轨迹点ak和序列B在轨迹点bi前的最大公共子序列长度；dist（at，b）i为A轨迹中的第at个点与B序列中第bi个点间的距离。可以看出，该方法获取的是符合点间距离阈值的轨迹点数，用来衡量曲线的相似。两条序列点集合A、B的匹配率为ρ的计算方法为：

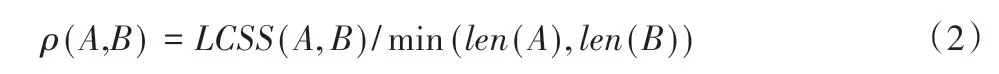
其中ρ（A，B）∈[0，1]；且ρ（A，B）的值越大则表示A序列与B序列越相似。

2 膝、踝关节运动曲线的提取与处理

2.1 实验数据的提取

使用Codamotion系统共采取47人（男生23人，身高172～185 cm。女生24 人，身高160～170 cm）的自然行走膝、踝关节角度数据。对实验人员数据采集完成后通过Codamotion 系统的“Caculatian”中的“Vector Angles”数据计算功能在人体前进方向和竖直方向即x-z坐标上的投影进行矢量角计算。进行矢量角度定义时，膝关节的角度由向量ab与cd的夹角构成；踝关节的角度由cd与ef的夹角构成。如图1所示。

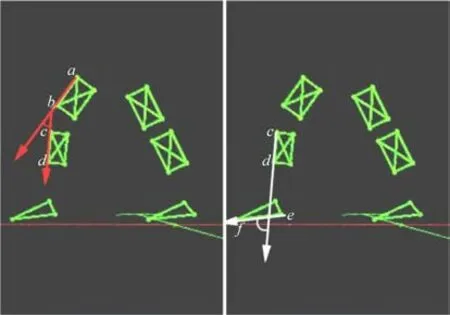
图1 Codamotion测量膝、踝关节角度示意图

2.2 实验数据的预处理

采集过程中由于衣物、行走震动等多种因素会对实验数据造成不可避免的影响，因此需要对实验数据进行筛选。选取记录完整，反映真实的曲线。在对关节角度数据提取完成后可视化发现，Codamotion 系统提取出的数据为最原始的maker 点在空间中的坐标信息，因此需要对数据进行归一化操作。图2 所示为通过多次自然行走所采集到的同一人膝关节数据。由图中可以看出，同一个人相同关节的角度变化曲线并不是一成不变的，而是具有一定的差异性。造成这种情况的原因有很多，比如人员本身行走时的不稳定因素；在行走过程中maker 点可能会因为行走时产生的震动而发生位移；在操作员标记固定好maker 点后实验人员误触或者衣物的遮挡；Codamotion 系统本身采集maker点存在细微误差等。

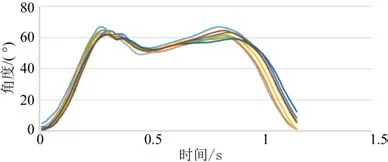
图2 同一个人膝关节角度曲线

考虑到LCSS 算法的计算特点同时为提高准确度需要对算法阈值（γ）进行判断，为此提出以下方法对原始步态数据进行处理分析。以膝关节角度为例，具体步骤如下。

第一步：提取A 同学膝关节角度变化原始数据Ai（i＞1）组，其中A1=（x1，x2，x3，…，xn），A2=（y1，y2，y3，…，yn）；A3=（z1，z2，z3，…，zn），…，Ai=（t1，t2，t3，…，tn）。对这i组数据的对应项元素求平均得新的元素为Wf，其中f=1，2，3，…，n，由Wf（f=1，2，3，…，n）可以组成一组新的关于A同学的膝关节角度数据，记作A新。得到数据A新后，将A新作为A同学膝关节角度变化的标准数据。

第二步：将A新的数据与归一化处理后的数据进行预估标准差计算，再求平均得出同一人膝关节角度变化曲线的合理误差范围γ。计算公式为：

通过式（3）可以得出γ的具体值，而该具体值仅是基于A同学的i组数据计算出的膝关节合理误差范围，因此仅对A 同学的膝关节角度变化具有一定的适用性。如果需要对多数人的合理误差范围进行计算则需要采集足够数据依据该方法计算得出。合理误差范围γ的作用，在对同一人的数据进行分析时，可以将在合理误差范围内的两个不同数据值视为相同数据值进而降低采集过程中多种因素造成的数据误差；通过进一步数据处理之后直接使用LCSS 算法进行相似度分析可以提高判别的准确度。

3 膝关节、踝关节运动曲线相似度分析

在研究人体正常行走时关节角度运动曲线的相似度，主要采用同一人各自比较的方法与不同人交叉比较的方法。分析出同一人相似度的指标数据与不同人之间相似度的指标数据。

在对同一人运动曲线相似度进行分析时分为3 步。第一步，将多组归一化的数据采用求平均的思想计算出“标准数据（A新）”；第二步，计算多组归一化数据的合理误差范围（γ）值作为LCSS 算法的判断阈值；第三步，利用多组归一化的数据依次与“标准数据（A新）”采用LCSS 曲线相似度算法进行相似度评估得出对应每组的相似度值。

在对不同人运动曲线相似度进行分析时。第一步，基于归一化的曲线数据计算的“标准数据（A新）”作为不同人之间交叉比较的数据；第二步，对多人的数据各自分析后计算出各自的合理误差范围（γ）；第三步，对多个人的合理误差范围（γ）求平均得到不同人的合理误差范围（E）值作为LCSS算法的判断阈值；第四步，对“标准数据（A新）”使用判断阈值（E）进行交叉比较分析。

3.1 同一人膝关节、踝关节曲线相似度分析

对47 人（男生23 人，身高172～185 cm。女生24 人，身高160～170 cm）实验人员数据使用Excel数据分析软件进行数据可视化处理之后对膝关节、踝关节角度数据进行分析，每个人的各自相似度分析都由各自的8 组归一化数据与标准数据A新进行相似度量计算，相应每名实验人员则存在8 个相似度值，47 人膝关节、踝关节分别376 个相似度值，依次求出相应的膝关节角度相似度值如图3 所示，踝关节角度相似度值如图4 所示。

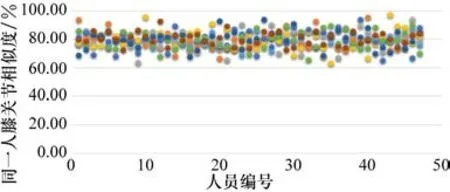
图3 同一人膝关节相似度散点图

图4 同一人踝关节相似度散点图

通过大量同一人膝关节运动角度数据分析使用LCSS 算法进行相似度衡量，对数据进行可视化同一人膝关节运动角度相似度均在60%～100%之间，而踝关节运动角度相似度则在60%～95%之间。通过对每名实验人员的数据各自求平均，其膝关节运动角度总体平均相似度值为79.47%。踝关节运动角度总体平均相似度值为75.34%。

在对平均相似度进行统计分析时，发现同一人膝关节、踝关节相似度分布呈高斯正态分布，同一人膝关节在70%～90%之间的占到膝关节数据量的91.55%，如图5所示。同一人相似度在65%～85%之间的占到踝关节数据量的92.10%如图6 所示。结合总体平均相似度值膝关节79.47%、踝关节75.34%，引入统计学概念3Sigma 准则，求得Sigma 值分别为膝关节6.01%、踝关节6.57%。因此可以推断出若存在两组未知膝关节数据相似度（79.47%+18.03%）即为高度符合，而踝关节相似度（75.34%+19.71%）即为高度符合。

图5 同一人膝关节相似度数据分布直方图

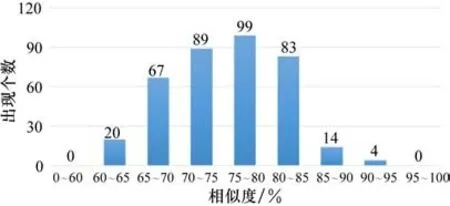
图6 同一人踝关节相似度数据分布直方图

3.2 不同人膝关节、踝关节运动曲线对比相似度分析

以47 名实验人员的数据为基础（男生23 人，身高172～185 cm。女生24 人，身高160～170 cm），通过计算得出每名实验人员的标准数据A新，同时求出γ值为2.0513。由于男女之间身高体态差异较大，此次则以男生23 人、女生24 人分别进行关节运动曲线对比相似度分析。男生两两对比可以得出253个相似度值，女生24人两两对比可以得出276个相似度值，因此膝关节、踝关节分别529个相似度值。

图7 不同人膝关节数据对比相似度散点图

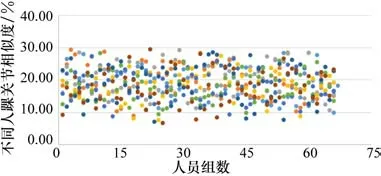
图8 不同人踝关节数据对比相似度散点图

对不同人膝关节使用LCSS 算法进行相似度评估之后，采用最近邻平均相似度进行分析，即考虑每名实验人员与之对应相似度最高的值进行求平均、方差计算。通过数据筛选出实验人员对应最高相似度膝关节、踝关节分别47个值，如图9、图10所示。

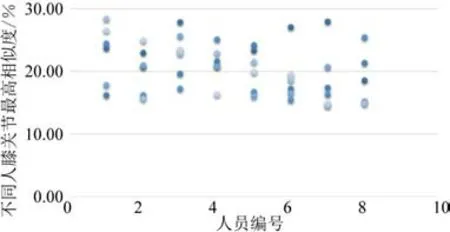
图9 不同人膝关节最高相似度值散点图

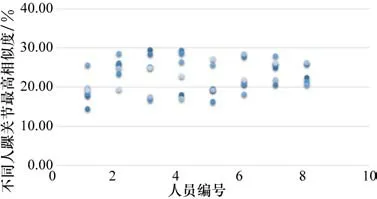
图10 不同人踝关节最高相似度值散点图

根据最高相似度值的出不同人之间膝关节平均最高相似度值为20.52%，标准差为4.06%。不同人之间踝关节平均最高相似度为22.85%，标准差为4.10%。

因此可以推断若两组未知膝关节数据相似度小于20.52%即存在较大差异，而两组未知踝关节数据相似度小于22.5%即存在较大差异。

4 结束语

人体步态特征属于动态特征，相较于指纹、DNA 等实物证据存在一定程度的变化性，但在短期内人的行走动态特征呈稳定的周期性变化，并且不同人之间的行走特征也存在巨大差异。因此，当前人体步态特征作为法庭证据仍需要进一步深入研究，但在侦查领域却能为侦查人员提供有效线索。

本文应用LCSS 算法并根据具体实验数据计算相应阈值大小实现对同一个人膝、踝关节角度曲线数据相似度评估，对不同人的膝关节、踝关节角度曲线数据进行交叉比较分析。实验表明，若存在两组未知膝关节数据相似度（79.47%+18.03%）即为高度符合，而踝关节相似度（75.34%+19.71%）即为高度符合。对不同实验人员数据交叉比较时，若存在两组未知膝关节数据相似度小于20.52%即存在较大差异，而两组未知踝关节数据相似度小于22.5%即存在较大差异。

目前该算法在实际操作中鲁棒性较低，在实际操作中单从膝关节或踝关节数据实现人身识别，具有一定的风险性。因此考虑到如何能将膝关节数据、踝关节数据特征等其他关节特征数据进行结合分析判断，这样便可以在理论上大大提高识别的准确率，进一步强化该算法的实际可操作性。