由概率统计谈数据分析能力的培养

广东省中山市第一中学(528400)刘忠华

数据分析是基于一定目的进行数据收集、整理、加工,并从中提炼出有价值信息的过程.数据分析既可以是现状分析、原因分析,也可以是预测分析.一个或多个科学、准确的数据结果,无论是对现状的识别、未来可期的收益或是优化重要决策都十分有意义.因此,数据分析能力是人生中的一项重要能力,中学生正处于可塑可造的关键阶段,抓住这个阶段利用概率统计内容的特点,进行数据分析能力的培养是一项有意义的教学举措.

1 重视思想方法,培养随机性数学思维意识

概率统计思想由概率思想和统计思想两部分组成.概率思想是通过观察和研究随机现象,发现随机现象背后的统计规律, 理解随机现象.统计思维是指利用所获得的数据, 根据问题得出统计结论.近年来,高考试题的运算要求有所弱化, 加强了对概率统计的考查.因此, 我们应重视培养学生的随机性数学思维,即通过对数据的收集、整理和分析,充分认识随机数学的本质及其与形式的关系.曾经的广东高考题:“某数学老师身高176cm,他爷爷、父亲和儿子的身高分别是173cm、170cm、和182cm.因儿子的身高与父亲的身高有关, 该老师用线性回归分析的方法预测他孙子的身高为____cm.”借助这么几个数据对孙子的身高进行预测,为了随机性与盲目性,题目明确要求用线性回归的方法进行分析.

统计中也存在着很大的不确定性, 当分析一组数据时,可以用平均数、中位数、众数、方差(或标准差),还可以用极差.所使用的方法与问题的实际情况有关,甚至与数据的分散程度或重点有关.如: 省乒乓球队决定在小张与小王中选拔一人进行省队,他俩近期对阵时的成绩如下:

?

你是教练,你如何选?

一看输赢: 都赢五场,也都输五场;胜负平均,无高低之分.

二看平均得分: 小张的平均得分12.2;小王的平均得分12.2,不是冤家不对头,又是一样.

三看得分的中位数: 小张的中位数是11;小王的中位数也是11;又是相同.

四看得分的众数: 由排列结果,可以看出众数又都是11;

……

怎么办?

最后, 小张的标准差s小张≈ 4.24, 小王的标准差s小王≈4.38, 由于小张的标准差小于小王的标准差, 说明小张的发挥更稳定,因此,选小张.

又如在一份成绩单中,有的强调平均分,有的强调及格率或优秀率, 有的侧重于方差看班级成绩分布的离散程度.通过培养学生的随机思维,使学生认识到现实生活中不仅有数学的不确定性,而且有数学的随机性.在不确定性思维过程中要培养良好的数学随机思维,提高对各种问题的认识.

在教学中,学生不仅要用随机数学思维来描述随机现象,还要体会回归思想、独立性检验思想、抽样思想在数学中的应用实验.概率统计问题不仅是一种教学问题,而且是指导学生思维方式和学习方式的问题,使学生更好地理解和掌握知识.

2 注重数据分析方法的指导,帮助学生提高数据分析能力

学生掌握的数据分析方法也有很大差异,加强对学生学习数据分析方法的指导有两种方法.一是注重统计模型的构建过程,二是注重处理方法在教学中的渗透.

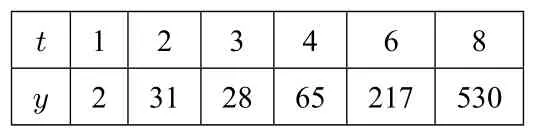
如: 在研究某细菌繁殖速度时,得到时间t 与细菌个数y之间的数据如下:

?

根据上表数据,当时间为10 时,细菌个数的个数.

甲同学: 建立在散点图的基础上,很容易发现y 与t 具有线性相关关系,于是,计算相关系数得r = 0.9267,可见借助散点观察的结果没有问题.于是,得t,y 之间的线性回归方程为=72.29t-146.1,令t=10,得=577;

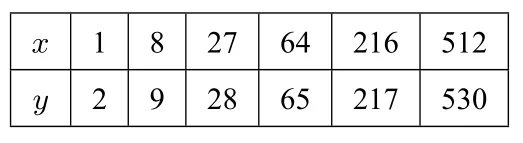
乙同学: 根据数据特点看出y 与t3具有线性相关关系,于是,令x=t3,将所给数据转化为下列数表:

?

再计算相关系数r′= 0.9999, 可见乙同学的判断准确.立得时间t 与细菌个数y 之间的回归方程=1.032t3-0.586,再令t=10,得=1031.

这两个数据的的差别太大了,谁正确? 两个的计算都没错.结论的可信度应该是乙的高一点,因为从相关系数也可以看出这一点;但乙的做法又并不可取,因为,只有当两个变量不具有线性相关关系时,才能将数据进行转化.本题中的两组数据具有线性相关关系,因此,我们没有必要再去对它进行变换.

构建模型是分析数据的前提.分析数据要求学生能够选择合理的统计模型,得出结论,即对数据的理解和处理,为以后的数据解释做准备.因此,学生能否熟练地运用概率统计模型,在实际问题的过程中选择或建立合理的模型进行数据分析和处理,直接决定结论得出的合理性,并能成功地解决这一问题.数据分析的过程也是建立推理模型的过程,这是学生易犯错误的一部分.因此,在教学中,教师可以创设各种各样的问题,如实际情境、数学情境、科学情境等.根据不同情境下解决实际问题的需要,指导学生如何比较选择统计模型的优缺点,从而合理选择或构建解决实际问题的模型.例如,根据收集到的数据绘制了“环境温度与昆虫产卵数”这两个随机变量形成的散点图,线性回归模型或非线性回归模型能更好地拟合回归方程吗? 通过实际计算、比较和分析,学生可以比较两种模型的估计值和实际值之间的差异,评价和比较未来数据中可能出现的变化,从而找出最接近实际的模型.因此,合理选择统计模型具有重要意义.通过对统计模型“好”与“坏”的分析,将随机试验的思想应用到统计中,建立合理的实验模型,以提高数据分析能力,不断调整通过最小二乘法和极大似然估计,将该模型应用于实际.

3 培养数学阅读能力,加强数学思维

提起数学阅读能力,大家首先想到的应该是数学材料分析、数学语言理解,而在概率统计高考试题中还包括对应用问题材料的解读,理解生活与数学的联系,从中抽象出数学关系,能将实际问题数学化,以此找到解题方法.读懂、理清、弄通、会做是高考对数学阅读能力的要求.对于高考试题题目,既要保持数学的严谨性,又要保持信息的全面性.一般情况这类题目都比较长,所以对数学阅读能力的培养有一定的现实意义.

我们看一个问题: 某地2020年第二季度应聘和招聘人数排行榜前5 个行业的情况列表如下:

?

?

若用同一行业中应聘人数与招聘人数比值的大小来衡量该行业的就业情况,则根据表格中数据,就业形势一定是( )

A.计算机行业好于化工行业

B.建筑行业好于无聊行业

C.机械行业最紧张

D.营销行业比贸易行业紧张

阅读是一方面, 理解更重要, 本题计算机、营销、机械这3 个行业的应聘人数与招聘人数比值分别为: 1.732、1.502、1.945,又化工的比值小于1,故A 错.建筑的比值小于≈0.853,物流的比值大于≈1.061,故B 对,因贸易的比值不定,可以很大,故C、D 都错,所以选(B).

本题给出很多数据,阅读这些数据如何快速的找到重点是求解的关键.

身处“大数据时代”的我们,既要接受这种快餐文化,也要适应数字阅读方式,而作为数学学科的分支,教师既要把握学生的阅读能力水平,又要传播时代热点.数学阅读并非简单的文字浏览,相反地是许多学生没有真正的掌握数学阅读技巧,换句话来说,就是要通过数学思考,把属性相同的知识进行抽象概括.

例如在学习必修三第二章“随机抽样”时,教师就可以引导学生进行联想,与初中所学过的统计知识类比,学生必定会产生一些疑问,此时教师要及时鼓励学生说出自己的疑问,要有敢于提问、敢于质疑的能力;如果学生没有及时发现问题,这就说明学生还未掌握数学阅读技巧,让学生自己标注难点问题,教师在课堂中将以前的知识联系起来,帮助学生理解,针对性解决问题,让学生更好地理解.在实际课堂中,教师不仅要注重学生的能力,同时也要尽可能多地发觉自己手中教材的价值,将数学教材作为提高学生阅读能力和解题能力的重要工具.教师应及时关注数学教材所扮演的角色,解析教材编写的规律与意义,以此作为提升学生阅读能力的资料.教师需要在课堂上有意识地为学生设置让学生交流和表达的机会,让学生自由的表达,然后再规范其数学用语,改变传统教学中单一的由教师用数学语言描述数学知识,多给与学生语言表达和数学阅读的机会,通过不断地练习,提高自身能力,教师仍然要以数学教材为基础,不可脱离教材,也不可脱离实际生活,切不可让学生盲目阅读.

4 积极开展统计调查活动,创设数据分析素养培育的环境

目前的概率与统计教学大多以课本为中心,教师选用现实问题作为情境,设计问题进行统计教学的机会较少,指导学生参与统计调查实践活动的机会更少,久而久之学生对其统计意义的理解就过于片面.学生很少完整地参与数据分析的全过程,即收集数据、整理数据、分析数据、解释数据.似乎平时的练习题和考试题更多地是对已经收集整理好的理想数据(计算量小、数据涵盖信息少)进行粗加工的机会较多,因此碰到具体问题时感觉到无从下手.事实上,学生在参与统计调查实践活动的过程中,自然会经历数据分析的全过程.这样的活动也为教师选择学生熟悉的真实案例融入教学提供了素材.在活动过程中,学生进一步体会了数据分析的方法在解决现实问题中的应用.

开展统计调查实践活动为学生经历数据分析的全过程提供了机会,其中的每个环节都会用到具体的分析数据的方法.例如收集数据就要用到随机抽样,整理数据就要用到统计图表对数据进行可视化描述,分析数据就要用到多种模型,解释数据就要用到相关性强弱等等.解决实际问题时,选择的每一种分析数据的方法是否合理,是要放在整个数据分析的过程中去理解的,看这种方法是否达到了最终的统计目的,对总体的估计效果如何.因此,要理解选择某种分析数据的方法的合理性,应该放在数据分析的全过程中进行教学.

5 总结

综上所述,在学习高中数学统计部分时,应注重对学生数据意识的培养,注重完善学生对统计知识的掌握,加强对学生学习数据分析方法的指导.与此同时,教师也要不断加强自身的专业学习,切实提升自身的数据分析素养,充分发挥信息技术的优势,努力实现技术与教学的深度融合.