数学化生活问题,提升数学建模能力*——篮球定点投篮的数学建模问题研究

广东省惠州市第八中学(516000)袁东升

数学建模是数学学科六大核心素养之一.《普通高中数学课程标准(2017年版)》指出,数学建模是运用数学的知识与方法,通过建立数学模型去解决现实问题,培养学生应用意识与实践能力[1].面对纷繁芜杂的现实生活,我们要引导学生学会从中提炼问题,建立相应的数学模型,分析求解出结果,并指导生活实践,有利于进一步提高学生学习数学的兴趣,发展学生的创新精神.

我们将对篮球定点投篮过程中的数学建模问题进行研究与分析.

1 问题提出

篮球是一项常见的体育运动,尤其是体育明星投篮或扣篮时那种勇猛而又优雅的动作,更是让人羡慕与钦佩.众所周知,篮球比赛的方式是将球投入对方篮筐,根据得分的多少来确定胜负.因而投篮的命中率就成了取胜对方的关键[2].

为简化问题的研究,我们只讨论篮球定点投篮时的情况.不妨从数学的视角作如下讨论: 为保证篮球能顺利投入篮筐,

1)最小投射角应该有多大?

2)篮球出手时的初速度与投射角度之间有什么关系?

3)篮球投射角度与入射角度之间有什么关系?

4)在篮球运动中,运动员越高大,在比赛中是否越有优势?

2 模型假设与模型建立

篮球从出手到入篮筐的过程可分为两个部分: 一是篮球从出手到即将入筐的过程,无需考虑篮球的形状与旋转的情况,可将其抽象为一个质点,此时篮球的运动过程可看作是一个斜抛运动[3].二是篮球从即将入筐到命中的过程,此时要考虑篮球的实际形状及篮筐大小的限制.当篮球球心刚好经过篮筐中心时,篮球将不擦碰篮筐边缘顺利入筐,即空心入筐.

根据物理学知识,若不计空气阻力的影响,只考虑重力的情况,假设投篮时篮球出手后无横向偏角,则篮球将只在运动员出手点、篮球球心、篮筐中心所确定的平面内作斜抛运动,而且所经过的轨迹应该是一条抛物线.

假设运动员在距离篮筐下L 米处投篮,球出手时离地面高度为h 米,篮筐距地面高度为H 米,一般情况下h ＜H.篮球出手时的初速度为v0,以投射角α(0°＜α ＜90°)作斜上抛运动,入筐时的入射角为β(0°＜β ＜90°).

不妨以运动员所在地面上的点O 作为坐标原点, 建立平面直角坐标系(如图1 所示), 则篮球出手时的位置点A(0,h), 篮筐中心点B(L,H).

图1

3 模型求解

3.1 投射角

由前面的假设分析可知,篮球的运动轨迹可看作一条抛物线,不妨设为f(x)=ax2+bx+c(a0)则，有

所以篮球的运动轨迹对应的函数为

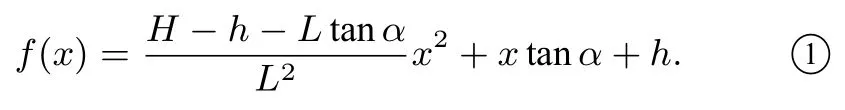
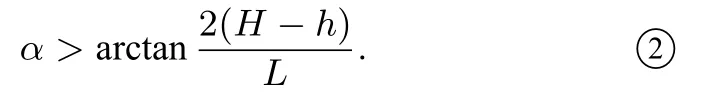
显然,当运动员离篮筐的距离L 保持不变的情况下,投篮时篮球出手高度h 越大,篮球投入篮筐所需的投射角度α就越小.

3.2 出手初速度与投射角的关系

假设篮球出手时的初速度为v0,重力加速度为g,篮球从出手到进入篮筐经过的时间为t,则要使篮球顺利投入篮筐必须满足如下条件:消去时间t,可得

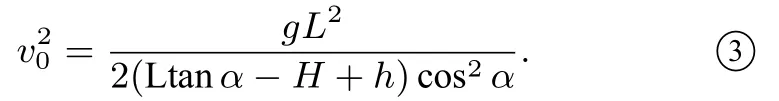
将上述方程转化为关于tan α 的一元二次方程

根据国际篮联的规定, 篮筐高度的统一标准是H = 3.05m, 三分线距离篮筐中心的水平距离L =6.75m, 重力加速度g = 9.8m/s2.用Geogebra 模拟篮球出手时的最小初速度v0_min与出手高度h 之间的关系(如图2所示).由图像可知,篮球出手时的最小初速度v0_min是出手高度h 的减函数,也就是说篮球出手高度越大,球出手时所需的最小初速度就越小.

图2

由以上结论可知,当投篮距离L 及出手高度h 保持不变的情况下,运动员越高大,起跳后越容易达到所要求的出手高度h,在篮球比赛中自然是越有优势.这就是在现实比赛中,篮球队的运动员普遍都比较高大的原因.

3.3 投射角与入射角的关系

由于在篮球即将入筐时,篮球已不能看成质点.在篮球入筐的瞬间,其运动轨迹可近似看成是匀速直线运动进入篮筐.对于斜飞过来的篮球,其入射截面应该是篮筐在垂直于篮球入射速度方向上的投影,为一个椭圆形[3].如图3 所示,当篮筐的半径为R,篮球的半径为r 时,该椭圆的长半轴为a=R,短半轴为b=R sin β.

图3

为使篮球球心经过篮筐中心,必须满足入射截面的短轴2b 不小于篮球的直径2r.即2b ≥2r,整理可得

按国际篮联的规定, 篮筐内缘直径为2R = 45cm,标准男子比赛用篮球直径为2r = 24.6cm.故篮球入射角β ≥33.14°.根据导数的几何意义, 由函数①可得+tan α = -tan β 解得篮球顺利入筐时,投射角α 与入射角β 之间的关系为

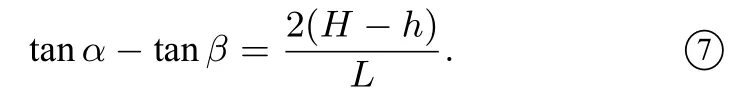
4 模型检验

在方程④中,解得

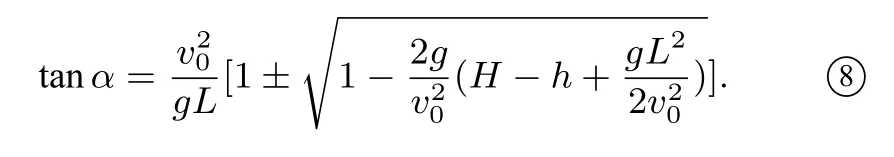
当一位身高1.8m 的运动员,在距离篮筐下L=4m 处定点投篮,测得球出手高度为h = 2.25m,初速度为v0= 8m/s,由式⑧可得篮球投射角度α ≈69.81°或α ≈32.49°,两者均满足式②(α ＞arctan= arctan 0.4 ≈21.80°).这也就意味着这个运动员有两个出手投射角度,究竟应该选哪一个呢?

不妨用Geogebra 模拟篮球的运动轨迹(如图4 所示).线段CD 表示篮筐在篮球运动轨迹平面中的投影区域,实心圆F,B 分别表示篮球运动到点F,B 时的位置.显然当投射角为69.81°)时,篮球可顺利入筐;当投射角为32.49°)时,篮球在点F 处碰到篮筐边缘C 而被反弹回去,不能顺利入筐.也就是说只有当投射角为69.81°),篮球才能顺利入筐.

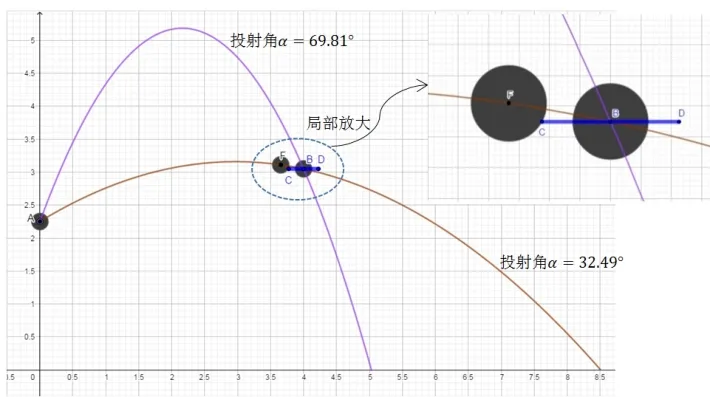
图4

为什么会出现这种现象呢?

这是因为在前面假设分析时, 将篮球抽象成一个质点.而在篮球入筐时,篮球的尺寸相对于篮筐,已不能看成一个质点,必须考虑篮球实际大小的影响.

当篮筐的半径为R,篮球的半径为r 时,要使篮球顺利入筐,必须满足

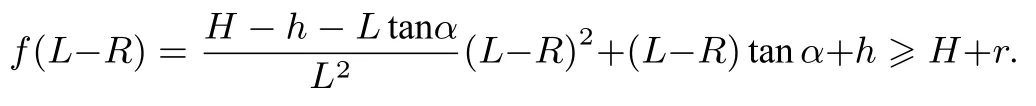
解得

令L = 4,H = 3.05,h = 2.25,R = 0.225,r = 0.123,可得α ≥ 44.74°.所以在题设条件下, 只有当投射角α ≥44.74°时, 篮球才能顺利入筐, 否则篮球将会被篮筐边缘弹射回去.

5 小结

综合前面的分析求解,我们得到了篮球定点投篮空心入筐的理论条件,确定了篮球投射角、出手初速度、入射角之间的相互关系式.

具体结论如下: 要使篮球顺利投入篮筐,

2)篮球出手时的最小初速度为 v0-min=对应的投射角为α =arctan

4)投射角α 与入射角β 之间必须满足关系式tan α-tan β =

上述篮球定点投篮运动的数学建模分析求解过程,有利于引导学生学会将生活问题数学化,进一步提升数学建模能力.同时也为篮球运动员训练及实战比赛提供了一定的参考价值,有利于他们提高篮球命中率,轻松赢得比赛.