基于改进聚类算法的人工神经网络短期负荷预测研究

甘景福， 晏 坤， 马明晗， 贺鹏康， 田新成

(1.国网冀北电力有限公司唐山供电公司， 河北 唐山 063000； 2.华北电力大学电力工程系， 河北 保定 071000)

1 引言

变压器负荷预测是绕组热点温度预测和日方式制定的关键环节，传统负荷预测一般基于相似日或简化的负荷模型，但区域负荷和当地经济、气候、产业构成以及用电习惯有很大关系，不同地区的用电规律不同，不存在普遍适用的负荷预测模型，传统方法针对性和预测精度均不足[1-3]。随着计算机科学技术的迅猛发展，通过机器学习算法对历史负荷、气象等数据进行学习和建模，针对性地建立输入、输出量之间的非线性映射关系，极大提高了各种场合下的负荷预测精度，许多专家学者在该领域进行大量相关研究[4]。

文献[5]提出一种基于遗传算法的灰色神经网络短期负荷预测方法，利用灰色模型弱化数据的随机性，并采用遗传算法对神经网络进行优化，提高了预测的精度，但该方法并未研究历史数据的优化问题。文献[6]研究了一种基于前馈人工神经网络(Back Propagation Artificial Neural Networks, BP-ANN)与多层聚类历史数据处理的短期负荷预测方法，相比传统方法在预测精度上有一定的提升，但数据处理仅采用聚类算法筛除了异常负荷样本，没有对样本进行分类选择，也未考虑负荷本身存在的冲击及噪声数据。文献[7]采用小波分析对历史数据进行平滑处理并基于BP-ANN进行负荷预测，但小波去噪只能去掉历史数据中的冲击及噪声干扰，对于检修、停电等异常数据无法甄别并剔除。

训练样本对神经网络的影响作用甚至超过神经网络自身结构，因此提供准确的样本对提高预测精度十分重要。对于大量原始样本，若全部选用，会导致神经网络训练速度过慢；若随机抽取，数量较少但有用的样本可能会遗漏，导致得到预测模型稳定性差。且由于原始样本中负荷冲击、噪声和异常数据的影响，不进行有效处理会导致训练得到的网络预测误差偏大[8]。为了解决上述问题，本文提出了一种采用小波分析结合改进聚类算法对样本进行优化选择的神经网络预测方法，并通过仿真与原方法进行了比较。

2 负荷样本的优化处理

2.1 负荷曲线平滑处理

工业负荷较多的地区，负荷曲线往往含有较多的瞬时冲击数据，可采用小波阈值去噪进行平滑处理。原理是基于某一小波基对负荷曲线进行多尺度分解，并对不同尺度下分解得到的小波系数设定阈值，当小波系数大于阈值时，作为信号的有用分量得以保留，当小波系数小于阈值时则认为主要由噪声组成而被滤除[9,10]。与傅里叶频域滤波去噪相比，小波阈值去噪能在滤除噪声的前提下尽可能多地保留波形的形态和局部细节，减少数据的失真，并且其运算速度更快。

各层阈值λN可依据公式设定：

(1)

式中，M为首层小波分解系数绝对值的中位数；KG为高斯噪声标准方差的调整系数；N为信号尺度。

对于连续的Doppler信号，sym8小波去噪效果更好，小波分解尺度的选取对于去噪性能有较大影响，分解尺度较小时，重构后的信号不易失真但仍保留较多噪声，分解尺度较大时，去噪效果更明显，但可能会滤除较多的有用细节导致处理后的数据失真[10-12]。基于sym8小波在5尺度下对负荷曲线滤波如图1所示，由图1可知经小波阈值去噪处理后，原始负荷曲线中的尖峰被滤除，波形更加平滑，但形态并未发生变化。

图1 负荷曲线小波去噪平滑处理Fig.1 Smoothing of load curves by wavelet denoising

2.2 样本的筛选分类

当无停电、检修及临时方式调整等偶然因素作用时，负荷变化具有较强的规律性，因此可利用聚类分析进行筛选分类，依据类别选取样本用于神经网络训练。相比随机选取，聚类分析优势是防止样本数较少的类别被遗漏或选取的数量过少，从而提升训练样本特征的完整性，同时减少训练样本的数量，降低异常样本干扰，在提升训练速度的同时提高了预测精度。

负荷曲线的k-means聚类原理是通过比较各样本与聚类中心欧式距离，将样本归类到距离最小的聚类中心，并更新聚类中心，不断重复迭代直到所有聚类中心都收敛为止。将类内距离和类间距离指数度量方法与k-means聚类相结合，称为基于有效指数的k-means聚类算法[13]。该方法可动态调整参数k并计算有效指数，使各分类在类内有较高的聚集性，而类间则有较高的分散性，使聚类结果达到最优，当聚类数为k时有效指数Kc(k)可表示为：

(2)

式中，Sj、Cj分别为第j个分类的曲线和对应的聚类中心；Ck1、Ck2为当分类数为k个时的两个不同聚类中心；Ns为数据集中数据的个数。

曲线的聚类是一种基于形态差异的分类方法，基于这一特性可对具有非典型形态的曲线进行识别。传统有效指数k-means聚类方法未考虑异常曲线对分类数的占用问题，导致有用数据未被准确分类。基于有效指数聚类的特点，本文在已有算法的基础上引入对异常曲线的识别和过滤流程，将样本数量过少的分类过滤并重新聚类，确保聚类结果可靠，其流程图如图2所示。

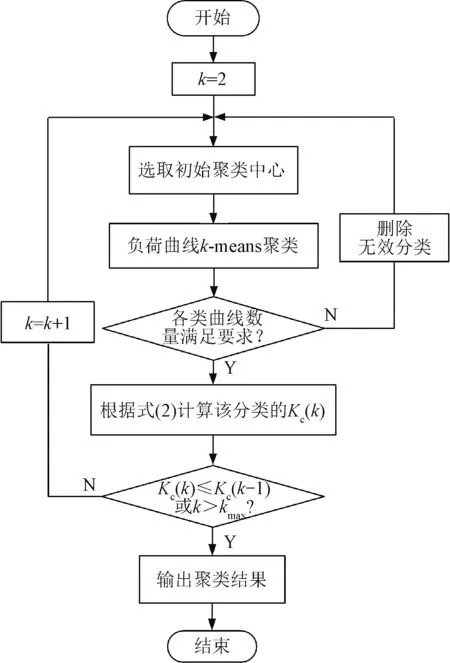
图2 改进的k-means聚类算法流程Fig.2 Process of improved k-means clustering algorithm

3 人工神经网络负荷预测

3.1 负荷预测模型

BP神经网络是众多机器学习算法中比较基础的一种，由于良好的非线性拟合能力，成为负荷预测常用的手段之一。其原理是将预测误差反向传递，通过求误差对各层权值或阈值的导数，沿导数的负梯度方向不断对权值或阈值进行调整，直到预测误差在允许范围内[14]。BP神经网络通常由输入层、隐含层以及输出层三层网络构成，其隐含层可以有多层，但一般系统采用一层隐含层即可，隐含层节点数m可依据经验公式确定：

(3)

式中，n为输入节点数；l为输出节点数；α为1～10之间的整数。

根据负荷变化规律可知，预测日温度和天气对负荷影响较大，节假日、双休日负荷曲线与工作日亦有明显差异，且预测日负荷是在前一日负荷基础上随着预测日的天气、气温以及日类型而相应变化，因此神经网络输入设置为28×1维向量，包括预测日前日整点24×1维负荷值，另4个输入分别为预测日最高、最低温度、预测当日天气及类型，输出为预测日整点24×1维负荷值。实际预测时，模型的输入通过在线进行实时更新，预测模型如图3所示，该模型可根据前24 h负荷和预测时段的天气、气温预报对未来24 h的整点负荷进行在线预测。

图3 神经网络短期负荷预测模型Fig.3 Neural network short term load forecasting model

预测日类型和预测日天气为非数值量，作为输入需要分别进行量化处理。预测日类型主要包含法定节假日、双休日和工作日三类，可分别量化为0、0.5、1；预测日天气量化方法见表1。

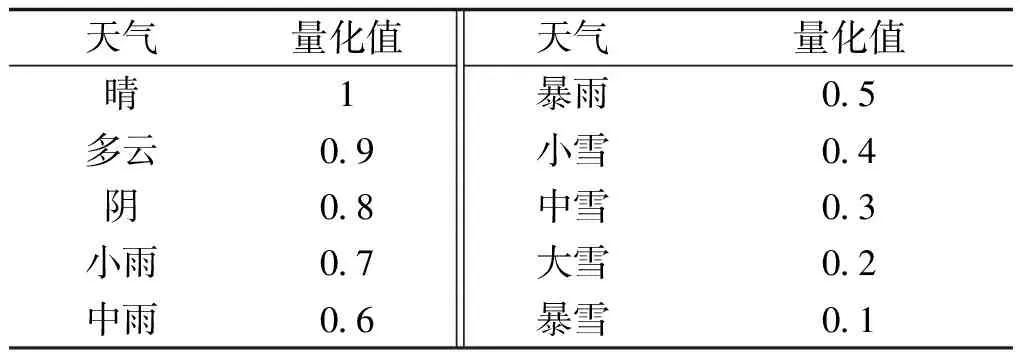
表1 天气情况量化表Tab.1 Weather quantification table

神经网络输入层权值wia和输出层权值vab的更新公式为：

(4)

式中，xi为神经网络输入层第i个输入；ha为隐含层第a个节点的输出；yb和yd_b分别为输出层第b个节点的输出和期望输出；f′为隐含层激励函数对隐含层输入量的导数；F′为输出层激励函数对输出层输入量的导数；η为学习率，η∈(0,1)。

不同类数据的量纲和数据尺度不同，为避免影响权重的差异，需对数据进行归一化处理，使所有数据范围压缩到[0,1]之间，min-max归一化公式为：

(5)

式中，xmin和xmax分别为输入样本的最小值及最大值。

隐含层激励函数采用sigmoid函数：

(6)

输出层激励函数为：

F(x)=x

(7)

3.2 模型评价指标

第s个预测值yp(s)与对应的真实值yr(s)的绝对误差为：

Ep=yp(s)-yr(s)

(8)

多个预测值的平均误差为：

(9)

式中，Nc为误差值的数量。

平均相对误差反映多个预测值的整体误差：

(10)

均方根误差PRMSE反映多个预测值偏离真实值的程度，其值越小说明预测结果越稳定，均方根误差为：

(11)

引入相关系数R对神经网络多日负荷整体预测性能进行评价，R越趋近于1则代表模型的性能越好。

(12)

4 短期负荷预测算例

以某地区一台容量为50 MW的变压器2020年365条日负荷曲线为原始样本，进行小波阈值去噪处理得到的平滑曲线如图4所示。

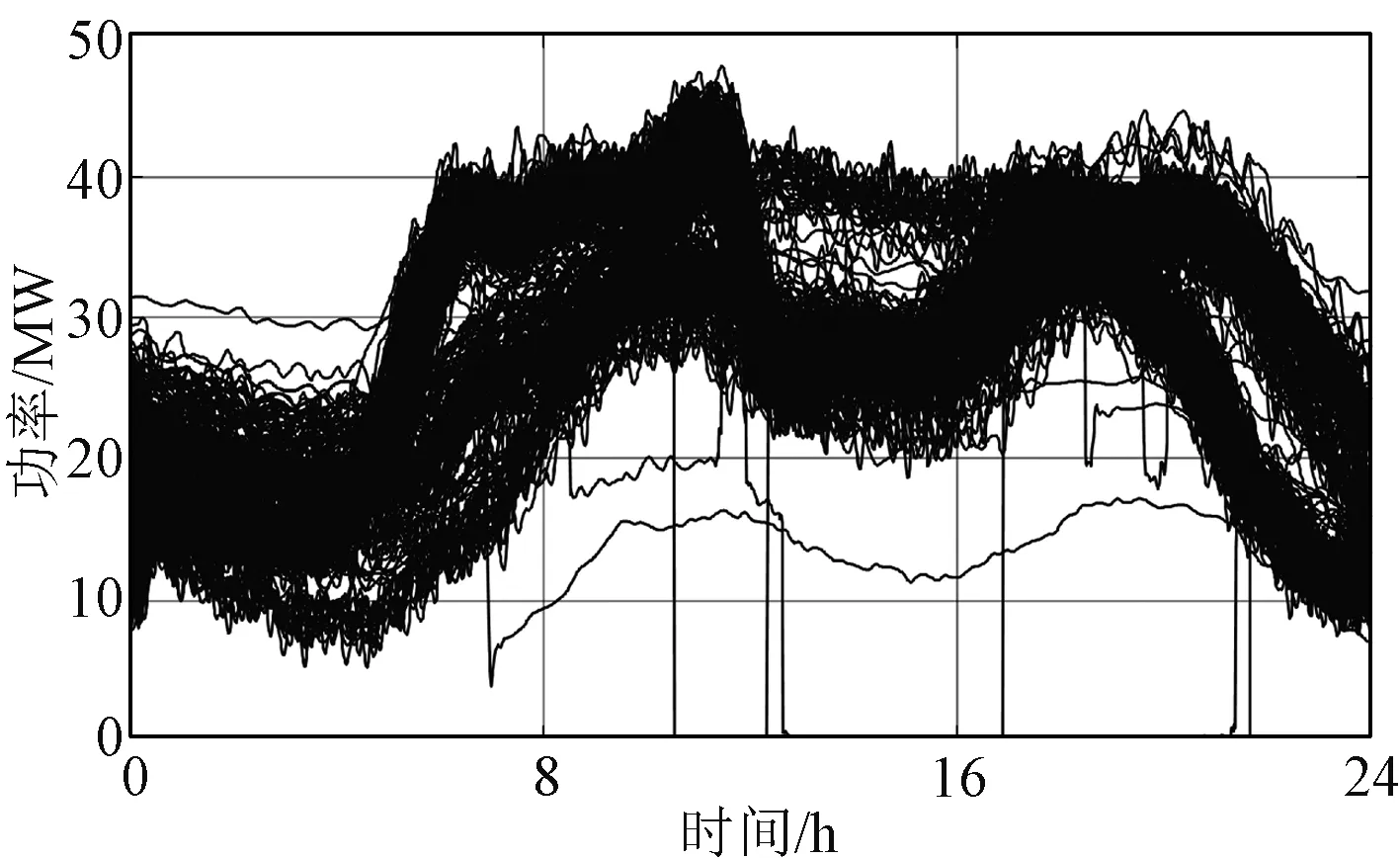
图4 去噪平滑后的负荷曲线Fig.4 Load curves after denoising and smoothing

对上述负荷样本进行归一化和聚类，当聚类上限kmax设置过小时，不同形态的曲线可能被归为同一类，过大时又会导致聚类速度太慢。为得到准确的类别并提高聚类速度，可根据去噪后的曲线簇形态估计一个大概的分类上限值，根据图4估计kmax=6。聚类结果见表2和图5，经改进k-means聚类后样本被划分为4类。图5(a)～图5(c)分别为三类负荷曲线，其中粗线为该分类的聚类中心，图5(d)为筛除的异常曲线。由聚类结果可见，该主变的日负荷曲线有三类典型形态，其中第一类样本数量较少，第二类、第三类数量较多，且有11个异常样本被筛除。训练所用样本仅从聚类得到的典型样本中选取，除负荷数据外还包括对应的日类型和天气、气温等其他输入参数。训练样本选取的原则是当各类样本数量都足够多时，每类取相同数量，若某类数量过少则可全部选用。

表2 负荷样本聚类结果Tab.2 Clustering results of load samples

图5 改进的k-means负荷聚类结果Fig.5 Load clustering by improved k-means algorithm

为进行对比分析，用三种不同方法得到的样本训练神经网络，并采用相同的样本测试其预测性能。测试集样本分别从聚类后的三类负荷样本中各选取10个组成。训练集样本选取方法为：

方法1：除测试集样本外，余下的335个样本均纳入训练集；方法2：除测试集样本外，从余下的335个样本中随机抽取60个纳入训练集；方法3：除测试集样本外，从本文所提方法获得的三类样本中各随机抽取20个纳入训练集。

将全部负荷曲线进行降维处理，变换为整点负荷曲线，利用Matlab建立图3所示结构的网络，其隐含层神经元在8～17个之间，经试验对比确定最佳隐含层神经元个数[15]，学习率为0.01，分别采用上述三种方法得到的样本对神经网络进行训练。以测试集三类样本的负荷预测结果为例，图6(a)～图6(c)为其中三天的负荷预测结果，预测误差统计见表3。

图6 预测值与实际值对比Fig.6 Comparison between prediction value and real value

表3 不同样本选取方法预测误差对比Tab.3 Prediction error comparison of different samples selection methods

对比可以看出，方法1中三类负荷预测精度均不高，但彼此间差距较小；方法2中预测精度较低，尤其是占比少的类别预测误差很大，原因是样本个数少的分类在训练样本中占比较低，训练不充分；方法3的平均误差和均方根误差较前两种更小，且各类预测误差比较接近，说明采用本文所提样本优化方法后，各点负荷预测精度和稳定性均得以提高。

为了进一步对比分析模型的整体预测性能，以天为单位，统计平均误差、平均相对误差、均方根误差以及相关系数，对测试集中30个预测日负荷进行预测，三种方法所建模型各项性能指标对比见表4，可见方法3的平均误差EM、平均相对误差PM、均方根误差PRMSE以及相关系数R均明显更小，模型训练时间Ttrain更短，因此综合分析上述算例结果可知，训练样本经小波阈值去噪平滑和改进的k-means聚类筛选处理后，不同情况下的负荷预测精度、稳定性以及速度改善均较为明显，整体预测性能有了较大提升。

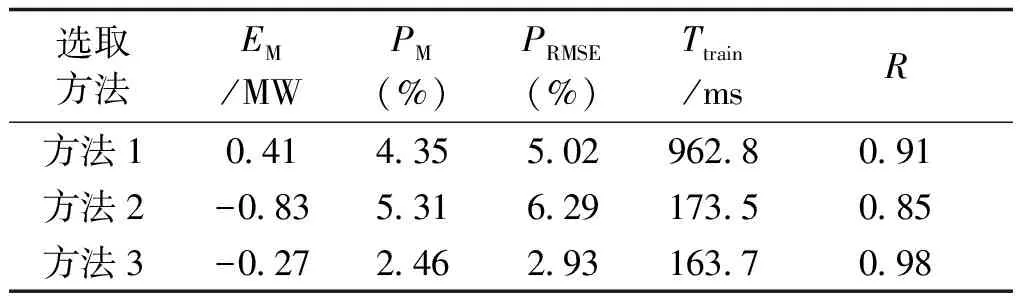
表4 不同样本选取方法整体预测性能对比Tab.4 Comparison of overall prediction performance of different samples selection methods

5 结论

BP神经网络常用于电网短期负荷预测，其预测精度与所选用的训练样本有直接关系。由于电网的停电、检修、方式调整以及冲击负荷的存在使得负荷样本中常包含尖峰、噪声及异常数据，导致无法建立准确的神经网络模型。同时，训练样本随机选取容易遗漏数量较少的类别，影响神经网络模型的泛化性能，致使无法对不同情况下的负荷均作出准确预测。通过采用小波阈值去噪以及聚类分析对样本进行处理，滤除尖峰和噪声数据并筛选出各类典型曲线，通过按类别选取训练样本，可实现对训练样本的优化处理，据此建立的神经网络负荷预测模型相比全部选用或随机选取训练样本，其训练速度、预测精度和稳定性得以明显提升。