基于混合遗传算法的高速公路桥梁风屏障参数优化
罗颖,廖楚峰,韩艳†,蔡春声,2,何旭辉,李凯
(1.长沙理工大学土木工程学院,湖南长沙 410114;2.路易斯安那州立大学土木与环境工程系,路易斯安那州巴吞鲁日70803;3.中南大学土木工程学院,湖南长沙 410075)
近些年来,由强风作用所导致的高速公路交通安全事故频发,不仅危及人身安全,也给经济财产造成了巨大损失.为提高车辆在强风作用下的行驶安全性,目前最常用的措施是在桥梁主梁两侧设置风屏障,以改善车辆行驶风环境,减小风荷载对车辆的影响[1].
目前国内外已有多位学者通过风洞试验、数值模拟与现场实测等研究方法,结合空气动力学,从车辆的流场分布、气动力系数及动力响应等方面对风屏障的防风效果开展了研究分析.葛盛昌等[2]在强风地区铁路干线两侧设置挡风墙,通过现场实测发现设置挡风墙能大大降低其内侧的风速.Coleman等[3]通过风洞试验测试了有无风屏障情况下的车辆气动特性,结果表明风屏障能有效减小车辆气动力系数.Chen等[4]基于风洞试验和CFD数值模拟,分别得到桥梁及车辆的气动力系数,计算并对比了有无风屏障时桥梁及车辆的动力响应,分析了风屏障对行车安全性的影响.结合风洞试验和数值模拟,何玮等[5-6]探讨了风屏障参数对车桥系统的影响,发现风屏障参数的变化对列车阻力系数的影响较为明显,且列车位于迎风侧时其气动特性对风屏障参数的变化更为敏感.
以上研究仅限于风屏障参数对车桥系统气动性能的影响,缺乏对风屏障参数优化的研究.针对该问题,向活跃等[7]通过风洞试验测试不同高度风屏障下车辆的气动力系数,以车辆的风荷载突变量作为评价指标,基于数据包络法(DEA)评估了风屏障的防风效果,但只能在已有的方案中进行选择,容易陷入局部最优,且只是基于对列车影响的风屏障高度优化.为了开展对车桥系统影响的风屏障参数优化,苏洋等[8]通过风洞试验与数值模拟计算了不同高度风屏障下车辆及桥梁的气动力系数,以车辆倾覆力矩与桥梁阻力系数作为优化目标,为了避免DEA 方法易陷入局部最优及多目标优化不能直接判断个体优劣的缺点,引入NSGA-II&DEA 混合算法探讨了风屏障高度的优化,但只是风屏障的单一参数优化.向活跃等[9]基于改进的网格搜索法,以车辆气动特性为目标函数,建立了风屏障防风效果的优化模型,对风屏障的高度和透风率进行优化.然而,上述研究只将桥梁与车辆的气动力系数作为研究目标,没有直接反映风屏障参数对车桥系统响应的影响,且主要针对铁路桥梁,较少涉及到公路桥梁.
基于某三塔双索面叠合梁斜拉桥,本文通过风洞试验分别测量桥梁和车辆在不同高度和透风率风屏障下的气动力系数,进而分析得到主梁跨中在静风稳定检验风速下的侧向位移和车辆在设计车速下的失稳临界风速;然后利用多目标遗传算法——NSGA-II,对风屏障参数进行优化,计算得到在不同高度及透风率下的Pareto 解集;最后,根据数据包络法(DEA),计算每个解集中个体的相对效率值,确定风屏障的最优参数.
1 风洞试验
1.1 工程背景
本文基于某三塔双索面叠合梁斜拉桥开展研究,该桥的桥跨布置为(249.5+550+550+249.5)m,具体如图1 所示.主梁采用钢混叠合梁,宽度为30.2 m,边主梁高2.92 m,主梁截面如图2 所示.大桥跨越宽达1 600 m、深约300 m的峡谷,桥面处高300 m,风速较大,需要在两侧设置风屏障以保障车辆的行驶安全性.

图1 桥跨布置图(单位:m)Fig.1 Layout of bridge spans(unit:m)
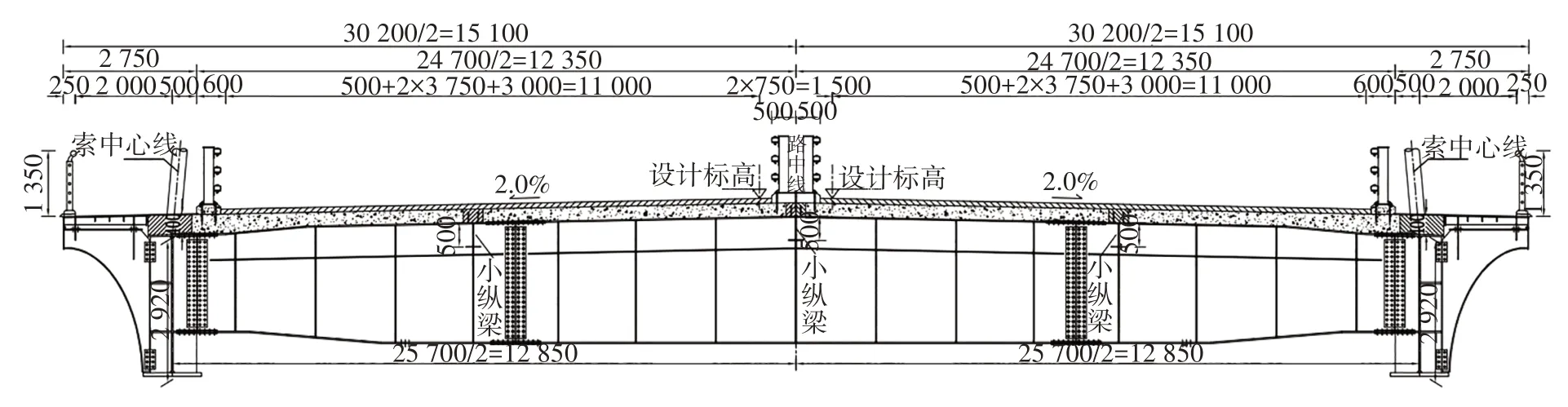
图2 主梁标准横断面图(单位:mm)Fig.2 Standard cross section of main girder(unit:mm)
1.2 试验概况
为了研究风屏障参数对车辆及桥梁气动力的影响,分别开展了主梁测力试验与车辆测压试验.主梁节段模型测力试验在长沙理工大学风洞实验室高速段进行,其尺寸为21 m×4 m×3 m(长×宽×高).主梁节段模型缩尺比取1∶40,如图3(a)所示.车辆测压试验是在中南大学高速铁路建造技术国家工程实验室的高速铁路风洞试验系统进行,其尺寸为15 m×3 m×3 m(长×宽×高).文献[10]表明,相比小轿车,厢式货车更容易发生失稳,因此车辆测压试验中以厢式货车为研究对象,具体尺寸见表1.主梁和车辆模型缩尺比取1∶32,如图3(b)(c)所示.基于以往研究[5-6]考虑最不利情况,仅测量车辆位于迎风侧且垂直于来流时的气动力系数.风屏障透风率依照等效透风率原则分别取10%、20%和30%,见图3(d),高度分别取1.2 m、2.0 m、3.0 m 及4.0 m.试验模型具体如图3所示.
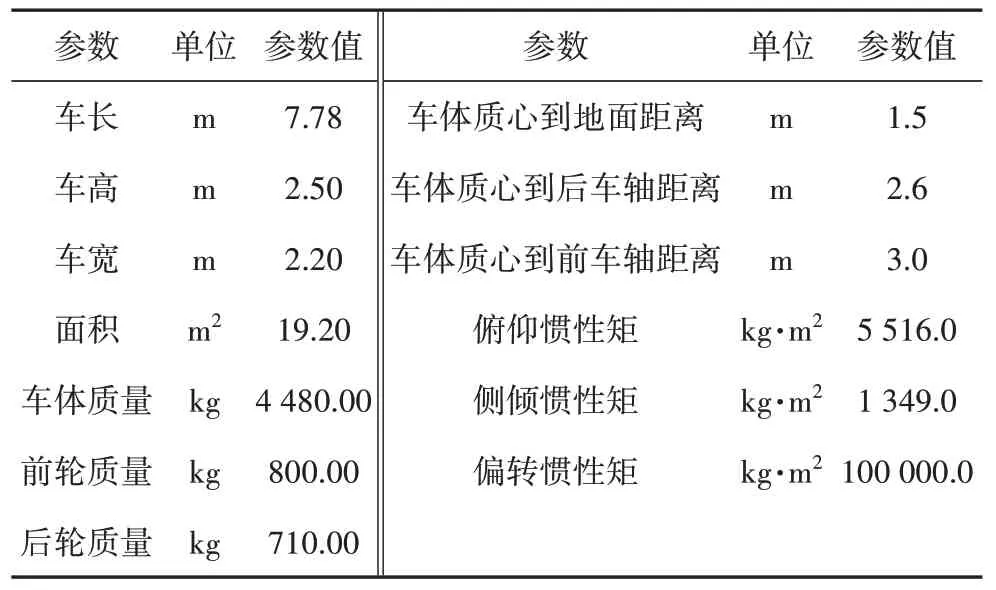
表1 厢式货车车辆参数Tab.1 Vehicle parameters

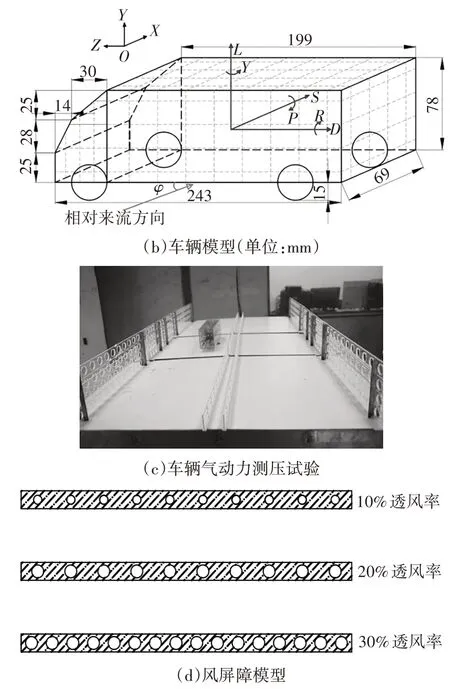
图3 试验模型Fig.3 Test model
1.3 试验结果分析
主梁的三分力系数定义参考文献[11],为简便起见,仅计算风轴坐标系下的主梁气动力系数,公式如下:
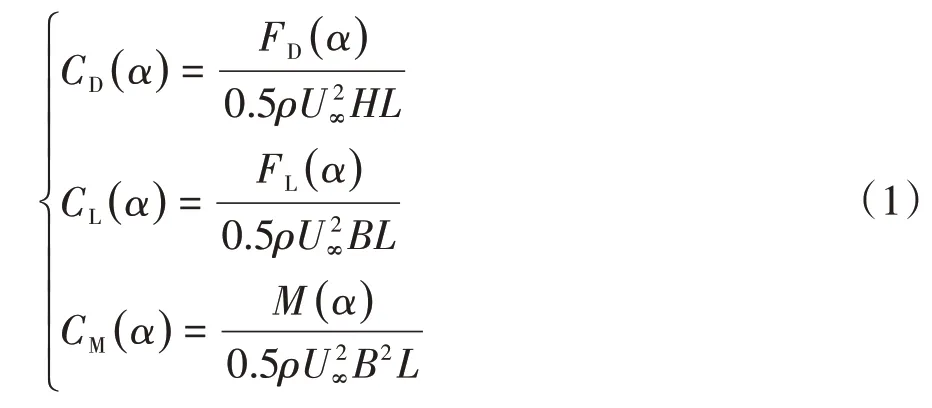
式中:α为风攻角;CD(α)、CL(α)与CM(α)分别为风轴坐标系下不同风攻角对应的主梁阻力系数、升力系数与扭矩系数;FD(α)、FL(α)与M(α)分别为不同风攻角下主梁的阻力、升力与扭矩;U∞为试验来流平均风速,取10 m/s;ρ为空气质量密度,取1.225 kg/m3;H、L、B分别为节段模型高度、长度和宽度.
参考相关文献[5-6],主梁阻力系数CD对于风屏障的参数变化较为敏感.由于篇幅所限,以下仅给出阻力系数CD在不同风屏障参数下随风攻角的变化情况,具体见图4.
从图4 可以看出,在不同风屏障参数下,主梁阻力系数CD随风攻角的变化趋势大体一致,均在0°风攻角附近达到最小值,并随着风攻角绝对值的增大而增加.这是由于0°风攻角下的主梁断面整体阻风面积最小,随着风攻角的变化,主梁阻风面积逐渐变大.当风屏障高度较小时,CD对风屏障透风率的变化较为敏感,但达到一定高度后透风率的影响作用减小,且均在0°风攻角附近透风率的影响较大.这是因为0°风攻角附近风屏障透风率的变化对主梁整体阻风面积的影响较大,而在大攻角下风屏障透风率的变化引起阻风面积的变化相对主梁自身阻风面积已经较小.

图4 主梁阻力系数变化图Fig.4 Variation diagram of the drag coefficient for the girder
针对这类大跨度斜拉桥,参考文献[12]对此桥进行了三维非线性静风响应分析,得到桥梁的静风响应.通过对比-5°~5°风攻角下的跨中侧向位移,-5°风攻角下的侧向位移最大,因此后续选取该风攻角下的情况予以分析.-5°风攻角下主梁跨中侧向位移随风屏障高度及透风率变化趋势如图5所示.

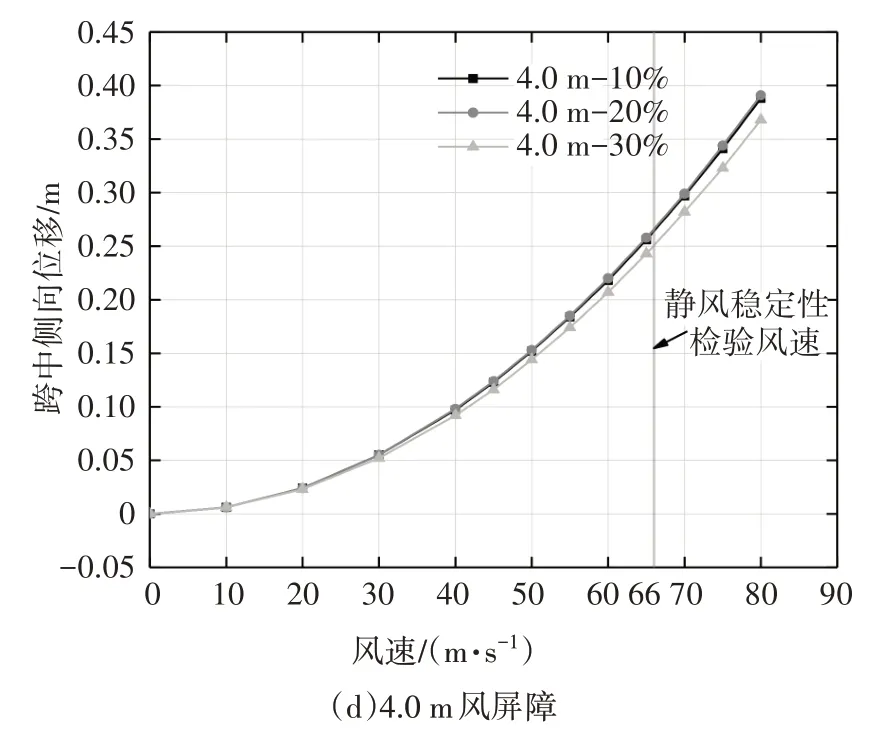
图5 主梁侧向位移变化图Fig.5 Variation diagram of the lateral displacement for the girder
由图5 看出,主梁的侧向位移随着风屏障透风率的减少而增加;但随着风屏障高度的增加,透风率的影响逐渐减弱,这主要是由于风屏障高度达到一定值后,风屏障透风率的变化对于桥梁气动力的影响减小,这与主梁三分力系数的变化大体一致.根据参考文献[11]计算得到此桥的静风稳定检验风速为66 m/s,将该风速下的主梁侧向位移作为反映风屏障参数对于桥梁影响的指标,位移越小则桥梁越稳定,结果见表2.

表2 风速66 m/s下的主梁跨中侧向位移Tab.2 Lateral displacement of the midspan for the girder under the wind speed of 66 m/s m
从表2 可看出,主梁跨中侧向位移的变化趋势与主梁阻力系数CD的变化趋势是一致的,随着风屏障高度的增加、透风率的减少,侧向位移增大.但是4 m 高度下并不完全符合这个趋势,最大值出现在20%透风率的情况,这可能是因为此时主梁的阻力系数相差不大,升力系数和扭矩系数对侧向位移的影响变得突出.
车辆气动力系数的处理参考文献[13],定义如下:
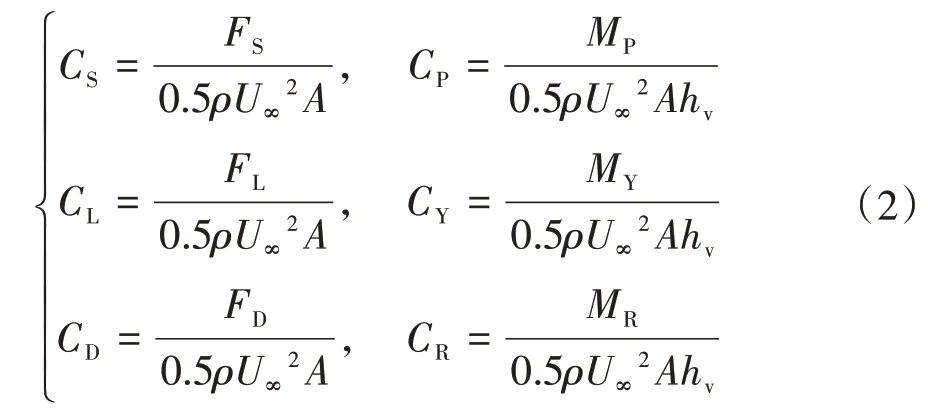
式中:A为车辆迎风侧面积;hv为车辆质心距车辆底面距离;CS、CL、CD、Cp、CY和CR分别为车辆的侧向力系数、升力系数、阻力系数、俯仰力矩系数、偏转力矩系数和侧倾力矩系数;FS、FL、FD、MP、MY和MR分别为作用于车辆质心的侧力、升力、阻力、俯仰力矩、偏转力矩和侧倾力矩.
将车辆气动力进行处理,对风屏障参数变化较敏感的侧向力系数CS的试验结果如图6 所示.可以看到,车辆的侧向力系数CS随着风屏障高度与透风率变化的规律与主梁三分力系数的变化是相反的.

图6 车辆侧力系数随不同风屏障参数的变化图Fig.6 Variation diagram of lateral force coefficient for the vehicle under various parameters of the wind barrier
基于表1 厢式货车参数,编写程序计算车辆静力失稳临界风速,将车辆在设计车速下行驶出现车轮反力为0 时作为临界失稳状态[10],结果如表3 所示.由表3 可以看出,车辆临界风速变化规律与车辆气动力系数变化规律大体上是一致的.但是在30%透风率下,4.0 m风屏障下的车辆临界风速小于3.0 m风屏障下的,这是因为在3.0 m 和4.0 m 的高度下,侧力系数相差较小,由侧力系数差异产生的影响不明显,临界风速由其他5个气动力系数所控制.

表3 车辆临界风速Tab.3 Critical wind speed of the vehicle
2 NSGA-II&DEA 多目标优化模型
2.1 多目标优化模型及结果
以往风屏障参数优化大多是通过调整风屏障高度或透风率以达到车辆安全行驶的目的,属于单目标优化问题(Single-objective Optimization Problem,SOP)[7].然而,随着桥梁跨度增加,风屏障对于桥梁的作用也不容忽视,即需要同时考虑风屏障对车辆和桥梁的影响,此时涉及多目标优化问题(Multiobjective Optimization Problem,MOP).多目标优化问题通常表示为在一组约束条件下使得多个目标函数都趋于最大化或最小化,以最小化优化为例,其具体描述如下:
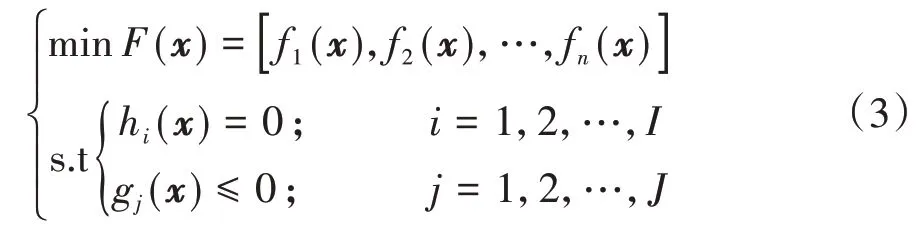
其中:l维向量x={x1,x2,…,xl}为决策变量,包括l个决策变量.式(3)表示了n个优化目标函数的多目标最小化优化问题,l为决策变量个数,I为等式约束的数目,J为不等式约束的数目.
多目标优化算法根据具体算法采用相应的筛选机制对个体进行筛选,最终得到一组无法直接比较优劣的解集,也就是说在该解集中无法做到对一目标函数进行优化的同时而不减弱其它目标函数,一般称该解集为Pareto最优解[8].
本文采用基于Pareto 最优概念的多目标遗传算法——NSGA-II[14-16](Non-Dominated Sorting Genetic Algorithm-II).相比于上一代算法,NSGA-II 能够有效提高对Pareto 解集的计算效率,同时保证种群的多样性和结果的优良性.其具体流程如图7所示.
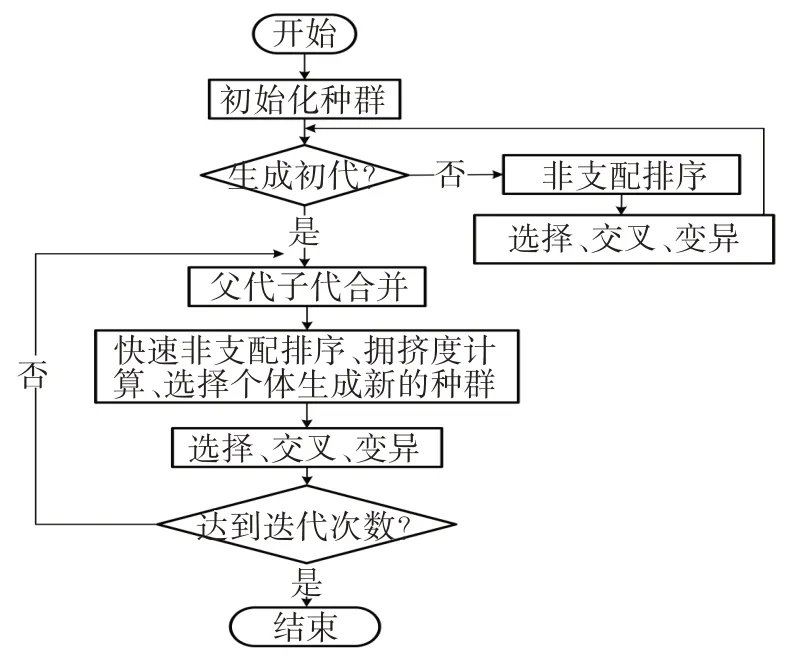
图7 NSGA-II基本流程图Fig.7 Basic flow chart of NSGA-II
以桥梁跨中侧向位移最小与车辆的临界风速最大为优化目标,由于风洞试验成本较高,仅对有限的几个风屏障参数下的车桥气动力系数进行了测试,同时对两个参数进行拟合精度不够,因此分别对风屏障的高度和透风率进行优化.根据表2 中的结果,分别将主梁跨中侧向位移随风屏障高度和透风率变化的曲线采用多项式函数进行拟合[8].同理,基于表3结果,分别将车辆临界风速随风屏障高度和透风率变化的曲线采用多项式函数进行拟合[8].其拟合误差均较小,拟合形式如式(4)(5):
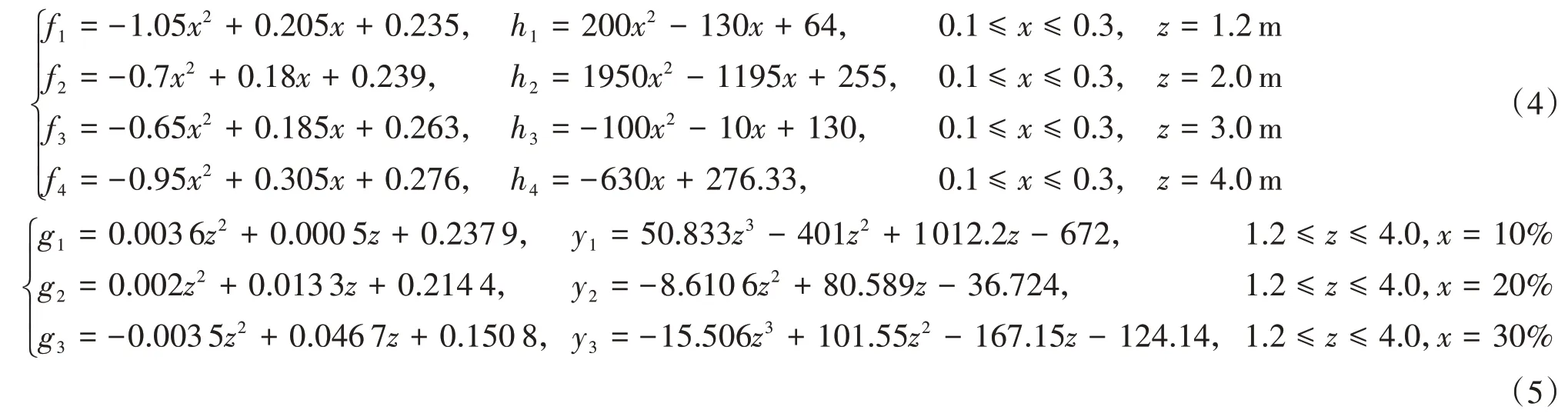
式中:fi和gj为桥梁跨中侧向位移随风屏障参数变化的拟合函数;hi和yj为车辆临界风速随风屏障参数变化的拟合函数;x和z分别表示风屏障透风率和高度;式(4)表示不同风屏障高度下fi和hi分别随风屏障透风率x变化的函数,i∈[1,4];式(5)表示不同风屏障透风率下gj和yj随风屏障高度z的变化函数,j∈[1,3].
参考相关文献[8,14-16]编写NSGA-II 算法,参照文献[8]设置NSGA-II 算法的参数:目标函数个数为2;种群数量N取100;迭代次数取600;编码方式采用实数编码;交叉概率Pc取0.9;变异概率Pm取0.1.遗传算法进行最小值优化,由于优化目标是使桥梁跨中侧向位移函数fi、gj值尽可能小,车辆临界风速hi、yj值尽可能大,因此将hi、yj进行预处理,采用其倒数1/hi、1/yj,多目标优化数学模型见式(6):

基于式(6)所表示的优化模型,对各个参数进行优化计算得到Pareto 解集.由于遗传算法的个体产生具有随机性,使得结果可能会在一定的范围存在误差,因此通过多次重复计算以减小算法自身带来的随机误差.优化结果如图8和图9所示.
图8和图9为NSGA-II程序计算得到的Pareto解集,从图中可以看出Pareto 解集中个体在可行域中分布均匀,且不同高度及透风率下的计算结果趋势基本一致.图9(a)中出现的不连续情况,说明在0.255~0.285 之间的个体相对于其它个体并不占优,所以在迭代过程中被淘汰.但是决策者无法直接判断Pareto 最优解集中个体的优劣,为了弥补遗传算法的这一缺陷,本文引入综合评价方法对Pareto 解集进行相对效率值计算.

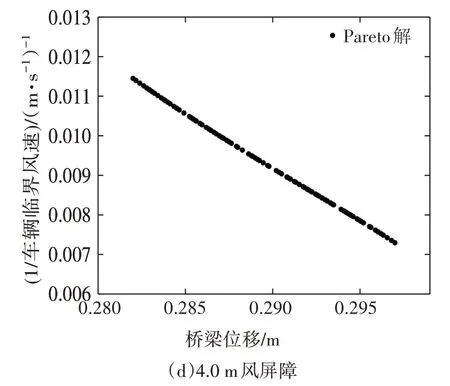
图8 不同风屏障高度下的Pareto解集Fig.8 Pareto solution set considering the wind barriers with different heights
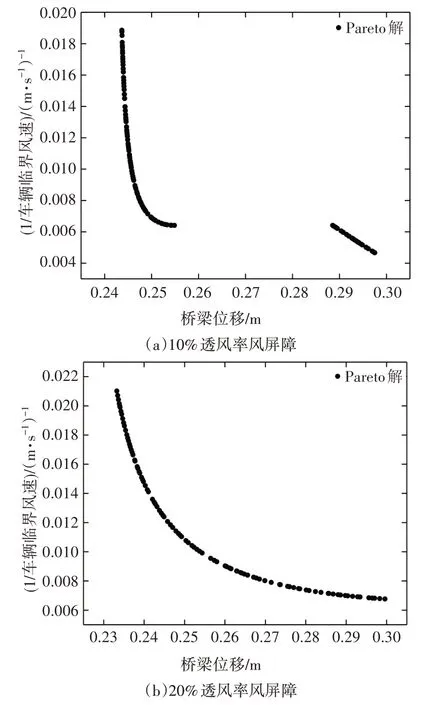
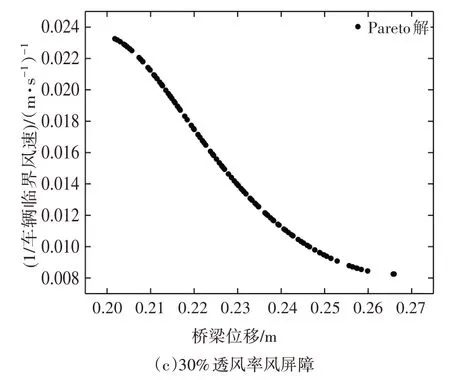
图9 不同风屏障透风率下的Pareto解集Fig.9 Pareto solution set considering the wind barriers with different ventilation rates
2.2 数据包络法原理及结果
综合评价方法中的数据包络法(DEA)[17]相比于其它综合评价方法具有客观性、对输入输出无量纲等优点.该方法包含多种模型,本文采用超效率CCR-DEA(Super-Efficiency-CCR-DEA)模 型[18]对Pareto解集进行相对效率分析.
假设有n个评价对象,记为DMUi(i=1,2,…,n),具有k种输入与m种输出,对i0个决策单元进行评价,则其相对效率评价CCR模型可以构造如下[17]:
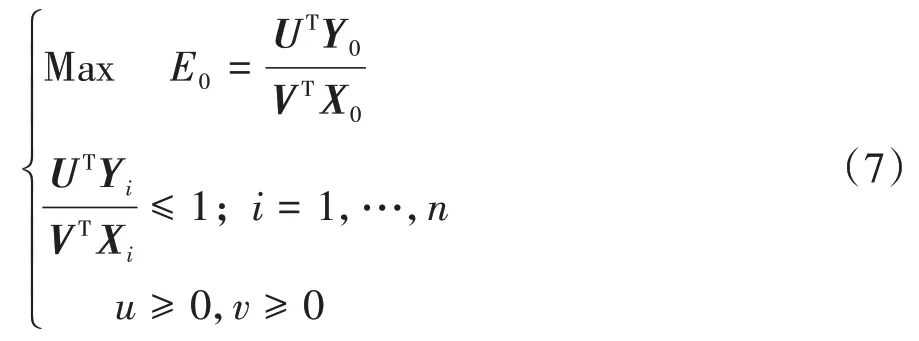
式中:E0为第i0个评价对象的相对效率值;VT=(v1,v2,…,vk)、UT=(u1,u2,…,um)T分别表示输出、输入向量的初始权重值;X0=(x1i,x2i,…,xki)T、Y0=(y1i,y2i,…,ymi)T分别表示输入、输出向量.
然而,CCR-DEA 模型只是区分了效率值的高低,并不能对效率值为1 的个体进行效率排序[18],为此采用超效率CCR-DEA 模型对高效率个体进行排序,模型如下:
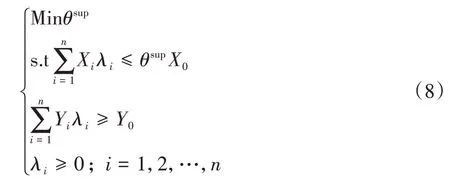
DEA 方法中要求输入最小、输出最大,则相应的评价对象的效率指数越大,对于输入、输出指标要求为非负值且无量纲要求.据此,将主梁跨中侧向位移与车辆临界风速的倒数(即上文计算的Pareto 解集中的个体)作为DEA 的两个输入指标,编写了DEA方法计算程序[7,17-18].对于两个输入指标,其值越小,则主梁跨中侧向位移越小,车辆临界风速越大,对于车桥系统越安全.因此,在程序中对输出指标设置为定值,两个输入指标越小,则相对效率指数E越大,说明风屏障对车桥系统的影响作用越好.对各个工况中DMU 的相对效率值进行计算,结果如图10所示.
由图10 可知:在不同的风屏障高度下,透风率为30%时的相对效率值均为最大,说明透风率为30%的风屏障的防风效果最好.因此,接下来对30%透风率的风屏障在不同高度下的结果进行相对效率值计算,结果见图11.
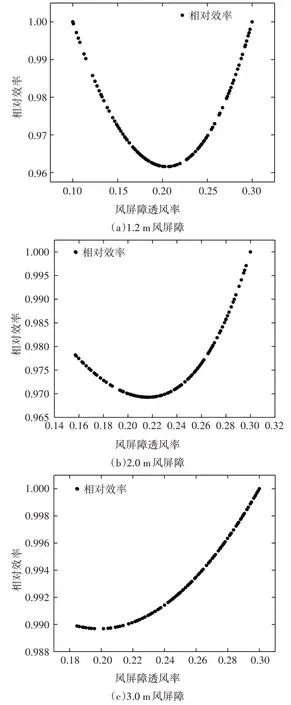
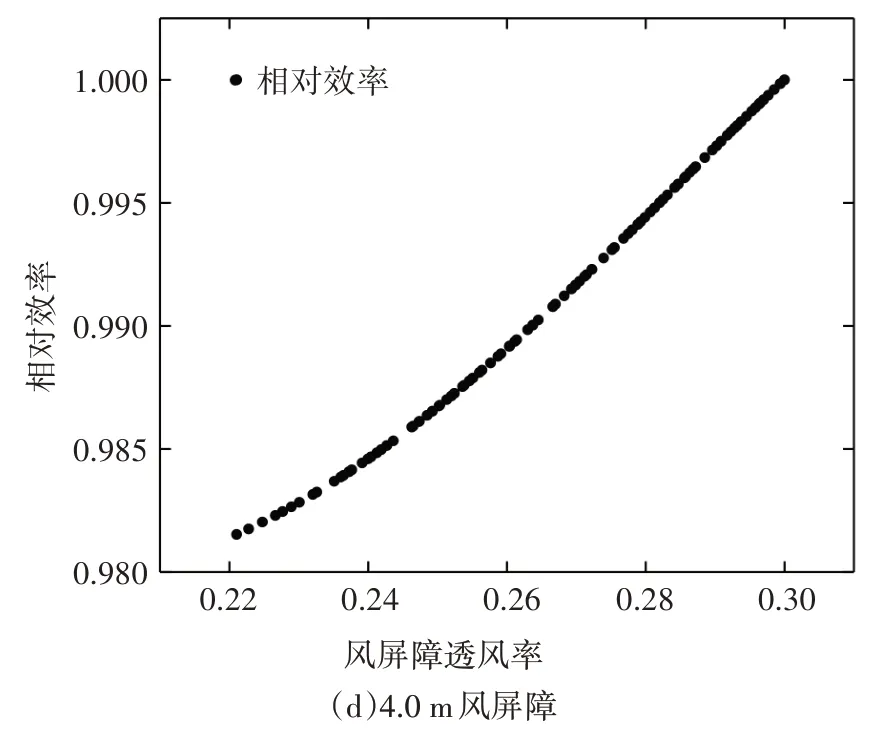
图10 风屏障高度优化结果Fig.10 Optimal results for the wind barriers with different heights
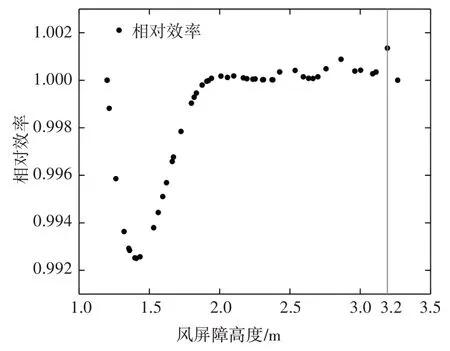
图11 风屏障30%透风率优化结果Fig.11 Optimal result for the wind barrier with the ventilation rate of 30%
从图11 可以看出,有多个个体的相对效率值较为接近,但是并不影响对其进行优劣排序[8,19].通过对比,在高度为3.2 m时,相对效率值达到最大.由此在不考虑经济性的情况下,可以得到高度为3.2 m、透风率为30%的风屏障综合抗风效果最好.
3 结论
本文基于某三塔斜拉桥,考虑了风屏障高度和透风率对桥梁和车辆的影响.以桥梁静风响应与车辆的失稳临界风速为优化目标,将NSGA-II 算法与DEA 方法结合对高速公路桥梁风屏障的高度及透风率参数进行了优化,得到以下结论:
1)主梁及车辆气动力系数随着风屏障的参数变化而变化,呈现一定的规律,随着阻风面积的增大,主梁的阻力系数是增大的,而车辆的侧力系数是减小的.
2)主梁在静风检验风速下的位移、车辆的临界风速分别与其阻力系数和侧力系数的变化趋势基本一致,但随着风屏障高度的增加,趋势发生了改变,这可能是风屏障达到一定高度时,阻力系数与侧力系数随高度变化较小,差异不明显,其它气动力系数的影响起控制作用.
3)将多目标遗传算法NSGA-II 与DEA 方法结合,首先经NSGA-II 算法多次计算得到不同风屏障参数下的Pareto 解集,再利用超效率CCR-DEA 模型对Pareto 解集中的个体进行相对效率计算,得到该桥风屏障在透风率为30%、高度为3.2 m 时对于车桥系统的综合抗风效果最佳.

