一种基于投影几何的空间非合作目标角速度估计方法
董振宇
(沈阳理工大学自动化与电气工程学院,沈阳 110159)
1 引言
近年来,在非合作目标的研究中,由于未知目标的结构等可用信息,估计非合作目标的运动参数一直是一个非常具有挑战性的热点问题,成为了非合作目标抓捕中的关键任务,广泛应用于在轨服务与空间碎片清除。
在轨服务(On-Orbit Servicing,OOS)是在空间通过人、机器人或服务卫星完成延长各种航天器寿命、提升执行任务能力以及维护好空间环境的安全稳定的空间操作。例如,辅助入轨、在轨维修、加注燃料、拖曳离轨。另一方面,近20年来空间碎片已经成为了人类太空活动的重要障碍,空间碎片和航天器碰撞可直接改变航天器的表面性能,造成表面器件损伤,甚至航天器故障。空间碎片还会对轨道资源构成威胁,在同一轨道高度,当空间碎片的密度达到临界密度时,碎片的链式膨胀过程还会造成轨道资源的永久性破坏。
而上述两种应用背景下的捕获阶段中,如图1所示,当系统质心位置发生偏移、惯性参数也会发生改变,可能会引起组合体姿态失稳,需采取协调控制实现捕获后组合体的稳定,否则会使得系统失控从而导致整个抓捕任务失败。所以在抓捕前获取目标的运动参数,以判断能否抓捕目标与制定合适的抓捕方案就尤为重要。
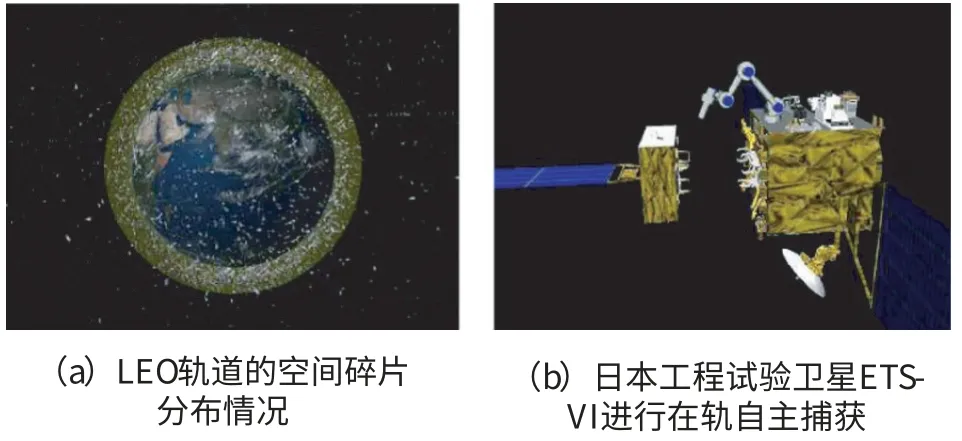
图1 空间碎片与在轨服务示意图Fig.1 Illustration of space debris and on-orbit servicing
综上所述,非合作目标运动参数估计对于抓捕任务甚至空间活动中都有着不可替代的重要性。
非合作目标的运动参数主要包括自旋运动参数:自旋轴方向、自旋角速度;章动运动参数:翻滚轴方向、章动角、章动角速率。对于本文研究的角速度估计,传统方法是将角速度求解问题转化为相对位姿关系的状态参数求解,已经相对成熟。很多学者在输入特征方面做出改进,Peng等使用双目立体匹配与激光雷达融合,在条件不满足三维重建时,直接使用激光雷达点云数据,经过点云融合、点云匹配最终使用扩展卡尔曼滤波(Extended Kalman Filter,EKF)状态估计得到目标的位置姿态参数、角速度与线速度估计值。Li等提出了一种基于连续点云的估计方案,使用EKF估计李群矩阵阵列,完成对目标结构、惯性参数的估计。Ge等使用立体视觉提取目标上三个不共线的特征点的位置矢量作为EKF输入估计,这样避免了估计目标观测坐标系与惯性主轴坐标系之间的四元数,可以直接估计目标的惯性主轴,但这是一个双线性问题,难以获得全局收敛。
相对于提高输入数据质量,另一种思路是在估计方法或者滤波器方面做出了改进,例如Peng还融合了EKF与无迹卡尔曼滤波(Unscented Kalman Filter,UKF)形成新的混合卡尔曼滤波器(Hybrid Kalman Filter,HKF),相比EKF提高了滤波器对于非线性的近似误差,相比UKF提高了迭代效率。Qiu等提出了角速度—惯性张量—运动参数的两步法,即先从四元数的微分伪逆求解出粗略的角速度,经过低通滤波与SVD降噪求解惯性张量,再利用EKF估计精确的运动参数,但是两步法在初始估计角速度就引入了相当大的误差,后续需要多次进行降噪,有可能对输入信息造成干扰。邢景仪等设计了基于方根高阶体积卡尔曼滤波器的估计方法。其选择五阶体积卡尔曼滤波与平方根滤波方法相结合的方法,以减少舍入误差对协方差矩阵正定性的影响,从而提高角速度估计的精度。邢还结合强跟踪的思想,设计了一种基于方差修正的无踪卡尔曼滤波的估计方法,实时修正滤波过程中的协方差矩阵,但其平滑性较差,计算复杂。
在上述以往提出的角速度估计方法都是使用滤波器的状态估计,精度很大程度上受到位姿估计结果误差干扰,同时滤波器还受到初值的较大影响,导致在高转速下需要较长的收敛时间,甚至不收敛。Wang等提出了一种基于立体视觉的非合作目标3D重建和状态估计的6D-ICP方法。将光流法应用于由金字塔KLT跟踪的Harris特征点,跨连续帧提取的每个单目相机中的目标图像特征跟踪,再匹配两个相机之间的同位特征,并生成相应的3D结构点,最后基于6D-ICP算法估计相对3D变换并重建目标3D点云,可以在10mm的精度跟踪目标的位移。范佳杰针对火箭箭体的几何特征,将其抽象为一个细长型圆柱体,使用激光雷达得到目标火箭的表面点云,根据圆柱体在自由翻滚运动中其自旋轴、翻滚轴、章动角之间的几何关系与欧拉动力学约束,依次求解得到目标的自旋轴、翻滚轴、章动角与章动角速率,但是由于各项参数直接依赖于上一步的输出,容易形成累计误差,在章动角7deg,章动角速率30deg/s,章动角速率误差已经达到4.2deg/s。Ivanov基于单目相机,根据Clohessy-Wiltshire运动方程,建立估计参数向量函数,再根据相邻帧之间的函数变化求解运动。由于其相邻帧之间只是简单的使用邻域关系,并没有用特征匹配,所以鲁棒性并不乐观。本文提出一种无需滤波器、基于目标运动与投影的观测关系的算法,其不依赖于位姿结果的微分关系。算法直接将非合作目标的序列帧作为输入,通过直线特征的全局跟踪,得到的投影点序列在信赖域算法的回归下,得到了高精度角速度。不同于Gu的基于投影角的方法,本文直接使用特征点,不再受到图像主点与三角函数奇异值的干扰,并且MSER为单特征,只要特征稍微有破坏,结果将失效。同时本文在原理上叙述更加完备,为后续研究提供了支撑。
2 投影几何法估计角速度计算
2.1 相关坐标系
如图2所示,本文涉及的坐标系主要有以下几种:
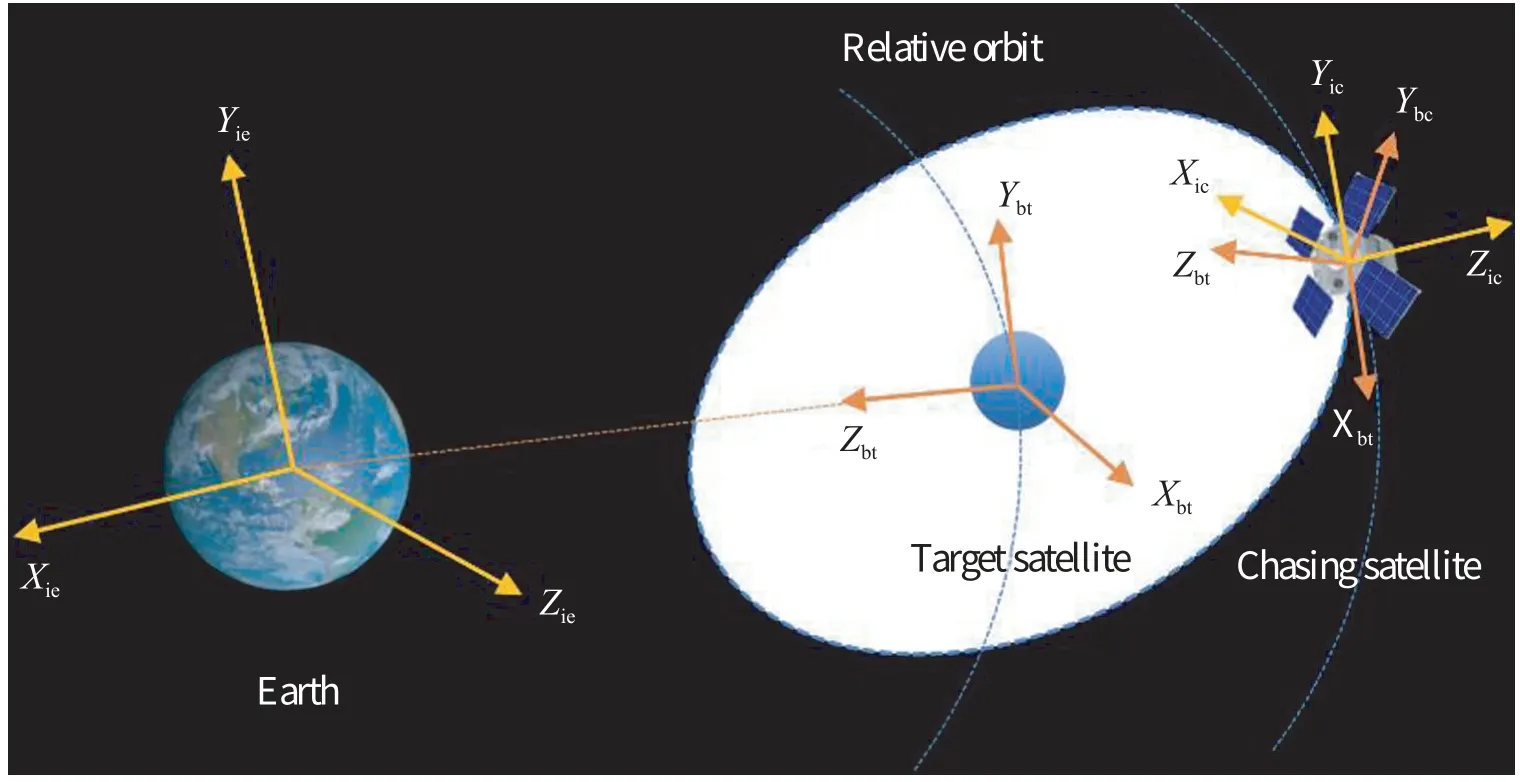
图2 空间坐标系示意图Fig.2 Illustration of the spatial coordinate systems
①惯性/空间参考系(Inertial Reference Frame,IRF):地心惯性坐标系,;服务卫星惯性坐标系,;视线/相机坐标系,,相机坐标系与惯性坐标系变换关系已知,故也可作为参考坐标系。
②固定坐标系/本体坐标系(Body Flame,BF):空间非合作目标本体坐标系和服务卫星本体坐标系。坐标原点选择为目标或是服务航天器的质心,三个坐标轴方向与各自的惯性主轴重合并且满足右手坐标系。
③其他坐标系:图像坐标系,,与相机坐标系关系已知。
2.2 投影几何估计法
本文提出一种新的投影几何法估计目标的角速度,通过图像坐标系上的投影点,直接获取目标角速度,如图3所示,相比滤波器的状态参数估计法基于位姿结果与运动关系求解角速度,投影几何解法避开了位姿关系的求解,且所需要的数据信息量更少。
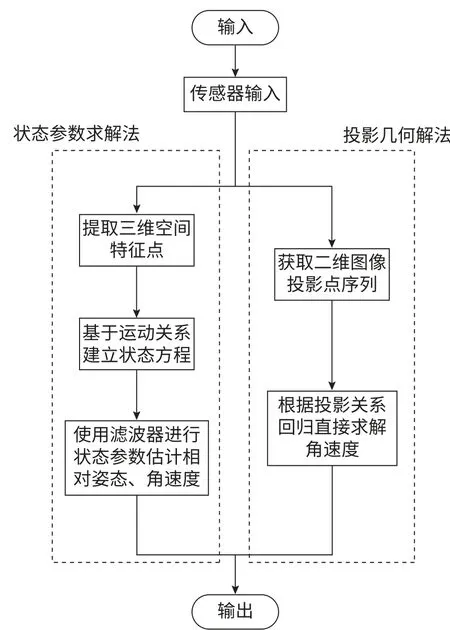
图3 方法对比Fig.3 Method comparison
(1)三维空间中非合作目标的角速度周期性
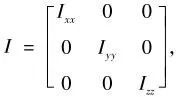
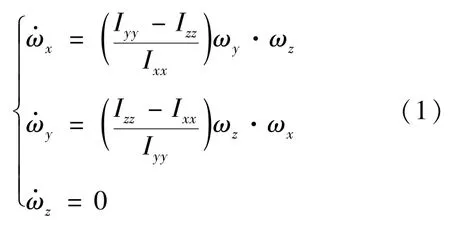
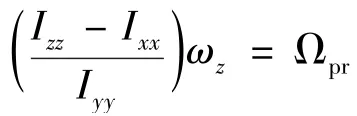
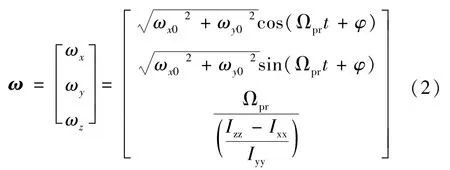
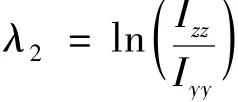
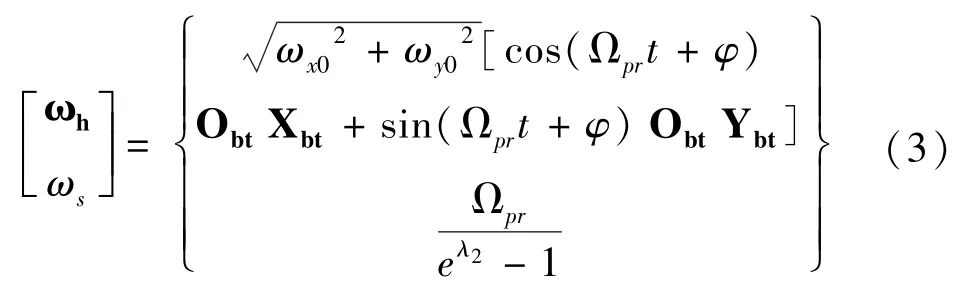
OX、OY为目标本体坐标系的轴向,根据简谐运动的定义,在惯性主轴、平面上,角速度的分量ω、ω满足简谐运动规律。
(2)小孔模型下轴向角速度的周期性
对于单轴自旋稳定目标,如图4所示,p是三维点p(x,y,z)投影在图像平面上的投影点,坐标记为(,)。
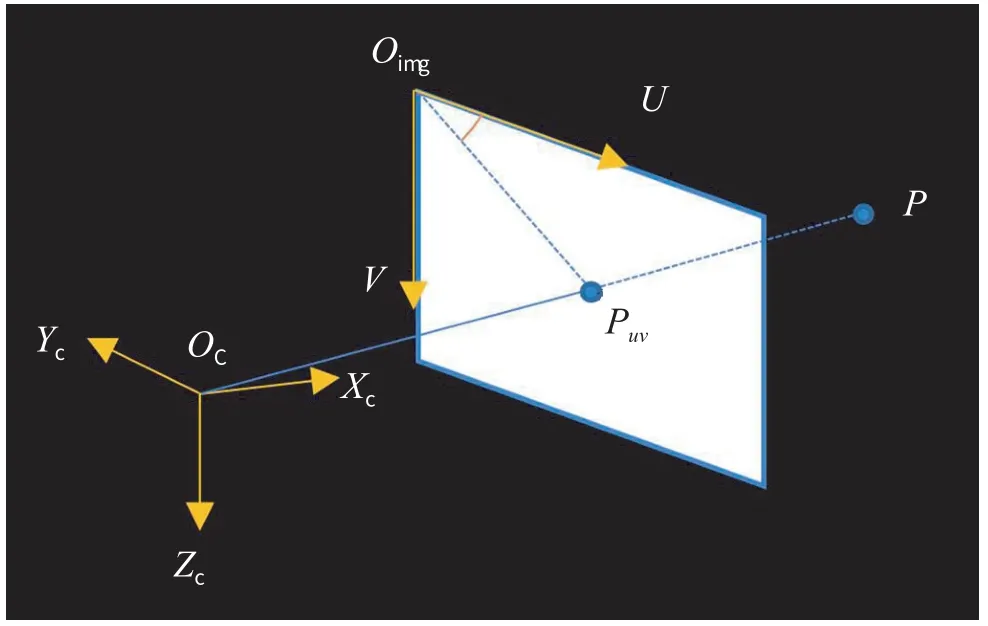
图4 投影点示意图Fig.4 Illustration of projection angle
根据相机的小孔模型有式(4)
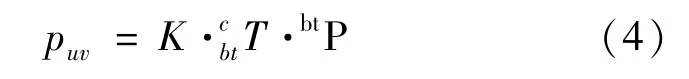
式中,、p为目标本体坐标系上的特征点与其在图像坐标下投影点的齐次坐标,为相机内参,
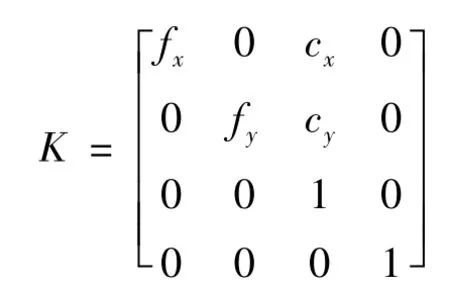
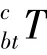
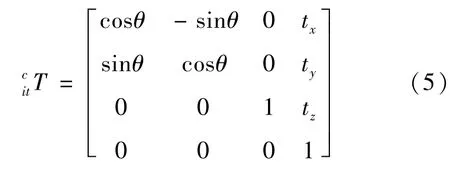
图像投影点满足
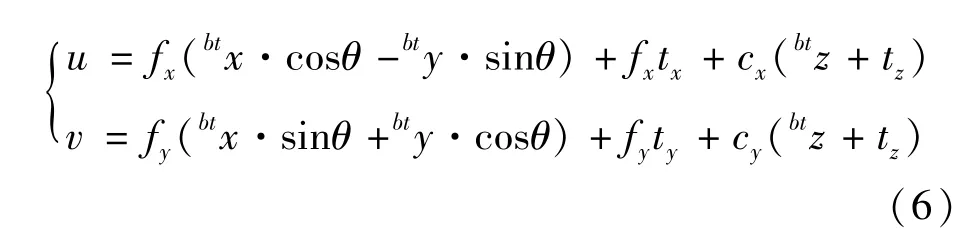
根据和差公式,d、d表示非含时项,投影点的简谐运动关系可表示为
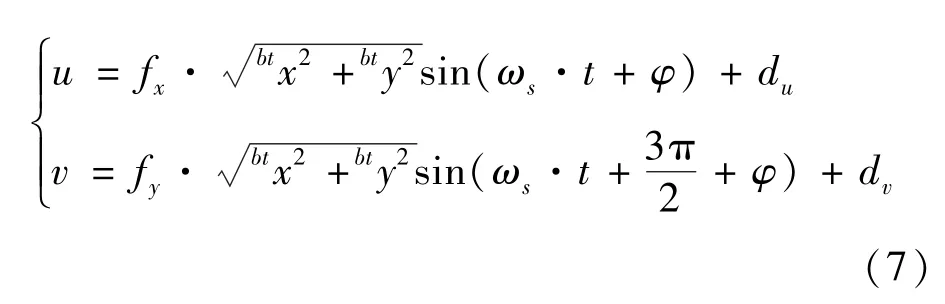
中的非合作目标投影点(,)依然符合简谐运动的基本规律且周期与轴向自旋角相同。本文将基于这一性质,在非合作目标单轴自旋状态下估计轴向角速度。
3 投影几何法中的图像算法设计
以上的投影几何估计法的关键就是对非合作目标在图像平面上的投影点进行跟踪。对于空间位姿求解,由于单目相机缺少深度信息,无法求解3D关系,但是对于角速度求解问题,单目相机足以满足求解所需要的信息维度。本文提出一种基于图片连续帧直线匹配的端点的跟踪方法以获取投影点。相比点特征其优势是:①直线特征更容易检测,尤其对于包括卫星在内的大多数人造物体,存在大量直线边缘特征,使用直线特征提取可以更大程度上利用目标的几何特性;②线特征具有更好的鲁棒性,受到光照、遮挡、视角变化的影响更小;③提供了更多信息(排序、拓扑结构等等),在特征数据维度上提高了上限。大量实验表明,由于卫星大多配备太阳能帆板,直线特征作为高频特征在卫星图像处理中的特征提取应用中有良好的效果。
本文中将使用直线段检测(Line Segment Detector,LSD)作为直线特征提取方法。相比于Hough变换直线检测,LSD直线特征拥有亚像素级检测精度,且为无需算法内参数调节,只需要设定放大倍数与高斯核大小即可通过这两个参数,控制误检直线的数量,将误检概率降到最低。特别是空间这样高噪声的环境,LSD拥有绝对的时间复杂度优势。
3.1 帧间直线匹配流程
本文直线匹配采用了直线段的长度、角度和中点位置作为匹配的标准,在Xu的基础上提出了一种根据邻域边进行匹配检验的连续帧直线段匹配算法,如图5所示。
1998年,我在写诗,并因此结识了几个写诗的朋友。那时候,互联网还是个新东西。两年之后,我所在的小城才开始出现第一个网吧。之后,那些疯疯癫癫的女孩子才开始用ICQ约会与聊天。
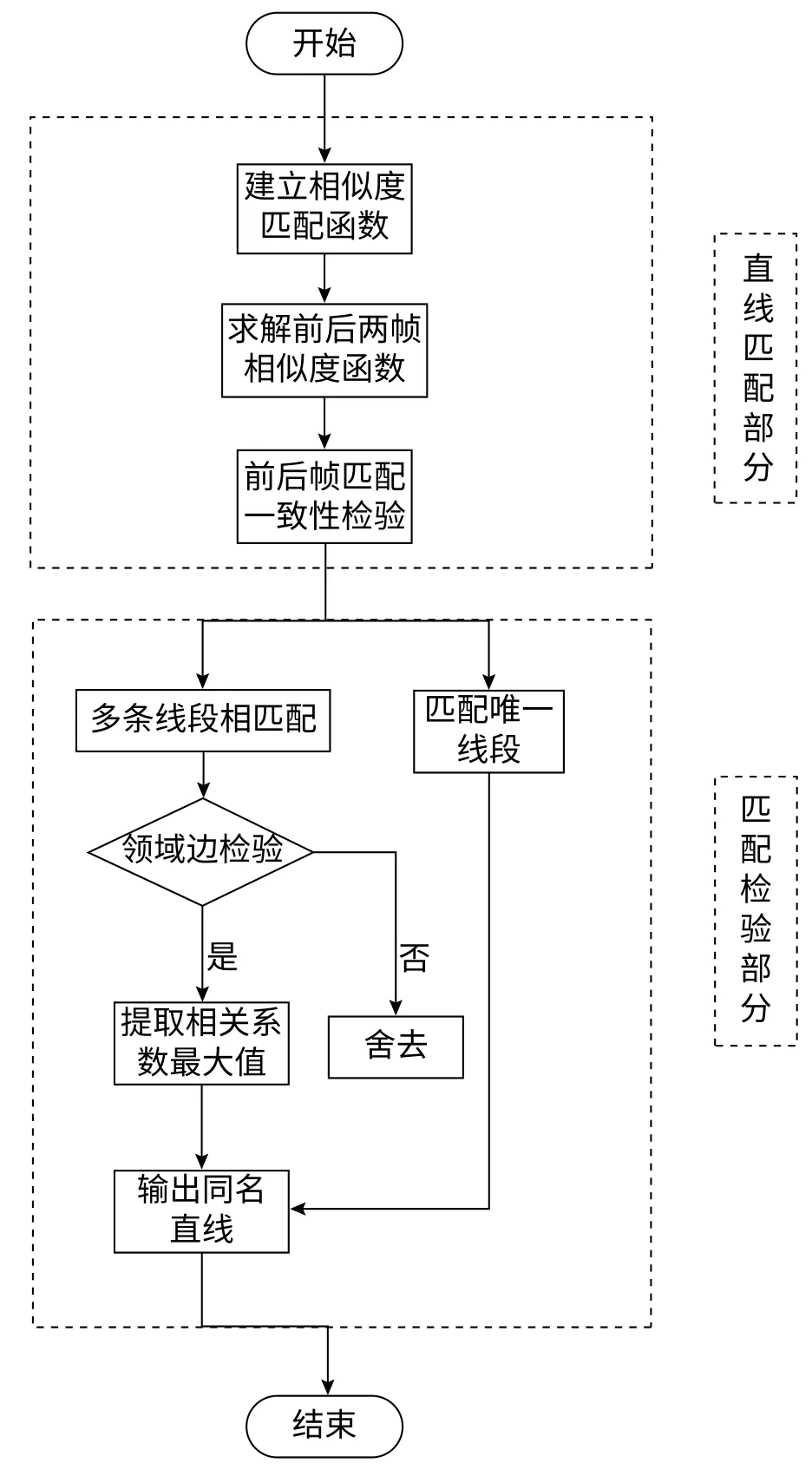
图5 图像连续帧匹配Fig.5 Image continuous frame matching
其中直线段的长度、方向和中点位置很好地描述了直线段自身的属性。直线段的长度、角度、中点位置均与二维笛卡尔坐标系下的直线几何性质定义一致。
直线段长度相似度函数
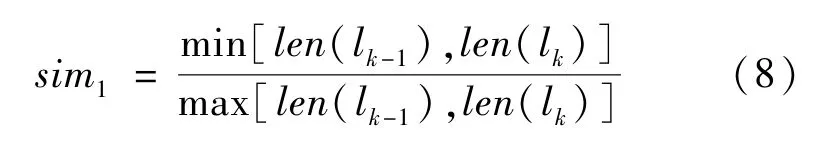
直线段角度相似度函数
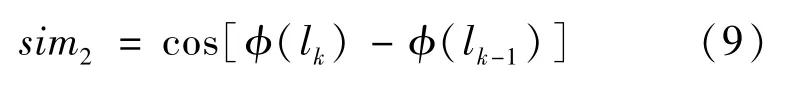
直线段中点相似度函数
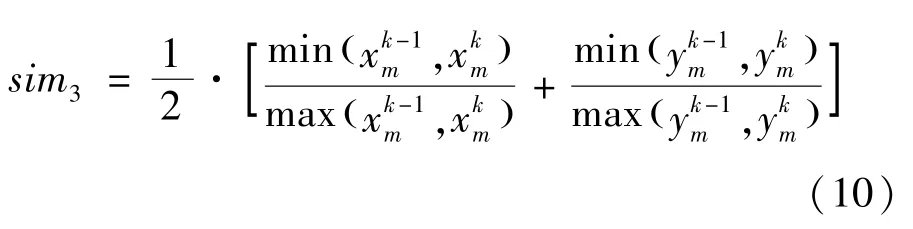
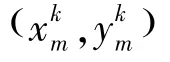
最后得直线段相似匹配函数
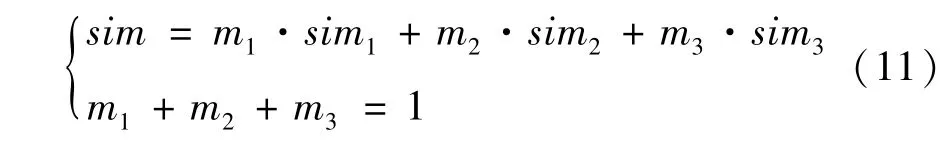

sim表示前一帧第条直线与后一帧第条直线的相似度。取超过阈值的直线对,将结果分为以下两种情况:①sim>ε且为列最大值也为行最大值,即前一帧关于第条直线在后一帧中的第条直线唯一匹配,直接输出同名直线匹配对。②存在个sim>ε,个sim>ε,均为行(列)最大值非行(列)最大值。此时本文使用一致性检测与领域边检验,剔除误匹配直线。
3.2 匹配检验流程
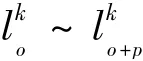
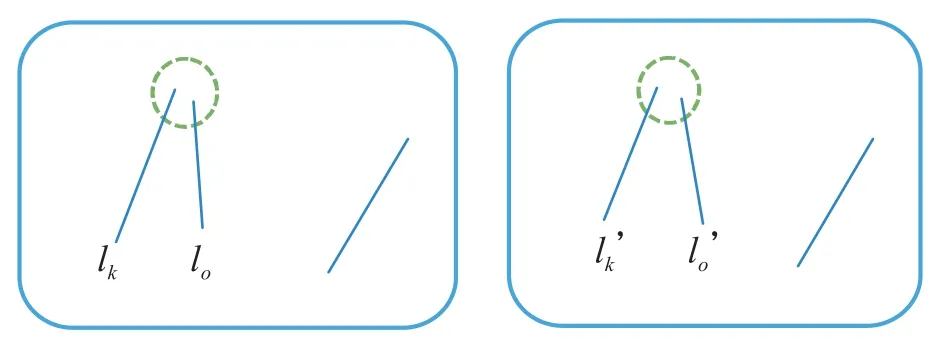
图6 邻域边检验示意图Fig.6 Illustration of neighborhood line test
通过调节LSD检测放大倍数与高斯核参数控制误检直线的数量和检测精度,通过调节阈值、控制匹配的准确度,得到如图7的匹配结果。将图7得到的匹配端点数据均值
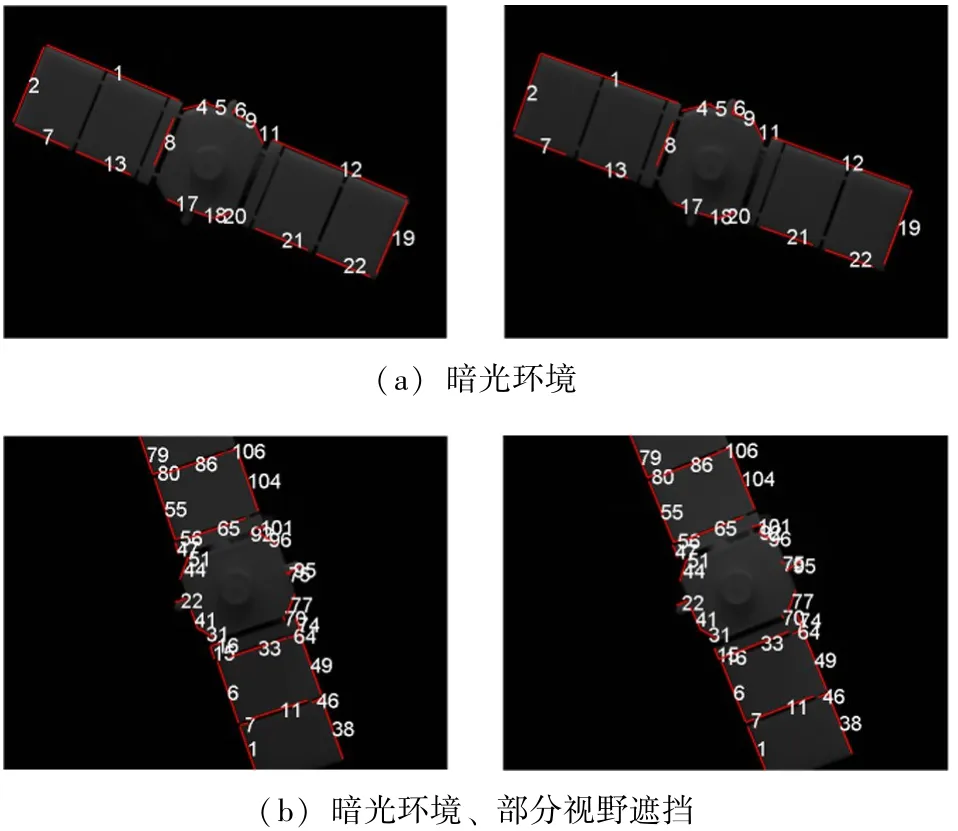
图7 匹配结果示意图Fig.7 Illustration of image matching
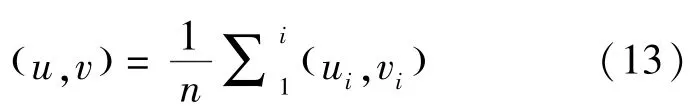
使用(,)·sin(·)对投影点进行回归,(,)为横、纵坐标,参数与距非合作目标距离、图片像素相关,参数与初始位姿相关,参数用于平衡图像主点与相机光心与非合作目标的几何中心,所得频率,在单轴自旋运动中即为自旋频率,即角度制角速度为
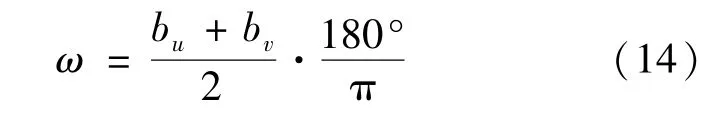
4 实验验证
本文在实际物理平台测量了的空间单轴自旋稳定状态的角速度。如图8所示,搭建了由计算机—单目相机、控制器—旋转台组成的运动估计实验平台。其拍摄测量的数据集如图9所示。图9中使用的卫星模型为NASA官网提供的SOHO卫星。对序列帧进行第二节的算法获取转动平台设置的角速度,使用计算机CPU为Intel(R)Core(TM)i5-1035G4,主频1.10GHz,内存8G。回归结果如图10所示。

图8 运动估计测量平台Fig.8 Motion estimation platform

图9 图像序列帧Fig.9 Illustration of image frame sequence
图10分别为相机采样频率1z下,使用信赖域算法在不同光照、不同初始位姿、角速度分别为2deg/s、5deg/s、13deg、17deg/s、21deg/s、30deg/s、45deg/s对投影点轨迹的单次回归结果。图中投影点(projection points)(,)为式结果,回归曲线(regression curve)为(,)·sin(·)所得,描述了特征点在图像坐标系下投影的运动关系。根据式求解得到估计结果见表1。其中绝对误差公式为
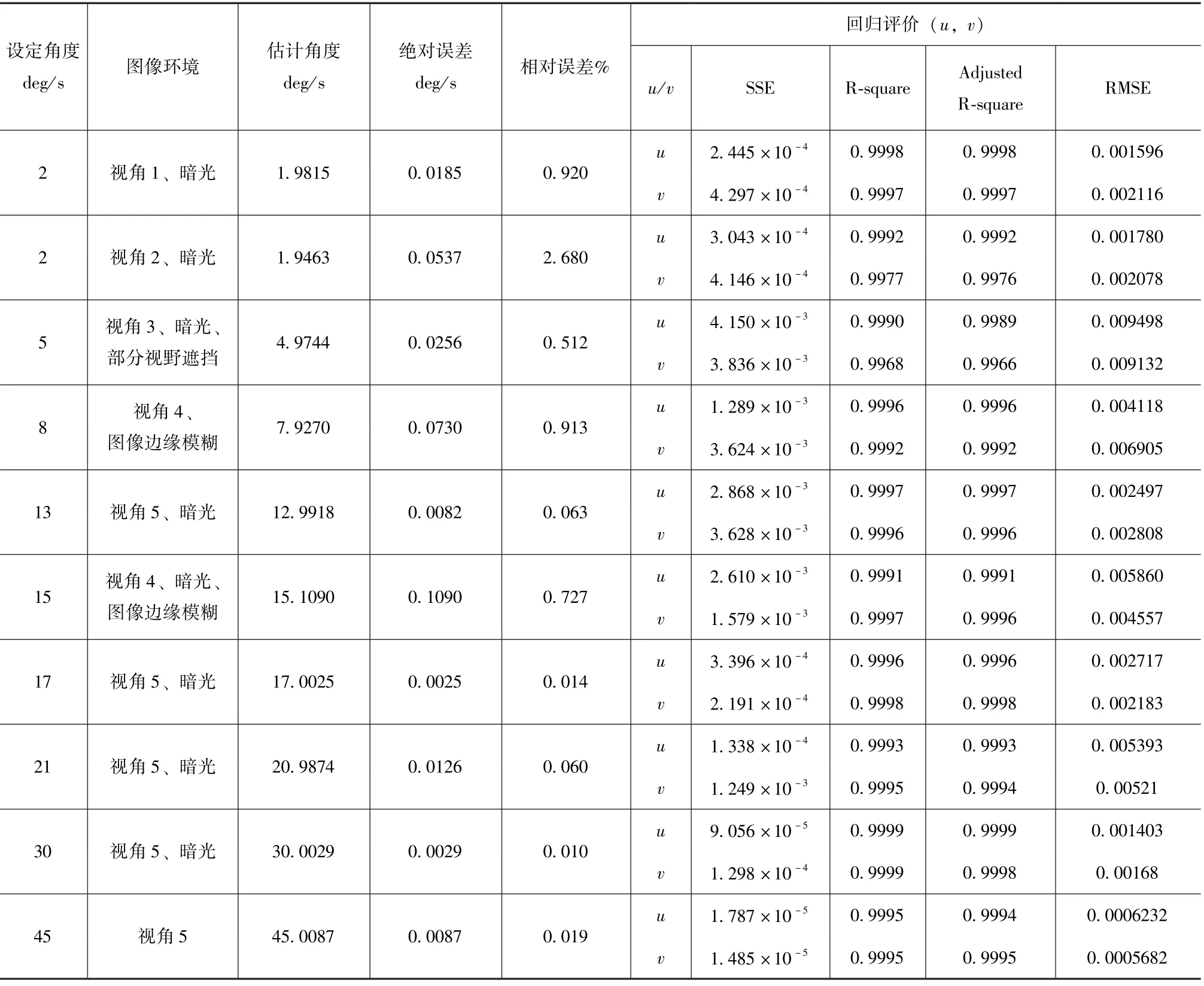
表1 误差与回归评价Table 1 Evaluation of error and regression
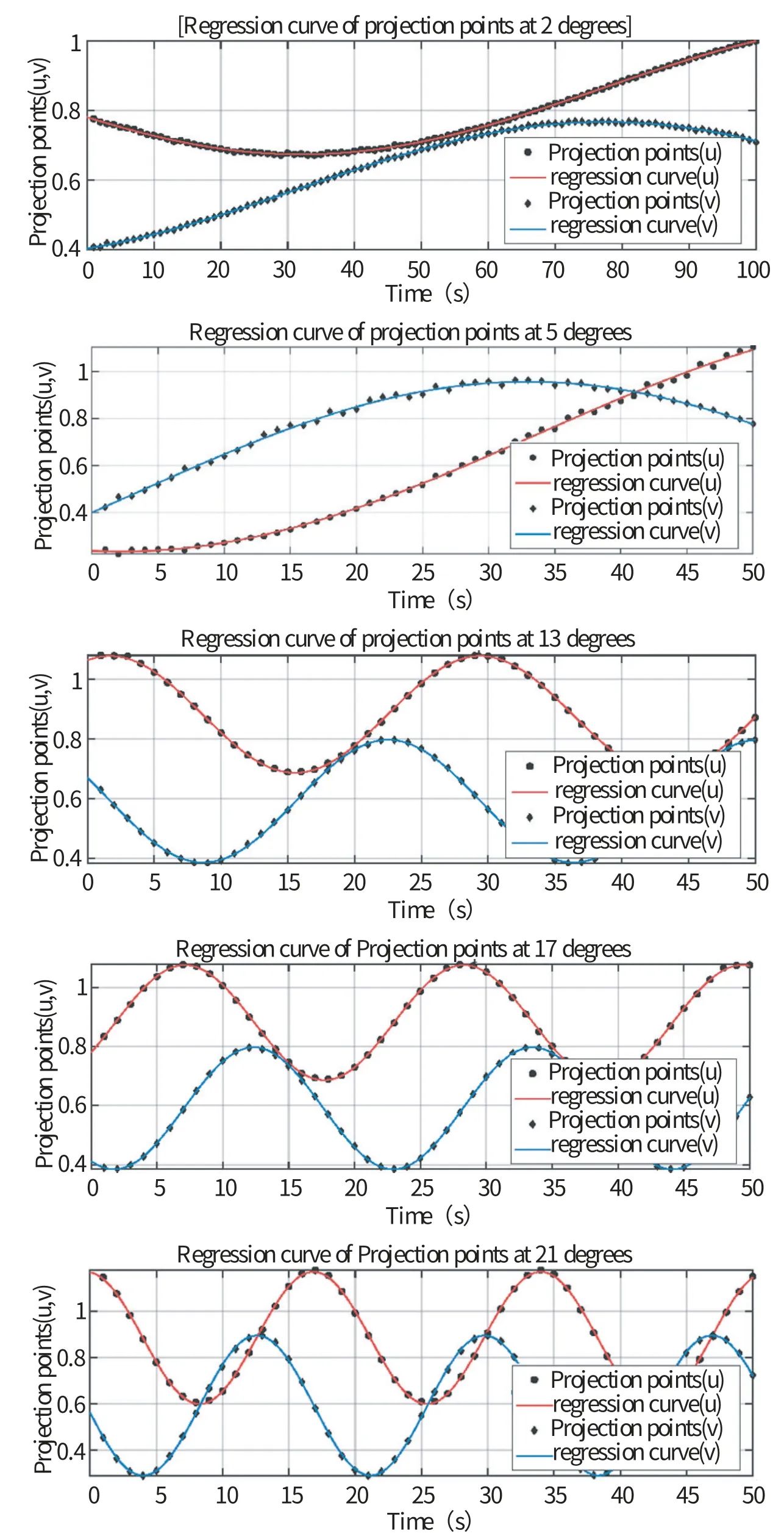
图10 投影点轨迹回归Fig.10 Projection point trajectory regression

相对误差公式为
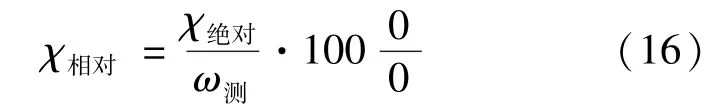
表示转台设定的角速度,表示算法输出的角速度。使用残差平方和(Sum of Squares due to Error,SSE)与均方根误差(Root Mean Squared Error,RMSE)评价信赖域算法回归的精度,用可决系数(R-square)与校正可决系数(Adjusted Rsquare)评价(,)·sin(·)关系的可靠性。
从实验结果中绝对误差与相对误差中可以发现误差并不随角度增加而增加,误差水平的决定因素是直线检测中的精度。而影响误差的主要因素有:图像获取时的图像质量、与相机的相对位姿以及相关参数设置的精确性。如8deg/s与15deg/s由于检测精度相对低,导致结果误差水平高于其他组。通过回归评价可以发现回归关系可靠性高、精度水平高。在帧间自旋角差,即大于60deg时需要提高采样频率以确保直线匹配的旋转不变性。
5 结论
对于空间非合作目标在单轴自旋稳定下的角速度求解问题,本文在欧拉运动学方程与小孔模型投影关系对图像平面的投影与三维运动关系详细的推导下,提出一种角速度估计方法,通过提取、跟踪帧间直线特征,获取与投影点周期,估计角速度,并且这种方法相比状态参数估计方法更加简单、直接由图像输入、无需已知目标的位姿信息,并且由于角速度估计结果方差与姿态结果独立,可作为角速度状态参数估计结果的参考修正值,本文由于实验条件限制,只在单轴自旋情况求取了角速度,后续研究将针对自由翻滚状态下估计三轴角速度。文中通过实体实验说明了该方法在单轴自旋稳定目标角速度估计的有效性。

