超高性能混凝土单轴受压力学性能试验研究及理论分析*

胡翱翔

（深圳职业技术学院 建筑工程学院，广东 深圳 518055）

超高性能混凝土（Ultra-High Performance Concrete，以下简称 UHPC）是近年来土木工程领域研究较多的土木工程新材料之一，具有抗压、抗拉强度高、韧性好、耐久性优良的特点．目前对于 UHPC基本力学性能指标取值、不同力学参数之间的转换关系、本构方程等，还没有形成统一的规范，尚需进一步研究．关于UHPC的受压力学性能，国内外学者进行了一定的研究．文献[1]研究了 RPC200的单轴受压力学性能．通过曲线拟合的方法建立了RPC200单轴受压本构方程．文献[2]研究了不同水胶比和纤维掺量对RPC单轴受压力学性能的影响．文献[3]研究了纤维掺量对RPC单轴受压性能的影响，钢纤维掺量变化范围为 1.03%～2.05%．根据试验结果基于曲线拟合的方法建立了RPC单轴受压本构方程．文献[4]研究了钢纤维掺量对 RPC棱柱体受压力学性能的影响，钢纤维变化范围为 0%～2%．文献[5]研究了不同钢纤维掺量对RPC材料单轴受压力学性能的影响，钢纤维掺量为1.5%～2.0%．结果表明：RPC轴心抗压强度与立方体抗压强度之间转换系数为0.8～0.9．文献[6]制作了300多组添加玄武岩纤维RPC棱柱体试件，建立不同配合比RPC单轴受压本构方程，研究了RPC抗压强度标准值和设计值的关系．由上可知，前人的研究主要集中在 RPC，对于纤维掺量较大的UHPC研究相对较少．并且研究人员大多是基于试验数据拟合的方法给出仅适用于各自试验的本构方程，并不具有普适性．基于此，本文设计制作6组不同钢纤维掺量的UHPC棱柱体单轴受压试件，建立不同受压力学参数之间的转换关系；结合国内外试验结果建立UHPC单轴受压损伤本构方程．

1 试验概况

1.1 试验准备

1.1.1 试验配合比

本文试验变量为钢纤维掺量，纤维体积掺量为0～5%，共6组试验，考察纤维体积掺量对UHPC材料单轴受压力学性能的影响，采用标准养护方式，试验配合比见表1．

表1 单轴受压试验UHPC材料配合比（kg/m3）

1.1.2 测试方案

试验在试件中心100 mm范围内安装位移计，测量试件在竖向荷载下的压缩变形，位移计位置如图1所示．

图1 单轴受压试验装置（单位：mm）

1.1.3 加载过程

试验加载过程按照位移控制．参考普通混凝土试验方法标准，先预加载，随后以0.05 mm/min加载速率从零加载至约300 kN，并持荷60 s；然后以0.05 mm/min速率卸载至0，重复3次，测量试件的弹性模量．第3次完成保持60 s操作之后不再卸载，继续按照0.01 mm/min的速度加载至试件破坏．

1.2 试件受力过程描述

图2所示为6组试件最终的破坏形态．将试件的破坏过程大致分为：弹性阶段、裂缝稳定发展阶段、裂缝非稳定发展阶段以及破坏阶段等 4个阶段．

1）弹性阶段．刚开始加载阶段 UHPC试件压应力较小，混凝土应变片数据较小，近似按比例增长，试件处于弹性受力阶段（σ≤ 0.6fc）；试件表面基本没有变化，没有出现可见裂缝．

图2 单轴受压试验试件最终破坏形态

2） 继续加大荷载，进入裂缝稳定发展阶段．当试件应力达σ≈ 0.8fc时，应变片数据增长速率明显加快，混凝土内部的微裂缝处于稳定开展阶段，试件表面仍无可见裂缝．

3）裂缝非稳定发展阶段．随着外荷载的增加，当试件应力达σ≈(0.8～1.0)fc时，应变加速增长，UHPC材料内部薄弱处的微裂缝开始传播并部分延伸至砂浆基体内部，裂缝开展进入非稳定发展阶段，并开始向试件表面延伸，试件表面可观察到少数可见裂缝．

4）破坏阶段．试件达到最大承载力，试件内部微观裂缝急剧扩展，内部界面裂缝相互连接并贯通，最终在试件表面形成宏观裂缝．峰值荷载过后，试验机发出“嘭”地一声巨响，试件被冲坏．试件表面出现宽度较大的宏观裂缝，试验加载过程结束．

2 试验结果与分析

2.1 试验结果

试验实测6组UHPC轴心受压试件的轴心抗压强度平均值、峰值压应变平均值、立方体抗压强度平均值、弹性模量平均值以及泊松比平均值等力学性能参数见表2．表中fc为轴心抗压强度；εc为峰值压应变；fcu为立方体抗压强度；Ec为受压弹性模量；υ为泊松比．

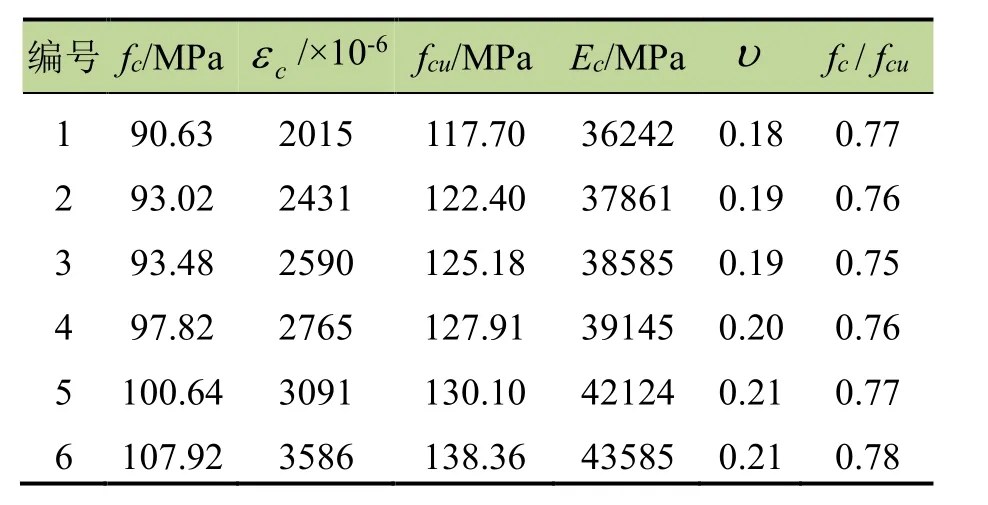
表2 UHPC单轴受压力学性能试验结果

2.2 纤维掺量对轴心抗压强度的影响

图3所示为纤维掺量对轴心抗压强度的影响曲线．从图中可知：纤维掺量从 1%增加至 5%，轴心抗压强度分别提高了2.6%、3.1%、7.9%、11.0%和19.1%，图3（b）所示；轴心抗压强度增长率分别为2.6%、0.5%、4.6%、2.9%和7.2%，增长率没有明显下降，也没有呈现出明显的规律，图3（c）所示．

图3 钢纤维体积掺量对轴心抗压强度的影响

2.3 纤维掺量对峰值应变的影响

图4所示为纤维掺量对峰值应变的影响曲线．由图可知：纤维掺量从1%逐渐增加至5%时，峰值应变分别增加了20.6%、28.5%、37.2%、53.4%和78.0%，如图4（b）所示；峰值应变增长率分别为20.6%、6.5%、6.8%、11.8%和16.0%，如图4（c）所示．

图4 纤维掺量对峰值应变的影响

2.4 静力受压弹性模量

图5所示为纤维掺量对UHPC弹性模量的影响．由图可知：纤维体积掺量从 1%逐渐增加至5%时，弹性模量分别增加了4%、6%、8%、16%和20%，纤维掺量从3%增加至4%时，弹性模量增长率最大．

图5 纤维掺量对弹性模量的影响

2.5 泊松比

图6所示为纤维掺量对泊松比的影响．由图可知：泊松比在0.18～0.21范围内变化，纤维掺量从0%增加至5%时，泊松比缓慢增加，增加幅度较小．

图6 纤维掺量对泊松比的影响

2.6 抗压力学性能指标取值

本文在试验基础上，收集整理UHPC轴心受压试验相关的国内外文献，建立了UHPC受压力学参数之间的转换关系．

2.6.1 轴心抗压强度与立方体抗压强度转换关系

收集、整理了国内不同研究机构[5,6,8-13]以及本课题组关于UHPC轴心受压试验数据，一共116组试验数据，如图7所示．采用线性函数模拟两者之间的关系，拟合曲线如图7所示．

图7 立方体抗压强度与轴心抗压强度关系拟合

2.6.2 弹性模量与立方体抗压强度转换关系

本文收集整理了国内有关UHPC轴心受压试验数据[1,6,8,10-12,14,17]，结合本文试验数据，一共收集了76组弹性模量与立方体抗压强度试验数据，它们之间的关系如图8所示．采用有理式方程拟合弹性模量与立方体抗压强度之间的转换关系，拟合公式为：

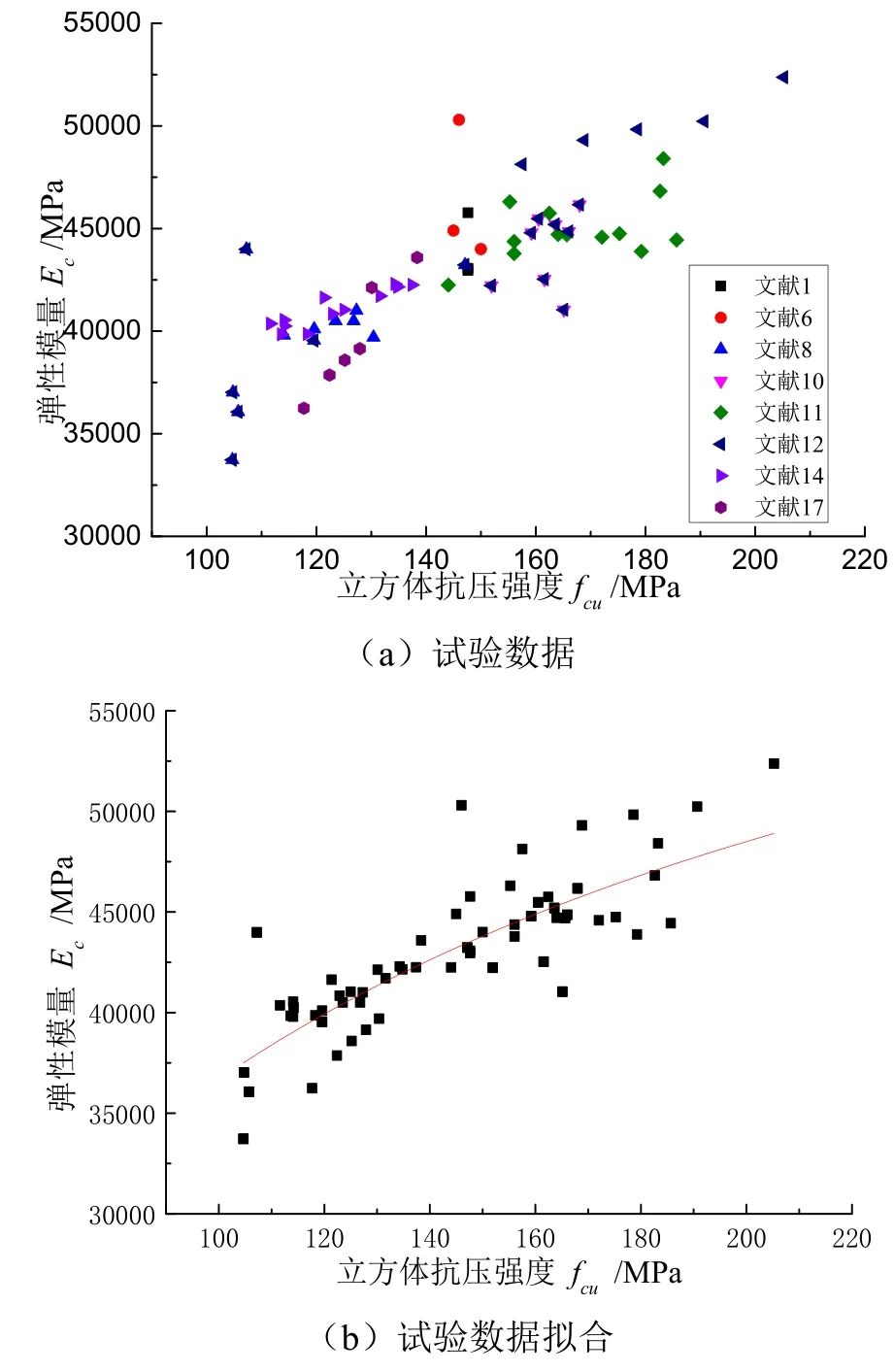
图8 弹性模量与立方体抗压强度的关系

上述拟合公式R2=0.66，弹性模量计算值与试验值之比的平均值为1.00，变异系数为0.05．

2.6.3 泊松比

由试验结果可知：单一型短纤维UHPC泊松比在0.18～0.21范围内变化，与纤维掺量相关．根据试验结果拟合公式如下：

拟合曲线如图9所示，R2=0.93．式中，v0=0.18为不掺纤维的泊松比试验值．

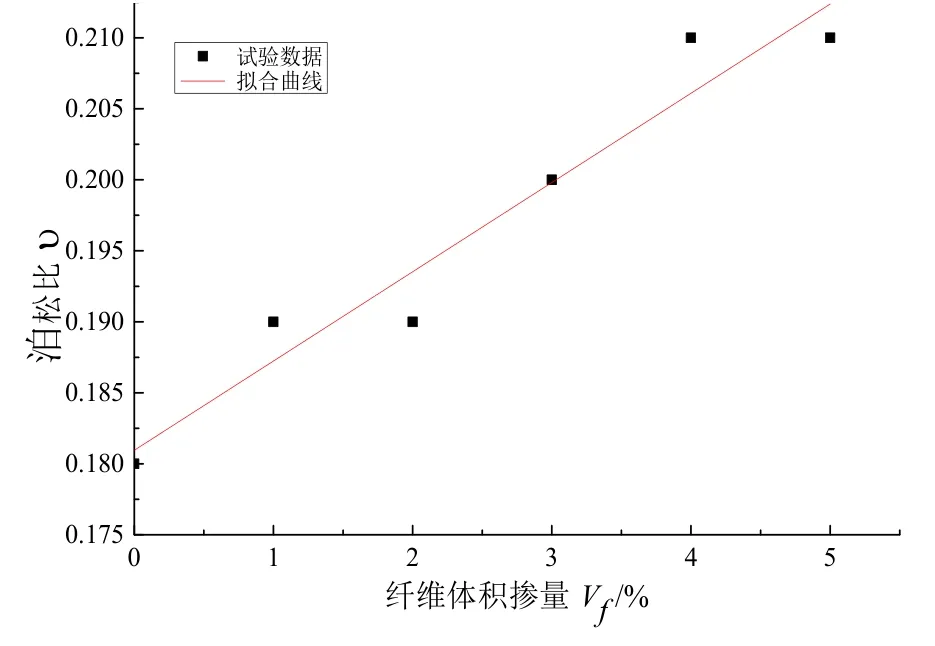
图9 泊松比与纤维掺量关系

3 单轴受压损伤本构方程

将上述表达式代入本构方程，即可得到UHPC单轴受压损伤本构方程．为验证上述方程的正确性，将计算结果与部分试验结果进行比较，如图10所示．可知：受压应力-应变曲线理论曲线与试验曲线吻合较好，可以很好地反映试验的全过程，故上述损伤本构方程是合理的．

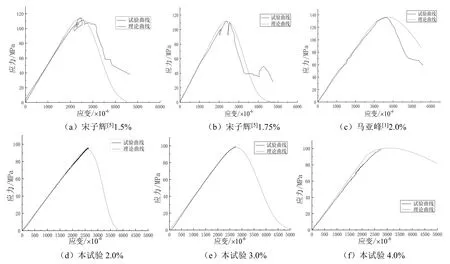
图10 受压应力-应变理论曲线与试验曲线对比

4 结 论

根据上述试验研究及理论分析得出如下结论：

1）掺单一型短细钢纤维 UHPC的轴心受压试验需附加一定的刚度辅助措施，才能保证获得完整的受压应力-应变曲线．

2）当短细钢纤维掺量不超过5%时，轴心抗压强度、峰值应变、弹性模量以及泊松比均随着纤维掺量的增加而增大．

3）建立了 UHPC材料的轴心抗压强度与立方体抗压强度、弹性模量与立方体抗压强度以及泊松比与纤维掺量之间的关系．

4）建立了考虑损伤阈值影响的受压应力-应变损伤本构方程，理论曲线与试验结果吻合较好．