应用二维相关近红外光谱特征建立蒙古栎弹性模量卷积神经网络预测模型1)
吕俊霄 陈金浩 张怡卓 王克奇
(东北林业大学,哈尔滨,150040)
蒙古栎(Quercusmongolica)是中国东北林区主要的次生林树种,其坚硬耐腐,常作为结构木材。抗弯弹性模量(MOE)是木材一项最重要和最具特征的力学性质,代表了木材力学性能的综合情况,也是实现木材分级的重要参数和依据[1]。传统的木材力学检测方法易造成浪费,且操作复杂,无法满足实际工程需要。近红外光谱是一种可靠无污染的分析方法,可对木材力学性质进行快速、准确地测定。Tong et al.[2]利用近红外光谱,建立了热改性南方松木弹性模量的偏最小二乘模型,横切面的预测决定系数为0.89;Shi et al.[3]使用近红外光谱结合PF-PLS模型对五角枫、桦树和柞栎的抗压强度进行预测,预测相关系数分别为0.89,0.92和0.90;Liang et al.[4]将近红外光谱与BP神经网络结合对蒙古栎弹性模量进行预测,预测相关系数为0.91。尽管近红外光谱具有快速、稳定、高效等特点,但在光谱特征提取过程中,仍存在检测到的信号微弱,大量的冗余信息使得光谱图不清晰等问题,从而影响建模精度。
二维相关谱将光谱信号扩展到第二维上,可以区分出在一维光谱上被覆盖的小峰和弱峰,从而提高了光谱的分辨率;通过谱线之间相关性的分析,可以详细地研究不同分子间或分子内的相互作用[5]。加入一定的外扰可以引起的光谱变化,进行相关分析得到二维同步相关谱和二维异步相关谱。通常二维同步相关谱表示频带强度变化的相对方向,二维异步相关谱表示频带强度变化的顺序[6]。虽然二维相关谱技术已广泛应用于食品检测[7]、环境科学[8]、生物学[9]等领域,但并未见二维相关谱预测木材力学性质的相关报道。
近年来,卷积神经网络(CNN)在光谱分析[10]、图像分类[11]、目标检测[12]和语音识别[13]等领域得到了广泛的应用。偏最小二乘法(PLS)方法多用于处理线性问题,BP神经网络易出现局部最优解现象。卷积神经网络可以隐性地从训练数据中进行网络学习,避免了手工提取特征过程导致误差累积的缺点,可通过权值共享减少需要训练的权值个数,降低了网络的计算复杂度;池化操作使得网络对输入的局部变换具有一定的不变性,提升了模型的泛化能力和鲁棒性。
本文以蒙古栎为研究对象,应用二维相关谱建立蒙古栎抗弯弹性模量卷积神经网络预测模型。首先对原始光谱进行多元散射校正、Savitzyk-Golay和一阶导数(MSC-SG-FD)预处理,使散射光的影响因素减弱,光谱的聚集度增强,且能够消除基线漂移和平缓背景的干扰以及高频噪声的影响,其次经二维相关分析得到二维同步相关谱和二维异步相关谱,最后将卷积神经网络与经MSC-SG-FD预处理后的二维同步相关谱进行建模,预测蒙古栎抗弯弹性模量(MOE)。
1 材料和方法
1.1 试验材料与数据采集
蒙古栎木材采自黑龙江省冲河林场,按照国家标准GB1927~1943—2009制取300 mm×20 mm×20 mm的抗弯力学试样,并挑选出无疵试样115条并编号,在进行光谱扫描后,完成力学性能破坏性测试得到相应真值。
实验室内进行近红外采集,室内温度保持在(20±1)℃,平均相对湿度保持50%。近红外光谱仪采用德国INSION公司生产的One-chip微型集成光纤光谱仪,波长范围900~1 900 nm,光谱分辨率<16 nm。采用两分叉光纤探头对试样进行径、弦面近红外光谱采集,每个切面均匀采集8个样点,每点扫描30次自动平均为1个光谱,记录保存。每个试样取径切面和弦切面的16组光谱平均成1条光谱。
采用木材万能力学试验机,参照国家标准《木材抗弯弹性模量测定方法》(GB1936.2—2009)测定蒙古栎木材的弹性模量。从115个蒙古栎样品中建立蒙古栎数据集,将全部样本随机划分为校正集和预测集,其中86个训练样本用于建立模型,另外29个预测样本用于检验模型预测性能。两样本集蒙古栎抗弯弹性模量测定结果如表1所示。

表1 蒙古栎校正集和预测集抗弯弹性模量的测定结果
1.2 二维相关谱理论
广义二维相关谱是对样本施加外部干扰,通过收集一系列光谱获得动态光谱,然后通过相关分析得到二维相关谱。动态光谱被定义为:
(1)
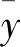
对于在等间隔t的m步长处测得的光谱,波长v处的动态光谱强度被表示为列向量y:
(2)
同步光谱强度(Φ(v1,v2))等于在(v1,v2)处动态光谱的向量积,表示为:
Φ(v1,v2)=[1/(m-1)]y(v1)T·y(v2)。
(3)
异步光谱强度ψ(v1,v2)等于(v1,v2)处动态光谱强度的Hilbert-Noda矩阵的向量积,表示为:
ψ(v1,v2)=[1/(m-1)]y(v1)T·N·y(v2)。
(4)
式中:N为Hilbert-Noda矩阵的第j行第k列的元素,表示为:
(5)
采集115个样本的近红外光谱,波长范围为907~1 864 nm。由公式(3)得到的原始二维同步相关谱(见图1),由公式(4)得出的原始二维异步相关谱(见图2)。
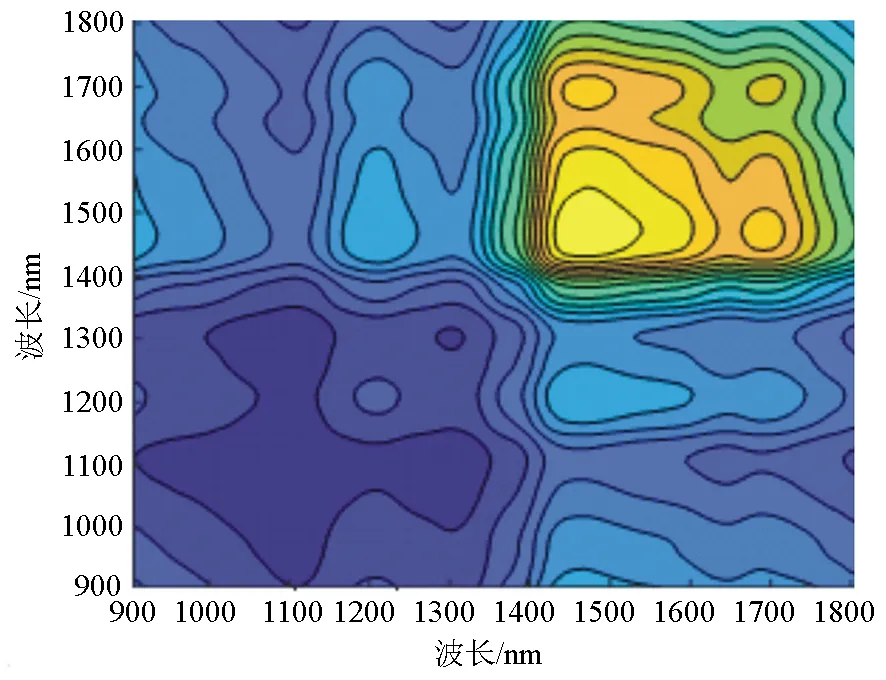
图1 原始二维同步相关谱
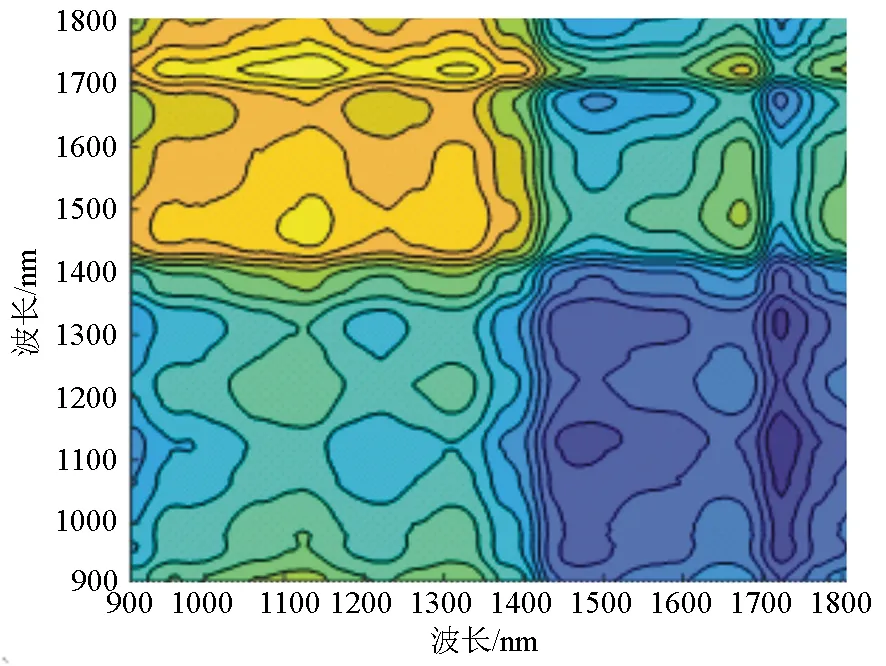
图2 原始二维异步相关谱
1.3 卷积神经网络
卷积神经网络(CNN)通常包括卷积层、池化层和全连接层。卷积神经网络可以通过卷积运算提取输入数据的不同特征。卷积计算公式为:
(6)

池化层又称下采样层,该层可以有效地减小参数矩阵的大小、参数的数量和模型的大小,提高计算速度,并提高特征数据的鲁棒性。线性整流函数(RELU)与其他激活函数相比,其具有更高的执行速度。线性整流函数保持激活的正区域,同时将所有负值转换为0。应用线性整流层后,池化层执行参数缩减以结合卷积层的特定特征,从而避免过度拟合确保稳定的卷积过程。
采用MATLAB R2019a建立卷积神经网络预测模型,利用样本数据对网络参数进行调整,具体模型参数设置见表2。两层卷积层卷积核大小均为2×2,数量为16,步长为1,扩充值为1;两层池化层采用平均池化方法,大小为2×2,步长为2;全连接层将输入数据从二维矩阵缩减为一维向量,并且识别输入数据中的特定特征,将其调整为输出层;输出层有一个神经元,用于实值回归。卷积神经网络模型结构见图3。

表2 CNN模型参数设置

图3 卷积神经网络模型结构
2 结果与分析
2.1 二维相关谱和光谱预处理
二维同步相关谱以对角线为对称轴,出现在对角线上的相关峰称为自相关峰,一般为正值,表示不同区域相关光谱变化的灵敏度;对角线两侧的峰称为交叉峰,交叉峰可正可负,表示不同波长上光谱信号的同步变化。若两个不同波长的峰同时增加或减少,则交叉峰为正,否则为负。
由图4可知,为解决原始光谱存在散射光、基线漂移和高频噪声等,分别采用MSC和MSC-SG-FD方法对原始光谱进行预处理。采用MSC对原始光谱进行预处理后(见图4(a)),散射光的影响因素减弱,光谱的聚集度增强,但同步谱图中的自相关峰和交叉峰仍不明显,信息强度依然较低。采用一阶导数结合SG平滑,不仅能够消除基线漂移和平缓背景的带来的干扰,而且可以抑制高频噪声。MSC-SG-FD对原始光谱进行预处理后(见图4(b)),与原始光谱相比,预处理后解决了散射光、平缓背景和高频噪声等问题,使自相关峰和交叉峰更加清晰。对角线上有2个较强的自相关峰,它们的位置分别在1 418 nm和1 691 nm处;7个较弱的自相关峰的位置分别在931、1 138、1 336、1 484、1 608、1 649、1 732 nm处,自相关峰表明了光谱强度动态涨落的程度;对角线两侧有7个正交叉峰和11个负交叉峰,交叉峰表明了不同波长上光谱信号的同步变化。
由图5可知,二维异步相关谱表示在v1和v2的光谱强度变化的差异,其不存在自相关峰。当v1和v2的光谱强度变化的相位不同时,就会产生交叉峰,可用来判断光谱强度变化的顺序。
经MSC-SG-FD预处理后的二维异步相关谱,交叉峰更清晰,具有更多的谱图信息。将二维同步相关谱与二维异步相关谱进行比较,不难看出同步相关谱的峰较清晰,且具有自相关峰,可提供更多的光谱特征。而异步相关谱较为复杂,易受到噪声等其他因素的影响。
由图6可知,不同预处理下的CNN模型预测集的真实值和预测值,二维同步相关谱与二维异步相关谱相比,经相同预处理方法的二维同步相关谱的真实值和预测值更为接近,预测效果更好;经MSC-SG-FD预处理后的二维同步相关谱预测精度最高。
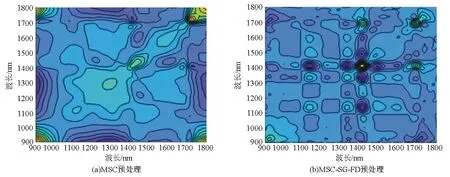
图4 不同预处理二维相关同步谱
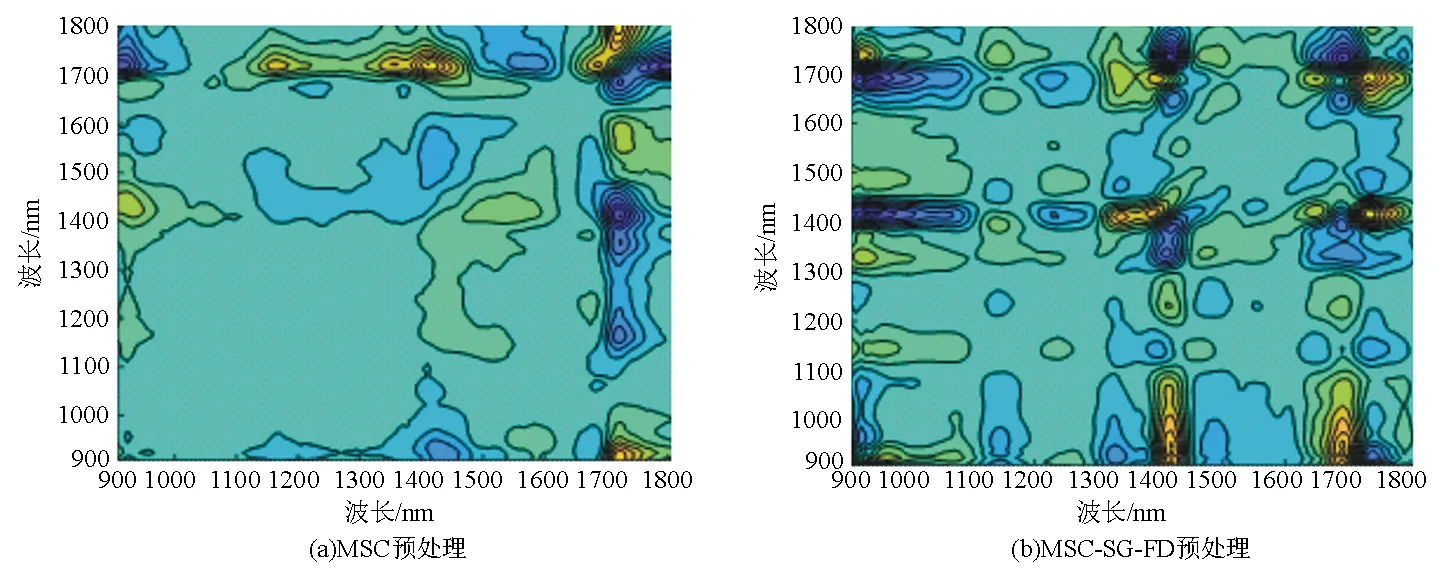
图5 不同预处理二维相关异步谱

(a)二维同步相关原始光谱;(b)二维异步相关原始光谱;(c)MSC处理的二维同步相关谱;(d)MSC处理的二维异步相关谱;(e)MSC-SG-FD处理的二维同步相关谱;(f)MSC-SG-FD处理的二维异步相关谱。
由表3可知,采用不同预处理方法的CNN模型预测蒙古栎抗弯弹性模量的结果,二维同步相关谱的建模效果均优于二维异步相关谱的建模效果。经MSC预处理后的二维相关谱建模效果优于原始的二维相关谱的建模效果;经MSC-SG-FD预处理后的二维同步相关谱建模效果最佳,校正集和预测集的决定系数分别为0.996 4和0.980 2,均方根误差分别为0.113 3和0.270 4。

表3 不同预处理下的CNN模型建立结果
2.2 预测模型分析
为验证CNN模型建模效果,分别建立了PLS模型和BP模型作为对比实验。PLS模型和BP神经网络运行环境均为MATLAB R2019a,输入均为经MSC-SG-FD预处理后的二维光谱矩阵,输出均为蒙古栎抗弯弹性模量的预测值。PLS模型采用全因子回归,主成分因子设置为10;BP神经网络设置为隐含层含有9个神经元的单隐层结构,最大迭代次数为1 000,目标误差为0.001,学习速率为0.01。对经MSC-SG-FD预处理后的二维同步相关谱进行建模,将3种模型的预测结果与真实值进行比较。
由图7可知,CNN模型与PLS模型和BP模型相比,CNN模型对蒙古栎木材弹性模量预测效果最佳,绝大部分样本均拥有很好的预测效果。

图7 3种模型预测值与真实值
由表4可知,3种模型预测集上的评价指标,PLS模型的预测性能较差,决定系数为0.805 6,均方根误差为0.874 8。因为PLS模型是一种线性模型,无法充分反映光谱与木材力学性质之间复杂的非线性关系;BP模型和PLS模型相比,其评价指标具有一定的提升,决定系数为0.920 7,均方根误差为0.477 9,但预测精度仍然不高;CNN模型的决定系数为0.980 2,均方根误差为0.270 4,在3种模型中预测精度最高。因此,利用CNN模型对蒙古栎木材弹性模量的预测效果优于传统的PLS和BP模型。
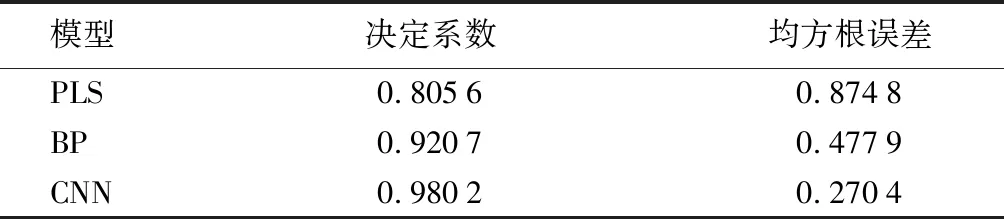
表4 不同模型对蒙古栎木材弹性模量预测的精度
3 结论
以蒙古栎样本为研究对象,将卷积神经网络用于二维相关谱预测蒙古栎木材弹性模量与原始二维相关谱和经MSC预处理后的二维相关谱相比,经MSC-SG-FD预处理后的二维相关谱建模效果最佳;二维同步相关谱与二维异步相关谱相比,二维同步相关谱更利于结合卷积神经网络对蒙古栎木材弹性模量进行预测;CNN模型可用于二维相关谱预测蒙古栎木材弹性模量,CNN模型与传统的PLS、BP模型相比具有最高的预测精度;CNN模型的建模方法可为预测木材力学弹性模量提供一种新思路。

