厚冲积层矿区地表移动持续时间预测方法研究

安士凯，李昱昊，王晓鹏，周大伟，安鱼飞，毕 波

(1.平安煤炭开采工程技术研究院有限责任公司 安徽省煤矿绿色低碳发展工程研究中心，安徽 淮南 232033；2.中国矿业大学 环境与测绘学院，江苏 徐州 221116；3.中煤航测遥感集团有限公司，陕西 西安 710199)

0 引 言

厚冲积层矿区在我国东部矿区分布较广，比如两淮矿区，兖州矿区，平顶山矿区等。厚冲积层矿区与一般矿区(无或薄冲积层矿区)相比，地表移动变形具有特殊性，如下沉系数大(甚至超过1.0)、边界角较小、下沉盆地边缘下沉曲线收敛缓慢、地表移动持续时间较长等地表移动特点[1-2]。针对厚冲积层沉陷的复杂性和特性，学者们从不同角度揭示了厚冲积层矿区地表下沉特殊性机理，吴侃等[3]通过相似材料模型实验系统，确定了厚表土层地区完备的地表沉陷预测模型；李文平等[4]从吸附结合水含量及其性质方面，论述了深部土体失水变形的机理与浅部已有认识的不同；王金庄等[5]提出采动程度衡量方法，揭示了厚松散层内部移动破坏机理；李永树[6]将复杂褶曲构造煤层划分为单斜构造煤层实行曲面积分，得到了单元下沉盆地和水平移动理论模型；刘义新等[7]模拟建立巨厚松散层下深部宽条开采数值模型，得出地表下沉系数的函数关系式；梁庆华等[8]从黏土体失水的角度，推导该情况下地表下沉的计算公式；周大伟[9]提出“分开-综合”的研究思路，揭示了厚冲积层岩土体的协同作用机理，构建了开采沉陷组合预测模型。但是现有资料对于厚冲积层矿区地表移动持续时间预测方法的研究较少。

煤炭井工开采引起的地表移动与变形是一个复杂的时间和空间问题。随着开采的推进，地表影响范围内某个点大致经历了开始阶段、活跃阶段和衰退阶段，在衰退阶段连续6个月累计地表下沉不超过30 mm，认为地表移动与变形稳定；这3个阶段所经历时间的总和称为地表移动持续时间。地表移动持续时间是评估地表移动与变形是否稳定的重要指标。随着东部矿区资源枯竭，部分矿井逐渐关闭，关闭矿井面临着诸多问题：如采煤塌陷地的治理、再利用，由矿方代理维护的国有设施的回收等[10]。政府回收土地再利用或设施回收的前提是地表或地面设施的稳定性评估。淮南老区关闭矿井后，由矿方代理维护的国有大坝及泵站等设施需移交给政府，政府接受之前要求，对这些大坝、设施的稳定性及闭井后续影响进行评估。因此精确预计地表移动持续时间对于地表及地面设施的稳定性评估至关重要。李德海[11]通过对实际岩移观测资料及Knothe时间函数的分析，得到了厚冲积层覆盖时覆岩岩性参数P的计算方法，基于时间影响参数C与P的关系，建立了时间影响参数C的精确计算方法；张广伟等[12]分析了岩石的物理力学性质、开采深度、开采范围和工作面尺寸与持续时间的关系，从下沉速度变化期移动时间入手推导地表移动总持续时间；郑志刚等[13]在厚松散层综放开采条件下，推导出开采深度、松散层厚度与地表移动时间之间的公式。综上，已有专家对此问题进行了研究，并获得有价值的成果。然而，依然缺少较合适的厚冲积层矿区地表移动持续时间的预计方法。笔者以淮南厚冲积层矿区实测地表移动持续时间为基础，分析了地表移动持续时间的影响因素，通过建模构建了一个更适用于厚冲积层矿区的的地表移动持续时间计算模型，并利用SBAS-InSAR监测数据进行对比验证。研究成果可在与淮南类似的厚冲积层矿区地表移动持续时间精确预计方面应用。

1 地表移动持续时间规范公式在厚冲积层矿区的适用性

20世纪50—60年代，我国有计划的在各矿区建立了地表移动观测站，积攒了大量的地表移动观测数据，建立了地表移动持续时间计算公式，并写入《建筑物、水体、铁路及主要井巷煤柱留设与压煤开采规范》(以下简称“三下规范”)，公式如下(H为平均采深，m;T为地表移动持续时间)：T=2.5H，H≤400 m；T=1 000exp(1-400/H)，H>400 m。“三下规范”是我国开采沉陷预测、煤矿开采地基稳定性评估等方面的指导性文件，上述公式在各矿区地表移动持续时间计算中具有重要作用；为了验证该计算方法在淮南潘谢新区的适用性，收集了15个潘谢新区实测值，见表1。利用该公式预计了该15个工作面的地表移动持续时间，预计结果与实测值对比，如图1所示。从图1可得，“三下规范”公式预计存一定的误差，其中最大误差为1 322 d(约3.6 a)，中误差约为959 d(约2.6 a)；该公式不适用于厚冲积层矿区，一方面是该公式考虑的影响因素较少(只考虑采深的影响)，另一方面是由于厚冲积层土体的特殊性导致。

表1 淮南潘谢新区实测地表移动持续时间Table 1 Measured duration of surface movement in Panxie New Area，Huainan

图1 实测数据与经验公式对比Fig.1 Comparison of measured data and empirical formulas

厚冲积层矿区地表移动持续时间具有特殊性。实测研究表明，与一般矿区相比，厚松散层矿区地表移动起始期更短，很快进入活跃期[14]，衰退期较长；地表移动初始期和活跃期占总移动时间比值较小，但占总下沉量的比值较大，而衰退期持续时间长，但下沉量较小[15-16]；如东庞矿实测起始期占总移动时间的6%，下沉量占总下沉量的2.7%，活跃期占总移动时间的37%，但下沉量却占总下沉量的95.3%，衰退期占总移动时间的57%，而下沉量只占总下沉量的2%。

2 地表移动持续时间影响因素

根据研究，地表移动持续时间的影响因素主要有：采深、采厚、推进速度、采煤方法及顶板管理方法、覆岩岩性(淮南厚冲积层矿区主要考虑厚冲积层土体的作用)[17-21]。将表1中15个实测数据中的平均采深、推进速度以及松散层厚度等分别与地表移动持续时间建立散点图，如图2—图5所示，分析各因素与地表移动持续时间的关系。

图2 平均采厚与地表移动持续时间的关系Fig.2 Relationship between average mining depth and duration of surface movement

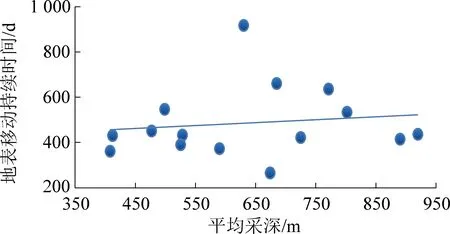
图3 平均采深与地表移动持续时间的关系Fig.3 Relationship between average mining depth and duration of surface movement

图4 推进速度与地表移动持续时间的关系Fig.4 Relationship between velocity of advance and duration of surface movement

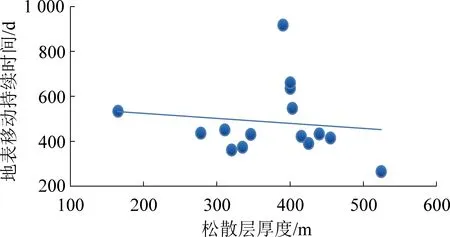
图5 松散层厚度与地表移动持续时间的关系Fig.5 Relationship between thickness of loose layer and duration of surface movement

由图2—图5可得：①采厚与地表移动持续时间程正相关。根据实测及已有研究表明：开采厚度越大，地表移动延续时间就越长。②平均采深与地表移动持续时间呈正相关。开采深度越大，地表移动时间越长，反之，开采深度越小，则地表移动时间越短。③推进速度与地表移动持续时间呈负相关。开采速度小，地表下沉缓慢，地表持续时间相对较长。④冲积层厚度与地表移动持续时间呈负相关。研究证实，岩性越硬地表移动持续时间越长，反之成立。冲积层土体在一定程度上使覆岩整体岩性弱化/软化，因此冲积层越厚，覆岩整体岩性越软，地表移动持续时间越短。

3 厚冲积层矿区地表移动持续时间计算模型建立

3.1 基于实测数据建模

计算得出地表移动持续时间：

(1)

3.2 计算精度分析

为验证所建模型的可行性和精确度，将表1中的实测数据代入计算，得出利用模型公式计算出的地表移动持续时间T1，与已知值进行对比。再使用“三下规范”中地表移动持续时间T的经验公式计算出地表移动持续时间T2，比较T1和T2两者的精确度。具体见图7和表2。

图7 修正模型和经验公式误差分布Fig.7 Error distribution of modified models and empirical formulas

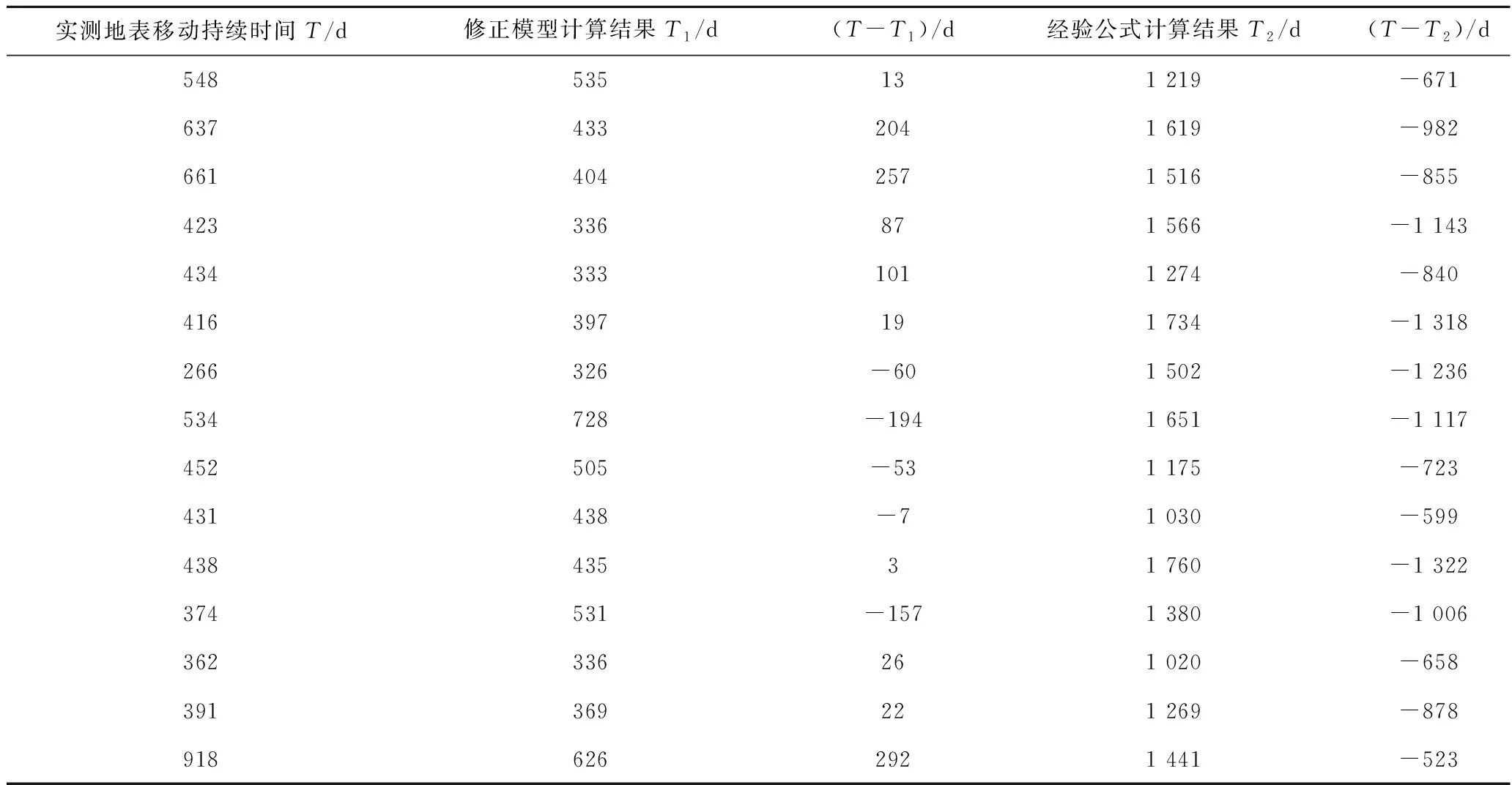
表2 地表移动持续时间计算模型与经验公式对比Table 2 Comparison between calculation model of surface movement duration

显然可见，图7建立的地表移动持续时间计算模型比“三下规范”中的经验公式更准确。由表2可知，修正模型计算结果中误差为137 d，而经验公式计算结果中误差为959 d，修正模型的计算精度相对于经验公式的精度提高了86%左右，在厚冲积层矿区适用性较好。

以上实测数据均用于建立地表移动持续时间计算模型，为了更充分的验证新建模型，收集其他未参与建模的厚冲积层矿区实测数据进行对比分析，结果见表3和图8。

表3 地表移动持续时间计算模型可靠性验证Table 3 Reliability verification of the calculation model of surface moving duration

图8 修正模型和经验公式误差分布Fig.8 Error distribution of modified models and empirical formula

由表3和图8可知，采用未参与建模的实测数据，代入修正模型中计算出的地表移动持续时间的精度仍然比经验公式的精度要高：新建模型的预计中误差为462 d，经验公式的预计中误差为818 d，新建模型的预计精度提高了约44%。相较之下，新建模型更适合厚冲积层矿区地表移动持续时间的预测工作，预计结果优于“三下规范”中的经验公式。

4 基于SBAS-InSAR的实测验证

合成孔径雷达干涉测量(InSAR)是近年来兴起的一种新型空间对地观测技术，具有全天候、无接触、大面积、高空间分辨率、高精度(厘米至毫米级)的特点，尤其在高精度的地表形变监测中应用广泛。实践研究表明，InSAR在矿区快速大变形监测误差较大，而其在矿区地表缓慢沉降的监测精度可达到毫米级别[22-23]。根据淮南地区的地表特点，采用SBAS-InSAR方法对地表移动进行监测。

4.1 实验区与实验数据

1)实验区概况。淮南矿区潘谢新区位于淮河以北，由厚冲积层覆盖，厚度一般在300～500 m，基岩相对较薄。实验区选取顾桥矿西南13-1煤层1211(3)工作面，该工作面平均采深550 m，冲积层厚度约为300 m，开采速度约为5 m/d，平均采厚为5.5 m，工作面的长度1 600 m，宽度为250 m，开采时间为2014年11月。采用综合机械化采煤方式。

2)数据源情况。本次地表形变解译采用的是SARscape软件，星轨道数据为欧空局提供的DORIS精密轨道数据，DEM采用CIAT机构分发的SRTM3V4 DEM。试验所用的SAR数据为2016-05-13—2018-12-17共26景Sentinel-1单视复数降轨数据，VV极化方式。

3)SBAS-InSAR数据处理流程。数据处理过程中参数设置如下：①干涉处理过程中距离向与方位向的视数比设置为4:1，滤波方法选用自适应滤波法，解缠方法采用最小费用流法，解缠相干性阈值设置为0.2。②选择没有残余地形条纹，远离形变区域的控制点，采用三次多项式模型进行轨道精炼和重去平。③其他参数均选用SARscape处理Sentinel-1数据的推荐参数[24]。

4.2 试验结果分析

在研究区中选取4个像素点(图9)，命名ABCD，绘制其沉降序列图，进行时间序列分析，沉降序列图如图10所示。

图9 研究的像素点与工作面的对应关系Fig.9 Relation ship between pixel and working face

图10 线段点位置示意及其时间序列沉降Fig.10 Line point position schematic and time series settlement profiles

由图11得到，当工作面推进到B点时，工作面前方1号点受到采动影响开始移动，推进到C点时，前方2号点受到采动影响开始移动，这种在工作面推进过程中，工作面前方的地表受采动影响开始移动的现象称为超前影响，开始移动的点到工作面的水平距离为超前影响距。通过计算1211(3)工作面的超前影响距，结合推进速度可知：当工作面推进至图9中1号点时，工作面前方A点开始受采动影响而下沉，当工作面推进至A点时，B点开始下沉，以此类推。

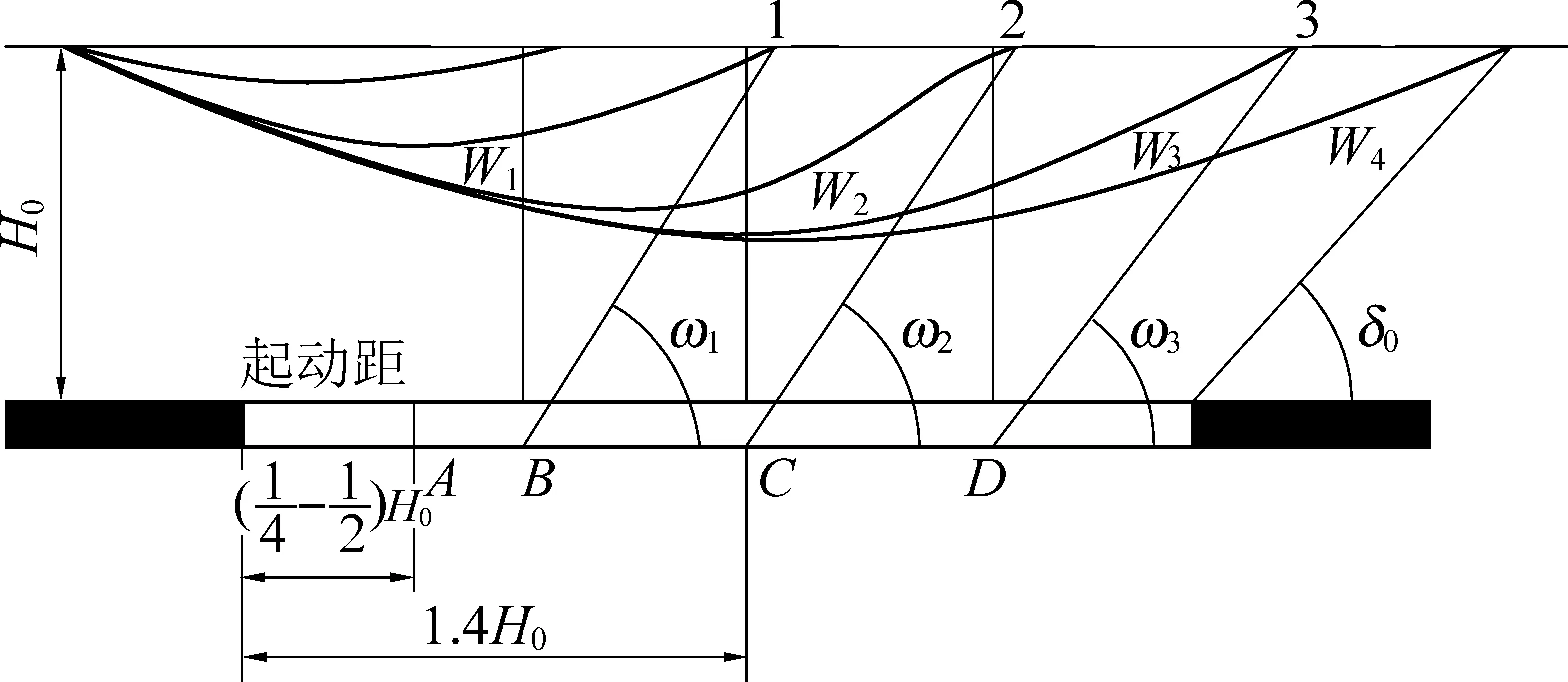
H0—平均采深；ω—超前影响角；W—下沉曲线；δ0—走向边界角图11 工作面推进过程中的超前影响Fig.11 Advance influence in advancing process of working face

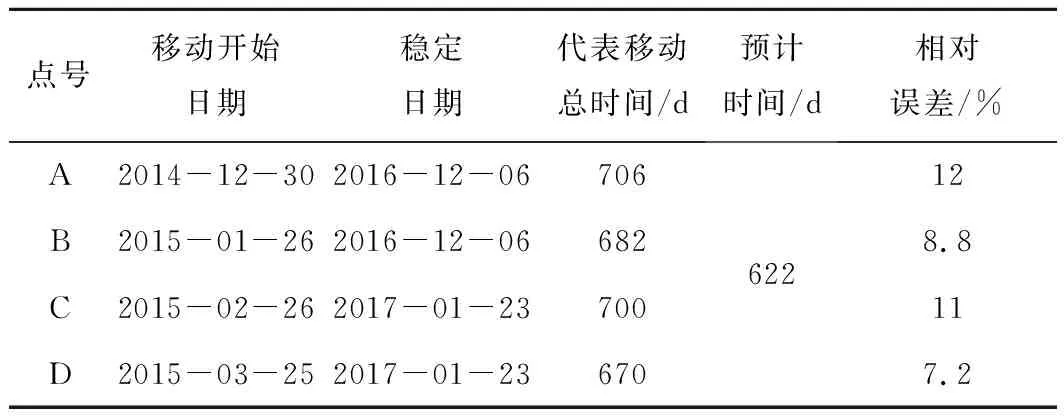
表4 淮南顾桥矿区1211(3)工作面地表监测点的地表移动持续时间Table 4 Surface movement duration of No.1211(3) working facein Guqiao Mining Area of Huainan

结合图9和图10，以D点为例，地表点D从2015年3月25日开始移动，从图10可知，在2016-07-24—2017-01-23的时间内，该地表点下沉量小于30 mm，根据地表移动持续时间定义：地表连续6个月下沉不超过30 mm，认为地表沉陷稳定。因此，该点于2017年1月份已经稳定，2015年3月至2017年1月，该地表的移动持续时间为670 d，根据新建地表移动持续时间计算模型(式(2))计算得到该地表点移动持续时间为622 d，相对误差为7.2%，二者基本一致。以此分析A、B、C三点，地表移动持续时间实测值见表，相对误差分别为12%、8.8%和11%。而用“三下规范”公式计算该地表点移动持续时间为1 309 d，误差最大的点是D点，最大相对误差为95.4%。再次证实了新建计算方法的正确性。

5 结 论

1)基于地表移动持续时间实测数据，由于现有地表移动持续时间计算公式考虑的影响因素较少(只考虑采深的影响)和厚冲积层土体的特殊性，导致其在厚冲积层矿区预计误差较大：预计中误差约为959 d(约2.6 a)，现有公式不适用于厚冲积层矿区。针对该问题，综合考虑了采深、采厚、冲积层厚度(覆岩综合岩性)和推进速度等地表移动时间影响因素，基于淮南潘谢新区15个工作面的实测数据，分析了各影响因素与地表移动持续时间的关系；并建立了厚冲积层矿区地表移动持续时间新的计算模型。

2)基于实测数据，采用参与建模的数据进行预计计算，得到新模型预计中误差为137 d，而经验公式计算中误差为959 d，新模型的精度提高了86%；采用未参与建模的数据进行预计，得到新建模型预计中误差为462 d，经验公式预计中误差为818 d，新建模型的精度提高了约44%。

3)采用SBAS-InSAR技术，利用Sentinel-1数据解算了淮南潘谢新区顾桥矿的1211(3)工作面地表的移动持续时间为670 d，利用新建模型计算得到地表点移动持续时间为622 d，相对误差最小为7.2%，二者基本一致，再次证实了该计算方法的正确性。对比传统经验公式，新建模型适用性更强，精度更高，为厚冲积层矿区采动地基稳定性评价等相关工作提供技术参考。