裂缝性多孔介质纵波频变特性研究
张金伟 丁仁伟 林年添 赵俐红
(山东科技大学地球科学与工程学院,山东青岛 266590)
0 引言
在饱和流体介质中,地震波发生频散和衰减的机制有多种,如地震波诱导流体流动[1-4]、地震波散射[5-6]、热弹性效应及相变等。其中,对前两种机制的研究最广泛[7-9],而第一种机制与储层孔隙结构、流体性质以及渗流特征密切相关[10]。
近些年,关于各向异性介质地震波频散和衰减的研究越来越多,在理论[11-12]和实验[13-14]两方面都取得了极大进展。在裂缝性孔隙介质中,当地震波通过裂缝时会挤压裂缝,并产生局部的压力梯度[15-16],为了平衡该压力梯度,黏弹性流体发生流动——地震波诱导流体流动。流体流动并不是瞬时完成的,需要一定的时间(松弛时间)重新达到压力平衡,因此地震波传播具有频变特性。松弛时间的倒数(特征频率)决定了地震波随频率发生频散(或衰减)的频率范围,并将频变特性分为低频特性和高频特性。当地震波频率较低时,孔隙流体有足够多的时间发生流动而达到平衡,因此孔隙空间(孔隙和裂缝)呈柔性特征,称为“松弛”状态; 当地震波频率较高时,孔隙流体没有时间发生流动,被“困在”孔隙空间内,称为“非松弛状态”,可将裂缝视为孔隙背景介质中的孤立裂缝。因此,在低频极限和高频极限时,地震波不发生频散和衰减,而在中间频带,压力得到部分平衡,地震波产生频散和衰减。当介质中只有孔隙时,特征频率与微观的松弛时间有关; 当介质中存在中观尺度裂缝(远大于孔隙尺度,但远小于波长)时,存在两种尺度的流体流动,对应两个松弛时间(特征频率),即与孔隙有关的微观松弛时间和与裂缝相关的中观松弛时间。这两种尺度的流体流动共同导致地震波的频散和衰减。微观尺度的流体流动往往发生在超声波频带,而中观尺度的流体流动一般发生在地震频带[17]。
基于Biot黏弹性理论和喷射流理论,Chapman[3]讨论了孔隙和微裂缝之间的流体流动,并引入一组定向排列的中观尺度裂缝,将其扩展为横向各向同性(TI)介质中的喷射流模型。大多数各向异性介质地震波衰减的研究只针对TI介质,即包含一组垂向裂缝[18]。实际上,由于成岩作用和地层压力等因素,储层中往往存在多组正交或斜交裂缝[19],因此研究含多组裂缝储层的地震波频散和衰减非常必要。Chapman[20]建立了包含两组裂缝的中观尺度喷射流模型,但是没有讨论两组裂缝对特征频率、频散和衰减幅度的影响。Chapman模型本质上是基于叠加理论的一阶近似模型,因此启发人们利用黏弹性模型表征Chapman模型,并将其扩展为包含多组裂缝的情况。
本文首先对Chapman模型数值模拟,讨论裂缝参数对特征频率和频散、衰减幅度的作用,然后分析Chapman模型和标准线性固体模型之间的关系,最后建立利用广义标准线性固体模型计算包含多组裂缝储层的频变纵波模量的方法。该方法利用低频、高频极限模量和模量损失表征地震波的频散和衰减特性,其中模量损失可表征每组裂缝的贡献。同时给出了低频、高频极限模量的计算方法。本文旨在提出一种简便、可行的方法,分析含多组不同长度和方向裂缝储层的纵波频变特性,并为处理复杂裂缝储层提供一个实用的岩石物理模型。
1 Chapman模型
Chapman模型的孔隙空间包括球状孔隙、硬币状微裂缝和硬币状中观尺度裂缝。其中:微裂缝的尺度与孔隙相同; 中观尺度裂缝的尺度远大于孔隙,而小于地震波波长。孔隙及微裂缝呈随机分布,裂缝定向排列,实际应用时一般忽略微裂缝的作用。Chapman模型中最重要的参数是流体的松弛时间。流体流动发生在两个尺度上,因此存在两个松弛时间:微观尺度松弛时间τm,与孔隙结构等有关,一般由实验室测定; 中观尺度松弛时间τf,不仅与孔隙结构相关,还与裂缝参数相关
(1)
式中:r为裂缝半径;ζ是颗粒尺度(孔隙尺度)。由式(1)可以看出,τf与r成正比。当r增加时(假设裂缝密度和裂缝纵横比保持不变),比表面积减小,必须有更多的流体通过单位表面积以平衡压力,因此需要更多的时间[21]。根据Chapman裂缝模型,包含两组定向排列裂缝的孔隙介质的频变刚度矩阵为
(2)
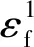
2 裂缝参数对纵波衰减的作用
2.1 裂缝方向对地震波的作用
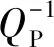
2.2 地震波入射方向的影响
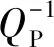
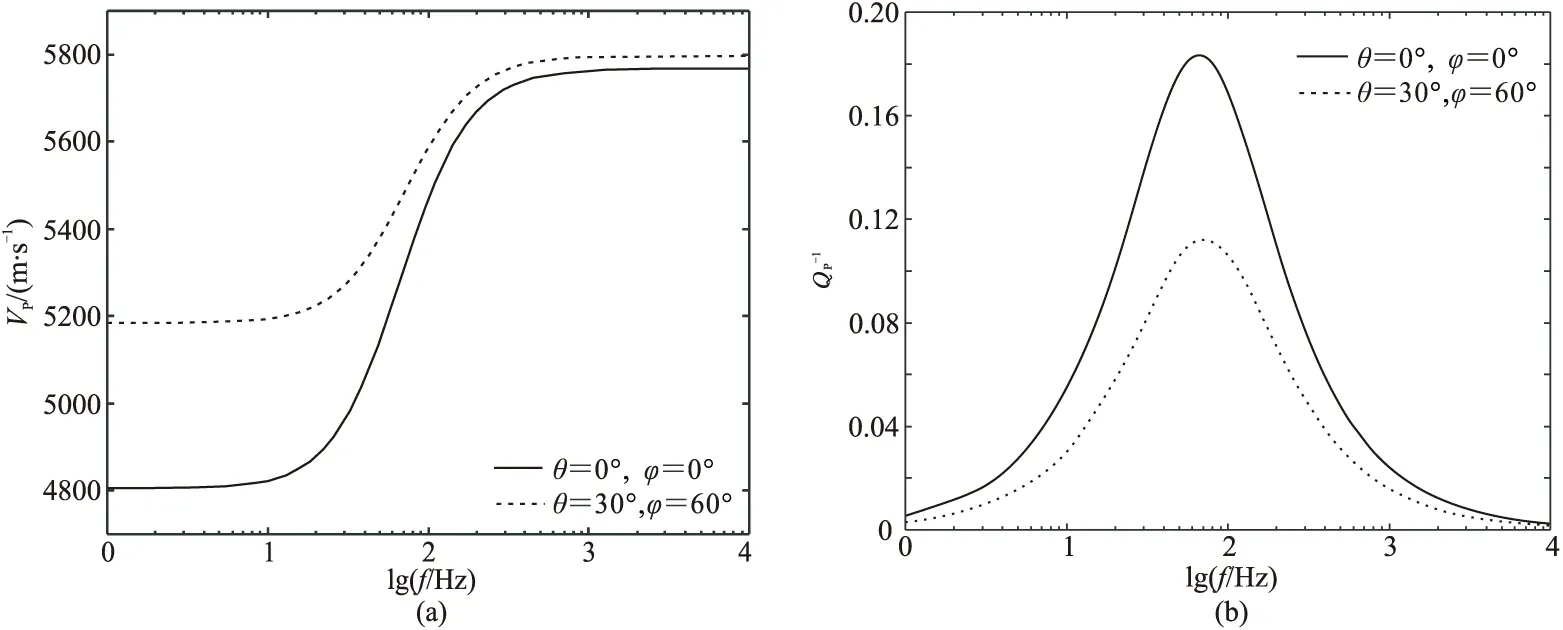
图1 不同裂缝方向的VP(a)和随频率f的变化曲线
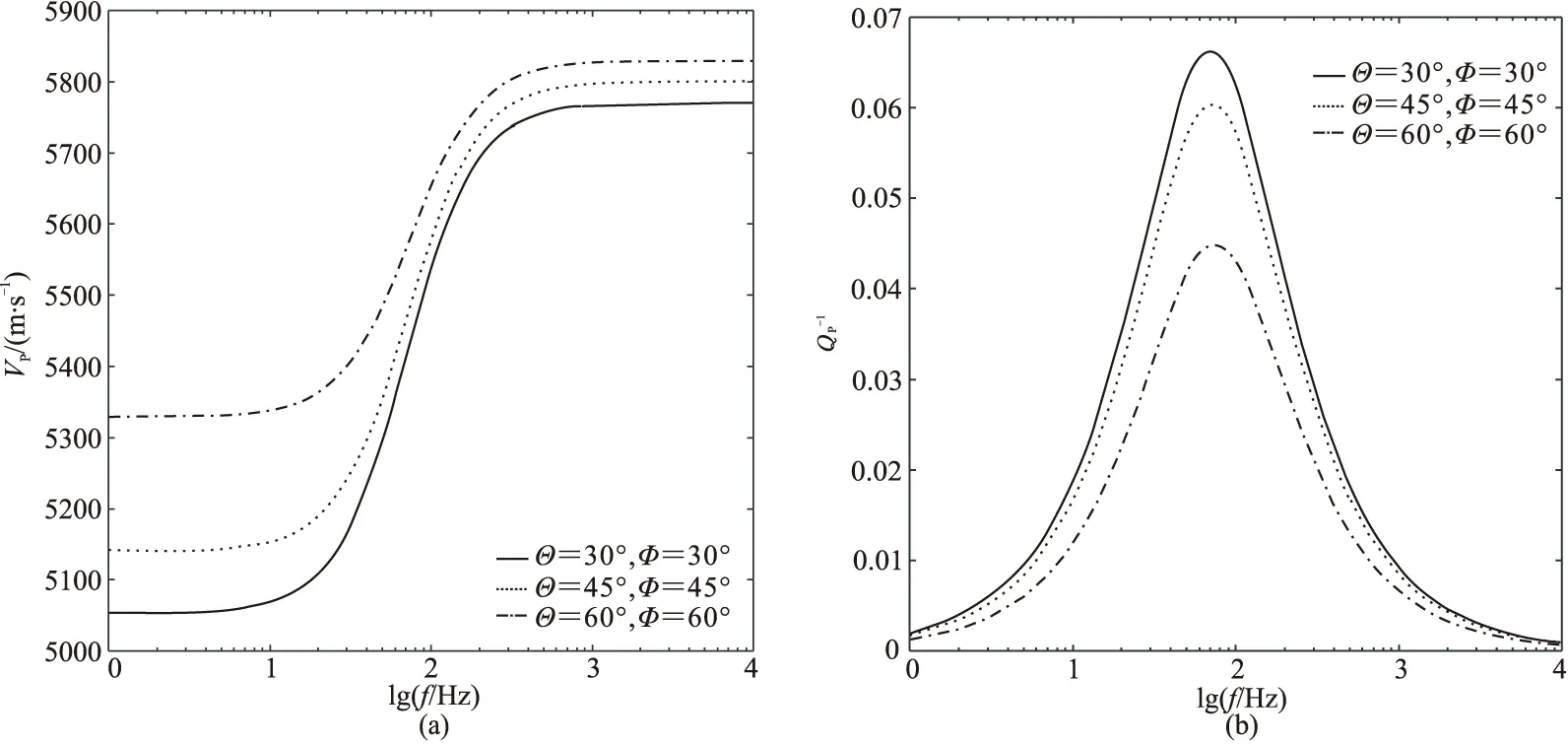
图2 不同入射方向的VP (a)和Q-1 P(b)随f的变化曲线地震波入射方向由入射角Θ和方位角Φ决定。模型中包含两组裂缝(θ=0°、φ=0°和θ=30°、φ=60°),
2.3 裂缝半径对地震波的作用
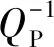
图3 不同r组合的VP (a)和Q-1 P (b)随f的变化曲线模型中包含两组水平排列的裂缝(θ=0°、φ=0°),法线方向为
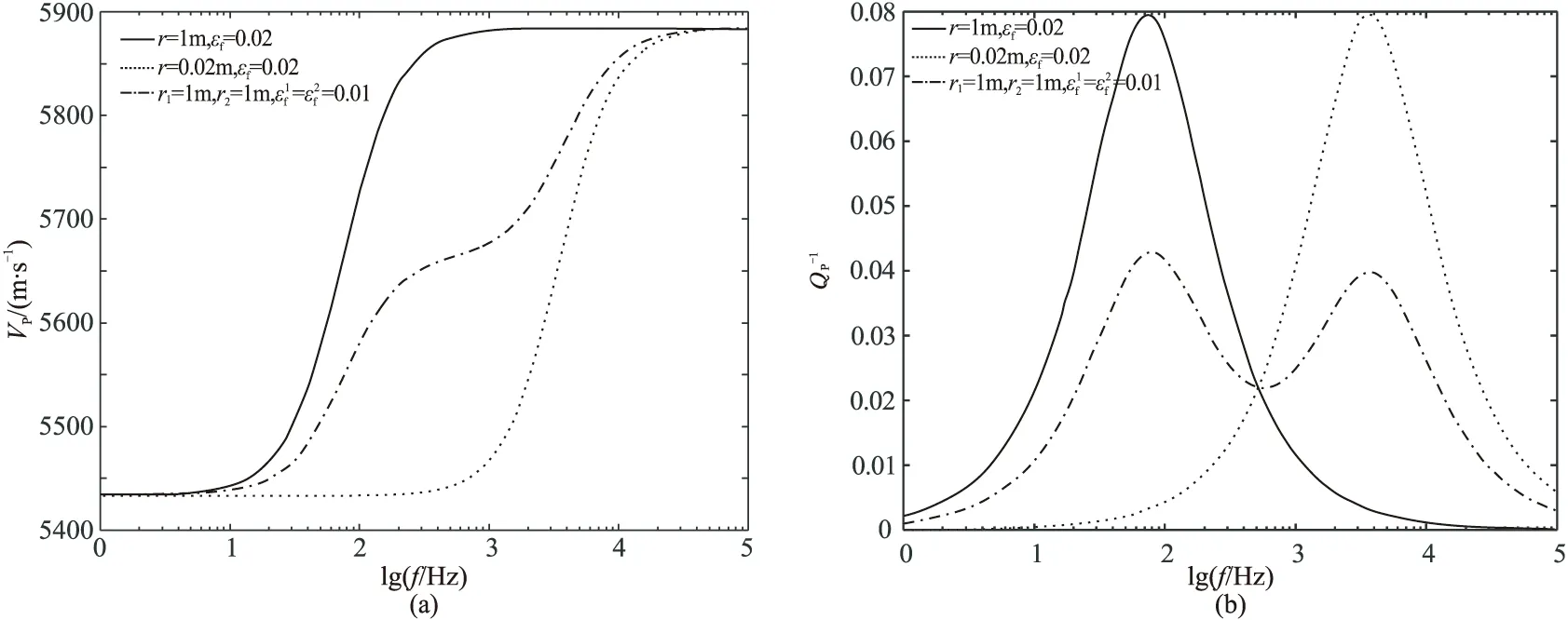
图4 不同裂缝发育情况的VP(a)和Q-1 P (b)随f的变化曲线
3 Chapman模型的黏弹性近似
黏弹性模型可以描述具有弛豫行为的黏弹性介质[23]。Picotti等[24]利用Cole-Cole模型研究了斑块饱和模型的地震波传播特性与频率变化规律,指出标准线性固体(SLS)模型适合模拟Biot理论模型和喷射流理论模型,而Cole-Cole模型可更好地近似斑块饱和模型。Chapman模型本质上是喷射流模型,因此可利用SLS模型对其模拟。弹性体和Kelvin-Voigt模型串联构成SLS模型,多个SLS模型并联构成广义标准线性固体(GSLS)模型。SLS模型的关键参数包括高频极限模量、低频极限模量和特征频率。通过上述数值模拟可知,裂缝半径控制特征频率,而裂缝方向、地震波入射方向和裂缝密度影响低频极限和高频极限模量(或最大逆品质因子),即控制频散和逆品质因子曲线形态。因此利用SLS模型近似Chapman模型的关键是寻找表征裂缝方向、地震波入射方向和裂缝密度共同作用的参数。
3.1 SLS模型模拟单裂缝模型
当模型中只有一组裂缝时,复模量M可由高频极限纵波模量M∞、低频极限纵波模量M0和特征圆频率ωc表示为
(3)
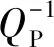
(4)
最大逆品质因子为
(5)
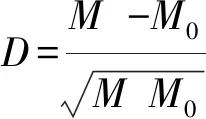
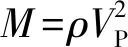
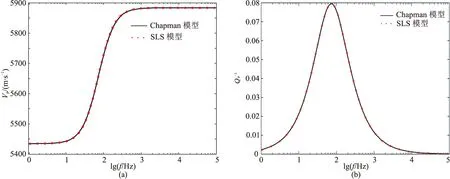
图5 SLS模型对Chapman单裂缝模型的模拟结果
3.2 GSLS模型模拟双裂缝模型
对于两组裂缝的情况,可以利用两组裂缝的模量损失代表两组裂缝的贡献。将式(3)拓展为包含两个特征频率的形式
(6)
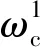
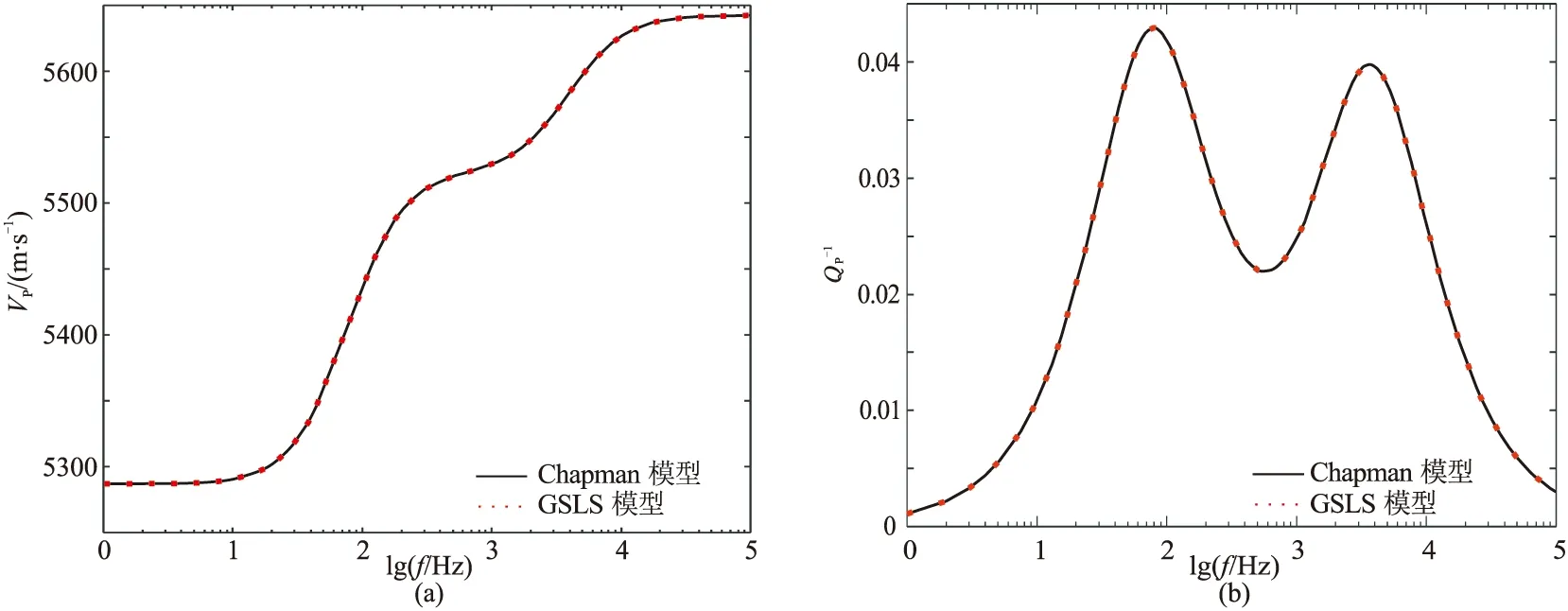
图6 GSLS模型对Chapman双裂缝模型的模拟结果
3.3 GSLS模型模拟多组裂缝模型
将式(6)拓展为包含n组裂缝的情况
(7)
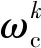
由于Chapman模型在低频时与Gassmann方程一致,在高频时与Hudson裂缝模型一致。因此,可以利用各向异性Gassmann方程计算M0,利用
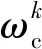
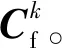
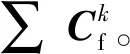
(8)
然后利用各向异性Gassmann方程将式(8)转换为饱和流体等效刚度矩阵Csat,其各分量为
(9)
其中
(10)
而
式中:Kg和Kl分别为基质和流体的体积模量;φs=φp+φf为总孔隙度,φp为孔隙孔隙度,φf为裂缝孔隙度。
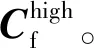
(11)
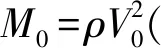
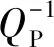
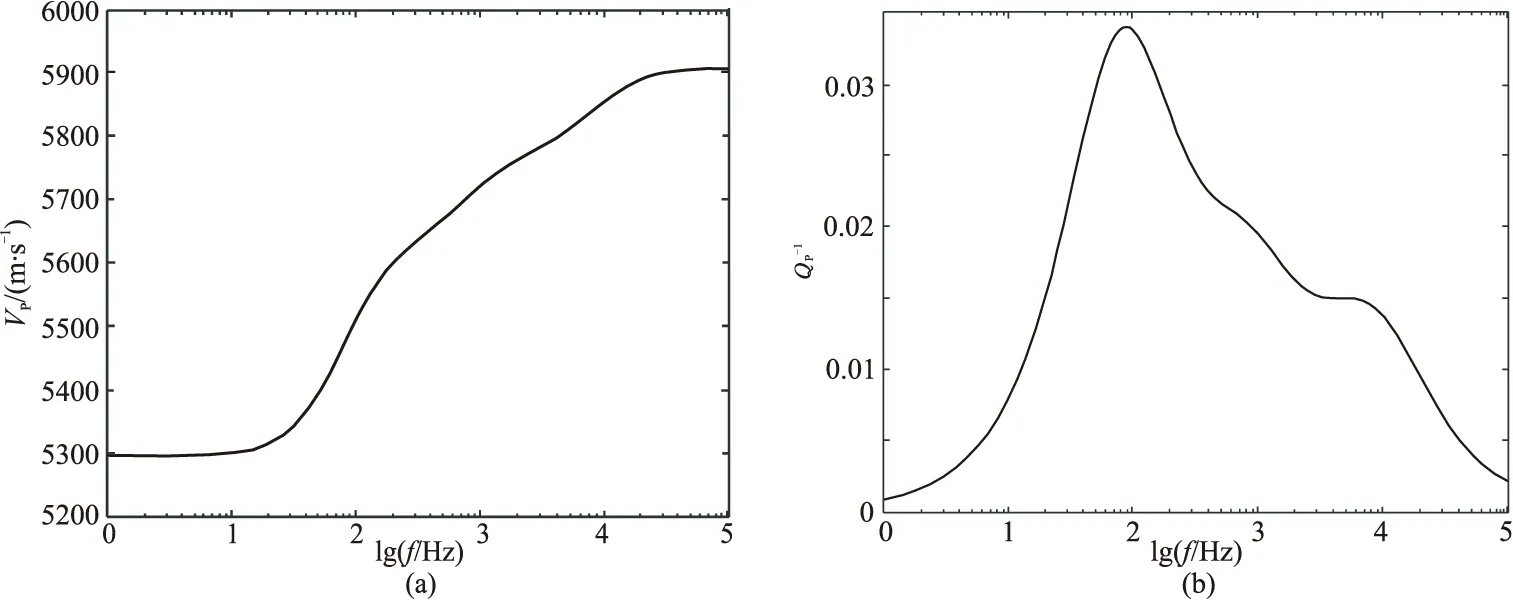
图7 正交各向异性介质模型的VP(a)和随f的变化曲线
4 讨论和结论
本文首先回顾了Chapman双裂缝模型的基本理论,分析了不同参数对纵波频散和衰减的影响,然后利用SLS模型模拟Chapman模型。通过GSLS模型可以计算包含多组裂缝的裂缝性孔隙介质中P波的频变特性。根据低频极限和高频极限情况下Chapman模型中孔隙校正项和裂缝校正项的解耦特征,提出了计算低频极限模量和高频极限模量的方法。在低频条件时,裂缝校正项与包含孔隙的背景项只有在干燥Chapman模型时才是解耦的。在高频条件时,裂缝校正项和包含孔隙的背景项无论在干燥还是饱和Chapman模型中都是解耦的,因此可利用Chapman模型和各向异性Gassmann方程得到低频模量,利用Chapman模型得到高频模量。
值得注意的是,当地震波传播方向与裂缝平行时,质点振动方向与裂缝方向平行,裂缝的挤压变形较小,特别是当裂缝中充斥着水、油等体积模量相对较大的流体时,裂缝的挤压变形较小。在这种情况下,裂缝表现出较强的刚度,裂缝的变形量较小。因此,P波速度随频率的变化很小,P波衰减达到最小。另外,本文没有考虑在裂缝互相连通的情况下流体在裂缝之间流动所产生的特征频率的现象。
虽然Chapman模型本身存在一些假设条件限制,如模型适应于孔隙度较低、裂缝形状最好为“硬币状”、孔隙空间中仅饱和单一流体等,影响了该模型的实际应用效果。但本文提出的基于Chapman模型和GSLS模型计算包含多组裂缝介质的P波频变特性的方法,对于研究各向异性介质的地震波场特征及地震响应机理具有一定实际意义。

