破碎围岩隧道二次衬砌施作时机研究

胡 丰 产，刘 忠，李 奇，吴 松 锋

(1.河南省核技术应用中心，河南 郑州 450044； 2.黄河水利委员会 黄河水利科学研究院，河南 郑州 450003)

0 引 言

随着中国交通建设的迅速发展，公路、铁路网已逐步向复杂地质区域延伸[1-2]。隧道作为道路穿山的主要手段，很多情况下不得不穿越软弱、破碎围岩带。新奥法作为在软弱、破碎围岩区修建隧道最为有效的方法，其理论认为，在进行隧道支护时应使围岩与支护结构共同承担围岩压力，即充分发挥围岩的自承能力[3]。因此，在实际隧道施工过程中，往往会根据地质条件为初支结构预留一定的变形量，待围岩应力释放至一定程度时再施作二次衬砌，二次衬砌理论上会承担一部分围岩压力，由于其强度有限，这种情况下二次衬砌的施作时机便显得尤为重要。若施作时机过早，围岩应力释放不充分，二次衬砌由于承担过大的围岩压力而易开裂、掉块；若施作时机过晚，易导致初支结构变形过大，严重威胁施工安全[4]。基于此，学者们对隧道二次衬砌的施作时机进行了广泛的研究。

孙均等[5]最早在自己的《地下结构》一书中对围岩的剪切应变进行了分析，认为当围岩的剪应变达到相应岩性下的剪应变允许值时即可施作二次衬砌。此后，中国出版的几部隧道规范[6-8]都对二次衬砌的施作时机进行了要求，但并未针对具体地质情况给出定量标准。刘志春等[9]以乌鞘岭隧道为依托，通过现场监测变形量和变形速率与弹性位移解之间的关系确定了二次衬砌的施作时机。陈军[10]、刘国庆[11]、齐龙飞[12]等以与掌子面的距离为标准，采用有限元软件研究了隧道二次衬砌的施作时机。王睿等[13]采用概率统计法分析了数十个隧道断面的变形监测数据，推导出了围岩基本稳定的时间，并以此作为二次衬砌合理施作时机的依据。杨峰[14]基于监控量测数据建立了一种变形动态综合评估模型，通过模型计算了围岩的稳定时间并将其作为二次衬砌施作的时机。王士民等[15]采用相似模拟试验确定了盾构隧道的双层衬砌合理施作时机为结构变形达到57%～83%时。郭小龙等[16]对现场监测数据进行了回归分析，以隧道变形稳定时间为变量推导出了二次衬砌施作时机的概率密度函数。

在未来的十几年中，中国还将在中西部地区修建大量的穿山隧道[17]，隧道施工会面临越来越多的破碎围岩带。与常规围岩不同的是，破碎围岩的岩体完整性差、围岩变形量大且容易失稳[18]，围岩自稳时间因破碎程度的不同而差异巨大，导致二次衬砌施作时机难以确定，由于衬砌施作时机不当导致的衬砌破坏事故时有发生[19-21]，而目前针对隧道二次衬砌施作时机的研究鲜有考虑破碎岩体的问题，难以指导破碎围岩隧道衬砌施工。本文以雅康高速紫石隧道为依托，将Hoek-Brown强度准则写入Abaqus有限元软件中，通过准则中的GSI参数描述岩体破碎程度，并采用追踪单元法消除了支护结构与破碎岩体间的节点接触和耦合问题，计算了不同围岩位移释放率下的初期支护和二次衬砌应力，基于安全系数确定了二次衬砌的最佳施作时机。

1 工程概况

雅康高速东起四川省雅安市草坝镇，西至甘孜藏族自治州康定市，公路全长134 km，由于路址区内拥有二郎山、贡嘎山等多座极高山岭，公路全线共设隧道29座。紫石隧道为雅康高速控制性工程之一，位于雅安市天泉县境内，隧道采用分离式设计，左线桩号ZK52+538～ZK54+500，右线桩号K52+540～K54+500，隧道全长4.8 km，属特长隧道。隧道断面采用三心圆设计，上半圆半径0.553 m，拱高0.715 m，净空面积78.23 m2。隧址区内岩质以白云岩、灰岩、薄层泥岩、砂岩等为主，其中白云岩岩体极其破碎，多呈颗粒状，为典型的破碎围岩带，围岩等级IV～V级。

隧道采用三台阶预留核心土七步开挖法进行施工，围岩质量较好区域改为两台阶施工，各级围岩支护参数见表1。

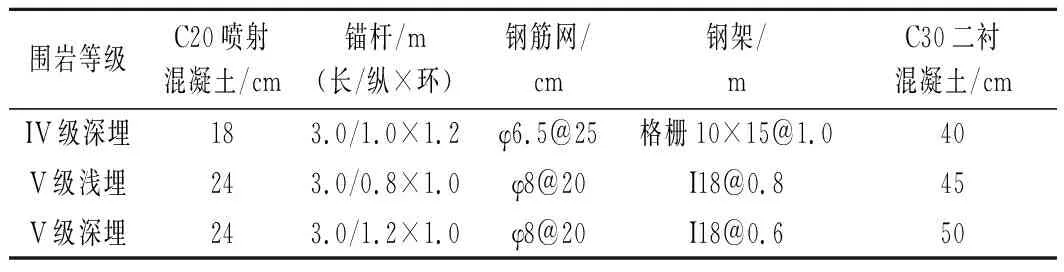
表1 雅康高速紫石隧道支护参数Tab.1 Support parameters of Zishi tunnel in Yakang Expressway

2 数值模型建立

为探究紫石隧道二次衬砌最优施作时机，采用Abaqus有限元软件对隧道实际施工情况进行模拟，根据隧道围岩的最终变形结果，分别设置位移释放率为85%，90%，95%和100%，分析不同工况下的锚杆、钢拱架、喷射混凝土以及二次衬砌应力大小。

2.1 考虑岩体破碎程度的强度理论二次开发

该隧道围岩岩体破碎，岩体变形表现为显著的非线性，当进行数值计算时，若仍采用传统的Mohr-Coulomb强度理论作为屈服准则，将忽略破碎岩体的非线性特征，致使计算结果与实际情况相差较大，难以为破碎围岩隧道施工提供有效参考。1980年，Hoek和Brown在进行地下硐室开挖的研究过程中，总结了大量岩石试验数据，推导出一种用于岩石破坏预测的经验公式，即Hoek-Brown强度理论[22]：

(1)

式中：σ1和σ3分别为最大和最小主应力；σc为岩石单轴抗压强度；mi为与岩石硬度相关的系数。在此后的应用过程中，Hoek和Brown对该公式进行了不断的改进，最终形成了广义Hoek-Brown强度理论：

(2)

式中：mb、s、α为与岩体自身性质有关的参数，可采用下式确定3个参数的大小：

(3)

式中：GSI为地质强度指标；D为爆破扰动因子。由于GSI值与岩体破碎程度相关，因此Hoek-Brown强度理论可以较好地适用于破碎岩体的变形破坏计算当中。

为了使Hoek-Brown强度理论可以在Abaqus有限元软件中得到应用，使用UMAT子程序对Abaqus进行二次开发，具体操作流程如图1所示。

2.2 衬砌单元前处理

在传统的数值计算过程中，建立模型单元的方法是在该单元的原始位置予以激活，这就导致当人为确定位移释放率后，新激活的模型单元会在节点接触和耦合位置产生初始应变，致使计算结果过于保守，无法与实际情况相吻合。本文采用“追踪单元法”进行衬砌施作过程的模拟，如图2所示，具体流程如下。

(1) 在相同几何位置设追踪单元和衬砌位置岩体，追踪单元(衬砌)与衬砌位置岩体的单元形状完全一致且共享节点(节点编号一致，但具有不同单元号)。

(2) 在模型地应力平衡前将追踪单元“剔除”，由于追踪单元与衬砌位置岩体共享节点，且该单元的刚度和自重“无限小”，因此当岩体变形时追踪单元可以追踪衬砌位置岩体的相应位置。

(3) 激活“追踪单元”，激活后的追踪单元具有衬砌的材料属性，追踪单元激活后转换为衬砌。

2.3 模型建立

采用Abaqus有限元软件进行数值模拟计算，分别建立紫石隧道IV级围岩深埋段、V级围岩深埋段以及V级围岩浅埋段模型，计算所选断面信息如表2所列。依据圣维南原理，为消除尺寸效应，模型水平方向左右各取6倍洞径，上部取实际埋深，下部取5倍洞径，模型计算参数见表3，数值模型见图3。依据紫石隧道的现场地质勘探结果、施工爆破情况以及现场岩样的室内试验结果，取Hoek-Brown强度准则参数如表4所列。

表2 计算断面信息Tab.2 Calculation section information

表3 模型计算参数Tab.3 Model calculation parameters

表4 Hoek-Brown参数取值Tab.4 Hoek-Brown parameters

3 数值模拟结果分析

为获得不同围岩等级段隧道二次衬砌施作最优时机，分别对各级围岩段的初期支护应力以及二次衬砌内力进行了计算，按图4提取关键点位置的计算结果。

3.1 初期支护应力计算结果分析

初期支护结构应力计算结果如表5所列，由于篇幅限制，仅展示最大应力点出现位置的应力结果。根据表5的计算结果，绘制不同位移释放率下钢架应力、锚杆应力以及喷射混凝土应力曲线如图5所示。由图5可知：当位移释放率一定时，IV级围岩的初期支护(钢架、锚杆和喷射混凝土)应力明显小于V级围岩，V级围岩深埋段与浅埋段的初期支护应力相差不大，各位移释放率以及不同围岩等级下的钢架最大应力点和喷射混凝土应力点均出现在拱顶处，锚杆最大应力点均出现在右边墙处。

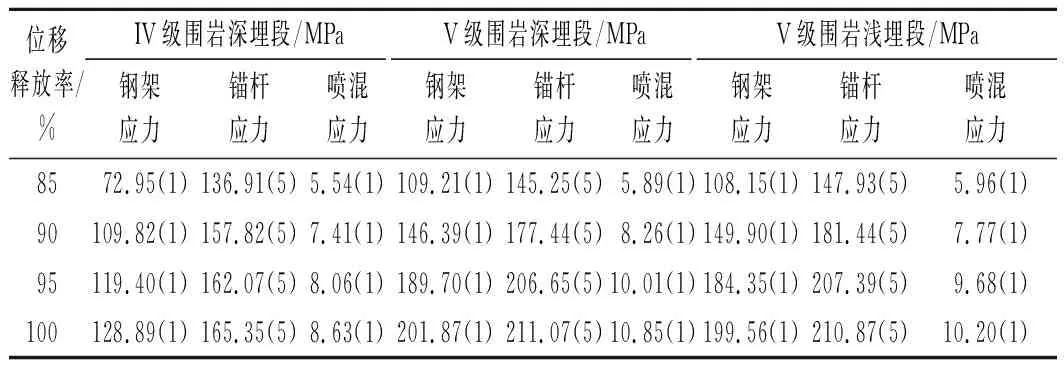
表5 初期支护计算结果Tab.5 Calculation results of primary support

当围岩等级一定时，随着位移释放率的增加，初期支护应力均增加。对于IV级围岩深埋段来说，当位移释放率未达到90%时，初支结构应力增长较快；当位移释放率达到90%后，初支结构的应力增幅明显放缓；当位移释放率从90%提升至100%时，钢架、锚杆和喷射混凝土的应力增幅仅为17.3%，4.8%和16.5%。对于V级围岩深埋段和浅埋段来说，当位移释放率达到95%后，初支结构应力的增幅开始明显放缓；当位移释放率从95%提升至100%时，V级围岩深埋段和浅埋段的钢架、锚杆和喷射混凝土应力增幅均在10%以内。

综上所述，当IV级围岩深埋段的位移释放率达到90%、V级围岩段的位移释放率达到95%时，支护结构已充分发挥承载能力，且围岩自承能力也被最大限度的发挥。随着位移释放率的增大，钢架与锚杆的应力值与增幅值都明显大于喷射混凝土，证明在锚喷支护中，钢架与锚杆起主要支撑作用。钢架、锚杆和喷射混凝土的最大应力均出现在V级围岩深埋段，分别为201.87，211.07 MPa和10.85 MPa，所有应力均在规范允许值以内，证明初支结构安全可靠。

3.2 二次衬砌内力结果分析

二次衬砌轴力、弯矩和应力计算结果见表6。由表6可知：二次衬砌的应力值、轴力值和弯矩值整体上随着位移释放率的增大而减小，随着围岩等级的增大而增大，V级围岩深埋段和浅埋段的二衬内力相差不大。各级围岩的最大拉应力出现在拱顶处，最大压应力出现在右拱脚处，最大轴力出现在拱顶处，最大弯矩出现在右拱脚处。IV级围岩深埋段的最大拉应力和最大压应力分别为1.37 MPa和1.30 MPa，V级围岩深埋段的最大拉应力和最大压应力分别为1.49 MPa和1.64 MPa，V级围岩浅埋段的最大拉应力和最大压应力分别为1.42 MPa和1.56 MPa，二次衬砌的应力值均小于C30混凝土的抗拉和抗压强度设计值。IV级围岩深埋段的最大轴力和最大弯矩分别为190.17 kN和7.75 kN·m，V级围岩深埋段的最大轴力和最大弯矩分别为220.61 kN和7.95 kN·m，V级围岩浅埋段的最大轴力和最大弯矩分别为209.58 kN和7.55 kN·m，各围岩段二次衬砌内力均较小。

表6 二次衬砌计算结果Tab.6 Calculation results of secondary lining

4 二次衬砌安全性对比

为分析二次衬砌在使用过程中的安全性能，根据JTG 3370.1-2018《公路隧道设计规范 第一册 土建工程》[23]的相关要求，当混凝土承受永久荷载与基本可变荷载时，为保证混凝土结构不受到破坏，其安全系数K必须满足K≥2.4。对混凝土偏心受压构件的安全系数进行计算，计算结果如表7所列。由表7可知：对于IV级围岩深埋段，当位移释放率小于90%时，拱顶的安全系数仅为2.15，二次衬砌具有开裂风险；当位移释放率在90%以上时，二次衬砌混凝土安全系数均大于2.4，二次衬砌结构安全可靠。结合初期支护内力的分析结果，可将位移释放率达到90%作为二次衬砌施作时机。对于V级围岩深埋段和V级围岩浅埋段，当位移释放率小于95%时，拱顶的安全系数低于2.4，二次衬砌具有开裂风险；当位移释放率在95%以上时，二次衬砌混凝土安全系数均大于2.4，二次衬砌结构安全可靠，此时可将位移释放率达到95%作为二次衬砌施作时机。

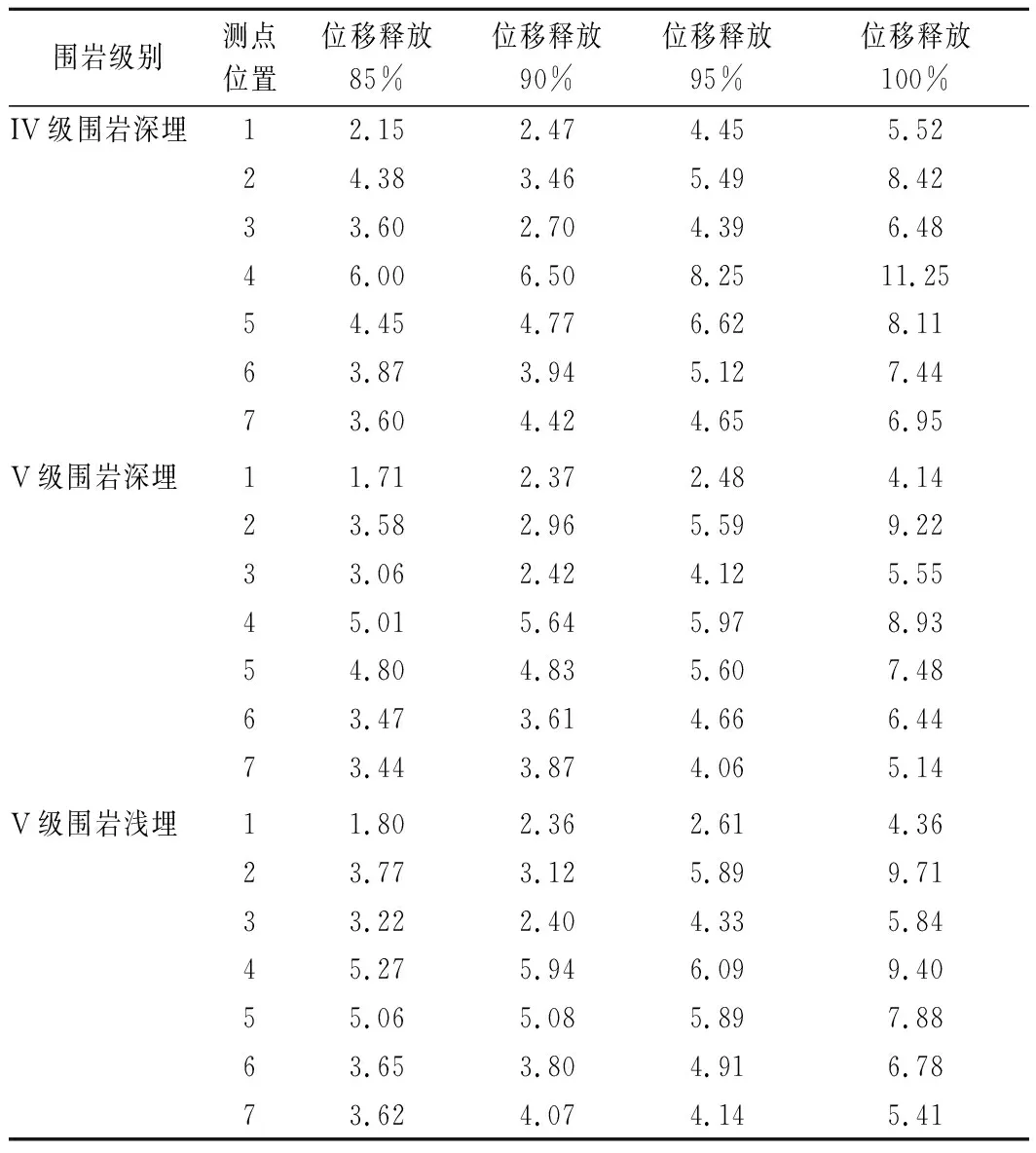
表7 安全系数计算结果Tab.7 Calculation results of safety factor

5 结 论

以雅康高速紫石隧道为研究对象，采用Abaqus数值模拟软件建立了多种围岩级别下的初期支护结构及二次衬砌结构计算模型，通过数值模拟计算及安全系数对比确定了二次衬砌的最优施作时机，获得以下结论。

(1) 从初期支护应力计算结果可见，IV级围岩深埋段和V级围岩段的初期支护应力在围岩位移释放率分别达到90%和95%以后增长趋于平缓，证明此时的应力释放已基本完成，支护结构已充分发挥承载能力。钢架、锚杆和喷射混凝土的最大应力分别为201.87，211.07 MPa和10.85 MPa，均在规范允许值以内，证明初支结构安全可靠。

(2) 从二次衬砌内力计算结果可见，二次衬砌的拉应力和压应力均小于C30混凝土的抗拉和抗压强度设计值，二次衬砌的轴力和弯矩均较小。

(3) 二次衬砌安全系数计算结果表明：当位移释放率达到90%时施作IV级围岩深埋段的二次衬砌，95%时施作V级围岩深埋段和浅埋段的二次衬砌时，不具备开裂风险，二衬结构安全可靠。

(4) 在实际隧道施工中，结合施工现场的变形监测结果，可将位移释放率达到90%时作为紫石隧道IV级围岩深埋段二次衬砌的施作时机，95%时作为V级围岩段二次衬砌的施作时机。

由于二次衬砌无需在围岩位移释放率达到100%时进行施作，因此可最大程度节省隧道施工工期，对保证破碎围岩隧道施工安全、提高隧道施工效率具有重要意义，研究成果可为类似工程提供参考与借鉴。

隧道在开挖过程中，围岩的应力释放和变形具有一定的时间效应。本文在计算时所采用的Hoek-Brown强度准则并不能考虑时间因素，使得二衬施作时机必须依据变形监测结果进行确定。在今后的研究中可对强度准则进行改进，将时间作为变量考虑到计算过程内，为二衬施作时机提供时间维度的参考。