基于NSCT和分数阶微分的多聚焦图像融合方法

朱亚辉

(陕西学前师范学院 数学与统计学院,陕西 西安 710100)

由于受外部环境的影响及相机本身固有的不足，往往难以得到某个场景的全聚焦图像。利用多聚焦图像融合技术，获得全图聚焦清晰、细节丰富的图像。这在机器视觉、遥感监测等方面具有非常重要的应用，越来越多的学者提出了许多的多聚焦图像融合方法。如张亚峰等人将线性延迟相位滤波器推广到非线性群延迟相位滤波器，设计出基于扩展相位拉伸变换局部相位方差独立的融合策略，该方法优于传统融合算法，但也存在图像边缘能力描述不佳的问题；欧阳宁等提出了基于自适应稀疏表示的多聚焦图像融合，虽然该方法客观融合效果评价指标值较好，但由于字典矩阵在描述图像边缘等方面能力不佳，部分细节信息被平滑处理。屈小波等提出非降采样轮廓波(Non-sampling-down Contourlet, NSCT)域内空间频率激励的图像融合算法，该方法在描述显著目标的边缘上能力不佳。分数阶微分算子具有弱导性，既能很好地提取图像的边缘信息，又能较好地保留平滑区域的弱边缘信息。因此，分数阶微分算子在图像去噪、图像增强和图像边缘检测等方面取得较好的应用。

鉴于上述分析，在现有研究的基础上，提出了一种基于NSCT和分数阶微分的多聚焦图像融合方法。首先经NSCT将多聚焦图像分解一个低频子带和多个高频子带；其次，根据各子带的特征，设置不同的融合规则。其中，低频子带采用源图像与低频图像间的局部对比度差的绝对值最大为融合规则；高频子带采用基于分数阶微分梯度最大为融合规则。实验结果表明，本融合方法在主、客观评价中都有较好的性能。

1 基本理论

1.1 图像NSCT分解

NSCT是由非下采样方向滤波器(Non-sampling-down directional filter, NSDFB)和非下采样金字塔(Non-sampling-down pyramid, NSP)两部分而组成。图1为NSCT变换三级分解结构图。

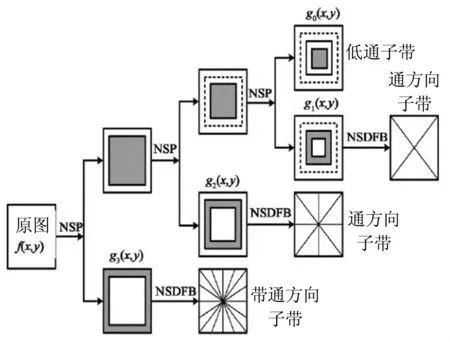
图1 NSCT变换三级分解结构图

1.2 分数阶微分滤波器

分数阶微分是一种常用的图像增强算法，该算法相比于整数阶微分算法可以更好地检测模糊边界和微弱细节，调整图像的对比度图像细节更突出而且还保留了平滑区域的纹理信息，改视觉质。

目前，Grümwald-Letnikov分数阶微分常常用于数字图像处理中，其数学表达式为：

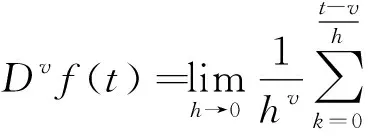
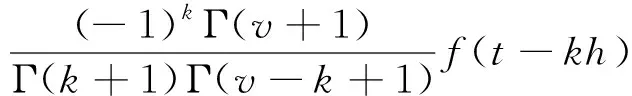
其中：表示此式为分数阶微积分呢，()表示积分时间步长；()为伽马函数。

若()的持续期∈[,]，将函数持续期间[,]按单位间隔=1进行等分，得到：

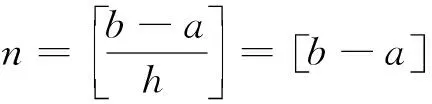
则一元函数()的阶分数阶微分差分表达式为：

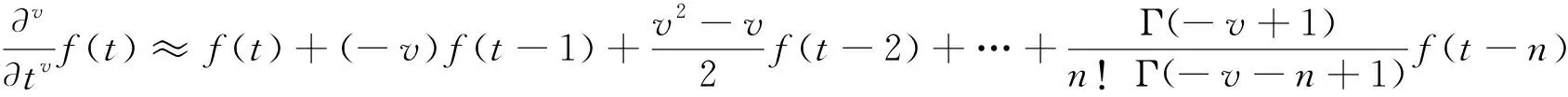
(1)

应用公式(1)前3项，求取5×5八方向的分数阶微分掩模算子，图2为叠加后得到的掩模。

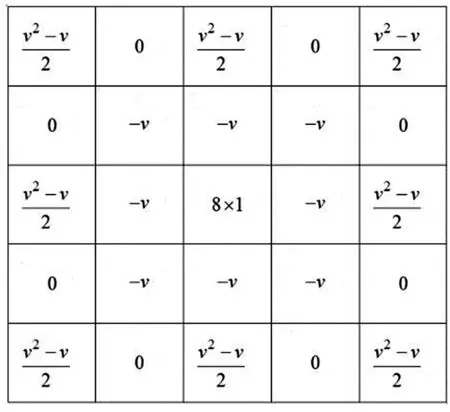
图2 5×5掩模

文献[10]和文献[11]证明，基于分数阶微分的边缘检测，既能很好地提取图像边缘信息，又能较好地保留平滑区域的弱边缘信息。

2 融合方法及融合规则

已知两幅多聚焦图像,，首先采用NSCT将图像,分解为低频子带,和高频子带{},{}；再分别采用局部对比度差的绝对值最大和基于分数阶微分的梯度最大为融合规则，最后采用逆NSCT得到融合图像。

2.1 低频子带融合规则

一般情况下，图像经过NSCT变换分解得到的低频分量集中反映图像基本信息。图3为左右聚焦源图像及其低频子带。

由图3可知：当区域为聚焦区域时，该区域与其相应低频区域的局部对比度变化强烈；当区域为模糊区域时，该区域与其相应低频区域的局部对比度变化缓慢。因此，将源图像与其低频子带间的局部对比度差的绝对值最大作为决策图。

图3 源图像及其低频子带

具体融合规则公式为：

其中，=|()-()|,=|()-()|.

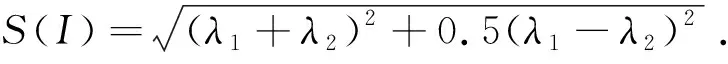
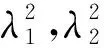
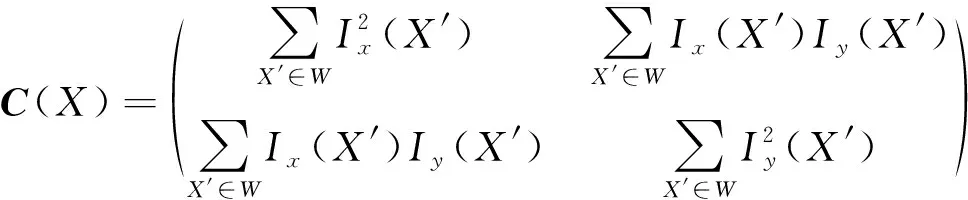
(′)和(′)分别沿着,方向的梯度。

图4为低频子带决策图。

图4 低频子带的决策图

由图4可以看出，通过计算源图像与低频子带的局部对比度绝对值差可以获得较好的决策图。

2.2 高频子带融合规则

高频子带描述源图像的边缘信息。分数阶微分相比于整数阶微分算法能更好地检测模糊边界和微弱细节，调整图像的对比度图像细节更突出，而且保留了平滑区域的纹理信息。因此，高频融合规则采用边缘梯度最大原则，其中边缘检测算法采用分数阶微分算法。高频融合规则如下：

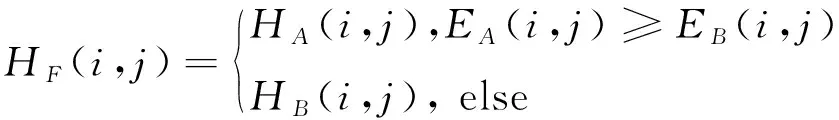
其中，为基于分数阶微分算法的梯度，表达式如下：=max{,,,,,,,},其中，8个方向的掩模如图2所示。

3 实验及结果分析

3.1 实验参数的设计及融合图像的生成

在本节中，通过主、客观评价多组融合图像的效果，分析本文融合方法的有效性。其中，4组多聚焦源图像对分别为：“Clock”“Pepsi”“Desk”和“Flower”；采用的融合方法包括：文献[4]融合方法、文献[13]融合方法、文献[14]融合方法和本文方法。其中，本文融合方法的参数设置如下：分解级数为4级，滤波器参数为'pyrexc' 和'vk'，分解方向数为[2 3 3 4]，分数阶数=09。多种方法的融合结果如图5所示，其中图5(a)和图5(b)为多聚焦源图像对，图5(c)～图5(f)分别为文献[4]、文献[13]、文献[14]和本文方法。

图5 多聚焦图像对及融合结果示意图

3.2 融合图像的主观评价

对比第1组融合结果可以看出，基于文献[4]的融合图像右边闹钟表盘纹理边缘不清晰；基于文献[13]的融合图像左边小闹钟的边缘较为模糊；基于文献[14]的融合方法和本文融合方法融合效果均较好。

对比第2组的融合结果可以看出，基于文献[13]的融合图像纹理较为模糊，字母出现重影；基于文献[14]的融合图像右下角边缘不清；基于文献[4]的融合图像右端文字较为模糊。基于本文方法的融合图像纹理清晰，尤其字体清晰，无重影。

本文融合方法的优势同样体现在第3组和第4组的融合图像中。例如，在第3组中，本文方法较好地保留等纹理信息；在第4组中，在本文方法的融合结果中，“花”在结果图像中对比度适中，背景细节信息清晰；总体来说，在视觉质量上，本文融合方法较优于其他图像融合方法。

3.3 融合图像的客观评价

为了更加客观地评价本文融合方法的有效性，应用边缘信息保留度(Edge Information Retention, EIR), 特征相似度(Feature Similarity, FS), 结构相似度(Structural Similarity, SSIM)和特性互信息(Feature Mutual Information, FMI)评价融合图像质量，这4个指标数值越大，则融合效果越好。表1～表4给出了多组融合图像的客观评价指标值。

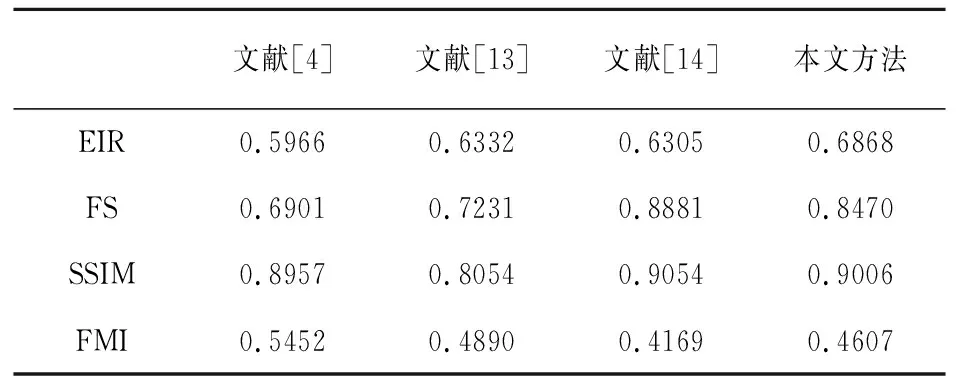
表1 Clock融合结果评价

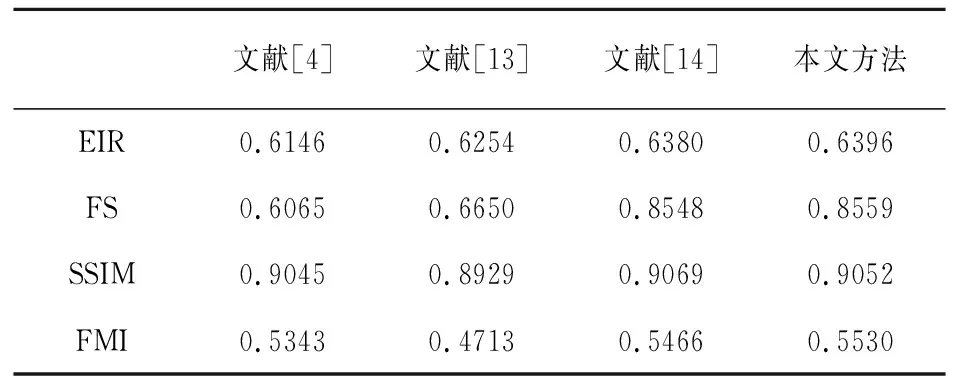
表2 Pepsi融合结果评价

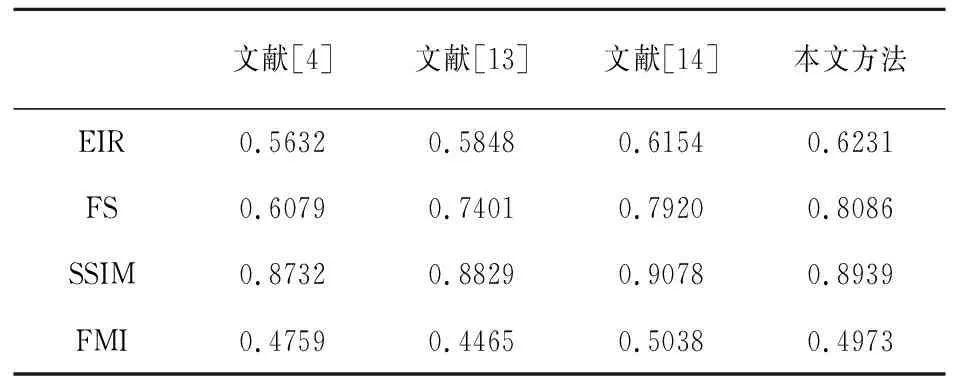
表3 Desk融合结果评价

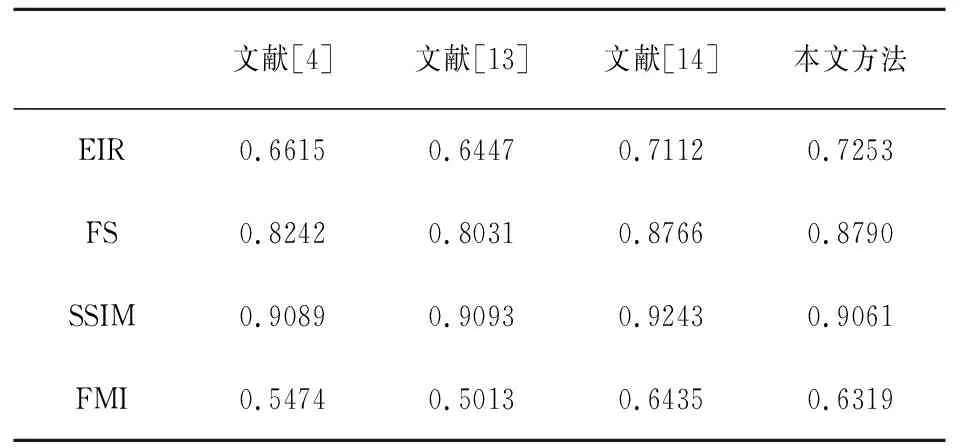
表4 Flower融合结果评价

由表1～表4可知，对于“EIR”,本文融合方法均优于其他融合方法，表明本文融合方法很好地保留更多的边缘信息；对于“FS”，本文融合方法在“Pepsi”“Desk”和“Flower”图像融合结果评价值最优，但在“Clock”融合图像上本文融合方法次之(表1)，表明了本文融合方法较好地保留了源图像的特征；对于“SSIM”和“FMI”这两个评价指标，虽然本文融合方法根据优劣排序并不是最优的，但与最优值相差不多，表明本文融合方法较好地保留了结构相似性和特征互信息性。总之，从整体上，本文融合方法具有较好的融合结果。

4 结 论

NSCT能增强图像的平移不变性，但在描述显著目标的边缘上能力不佳。分数阶微分算子既能很好地提取图像的边缘信息，还能较好地保留平滑区域的弱边缘信息。为了弥补NSCT的不足，提出了基于NSCT和分数阶微分的多聚焦图像融合方法。通过对比多组融合图像主、客观评价结果表明，该方法能有效保留边缘信息。