基于改进强化学习的模块化自重构机器人编队

李伟科，岳洪伟，王宏民，杨 勇，赵 敏，邓辅秦,,†

(1. 五邑大学 智能制造学部, 广东 江门 529020；2. 深圳市人工智能与机器人研究院, 广东 深圳 518116；3. 深圳市杉川机器人有限公司, 广东 深圳 518006；4．中电科普天科技股份有限公司研发中心，广东 广州 510310)

随着计算机技术、控制理论和人工智能理论的不断发展与成熟，模块化自重构机器人(MSRR)系统的研究近年来已经成为一个热点。MSRR系统有多个相同的物理模块，可以自由地相对移动，相互连接或者断开。这些模块通过改变它们的相对位置和连接，重新排列成不同形态的机器人。MSRR通过避开不同的环境障碍物，以满足不同的任务要求。因此，MSRR系统在通用性、鲁棒性和低成本方面要优于传统的固定形态的机器人。这种系统特别适用于工作环境大、操作任务复杂的场合，如紧急搜索、救援、核电站维修等领域。在这些场景中，MSRR必须在短时间内到达目标点，形成任务所需的队形。因此，文中讨论的问题是MSRR如何避开障碍物，在短时间内到达指定的目标点(即路径规划)，以形成指定的队形。基于不同的任务需求，MSRR可以进一步形成任务所需的形态解决复杂未知的任务。MSRR在形成指定的队形前，需要规划前往指定目标点的最优路径。文献[12]提出了一种基于网格的滑动立方体自重构机器人，并提出了一种基于Cellular Automata的自重构算法来控制机器人避开障碍物。文献[13]受强化学习算法的启发，提出一种用于滑动立方体的Million Module March的算法。然而，由于这些算法是在具有滑动立方体形状的模块化机器人中实现的，它们受到滑动立方体物理形状的限制，只能避开立方体模块大小的障碍物。

文献[3]将MSRR从一种形态转换为最终形态的动作序列定义为自重构(SR)过程。在自重构问题(SRP)中，研究者使用马尔科夫决策过程(MDP)来规划两个模块单元之间的路径，使偏离目标位置的模块单元能够移动到其目标点。然而，基于MDP算法规划的路径很容易相交，导致机器人之间发生碰撞、锁死和失去连接。

在强化学习中，智能体是通过与环境的不断交互和奖励信号的反馈学习策略的。文献[13]受到强化学习的启发，提出一种Million Module March的算法，使智能体避开障碍物，并形成指定队形。文献[17]将SRP建模为强化学习问题，成功地将Q-learning算法应用在智能体中，并让智能体学习如何自主在相邻模块之间形成指定的直线(Line)、连接模块网格(Mass)和模块形成的环路 (Ring)三种形状。由于传统的Q-learning算法在训练的初始阶段缺乏对周围环境的先验知识，智能体会随机选择动作，造成迭代次数的浪费和算法收敛速度的缓慢。为了缓解这些问题，文献[19]提出基于知识共享的Q-learning策略来实现不同智能体之间的信息交互。文献[20]进一步提出了一种基于环境知识共享的群体Q-learning算法(SQL-SIE)来加速算法的收敛。然而，上述算法在MSRR进行队形转换时需要进行二次训练，以形成不同的队形形状。此外，上述算法在训练智能体从起始点前往目标点时，并没有合适的奖励引导智能体向有利于前往目标点的方向移动，这会导致算法的迭代次数增大，算法难以收敛。为了解决以上问题，文中提出一个两阶段的强化学习算法来解决MSRR的编队控制问题。在第一阶段，利用基于群体和知识共享的Q-learning训练所有机器人前往二维离散地图的中心点，以获得一个包含全局地图信息的最优共享Q表。在这个阶段中，文中引入曼哈顿距离作为奖赏值，引导智能体更快向目标点的方向移动，以减小迭代次数，加快算法的收敛速度。在第二阶段，机器人根据第一阶段获得的最优共享Q表和当前所处的位置，找到前往指定目标点的最优路径。

文中算法的贡献如下：

(1)该算法在第一阶段是训练四周的机器人前往地图的中心点，所以获得的最优共享Q表包含的地图信息比较全面，智能体可以根据这个最优共享Q表和当前所处的位置，找到前往地图任意一点最优路径。

(2)该算法在MSRR进行多次队形转换时，不需要多次训练，节省大量的运行时间，算法的收敛速度快。

(3)该算法引入了曼哈顿距离作为奖赏值，引导智能体向有利于目标点的方向移动，以减小迭代次数，加快算法的收敛速度。

1 多智能体编队的问题描述

文中考虑的MSRR系统如图1所示，这是一种小型的球形机器人，内部有两个在塑料防水壳内表面上滚动的电机，使机器人可以移动。

图1 MSRR系统

文中在数学上将MSRR建模成智能体，因此将MSRR的编队控制问题看作是多智能体编队控制问题。这种问题主要分为两种：第一种是每个智能体移动到各自指定的目标点以形成指定的队形。第二种是每个智能体保持初始队形向目标点移动。文中要解决的是第一种编队控制问题。智能体需要到达指定的目标点，不能占据其他智能体的目标点。如果智能体的下一步动作会占据障碍物或者其他智能体的位置，它将保持当前位置不变。如果智能体到达指定的目标点，它将不再继续移动。

编队控制问题是指智能体从各自的起点出发，需要避开随机产生的障碍物，在短时间内到达最终目标点，并形成指定的队形。智能体的起始点随机设置在地图的四周，而目标区域则是位于地图的中间区域。

在文中，多智能体编队控制问题是一个具有马尔科夫性质的连续决策问题，因此把它建模成一个强化学习问题。文中将二维离散网格左下角的点作为原点，记为(,)，每个智能体∈{,,…，}获取当前坐标(,)作为当前状态。当智能体在户外时，通过GPS定位技术获得其他智能体的相对位置。

在文中，将智能体在二维网格地图里的动作空间集合设置为{,,,}，其中表示向上(,+1)，表示向下(,-1)，表示向左(-1,)，表示向右(+1,)。

2 改进的强化学习算法

2.1 基本强化学习算法

在强化学习算法中，智能体可以不断地与周围环境进行试错交互，使长期累积奖励最大化，并将环境的反馈作为输入。在整个强化学习与周围环境的持续交互过程中，智能体的正确行为受到奖励，错误行为受到惩罚。强化学习的目的是获得一个最优策略，使智能体可以根据策略和当前环境选择一个最优的行动，使累积回报最大化。

累积回报表示为每一时刻回报的总和，表示为：

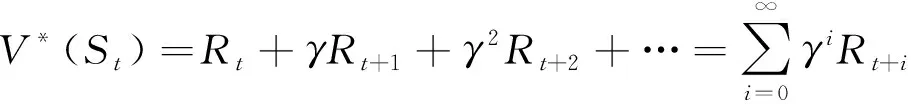
(1)

表示智能体的内部状态，表示通过执行动作之后获得的奖励，∈(0,1]表示折扣因子。

Q-learning是一种经典的基于表的强化学习算法。它将状态和动作映射到一个动作值函数中去存储值，然后根据值选择动作以获得最大奖励。动作值为(,)，即在某一个时刻环境状态∈下，智能体通过执行动作∈能够获得的最大奖赏值。在Q-learning算法中，每个智能体通过下式来更新其值：

(,)=(1-)(,)+[+max(+1,)]

(2)

∈(0,1]表示学习率。

2.2 基于群体的强化学习算法

在强化学习中，智能体是通过试错的方式学习策略的，因此获得最优策略需要花费大量的计算时间，特别是对于复杂的学习问题。遗传算法、粒子群优化算法、蚁群算法等基于群体的算法可以在广阔的求解空间下快速找到多模态函数的全局最优解。因此，文中致力于结合基于群体的算法和强化学习的算法，能够快速获得复杂学习问题的最优解。

通常，强化学习目标是寻找最优策略满足下式：

=argmax()

(3)

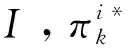
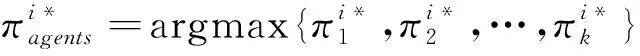
(4)

为了设计更合理的奖惩机制以有效引导智能体到达各自指定的目标点，以形成不同的队形，进而能够形成不同的形态来解决不同复杂的任务。文中引入曼哈顿距离，将作为奖赏值，奖励下一步动作能够离指定目标点更近的智能体，如下式：

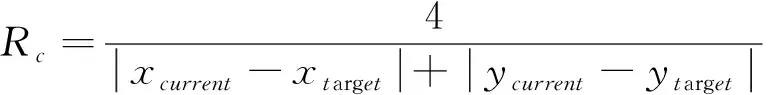
(5)

到达各自指定目标点的智能体将不再移动，并且会获得100的奖赏值。

2.3 知识共享算法

Q-learning是一种无模型的强化学习算法，通过环境的反馈为智能体的状态和行为构造一个奖励值。在奖惩机制的作用下，正确行为的Q值增大，错误行为的Q值减小，使智能体的行为趋于最优。因此，每个智能体可以选择从起点到目标点的最优路径。然而，传统的Q-learning算法仍然存在以下缺点：

(1)存储空间要求大；

(2)训练时间太长；

(3)收敛到最优解的速度很慢。

在本文的算法中，不同智能体之间可以交换它们获得的周围环境信息，即知识共享。为了缓解上述的问题，文献[19]提出了基于知识共享的Q-learning策略来实现学习不同智能体之间进行信息交互。文献[20]进一步提出了一种基于环境知识共享的群体Q-learning算法(SQL-SIE)来加速算法的收敛。然而，在智能体进行多次队形转换的场景中使用这种算法时，需要经过多次训练，才能让智能体学到形成不同队形的策略，这会耗费大量的运行时间。为了缓解这种问题，受群体强化学习算法和知识共享算法的启发，本文提出一种两阶段强化学习算法。

2.4 两阶段强化学习算法

在现实世界中，人们倾向于将一个复杂的任务分解成几个简单的子任务，以不同的方式解决它们，然后将它们有机地组合在一起。在解决了这些简单的子任务之后，更容易将获得的知识构件转移到其他复杂的问题上。文献[20]将仿真环境分解为基础区域和目标区域，还将训练过程分解为两个阶段，以此加快算法的收敛速度。受上述工作的启发，本文将仿真环境分解为基础区域和目标区域，将每个智能体看作一个独立的个体，并行执行训练，同时将算法的训练过程分解为如下两个阶段：

(1)利用基于群体和知识共享的Q-learning训练所有智能体前往网格地图的中心点，以获得一个包含全局地图信息的最优共享Q表；

(2)智能体根据这个最优共享Q表和当前所处的位置，通过避开障碍物，寻找前往指定目标点的最优路径，形成指定的队形，进而能够形成不同的形态来解决不同复杂的任务。

基于以上两阶段强化学习算法的训练过程，智能体可以将获取到的周围环境信息进行融合，形成一个最优共享Q表。通过这个最优共享Q表，智能体能够及时更新它们自身的学习策略，选择更优的下一步动作。因此，在一些复杂的学习环境中，智能体通过知识共享算法快速获取周围环境信息以获得最优策略。

3 仿真实验与分析

本文将文献[20]中的SQL-SIE算法作为一个基准算法，通过两个数值实验来验证文中算法的性能。第一个实验是使用文中算法和SQL-SIE算法分别训练12、16和20个智能体自主寻找从起始点到指定目标点的无碰撞路径，以形成矩形的队形，并统计所有智能体总的探索步数。第二个实验是使用文中算法和SQL-SIE算法分别训练12、16和20个智能体从矩形队形转换为十字队形，并统计整个程序的运行时间。

3.1 相关参数设置

在以下数值实验中，仿真环境是一个二维离散网格地图，地图四周随机出现的智能体的数量为，对应着出现在目标区域的目标点数量为。文中所有的实验都是在台式机上完成的，配置为Intel i9-9900K CPU和内存为16GB，以MATLAB2019b编写代码。

为了测试文中提出算法的性能，随机设置占网格地图面积20%的障碍物，仿真环境如图2所示。蓝色圆圈是智能体，粉色正方形是随机生成且不占据智能体位置的障碍物，目标区域是黑色菱形围成的区域。

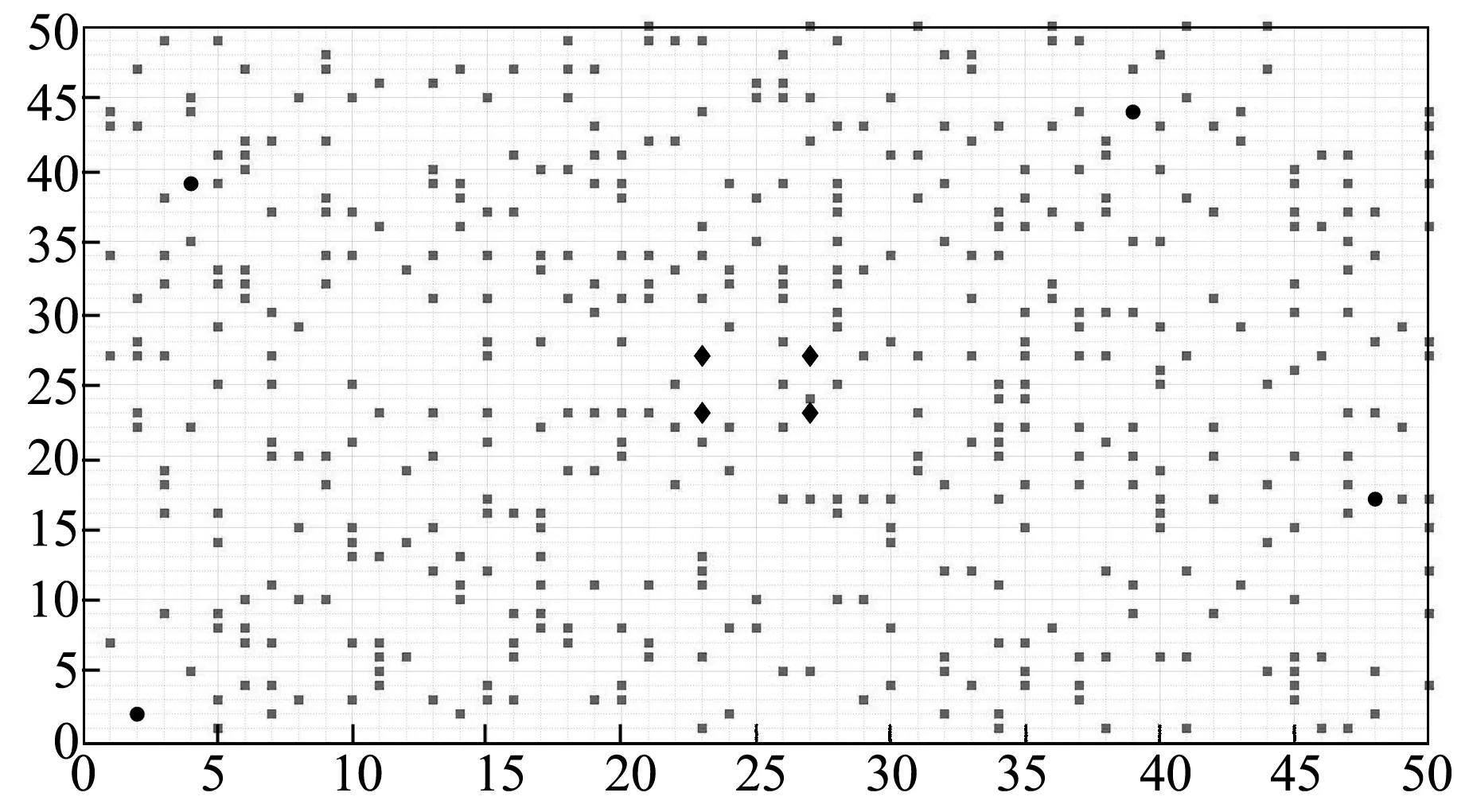
图2 二维离散网格仿真环境

实验中所有算法用到的参数如表1所示。的初始值为1。每次迭代更新之后，的值则变为当前值的0.5%，以加快贪心策略的实施。只有当所有的智能体都到达各自指定的目标点时，一次迭代更新才算成功完成。在每次迭代更新中，当智能体的探索步数超过2000，且不是所有的智能体都达到各自指定的目标点时，则当前迭代更新被认为是失败的。文中所有数值实验的迭代次数的上限是3500，将最后一个智能体到达目标点的探索步数作为衡量完成编队控制任务的指标。学习率表示智能体对新知识的接受程度，折现因子表示未来奖励的重要程度。

表1 相关参数

3.2 矩形队形

在这个实验中，多智能体编队控制任务是按照预先设定的规则，自主寻找从起始点到指定目标点的一组无碰撞路径，以形成矩形的队形。为了使文中的算法研究更具意义和通用性，在网格地图的目标区域内也设置随机障碍物，同时分别训练12、16和20个智能体来完成编队控制任务，并统计所有智能体总的探索步数。在本实验中，文中算法的训练过程如下所示：

(1)多智能体随机地出现在二维网格地图四周；

(2)使用两阶段强化学习算法训练多智能体，通过避开障碍物，到达地图的中心点，生成最优共享Q表；

(3)基于这个最优共享Q表，智能体从中心点出发，到达各自指定的目标点，以形成矩形队形。

图3～图5是将50×50网格地图获得的数据，经过平滑处理后的结果(连续50个数取均值)，文中算法的收敛速度比SQL-SIE算法快，智能体总的探索步数更少。

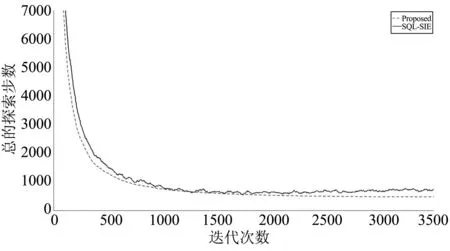
图3 训练12个智能体的编队控制结果对比

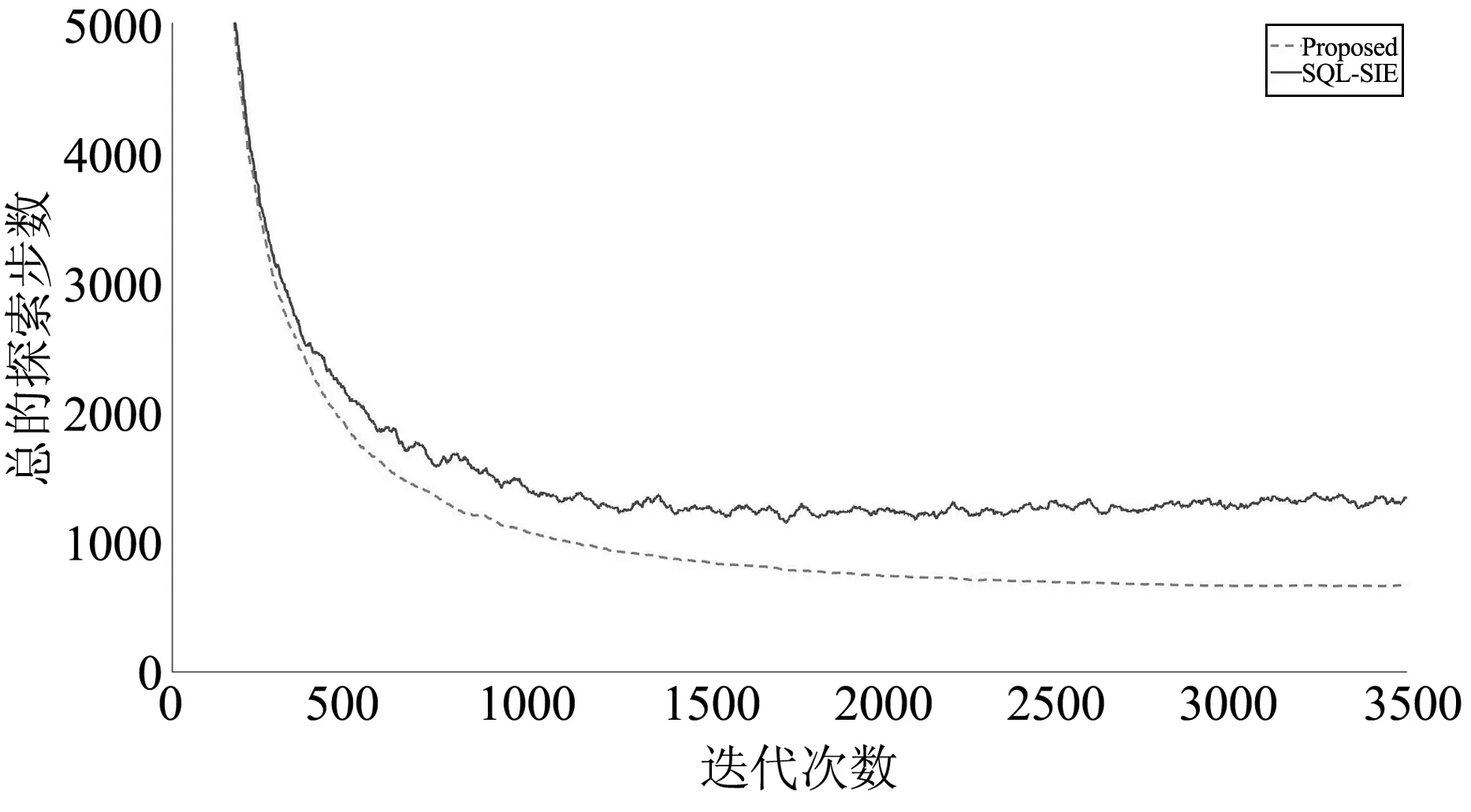
图4 训练16个智能体的编队控制结果对比

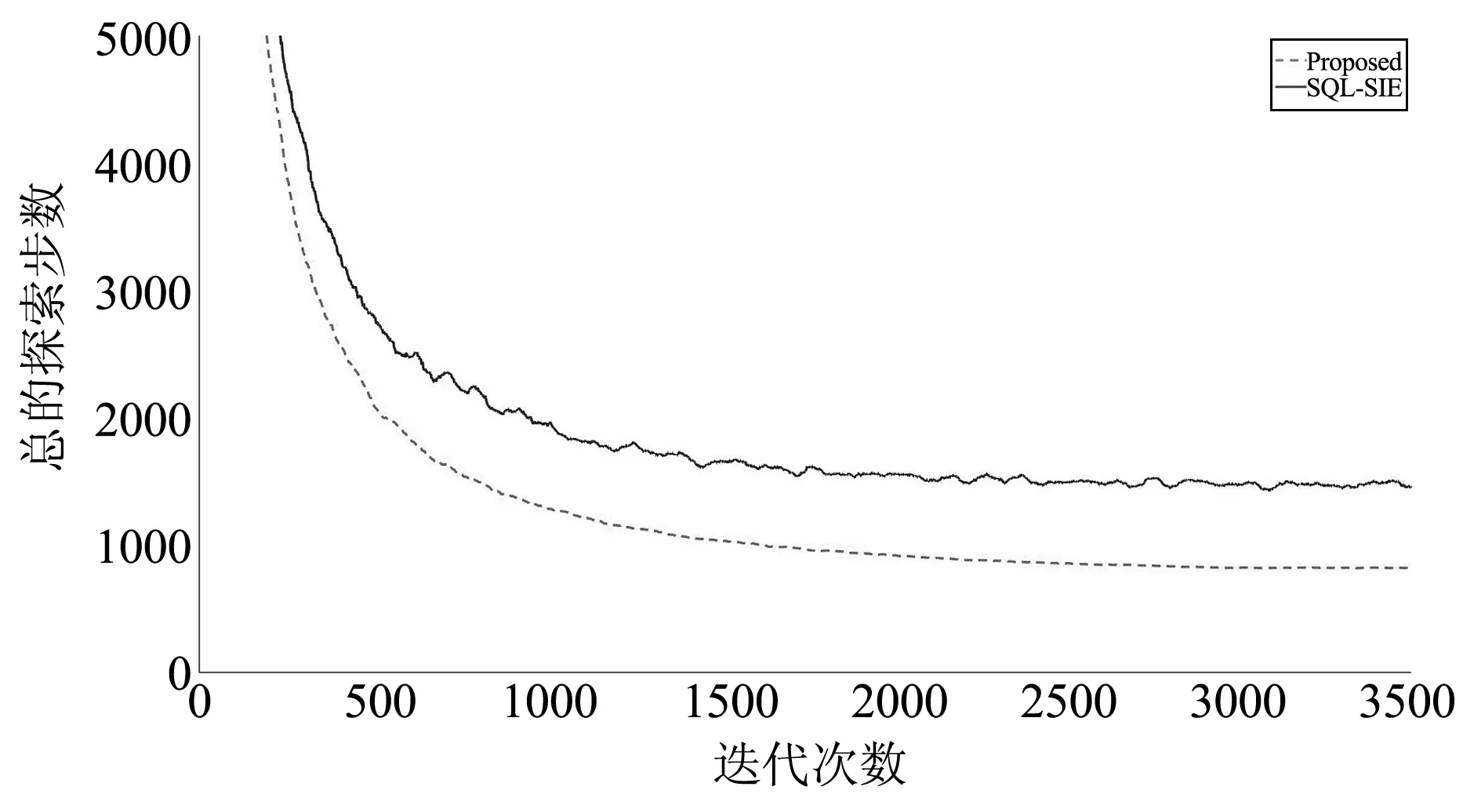
图5 训练20个智能体的编队控制结果对比

在基于群体的强化学习和知识共享算法的作用下，本文算法融合所有智能体周围的环境信息，将环境信息存储为一个共享的Q表，并将共享的Q表传递给每个智能体。智能体得到这个共享Q表之后，及时更新自己的Q表。基于更新后的Q表，智能体根据当前所处的环境位置以获得更好的下一步行动和更大的奖励值，加快算法的收敛速度。此外，由于本文算法的第一阶段是训练分布在地图四周的智能体移动到地图的中心，因此智能体获得比SQL-SIE算法更全面的地图信息。通过上述过程，智能体得到最优的共享Q表，得到从地图上任意一点移动到另一点的最优路径。

当在50×50和100×100的网格地图上使用文中算法分别训练12、16和20个智能体时，所有智能体在3000迭代次数后都能获得到达各自指定目标点的最优路径。然而，使用SQL-SIE算法训练同样的智能体在100×100的网格地图中获得前往指定目标点的最优策略时，超过一半的智能体不能到达各自指定的目标点。根本原因是实验环境是一个有限大小的二维离散网格图，智能体必须避开路上的障碍物，而且在该算法的障碍物设定中，先到达各自指定目标点的智能体被其他未到达的智能体视为障碍物，其他智能体要避开这些障碍物。因此，一些智能体在前往其指定目标点的途中会受到上述两种障碍物的阻碍而导致智能体无法继续移动。而本文算法是先训练智能体到达地图的中心点，则不会出现以上的情形。此外，在SQL-SIE算法的奖励设置中，只有当智能体碰到障碍物或到达目标区域时，智能体才能获得奖励。然而，从起始点到目标点，没有适当的奖励引导智能体向有利于到达目标点的方向移动，导致了出现稀疏奖励的问题，容易出现在障碍物附近来回走动的现象，使得算法难以收敛到稳定状态。为了解决上述问题，本文算法将式(2)奖励给下一步动作距离各自指定目标点更近的智能体。这个奖惩机制能够引导智能体以最小的探索步数移动到各自指定的目标点，加快算法的收敛速度。

规定智能体在每个迭代次数中的最大探索步数为2000，如果智能体在当前迭代次数中花费超过2000探索步数都无法到达其指定的目标点，2000就作为该智能体到达目标点的最大探索步数。如表2所示，与SQL-SIE算法相比，在50×50的网格地图中，本文算法训练智能体到达指定目标点所需要的总的探索步数要少将近50%。

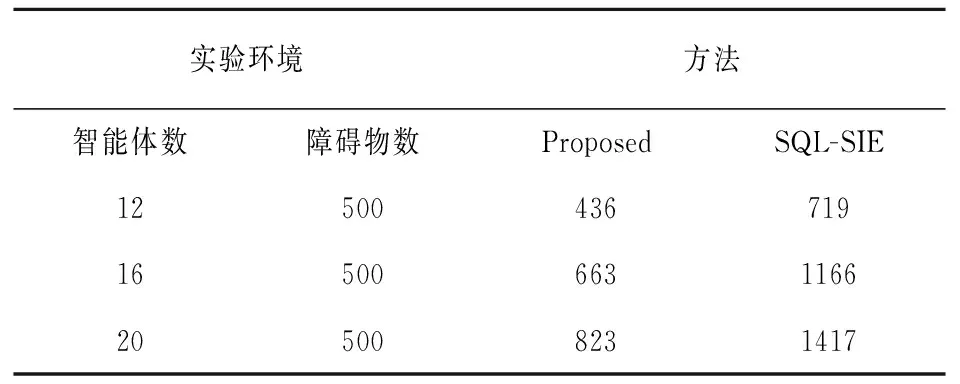
表2 50×50网格环境总的探索步数

在有限大小的二维网格环境和有限迭代次数的情况下，随着智能体数量的增加，本文算法的优势更加突出。这是因为随着智能体数量的增加，智能体通过知识共享可以更快、更全面地获取全局信息。事实上，使用文中算法训练智能体可以得到去往目标点的最优路径，而使用SQL-SIE算法训练则不能得到最优路径。此外，如表3所示，在100×100的网格地图中，当使用SQL-SIE算法训练智能体时，由于存在稀疏奖励的问题，超过一半的智能体不能到达指定的目标点。因此，当使用文中算法训练智能体移动到各自的目标点时，得到总的探索步数将远小于使用SQL-SIE算法得出总的探索步数，并且随着智能体数量的增加，这个差距会变得更加显著。

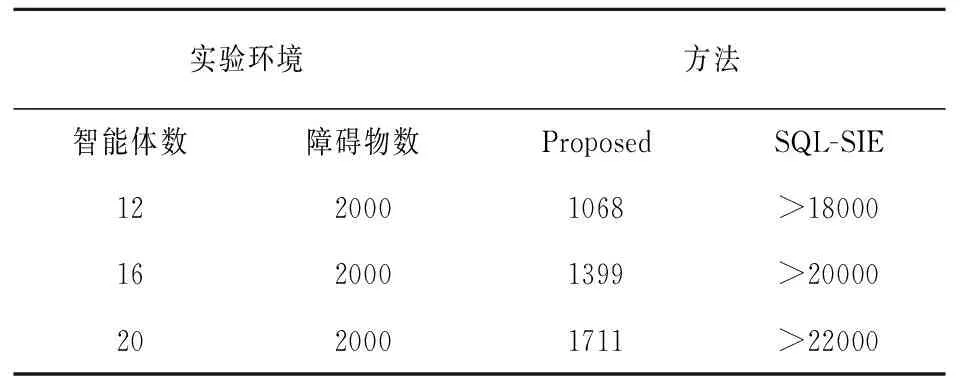
表3 100×100网格环境总的探索步数

3.3 队形转换

为了验证本文算法在多智能体进行队形转换的性能要优于SQL-SIE算法，文中设计这个实验分别训练12、16和20个智能体来完成队形转换的任务，并统计从矩形队形转换到十字队形所需要的运行时间。本文算法的训练过程如下：

(1)训练网格地图四周的智能体通过避开障碍物，到达网格地图的中心点，并生成最优共享Q表；

(2)智能体根据上述的最优共享Q表，从中心点移动到各自指定的目标点，形成矩形队形；

(3)继续沿用上述的最优共享Q表，智能体从矩形队形上的目标点继续移动到另一组指定的目标点，形成十字队形。

同时，本实验使用SQL-SIE算法来完成编队转换任务。该任务的训练过程主要分为两个阶段：第一阶段是训练智能体从地图的四边移动到地图的中心区域形成矩形队形。第二阶段是训练智能体从矩形队形转换为十字队形。统计上述两种算法中所有智能体完成队形转换任务所需的运行时间。

如表4所示，在50×50的网格地图中，使用文中算法完成队形转换任务的运行时间比使用SQL-SIE算法快将近5倍。因为文中算法的第一阶段是训练分布在地图周围的智能体，使其移动到地图的中心，因此智能体可以获得比SQL-SIE算法更全面的地图信息，从而获得最优的Q表。此外，智能体经过第一阶段的训练后，可以得到全地图的环境信息融合而成的Q表，因此可以减少智能体的随机试错次数，从而加快算法的收敛速度。通过使用这个最优Q表，智能体可以得到从地图上任意一点移动到另一点的最优路径。智能体在转换队形时不需要再进行训练，只需要根据Q表和当前所处的位置执行下一步动作。因此，当智能体从矩形队形转换为十字队形时，只需要根据Q表和当前所处的位置移动到十字队形上各自指定的目标点，即可快速完成队形转换任务。

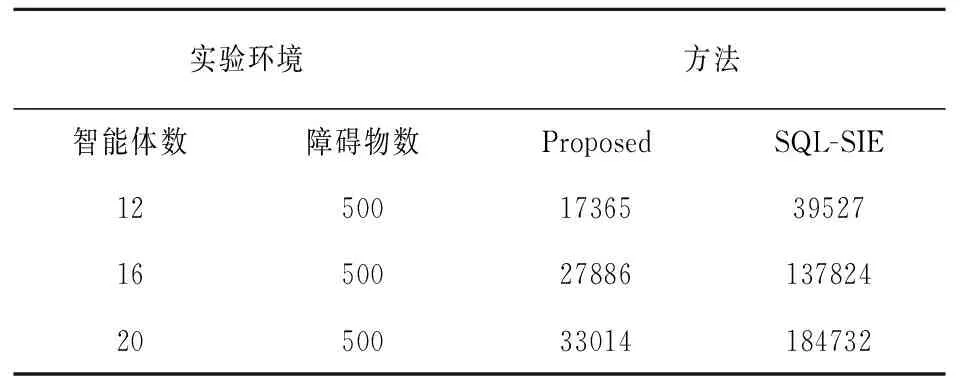
表4 50×50网格环境运行时间(s)

如表5所示，在100×100网格地图中，使用SQL-SIE算法不能分别训练12、16和20个智能体形成矩形队形，更不能完成队形转换任务，因此本文将100×100网格地图下使用SQL-SIE算法训练智能体完成队形转换任务的运行时间表示为无穷大。

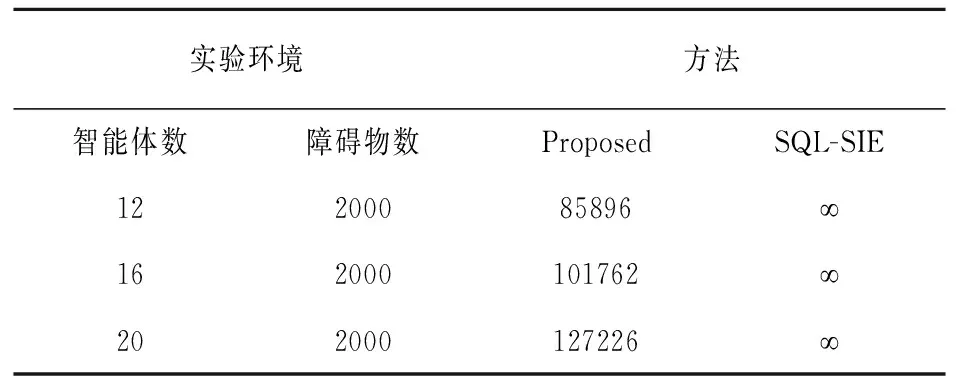
表5 100×100网格环境运行时间(s)

4 结 论

将模块化机器人编队控制建模成一个多智能体强化学习问题进行研究。本文研究每个智能体都学习一种最优的策略，通过避开障碍物，在最短的时间内移动到目标点和形成特定的队形，以完成编队控制任务。本文还研究将多智能体从矩形队形转换成十字队形的编队控制问题。在基于群体和知识共享的基础上，提出了两阶段强化学习算法。在第一阶段，使用基于群体的强化学习算法和知识共享的算法训练智能体避开随机产生的障碍物，寻找到达中心点的最优路径。由于这个阶段是训练地图四周的智能体从起始点前往中心点，为了能够减小稀疏奖励的影响，设计适当的奖励引导智能体向有利于到达中心点的方向移动，从而减少算法迭代次数，提高算法的收敛速度，文中引入了曼哈顿距离作为奖赏值。因此通过这个阶段能够获得较为全面的地图信息，即能得到地图上任意一点移动到另一点的最优路径。在第二阶段，利用第一阶段获得的最优共享Q表，训练智能体从中心点移动到各自指定的目标点，完成编队任务。在这个阶段中，当智能体进行多次队形转换时，不需要多次训练，只需根据最优共享Q表和所处位置，移动到各自指定目标点。实验结果表明，该算法具有较好的性能。主要表现在算法收敛速度较快，智能体实现队形转换任务需要的时间较短，具有良好的实用性。