∑-Δ模数转换器在数字万用表专用芯片中的应用研究
居水荣,王津飞
(江苏信息职业技术学院 微电子学院,江苏 无锡 214153)
数字万用表(Digital Multimeters,DMM)是电子电机人员不可缺的设备,其中的核心部件为一颗模拟前端(Analog Front End)DMM专用芯片,内含高精度的∑-Δ模数转换器(Sigma-Delta ADC)。
∑-Δ模数转换器通常是在低采样率下进行高精度的数据转换,通常精度可以达到20位以上;跟其他类型的ADC相比其成本较低,并且有相对较高的稳定性、较低的功耗。
本文将对∑-Δ模数转换器工作原理进行分析,并详细介绍其在DMM芯片中的应用。
1 ∑-Δ调制器工作原理
任何模数转换器都包括3个基本的功能,即抽样、量化与编码。抽样过程将模拟信号在时间上离散化使之变成抽样信号,量化将抽样信号的幅度离散化使之变成数字信号,编码则将数字信号最终表示成为数字系统所能接受的形式与性能。
∑-Δ调制器并不是直接根据抽样数据的每个样值的大小进行量化编码,而是根据前一样值与后一样值之差即所谓增量的大小来进行量化编码,在某种意义上其是根据模拟信号波形的包络形状来进行量化编码,而且由于在调制器前端增加了起累加作用的积分器,因而称其为总和增量调制器。总和增量调制器由2部分组成,第一部分为模拟∑-Δ调制器,第二部分为梳状数字抽取滤波器。∑-Δ调制器是核心部分。
与传统的A/D转换器相比,增量调制型A/D转换器实际上是采用以高抽样频率,比奈奎斯特抽样频率大许多倍,称为过抽样。低的量化位数是以高的过抽样率为代价换来的,即以速度来换精度的方案。
为更清楚了解Sigma-Delta ADC的工作原理,下面以一阶Sigma-Delta调制器来进行详细分析。
图1(a)为一阶Sigma-Delta调制器的系统原理图,图1(b)为对应线性Z域模型;其中x(n)到y(n)之间的累加迭代部分相当于积分器,后级的ADC在量化过程中引入量化误差e(n),反馈回路中的DAC电容在反馈数字量化信息时需要延时处理。
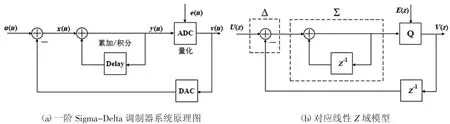
图1 一阶Sigma-Delta调制器原理分析示意图
图1中,u(n)为输入信号,v(n)为输出信号,根据图1中的信号流可以得到
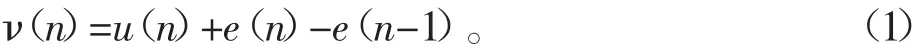
由式(1)可以看出,输出信号v的值为输入信号u加上当前量化误差e(n)和上次量化误差e(n-1)的差值;公式(1)的Z域系统函数为
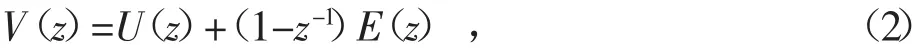
式中:V(z)为Z域输出信号;U(z)为Z域输入信号;E(z)为Z域的量化误差信号。
式(2)可以改写为

式中:TFs为输入信号传输函数;TFn为量化误差信号传输函数;对于一阶Sigma-Delta结构,TFs为单位增益1,TFn为(1-z-1)。
对于图1所示的一阶Sigma-Delta来说,其噪声能量分布如图2所示。

图2 一阶Sigma-Delta的噪声能量分布
由图2的噪声传输曲线可以看出,是典型的高通滤波,即对低频分量能够起到衰减的作用。
最终计算出这种一阶Sigma-Delta ADC的最大信噪比为

式中:SNR为信噪比;ENOB为环路量化器的有效位数;OSR为过采样速率。从该式可以看出,当过采样率为2时,信噪比可以提高到9.03 dB;另外,公式中有效位数的提高值可以表示为

由式(5)可以看出,过采样率OSR每次翻倍,有效位数ENOB可以提高1.5位。
对于普通的奈奎斯特ADC来说,过采样技术同样可以提高有效位数,即
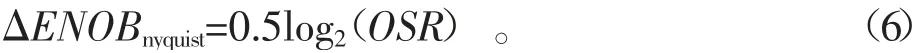
比较式(5)和式(6)可以看出,对于同样的过采样率,一阶Sigma-Delta调制可以获得更高的转换精度;同时所设置的过采样率越高,提升的转换精度也越高,但所牺牲的带宽也越大。因此对于Sigma-Delta调制器的设计来说主要需要考虑的是带宽和精度的折中,这也是在仅考虑精度的Sigma-Delta ADC中往往采用高阶环路调制的原因。当然在这类ADC中需要更多地考虑低频噪声的压制,从而减小带宽的损耗;并且这类ADC往往需要更多环路运放,会带来更大的功耗。
2 应用于数字万用表芯片中的Sigma-Delta ADC
2.1主信号流分析
Σ-Δ调制器中的信号流分析如图3所示。
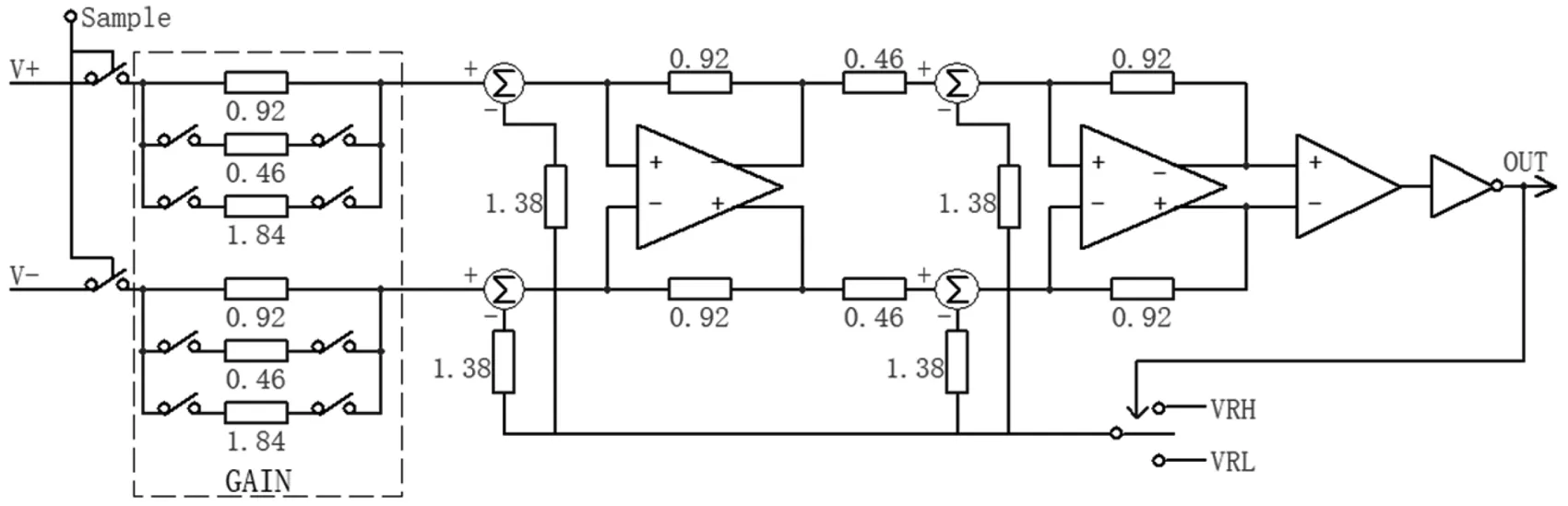
图3 Σ-Δ调制器中的信号流分析示意图
V+与V-分别为电压通道的正负输入端,对外部供电线路进行采样后得到的电压信号Sample由此输入端接入电压通道。信号首先进入采样部分。由于DMM芯片采用的是Σ-Δ模数转换器。它属于增量调制编码器,对于频率越高的信号,其产生不过载量化失真的幅度就越小。当Δ一定时,为了提高最大临界过载振幅,尽量提高抽样频率,即提高过抽样比(在此应用中,信号频率相对稳定)。本文DMM芯片中采用的过抽样频率为40 kHz,即每隔25 μs对信号采样一次,已满足对用电线路电压电流变化情况的采样要求,而不会产生过大的失真。采样过的信号经过±Δ电路部分进入由2个运算放大器以及电阻与电容构成的插入网络中。由本文前面的分析中可知,用插入网络代替由多个积分器级联的部分。这样可以将Σ-Δ调制器的分析与设计问题变为对线性滤波网络即H(z)的分析与设计,使电路的设计变得更加灵活。对于本文DMM芯片中的插入网络,稍后进行分析并推导其传输函数。由插入网络输出的信号送入比较器,用于判断此时为了跟随输入信号的变化是需要加还是减一个Δ(用回路中的开关代表)。然后将信号反馈给前面的±Δ部分进行合成。至此,完成了Σ-Δ转换器的将输入的模拟信号转变为1 bit量化信号的功能。
2.2开关电容积分器
Σ-Δ调制器采用开关电容网络来构成积分器,如图4所示,是一种很常见的结构。
在采样模式下,图4中开关S1和S3闭合,S2和S4断开,电容C1两端电压跟踪VIN,此时运放和电容C2保持前值。在向积分模式转换过程中,S3首先断开,向C1上注入固定的电荷,S1接着断开,随后S2和S4导通,C1上的电荷传到C2。
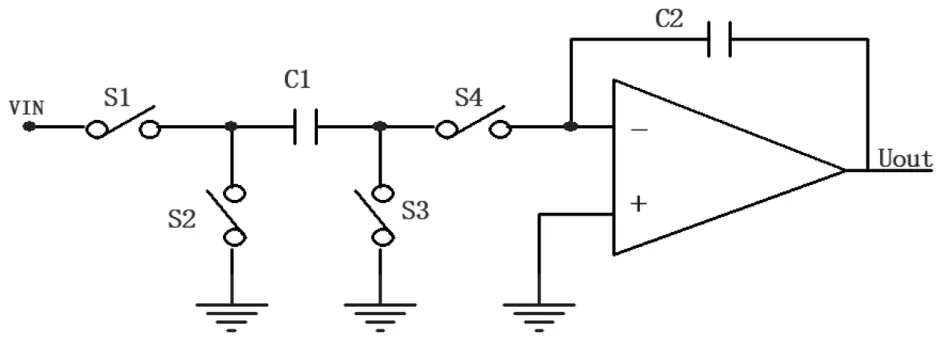
图4 开关电容积分器图
电路从采样到积分转换过程中,因为S3首先断开,所以它只引入了固定的失调电压并可以通过差动电路消除。此外,因为C1的左极板是“被驱动”的,所以S1和S2的电荷注入或吸收不会引起误差。上述开关时序如图5所示。
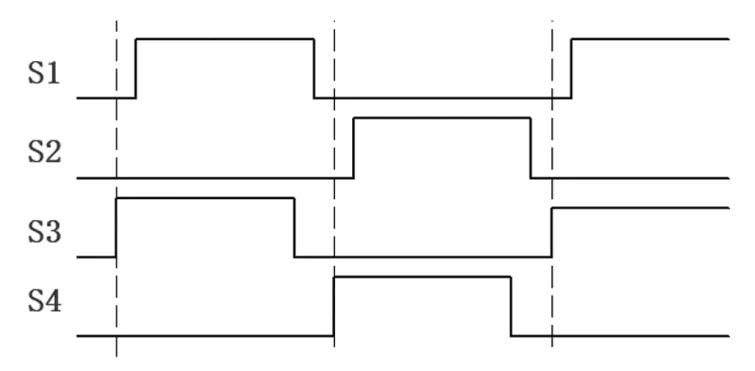
图5 开关电容积分器中的开关时序
2.3一位模数转换
此电路的作用是将前面插入网络处理后的信号进行比较产生一个控制信号,并由此把不同的电压信号转换为不同占空比的数字信号,其结构如图6所示。电路是一个两级互补型MOS(CMOS)运放,第一级是一个P沟道MOS(PMOS)交叉耦合灵敏放大器,第二级是一个PMOS共源放大器。

图6 1 bit模数转换器电路结构
在读出数据前,先使开关闭合,第一级运放两个输出短接,造成初始平衡;而在读出数据时,开关断开,2个输入所出现的电平差,通过交叉耦合正反馈作用,使输入电平低的一端被拉至“1”,而电平高的一端被拉至“0”,从而实现了把小电平差放大的功能,放大后的信号单端输出,再经过单管二次放大,最后数据写入锁存器。
2.4±Δ电路的分析
由比较器输出的信号控制±Δ电路。此电路为一开关电容网络,简化图如图7所示。
对于图7中上半部分的支路一,电容C1两端电压VC1=VIN+(VREF-AGND)。
对于图7中下半部分的支路二,若S1=S5,S2=S5N,则电容C2两端的电压VC2=0,电路执行-Δ功能;若S2=S5,S1=S5N,则电容C2两端的电压VC2=VREF+(VREF-AGND),电路执行+Δ功能。
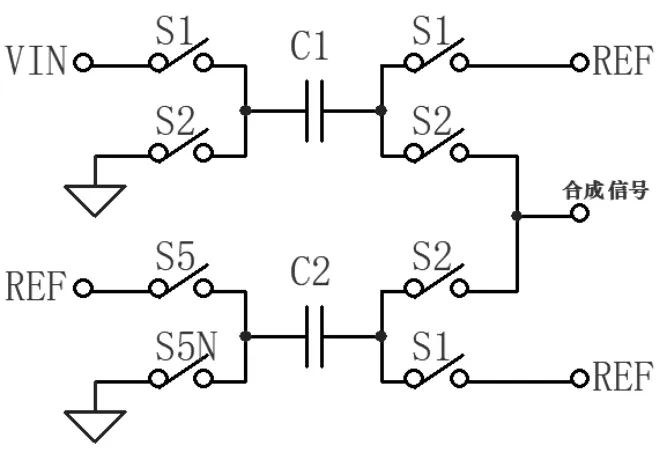
图7 ±Δ电路简化图
2.5 ADC中的低通滤波
输入信号将送到ADC里被采样。如果输入信号上叠加了一个比采样频率高得多的噪声,那么在通过采样电路后会产生一个低频噪声。因此建议让输入信号经过一个低通滤波器,以期得到稳定的ADC输出。低通滤波器的构成及相关控制信号如图8所示。
本文研究的DMM芯片内部有1个100 kΩ的电阻,其与外部连接于FTB和FTC之间的一个电容(10~50 nF)构成低通滤波器,该电容取值一般在10~50 nF之间,电容过大将导致在输入信号切换时引起太大延时。图8中的控制信号SFT<2>决定输入信号是否通过低通滤波器。
2.6 ADC中的数字梳状滤波器
由前文可知,∑-ΔADC包括∑-Δ调制器和数字梳状滤波器2部分。在图8中,当控制信号ADEN=1时,∑-Δ调制器开始工作。当ADRST=1时,梳状滤波器使能;当ADRST=0时,梳状滤波器被复位。

图8 低通滤波器的构成
数字梳状滤波器结构如图9所示。

图9 数字梳状滤波器结构
3 结论
以一阶∑-Δ调制器为例,本文介绍了∑-ΔADC的工作原理和设计指标优化,并对应用在数字万用表DMM芯片中∑-ΔADC的信号流程、各核心模块电路结构等内容进行了详细描述,为读者设计和使用这一类ADC提供了参考方案。

