“直观模型”在小学数学学习中的价值追问
——兼谈“分数乘分数”的直观图示
□刘加霞
运用“直观模型”①直观模型指小棒、计数器、平面图形及其面积图、线段图或者数线等直观材料。其本质重在“几何直观”而非“模型思想”。直观模型叫“直观示意图”更恰当,或者叫“直观图示”,叫“直观图式”则不妥。图式(schema)是哲学或者认知心理学中的专有名词,有特定含义。似乎是小学阶段学习运算意义、理解算理的“必备武器”,即计算教学中一直强调的“直观模型是帮助学生理解算理的一种重要方式”[1]。直观模型一定有助于学生理解算理吗?学生读懂“直观模型”本身是否就很难?测评时要求学生“画图表示计算的过程和结果”是否是高水平抑或是“无理”要求?如何对学生的“图画作品”进行评分呢?再进一步追问,直观模型的育人价值到底是什么?教师在教学中如何辩证地使用直观模型?这一系列问题需要结合案例条分缕析地解释和说明。
一、引子:“画图表示计算过程与结果”适合纸笔测评吗?
下面是某地区六年级期末检测的一道题以及对某学生作答的评分情况(如图1)。某学校教学主任向笔者“求救”:
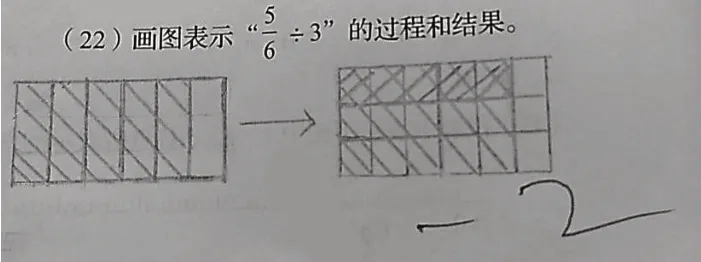
图1
老师,我的同事问我“为啥要扣2分”?(满分4分)
同事们又追问我“题目中不是让‘画图’表示吗,为啥要写出分数的“数字符号”?学生理解题意没错呀”。
该主任无奈地问我:老师,我该怎么解释呀?老师们“打起来”了。
过了一段时间该主任又问我:老师,下面这道题(如图2)该不该扣分?我觉得应该扣分,但领导说“别扣分了”。我彻底糊涂了!
如何解决该主任的困惑与“痛苦”呢?为何“不应该扣分的却扣分,应该扣分的却不扣分”呢?第二题学生的作答显然要扣分的,因为没有“直观表示”出“9+1”。当然,这样的“题目”适合作为纸笔作业或测评任务吗?是否是领导意识到不应该用“画一画你的计算过程”这样的问题来“难为学生”,所以学生画成图2那样也不扣分?

图2
对于第一个问题是否扣分争议确实很大。通过对一线教师进行调研,发现他们的答案主要有三类即刘晓婷[2]文中的前三种,几乎没有后三种。也就是说一线教师的答案跟该学生的答案基本一致,看来教师作答该题也很难得到“满分”。到底如何“画图”,连教师“都有不同观点”甚至“都拿不准”,为何要测评学生呢?即使测评了,哪种画法算是“标准答案”呢?如何制定“宽容的”评分规则呢?
画直观图示的根本目的是什么呢?用“直观图”表示计算过程与结果对学生而言是“容易”还是“更困难”?操作“直观模型”得到计算结果本身是一种算法,既然“允许算法多样化”,那为何要求所有的学生都会“画图”呢?这是否是小学数学教育悖论?如此看来,需要进一步追问“直观模型”是什么、承载哪些价值。
二、追问:“直观模型”是什么?价值何在?
(一)什么是直观模型?
如前所述,直观模型是各类直观的、有结构或无结构的可视化材料,具体指小棒、计数器、平面图形及其面积图、线段图、数线等直观材料。运用直观模型是指用“画图、列表”等可视化方式“表示”出思考过程、数学知识内涵和问题解决过程的手段。既然是“表示”,不同的人就有不同的表示方法,即有“人为约定”的成分。例如,关于分数乘分数,人教版教材六年级上册[3]中采用图3中的表示方法,北师大版教材五年级下册[4]中采用图4中的表示方法,都能直观解释其运算意义、计算过程与结果,不能说“谁对、谁错”,各有其合理性。

图4
北师大版教材“分数乘分数的情境”中,没有具体的数量,第一个因数表示“阴影部分占整个图形的(用虚线表示平均分4份)”,“阴影”与“整个图形”都是“客观存在”,再将其“平均分4份”,必然是“阴影”与“整个图形”同时被“平均分4份”,用“实线”表示第二次“平均分4份”的过程。
之所以阐述上述内容,只想强调当脱离现实情境,用“画图”表示“分数乘分数”时,没必要纠缠用“实线”还是“虚线”表示平均分、第二次平均分一定要先“平均分阴影部分”再“平均分整体”,也就不能说只有像人教版教材那样画图才算“正确”,而北师大版教材那样画图是“错误”,实际教学中一定不用“严格”区分这些不同的画图方法。只要学生的“思考过程”是正确的就行,毕竟画图有“约定成分”,不同的“直观图示”可能表示了“相同的思考过程”,不存在唯一正确的“图示”。如果将“画图”作为考试内容来检测学习效果,评分规则一定要遵循“宽容原则”,画出图1的学生不应该被扣2分。
用直观模型表示能揭示“运算本质”吗?显然不能。它只是理解运算意义、算法与算理的表征方式之一,还有其他不同的表征方式。例如,巩子坤[6]提出分数乘除法运算有三种表征方式:直观表征、抽象表征、形式表征。直观模型或直观图示是表征计算过程的方式之一,它首先是一种直观表征,当学生能够借助直观操作(直观图示)解释、说明计算的道理可称之为“借助直观模型理解算理”。如果学生没有“解释、说明计算道理”的行为,只是根据数的意义、运算的意义而画出直观图示、通过“计数”得到计算结果,这时的直观操作就是一种算法。
每种直观模型各有其现实情境背景,又有“约定”的成分,为何非让学生“洞察”到各种不同直观图示的差别甚至判断出“谁对、谁错”呢?即使通过训练学生能够掌握各种“画图”,但有必要吗?因为理解运算的意义、算法与算理本来就有不同的方式或途径,直观模型只是其中的一种,是“手段”不是“目的”,教育中把“手段”当作“目的”岂不是“本末倒置、南辕北辙”?
(二)直观模型对小学生学习数学的价值
使用直观模型能够将学生“内隐的”思考“外显化”,便于学习过程中的交流讨论与分享,这一点已为广大教师所认同。它的另外两方面价值也需要广大教师关注和了解。
1.通过“计数”直观材料获得正确的计算结果是算法多样化的根本保证
四则运算源于“计数”,即“数出”计数单位的个数,人们对“数出”的结果“坚信不疑”,这类似于“公理”,即不再追问计数出的结果“为什么正确”。由于所有运算都是“一一映射”即“操作”两个运算对象(数)之后,能得到唯一的“数”与之对应,也就是所有运算的结果都具有唯一性。运算结果唯一性,是运算可以“算法多样化”的前提。通过不同的计算方法或方式得到的结果如果相同,就说明每一种算法都是正确的。如果某种算法与其他算法得到的结果不同,说明该算法“出错”了,需要重新计算或者检查计算过程是否是某一步骤“出错”,所谓“出错”就是违背了数或运算的意义、不符合运算的性质或定律,更可能是“看错数”即改变了运算对象。
当用不同算法得到的结果不同时,学生才有“理解算理”的需求,有借助“直观模型”检查或解释每一步计算是否正确,从而感悟到直观模型的作用。在学生已经正确计算也能够口头解释每一步的道理的基础上,要求学生“直观操作”,或者考试时专门考查“画一画计算过程”都不是数学教育所倡导的。这易导致学生厌恶数学,毕竟“画图”比“口算、列式计算”更麻烦。当然,如果是作为“过程性评价”的检测题,要求“画一画计算过程”也是必要的。
2.用直观模型“定义”分数乘法
伍鸿熙[7]认为,分数乘除法应该舍弃“现实意义”,以“定义”的方式界定分数乘法的含义。他给出了分数乘法的两个“定义”或称之为“解释”:
前述这两个定义都可以看作是分数乘法的直观模型——面积模型、数线模型,但是,目前现行的各个版本的教材中没有直接“定义”分数乘法,而是基于分数意义以及自然数乘法理解分数乘法。前述两个定义脱离现实背景,比较抽象,尤其是定义2,小学生较难理解。但是定义1特别值得借鉴,下面简要论述。
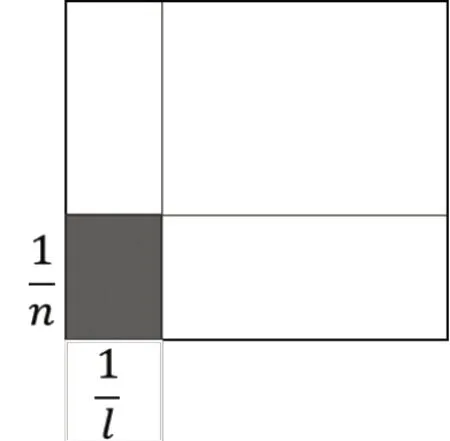
图5
再将这个“单位长方形”每行摆k个,摆这样m行,所得到的就是边长为和的矩形,它的面积是mk个“单位长方形”即,所以,就得到分数乘法的运算法则,如图6所示。
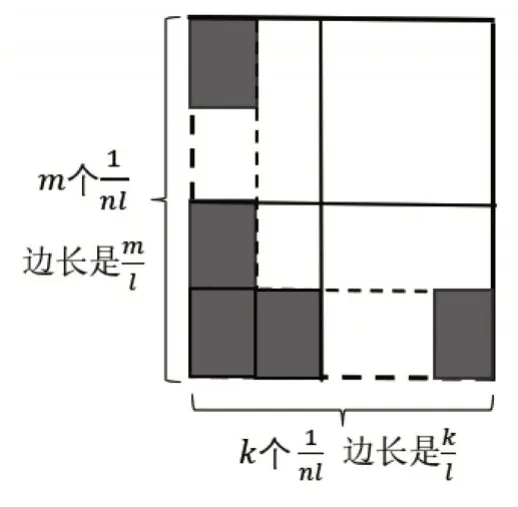
图6
虽然都用“矩形的面积”表示分数乘法,但是定义1与人教版、北师大版教材上所画的直观模型完全不一样。通俗地说,定义1是“根据定义先得到分数乘分数的新单位,再计数新单位的个数”,现行教材是“先规定‘单位1’,再根据分数意义以及自然数的乘法,理解分数乘法”。定义1是先根据分数乘法定义产生新单位,再一行一行地排列产生边长分别是和的矩形,它的面积就是的乘积。现行教材的解释则是先规定“单位1(单位正方形)”,延垂直方向将其平均分成n份,得到第一个因数,新单位是;再将按水平方向平均分l(再次得到新单位,这样的k份就是按照分数的算子含义即“的就是
伍鸿熙给出的分数乘法定义确实更为严谨、具有一般意义,可以脱离现实背景。该定义的另一个优点是先进行“分数单位乘分数单位”得到“新单位”,再计数“新单位”的个数,实现自然数、小数、分数乘法的“一致性”。定义了分数乘法之后,再根据“除法是乘法的逆运算”(运用代数推理)得到分数除法的定义以及运算法则。正如《义务教育数学课程标准(2022年版)》[8]中“例16”论证的“为什么4÷2可以写成”:首先,可以通过除法运算的意义和分数的意义理解它们之间的等价关系。其次,根据“除法是乘法的逆运算”“等式性质”以及基本事实“等量的等量相等”即可推理得到最后,根据表示相加,所以写成”,再根据“等量的等量相等”即可证明,也能得到“除以一个数等于乘这个数的倒数”。
借助直观模型根据分数意义以及除法的意义(等分除、包含除)解释分数除法的算理,还是根据“商不变的性质”或用“除法是乘法的逆运算、代数推理”的方法学习分数除法?显然,最后一种方法的推理过程非常严谨,每一步都“有根有据”,但是,小学生能否“像数学家一样思考”,到底用哪种方法学习分数乘除法等问题都需要在教学实践中进一步研究,成人不能想当然地做决定。
三、建议:要正确认识且辩证地使用直观模型
(一)辩证地看待用“直观模型”表示思考过程
布鲁纳提出学习的多元表征理论,即动作表征、表象表征与符号表征,其后Lesh批判并修正了布鲁纳的多元表征理论,将其分别改为操作模型表征、图像表征、书面符号表征,并提出口头语言表征、现实情境表征在学习过程中扮演重要角色,并提出多种表征方式的相互转换[9]。因此,学生不仅仅要能够直观表征,还能通过语言表达来描述、解释数学概念、技能、性质以及规律等。
直观模型是动作表征、表象表征的“产物”。学生会用直观模型表示自己的思考过程,读懂别人的直观模型,对他们来说都属于“较高水平”的要求。因为有时候的“直观”并不“真正的直观”而是“抽象的直观”。如“画一画9+4的计算过程”,学生通过口算知道结果,也知道可以拆分为“9+1+3=13”的凑十法,却很难画出“小棒图”表示这个计算过程。又如,各地区经常检测图7中的题目,如果没有直观“点子图”,很多学生能否回答竖式中第二个“部分积”每个数字的意义(即能够解释算理)?为何非要考查用“点子图”解释“竖式中每个数字的含义”呢?评价的目的难道是“必须用多种方式”计算?这与用“自己喜欢的方法”不是矛盾吗?
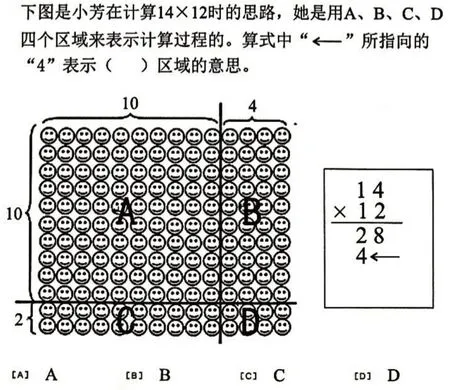
图7
学生能够用“自己喜欢的方式”理解、完成学习任务是最基本的教育目标,即用一种方式正确表达或解释即可。能够用多种表征方式表达他的理解过程,说明学生达到了“深度学习、深度理解”,是高水平思维的表现,但不能期望学生刚开始学习即能达到这个水平。
(二)“画图表示思考过程”不适合作为纸笔测评的任务或要求
如前所述,画“直观示意图”的任务不适合纸笔测评。纸笔测评时,学生画出来的都是“结果”,难以考查学生的“过程”,难道只有多画几个“图”并用“箭头”表示出“前后画图顺序”才能表明“过程”吗?只有“一幅图”,也有“画的过程(分别用实线、虚线表示)”只不过“老师没有看到”或“没有读懂学生的画法”,为何就不行呢?显然纠缠这样的“问题”不是教育的明智之举。
该类任务应该作为“表现性任务”用于课堂教学中,教师可以观察学生“画图过程”了解学生的思维步骤以及难点,直观模型将学生“内隐的”思考“外显化”,便于同伴之间、师生之间的交流探讨与经验分享。
如果非要测评学生对分数乘法的直观模型是否理解,用如下方式测评更合适:小明用下图表示了一个乘法算式的含义,这个算式是()。
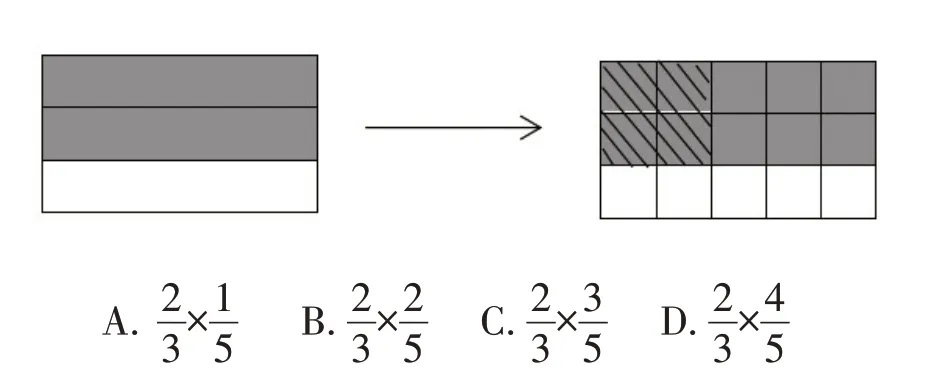
(三)随着年级的升高,直观模型应该逐步“退出”学习历程
学生对数学知识的理解有四个水平[10]:直观理解、程序理解、抽象理解与形式理解,它们是循序渐进的。由于小学生的思维是具象的、自我中心的,所以在低年级需要借助直观手段理解抽象的数学概念、原理等。但随着学生年龄增长,思维越来越抽象、结构化,数学学习应逐步舍弃直观操作、直观模型的支撑,依靠计算、几何推理、代数推理、类比迁移等方式学习数学知识、技能,解决问题。
要避免让高年级学生在低水平(前二者)上停留的时间过长的做法,更要避免明明学生已经达到“抽象理解”,却非要人为地将他们“拉回”到直观理解水平的做法。更不适合用“低理解水平”的素材来测评已处于“高理解水平”的学生,因为很多时候不是学生“不懂”数学知识而是学生“怕麻烦”不愿意“画图”,甚至是学生“看不懂”题目要求,尤其是一些“人为约定”的直观图示。用类似的测评任务得不到真实的评价效果。

