主动负荷参与的含高比例分布式光伏台区经济自治运行

李铁成，杨少波，傅本栋，范辉，罗蓬，吴赋章，王弘利，杨军，李顺，胡雪凯

(1.国网河北省电力有限公司电力科学研究院，石家庄050021；2.武汉大学电气与自动化学院，武汉430072；3.国网河北省电力有限公司，石家庄050021)

0 引言

“双碳”背景下，未来的新型电力系统具有该比例的新能源接入和大量的柔性负荷参与这两个显著的特征[1-3]。然而，新能源的出力具有很大的随机和波动性，难以确定，另一方面，柔性负荷的用电无法精准预测，受用户行为干扰[4-6]。在此背景下，合理地协调台区的分布式光伏资源，促进光伏的消纳，同时优化台区主动负荷的运行调度，对于台区的经济自治运行具有很大的应用价值，对于需求侧管理模式的推广发展和电力资源优化配置都有十分重大的现实意义[7]。

国内外学者对分布式新能源的消纳已做了大量研究，大致可分为两部分：源侧消纳[8]和荷侧消纳。在源侧消纳上，文献[9]利用储能系统的可用容量管理技术，实现屋顶太阳能光伏消纳；文献[10]利用多能互补方式，提出多时间尺度能量协调优化方法。在荷侧消纳上，文献[11-12]有效整合了需求侧响应的资源，实现了电能的虚拟化存储。然而，由于较大的投资成本和较高的运维复杂度，源侧消纳并不适用于分布式光伏台区对光伏的消纳要求[13]，故而广泛采用荷侧消纳。

随着信息科学与技术的发展，智能电网的建设如火如荼，各种智能家居层出不穷，由于其精准的信号采集能力和先进的通信控制技术，智能家居负荷能够根据电力系统的需求作为可以调控的负荷参与电网运行[14]。文献[15]提出一种高效的方式整合分布式可再生能源、储能设备及主动负荷，提出负荷平移求解策略。文献[16]根据负荷的强关联性和时间关联性，完成主动负荷中可平移负荷的辨识，为提高用户参与需求响应的积极性提供数据基础。文献[17]根据冷热电联产(combined cooling heating and power，CCHP)系统有功负荷的特点，从供需双方匹配需求和热电比的角度，建立了有功负荷转换模型。最后，通过仿真验证了主动负荷转移在CCHP系统调峰填谷和降低成本中的作用。然而，上述文献集中于将主动型负载的可调功率视为确定的，实际中，海量柔性负荷具有很强的不确定性特征，含高比例分布式光伏台区的主动负荷与分布式光伏协同优化运行是双重不确定性环境下复杂度极高的优化问题[18]。

目前，针对不确定性优化问题，一般可采用随机规划[19]和鲁棒优化[20]两种解决方案。其中，随机规划具有明显的局限性，难以准确获取实际工况下不确定变量的分布，不符合随机规划对不确定变量概率分布特征的精度要求。鲁棒优化不需要获得不确定变量的分布特征，只需要用不确定集来描述，优化目标可以保证获得不确定集上任意一点的鲁棒最优解。

为实现双重高不确定性条件下的台区经济自治运行，促进“源-网-荷”协调，本文首先考虑主动负荷的灵活可调节性和需求响应特性，以运行成本最低为目标建立台区经济自治运行确定性优化模型；接着，计及高比例光伏和海量柔性负荷双重不确定性，通过鲁棒多面体不确定集合在时间、空间、功率区间3个方面构造表征源侧和荷侧不确定特征，以此构建计及源荷双重高不确定性的台区经济自治运行不确定性优化模型；随后通过鲁棒对等将其转换为可解耦迭代求解的鲁棒优化模型，采用ADMM算法实现了模型的分布式迭代求解。

1 用户需求响应特性下主动负荷类型划分

家用电设备按照功率是否可变来划分可以分为恒功率设备和可变功率设备，根据运行特性又可分为可中断负荷和可平移负荷。如照明设备，其用电时间相对固定，负荷波动不大，既无储能特性，也没有负荷转移调控的空间，称为固定负荷；如电饭煲、洗碗机等，其用电时间相对灵活，可在一定范围内转移，此类用电负荷称为可平移负荷；如热水器、空调、取暖器等，其用电时间段内可随时中断，中断后其工作状态发生变化，从而导致耗电量减小，此类用电负荷称为可中断负荷。可平移性负荷和可中断性负荷都属于灵活负荷。3种主动负荷的分类和典型例子如表1所示。

表1 主动负荷及其典型示例

用户通过灵活负荷调整实现用电任务的优化，在日用电时间段内(0:00—24:00)，对一天时长进行h等分，并对时段依次编号为1～h。设H为用户用电任务调度的时段集合，即H={1, 2, 3,…,h-1,h},|H|=h；设t为时段变量，t∈H；设S为在H上运行的所有用电任务集合，S={task1, task2,…, taskN}，|S|=N，N为用电任务总量；i为用电任务变量，i∈S。假设Pi为任务i的运行功率向量，有Pi={pi,1,pi,2,…,pi,t,…,pi,h}，pi,t为任务i在t时段上的功率。因此第j个用户Xj在t时段上的负荷功率为：

(1)

2 台区经济自治运行的确定性优化模型

分布式光伏台区一方面接受上层配电网运营商的统一调度，另一方面为了使台区内部的整体效益最大化，需要考虑主动负荷和分布式电源的不同特性，优化引导内部各个主体的功率分配，实现经济自治运行，其在实际情况中对应为台区管理者或台区智能终端。因此，如何根据不同可调节的主动负荷的行为特性和可调度潜力来使目标尽可能最优，是分布式光伏台区经济运行的主要问题所在。

本文假设分布式光伏台区中存在其他类型的分布式电源，且忽略光伏电站的其他运营维护成本，仅考虑建设成本，则整个分布式光伏台区的总经济成本包括主动负荷的调度补偿成本、分布式光伏台区与配电网的功率交互成本及其他分布式电源的燃料和启停成本，其中，功率交互成本间接反映了光伏的消纳水平，而由于光伏发电的启停成本和燃料成本几乎为0，其他分布式电源的燃料和启停成本的存在也反过来促进了光伏消纳。以最小化总成本为目标，构造以下目标函数：

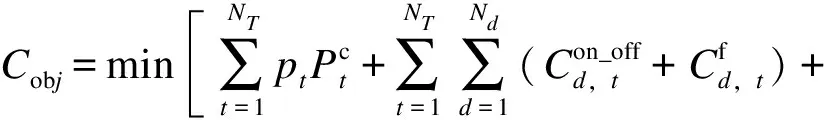
(2)

(3)

式中：ad、bd、cd为成本系数；Pf,d,t为在t时段第d个分布式电源的总出力。

台区中的主动负荷有可平移和中断特性，台区内第j个用户Xj在t时段的主动负荷调度补偿成本CXj,t根据用户主动负荷的调节或削减情况决定。由第1节所述主动负荷特性可知，固定负荷并不具备灵活调节特性，则无调度补偿成本，因此，用户Xj在t时段的主动负荷调度补偿成本CXj,t只与主动负荷有关。对于用户Xj来说，其t时段的灵活负荷总功率为：

(4)

(5)

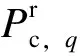
则第j个用户Xj在t时段的主动负荷调度补偿成本CXj,t为：

(6)

式中αt为t时段的调度补偿价格。

考虑如下约束条件。

1)其他分布式电源运行时存在以下对∀k,t均成立的约束条件。

(7)

2)台区功率平衡约束条件为：

(8)

其中：

(9)

(10)

3 分布式光伏台区鲁棒优化调度模型

鲁棒优化在求解之前不用提前给出变量的概率分布情况，其变量的波动范围采用不确定性集合，保证在最恶劣列的极限情况下的解都具有良好的结果[21-23]。由于考虑最恶劣情况下的优化，其保守性较强[24]。自适应鲁棒优化基于随机变量的实际变化进行策略调整，近年来在电力领域的优化运行问题中有较好效果[25]。

不确定集的不同选择会产生完全不同的优化结果，目前最为常用的不确定性集合包括盒式不确定集、椭球不确定集和多面体不确定集[26]。其中，盒式不确定集形式最为简洁清晰，也叫区间集。由于鲁棒优化是一种考虑最坏情况的优化方法，使用区间集进行优化一般都会在区间的上下限上进行计算。但是在实际中，这种情况发生的概率极低，因此容易过于保守[27]。椭球不确定性集优点在于可以考虑到随机变量之间的相关情况，更适用于地理位置靠近的新能源的功率特性分析[26]，当求解线性规划、二次优化问题和锥二次优化时可以转化处理，然而对于其他的诸多问题的求解存在限制。椭球不确定集虽然可以在一定程度上体现随机参数之间的相关程度，但问题求解的复杂程度也随之增加，所以没有得到广泛运用。本文采用多面体不确定性集合，虽然多面体集合无法引入随机变量之间的关联性，但其为线性结构、可以根据需求控制不确定度，且相对于盒式不确定集不容易出现过度保守的情况，在实际工程问题中广受青睐。

3.1 分布式光伏多面体不确定性集合

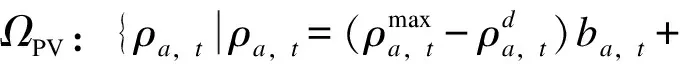
(11)

其中：

(12)

3.2 主动负荷多面体不确定性集合

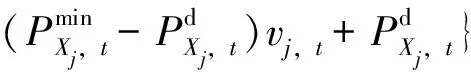
(13)

其中：

(14)

4 基于多面体集合的自适应鲁棒优化模型

第2节建立的分布式光伏台区经济自治运行确定性的优化模型，并未涉及到光伏和主动负荷的双重不确定性，本节利用第3节建立的分布式光伏和主动负荷的多面体不确定性模型，考虑源荷双重高不确定性，构建自适应鲁棒优化模型。由第3节可知，ρa,t和PXj,t的多面体不确定集合ΩPV和ΩQ会使台区功率平衡约束(8)具有随机性，同时会使确定性优化目标函数(2)产生相应变化。对式(8)作一个等效的替代，有：

(15)

(16)

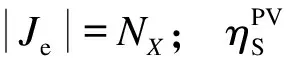
对等变换(15)只研究了某一时间区间内的情况，而目标函数是研究全部时间范围内的成本。类似的，将目标函数进行鲁棒等效变换，得到：

(17)

(18)

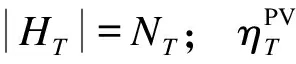
5 自适应鲁棒优化模型的求解

第4节提出的鲁棒优化模型中，决策变量较多，不仅包括各类功率的输出输入，相应的对偶变量和状态变量也需要求解计算。另一方面，每一个分布式光伏台区可能存在大量的分布式光伏和主动负荷资源，使计算的规模和复杂程度变得很大。因此，本文使用ADMM算法来对问题进行转换并求解，其中，每一个包含灵活资源的用户都可以在允许范围内对其拥有的主动型负荷进行单独的优化控制。但是注意到式(17)中存在取值范围为{0，1}的状态变量，导致目标函数不是一个凸函数。文献[27]验证了交替方向乘子算法在解决含0，1变量问题时的有效性，保证了问题的求解。

引入增广拉格朗日乘子，得到式(19)：

(19)

(20)

基于ADMM算法，对式(19)做解耦处理，得到如下迭代计算式：

(21)

(22)

式中：r为迭代次数；λj,t(r)和PXj,t(r)为第r次拉格朗日乘子和负荷功率的计算结果。用户Xj的单独迭代计算式为：

(23)

联立式(7)—(10)和式(12)，可得式(23)的等效形式。

用户根据式(24)单独求解。在NX用户得到优化求解结果后，再根据式(25)计算下一代的PXj,t。

(24)

(25)

λj,t的迭代更新算式为:

(26)

式(21)、(24)—(26)即为式(19)的分布式迭代计算方程。式(27)为终止条件，θ为常数。

(27)

根据以上的计算求解式和分析过程，可以总结出分布式光伏台区自适应经济鲁棒优化的总体流程，即：

1)确定时间范围T和步长Δt，根据不同类型主动负荷的历史信息和预测结果，根据用户的最低负荷需求(固定负荷)得到PXj,t迭代的初始值；

2)设定参数ρ，λ和θ，r=1；

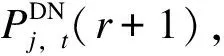
4)将结果代入式(27)，判断迭代终止与否。小于等于收敛间隙，则直接进入步骤 6)，结束计算。若大于收敛间隙，则依据式(26)计算新的λj,t(r)；

5)r=r+1，退回至步骤 3)进行新一轮的迭代计算；

6)计算终止。

6 算例分析

6.1 参数设置

图1 基础负荷与市场电价

6.2 鲁棒优化结果分析

本文选择ρ为160，7次迭代计算后，计算终止，优化结果收敛到最优值。T时段内光伏电站的历史预测功率如图2所示。

图2 光伏电站预测功率

光伏电站预测功率如下。

台区与配网的交互功率和其他分布式电源功率以及主动负荷的总功率优化结果如图3所示。光伏电站预测功率鲁棒成本优化结果如图4所示。

图3 鲁棒功率优化结果

图4 光伏电站预测功率鲁棒成本优化结果

图3中光伏的功率曲线是在鲁棒控制系数控制下考虑其功率波动后的出力曲线。交互功率成本的高低受市场电价影响，在0:00—06：00时段，由于市场电价较低，交互功率成本小于系统内其他分布式电源的发电成本，因而此时段内交互功率较高，系统内其他分布式电源则处于停机状态。在其他时段为了使系统的运行成本最小化，其他分布式电源以最优的发电功率补偿电力需求，交互功率下降。

基于图3、图4的分析，18:00—22:00期间，互动电量不高，但市场电价高导致该时段主动负荷产生电力需求，互动电量成本仍然较高。从图4可以看出，有功负荷调度所需要的调度补偿成本在电价高峰期较高，在电价低谷期较低。这是因为电价高的时期也是基础负荷的高峰期，用户会通过调节转移负荷和可中断负荷来降低电量，调度的补偿成本增加。然而再低谷期时两类负荷接近固定负荷，调度补偿成本较小。因此，本文提出的模型和求解方法能够使用户利益最大化，减少成本的支出。

6.3 分布式与集中式优化对比分析

在不考虑主动负荷灵活调节差异性时，将3类负荷均视为可中断负荷，不采用分布式的求解方法，优化结果如图5所示。

图5 分布式与集中式优化对比

由图5可知，分布式优化相比于集中式，更能显著减低台区总成本。表2给出了分布式与集中式的求解效率和弃光率的对比结果，分布式相比于集中式求解效率更高，且更能消纳光伏。

表2 求解效率与弃光率对比

6.4 考虑双重不确定性与单侧不确定性的优化结果对比

仅考虑源侧即光伏侧的不确定性，其与本文所述双重不确定性的优化对比结果如图6所示。由图6可知，本文所述双重不确定性优化方法，更能显著减低台区总成本；表3给出了两种方案的求解效率和弃光率的对比结果，考虑双重不确定性并未显著提高求解效率，但大大提高了光伏消纳。

图6 双重不确定性与单侧不确定性优化对比

表3 求解效率与弃光率对比

7 结论

本文针对新型电力系统中高比例分布式光伏和海量灵活资源接入使得系统经济安全运行受到巨大挑战的问题，提出了一种计及源荷双重高不确定的“源-网-荷”协调分布式光伏台区经济自治运行方法。通过在台区经济自治运行确定性优化模型的基础上构建表征源荷波动的时间、空间、功率区间鲁棒多面体不确定集合，构建了台区经济自治运行不确定性优化模型，采用鲁棒对等将不确定性优化模型转换为可解耦迭代求解的鲁棒优化模型，并利用ADMM算法完成了模型的分布式迭代快速求解，实现了“源-网-荷”协调互动。仿真分析与对比实验证明了本文所提模型和方法的可行性、合理性和优势，将为新型电力系统的建设和运行提供指导。具体结论如下。

1)计及源荷双重高不确定性的台区经济运行的分布式优化方法在求解效率上更优于集中式优化方法，且优化结果能更好地降低台区运行成本。

2)通过考虑源荷侧双重高不确定性，协调“源-网-荷”运行，能够降低用户用电成本的同时促进分布式光伏消纳。

3)相较于仅考虑单侧不确定的场景，本文所提的考虑源荷侧双侧不确定性算法，不仅能够保证求解效率，还能减小弃光率，从而减小运行的总成本。