风洞模型主动减振结构作动器效率定量表征与提升研究

曾开春， 欧阳炎,2， 寇西平,2， 余 立， 杨兴华

(1.中国空气动力研究与发展中心 高速空气动力研究所，四川 绵阳 621000； 2.西北工业大学 航空学院，西安 710072)

在跨声速风洞试验中，支撑系统容易对飞行器风洞试验模型(简称风洞模型)表面的流场产生显著干扰。为了尽可能降低支撑干扰，支杆通常设计得非常细长，导致风洞模型支撑结构存在频率低、阻尼小的振动模态，在气流激励下容易产生大幅度振动问题[1-2]。风洞模型剧烈振动，不仅影响试验数据的精准度，还会威胁风洞安全[3-6]，致使试验包线严重受限。解决跨声速风洞模型振动问题的重要手段是发展振动控制能力强，且作动器能集成到支撑结构内部的风洞模型减振系统。

国外自20世纪60年代就开始基于被动吸振器发展风洞模型减振系统[7]，但由于被动吸振器的吸振能力有限，难以对跨声速风洞模型振动实现有效地抑制。随着大推力压电陶瓷作动器技术的逐渐成熟，国内外风洞试验部门开始探索适用于高速风洞的模型主动减振方法。主要方案是在支杆内部嵌入压电陶瓷叠堆作动器(简称压电作动器)，构成风洞模型支撑/振动控制一体化结构，通过主动控制技术实现风洞模型振动抑制。然而，由于压电作动器虽然推力大，但行程仅为微米量级，若安装压电作动器的结构设计不合理，将导致主动减振系统难以达到理想的减振效果。因此，主动减振结构设计成为风洞模型主动减振系统研制中的一个核心关键问题。

Balakrishna等[8]以Pathfinder-Ⅰ飞机风洞模型尾支撑结构为对象，研制了一套风洞模型主动减振装置。该装置在支杆前端嵌入4个压电作动器用来抑制风洞模型的纵向(垂直方向)和横向(水平方向)振动。试验结果表明该减振结构可以减小风洞模型振动幅度、拓展试验迎角范围，但在大迎角分离气流形成强烈激励时，风洞模型仍会出现大幅度振动。为了提高减振系统的减振能力，Balakrishna等[9-10]又在对风洞模型支撑结构动力学理论分析基础上，研究了能够提高作动器效率的压电作动器布置方式。

欧洲在ETW(European Transonic Windtunnel)风洞中也研制了一套位于支杆前端的主动减振结构[11-12]。14个小型压电作动器呈环状布置在减振结构中，并通过14个预紧螺栓固定在支杆与天平之间。该结构能够抑制风洞模型在纵向、横向和轴向的振动，但是由于压电作动器能力有限，其在振动最严重的风洞模型纵向上，控制效果还难以满足使用需求。为此，ETW又在支杆后端研制了一套纵向减振结构[13-14]，以提升对风洞模型纵向振动的抑制能力，但是ETW并未公布该后端主动减振结构的技术细节。

近年来，国内高校和相关研究机构也开展了风洞模型振动主动控制研究。陈卫东等[15-16]使用置于模型内的电磁式作动器来对风洞模型振动进行主动抑制。Liu等[17-18]基于压电作动器发展了一套位于支杆根部的风洞模型主动减振结构。该结构通过预紧装置将压电作动器嵌入支杆根部，并将沿周向分布的4个压电作动器划分为上、下两组，通过其差动作动来抑制风洞模型纵向振动。

为解决主动减振系统在跨声速分离流激励下出现的减振能力不足问题，余立等[19-21]提出在主动减振结构中引入两个弹性铰链(简称铰链)来削弱结构对压电作动器的约束刚度，进而达到增加压电作动器效率、提升主动减振结构减振能力的目的。然而，在该主动减振结构的铰链设计中，由于需要考虑的设计参数多、约束条件多，而且各参数之间交互耦合，给该类结构的设计带来很大困难[22]。因此，探索铰链参数对主动减振结构作动器效率的影响规律，摸清作动器效率的敏感性特征，可以为风洞模型主动减振结构的方案设计和性能提升提供参考。

本文针对某运输机标模风洞试验尾支撑主动减振结构，结合模态试验和有限元模态分析，建立能表征纵向关键振动模态的动力学-控制系统简化模型，探索适用于主动减振结构的作动器效率表征方法，并着重就铰链参数对作动器效率的影响规律及物理机理进行分析，为提高作动器效率和减振结构性能改进提供方向和策略。

1 主动减振结构方案

中国空气动力研究与发展中心针对风洞测力试验模型尾支撑装置，以控制支杆纵向振动模态为目标所发展的双弹性铰链主动减振结构方案，如图1所示。该方案在支杆根部的接头中嵌入压电作动器，形成主动减振结构，并搭建外部控制软、硬件，形成闭环主动减振系统。在风洞模型发生振动时，实时控制器根据应变天平动态信号和减振控制律生成实时控制信号，输出给压电作动器的驱动器，驱动压电作动器产生轴向推力，再经过铰链结构转化为抑制模型纵向振动的控制力矩。

图1 双弹性铰链主动减振系统方案Fig.1 Schematic diagram of active damper with double-hinge structure

主动减振结构的主要设计参数包括两个铰链的几何尺寸、位置参数等。图2给出了铰链设计参数的示意图，给出的参数包括上、下铰链的长度、厚度和铰链中心线偏离支杆轴截面的距离(简称“偏离距离”)。

图2 铰链的设计参数Fig.2 Design variables of flexible hinges

2 主动减振结构作动器效率定量表征

在铰链参数设计及分析中，首先需要解决主动减振系统的作动器效率定量表征问题。本章介绍了几种作动器效率的表征方法。

2.1 绝对可控性表征方法

根据Hamdan[23-24]的系统可控性理论，可以建立起振动主动控制系统某个作动器对结构某阶振动模态的可控性。

基于该理论，压电作动器对某阶模态的可控性可由式(1)获得。

(1)

求解式(1)，需要建立支撑系统状态空间形式的动力学解析模型，获得系统的状态矩阵A和控制矩阵BU。

将式(1)度量主动减振结构作动器效率的方法称为“绝对可控性表征方法”，度量出的作动器效率称为“绝对可控性”。

2.2 相对可控性表征方法

一般控制系统的作动器设计[25]中，作动器不同布局设计并不显著影响系统的固有模态特性。然而，对于风洞模型主动减振结构，在铰链参数改变时，不仅会影响压电作动器的作动效率，同时也会改变支撑结构整体刚度，进而造成系统振动特性的改变。此时，一种可能的情况是：为提升减振能力，更改了铰链设计参数，虽然小幅度提升了压电作动器对模型支撑结构的振动控制能力，但气动力对支撑结构的激励能力却大幅度提升，结果是在相同风洞试验条件下，风洞模型振动幅度不但没能降低，反而增大了。

针对风洞模型主动减振结构这一特征，本文使用压电作动器对结构模态的控制能力与气动力对该模态激振能力之比作为主动减振结构作动器效率的表征，即

(2)

式中，fAi为气动力作为控制输入时，第i阶模态的可控性，同样可根据系统可控性理论获得

(3)

此外，为方便描述和区分，将式(2)度量主动减振结构作动器效率的方法称为“相对可控性表征方法”，度量出的作动器效率称为“相对可控性”。

2.3 静态控制力矩表征方法

根据主动减振结构振动控制原理，压电作动器作动时主要通过在主动减振结构前端产生一个控制力矩来抑制模型的振动。因此，一种工程中常用的，较为粗略的作动器效率表征方法是直接使用该控制力矩的静态最大值(简称“静态控制力矩”)来度量主动减振结构的作动器效率。

为确定静态控制力矩，可给压电作动器输入最大电压，获得风洞模型的静态俯仰角增量θsU。另外，在主动减振结构前端施加一确定力矩M0，获得风洞模型的静态俯仰角增量θs0。此时，用于表征主动减振结构作动器效率的静态控制力矩值为

(4)

3 风洞模型支撑结构动力学建模

为了获得2.1节、2.2节中计算模态可控性所需的振动控制系统状态矩阵和控制矩阵，需要建立解析的动力学/控制耦合模型。由于风洞模型支撑结构拥有无穷阶振动模态，为了确定需要描述的结构振动模态及关键特征，首先根据风洞模型支撑结构在风洞试验过程中的典型响应历程，配合地面模态试验，确定关键模态频率和振型；然后应用有限元法对风洞模型支撑结构进行模态分析，获得这些关键模态中各零部件运动/变形情况；最后，对结构进行适当简化，建立能准确捕捉这些关键模态特性的低阶简化模型。

3.1 风洞模型支撑结构振动特征

从大量风洞模型振动问题的统计情况来看，不同风洞模型的振动呈现出相似特征。为此使用某运输机标模进行风洞试验振动测试。试验中在风洞模型头部布置了加速度传感器，测量风洞试验过程中模型纵向和横向的振动加速度。试验过程中，来流马赫数保持为0.7不变，模型迎角从0°～8°连续变化。

图3给出了在该运输机标模风洞测力试验过程中，测得的加速度时间响应及其功率谱分析结果。试验中，当迎角增大至约7°时，风洞模型纵向振动幅度显著增大。由图3可以看出：振动最显著的模态是频率约8.8 Hz的纵向第一阶模态，功率谱约为24.3 dB；其次是频率约16.9 Hz的纵向第二阶模态，功率谱约为-4.4 dB。因此，本文以较为准确描述这两阶振动模态为目标来建立简化模型。

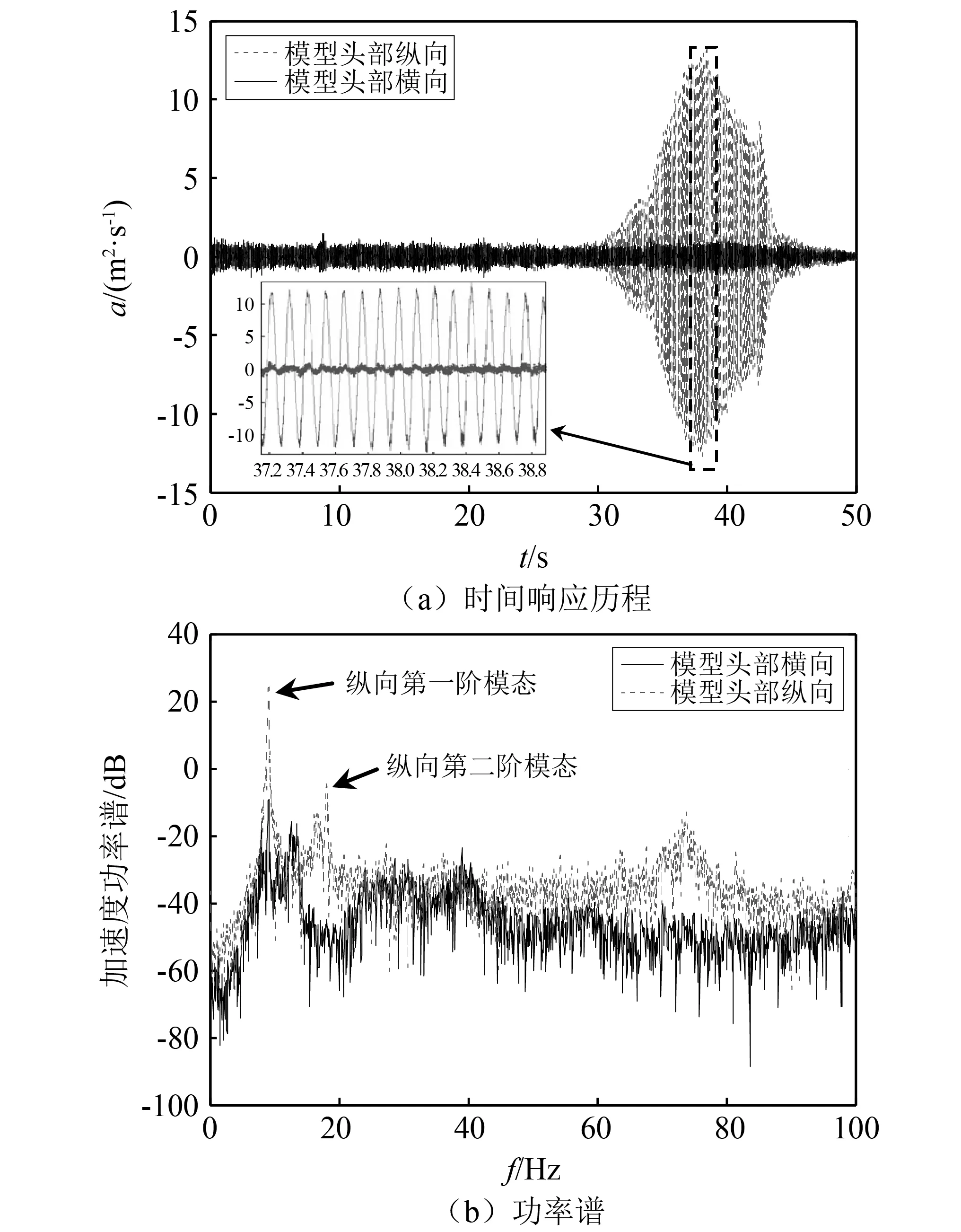
图3 某运输机标模测力试验过程的加速度响应Fig.3 Time history of an aircraft model acceleration during wind tunnel test

在风洞试验前，为了确定功率谱中各频率所对应的结构模态振型，还对支撑结构进行了地面模态试验。图4给出了纵向前两阶模态振型。由图4可以看出：纵向第一阶模态主要表现为模型刚体平动；纵向第二阶模态主要表现为模型刚体俯仰。

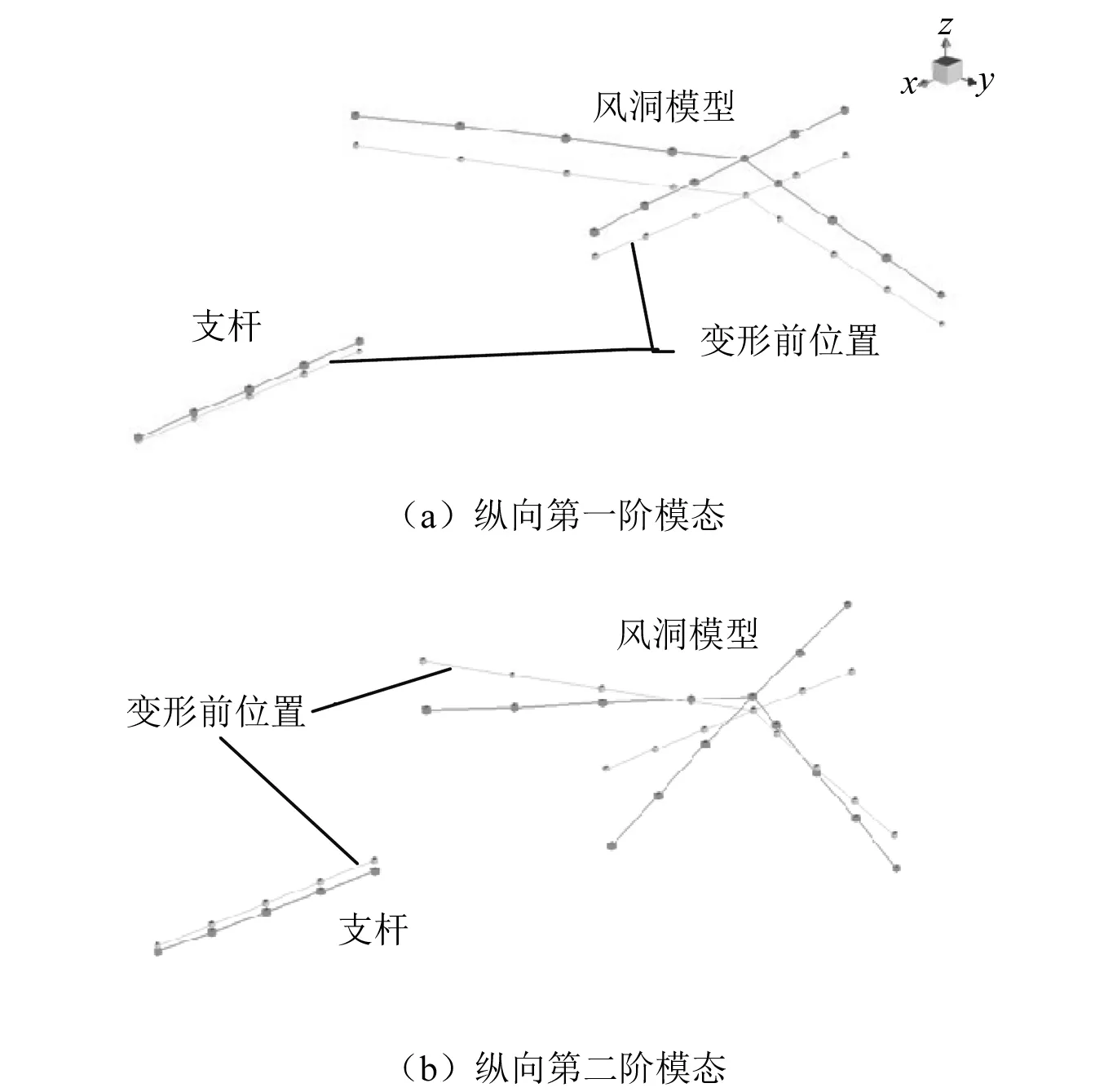
图4 某运输机标模支撑结构模态振型Fig.4 Modal shapes of an aircraft model support mechanism

3.2 有限元分析

根据风洞试验和地面模态试验获得的模型支撑结构关键振动模态总体特征，应用有限元法对支撑结构进行分析，获得这些模态的细节特征，以及压电作动器作动时结构的变形模式。

3.2.1 压电作动器的有限元建模

压电作动器是由经过极化的压电陶瓷薄片叠放、烧结、封装而成。按照第一类压电方程，当施加电场时，在陶瓷片法向(即压电陶瓷片的3-3方向)产生诱导应力，其本构方程可表达为

(5)

式中：σ3和ε3分别为压电陶瓷片在法向的应力和应变；E33为电场为常值时压电陶瓷材料的弹性模量；e33为压电应力常数；t为陶瓷片厚度；U为陶瓷片两端施加的电压。根据式(5)，可得到压电作动器的轴向推力/位移关系为

(6)

式中：ΔlPZT为压电作动器伸长量；LPZT为作动器原始长度；A为作动器承载面积；FA为作动器轴向推力；n为作动器陶瓷片数量。

一般使用的商业有限元软件中没有压电陶瓷分析模块，但有热膨胀分析功能。由于压电作动器的宏观力学特性与热膨胀力学特性类似，因此可以用变温均质材料来近似模拟压电作动器在施加电压时的力学特性。

对于几何形状与压电作动器相同的均质金属，其在受热时轴向受载与轴向伸长量的关系为

(7)

式中：L，A，E分别为该金属的长度、面积、弹性模量；αT为该金属材料轴向线热膨胀系数；ΔT为材料温升。将式(7)变换成式(6)相似的形式，得到

(8)

对比式(8)与式(6)，欲使在温升ΔT的受热金属产生与施加电压U的压电作动器形成相同的力与变形结果，除几何外形、弹性模量相等外，还需满足

(9)

3.2.2 风洞模型支撑结构的有限元建模

有限元建模时需要考虑的结构部件有模型、天平、支杆、减振接头及压电作动器等。由于本文有限元分析的主要目的是进行模态分析，因此忽略了局部细节，例如各零件之间连接螺栓、各种倒角、小走线孔等。

在模态分析中，压电作动器、铰链、支杆、天平等均使用三维实体单元模拟质量特性和刚度特性，而风洞模型由于在关注模态中仅表现为刚体运动，因此采用多个集中质量单元来模拟质量及其分布特性。图5给出了运输机标模支撑结构的有限元模型。

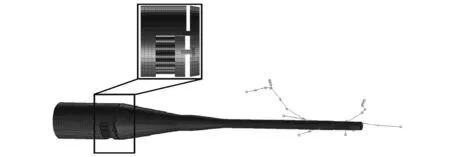
图5 运输机标模尾支撑结构有限元模型Fig.5 Finite element model of the support system for a standard airplane wind tunnel model

图6给出了有限元法获得的纵向第一阶模态和纵向第二阶模态振型。可以看出，有限元分析结果与模态试验结果基本一致。纵向第一阶模态主要表现为模型刚体平动、支杆一阶弯曲弹性振动。该模态主要由支杆的弹性引起，因此将其称为支杆纵向模态。纵向第二阶模态主要表现为模型刚体俯仰，天平弯曲变形，而支杆变形幅度相对较小。该模态主要由天平的弹性引起，因此下文将其称为天平纵向模态。

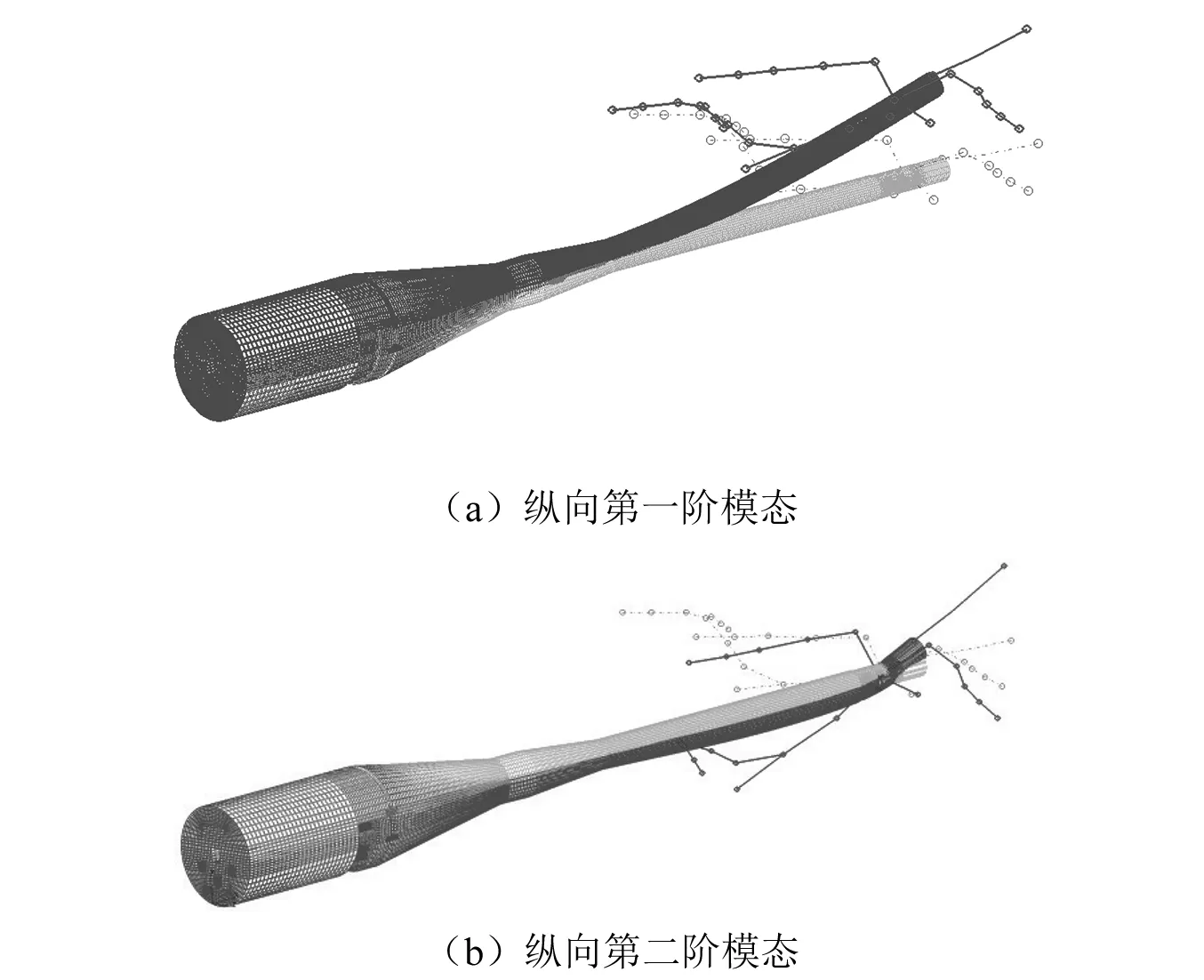
图6 有限元模态分析结果Fig.6 Mode shapes of the support system obtained using finite element method

为了分析压电作动器作动时支撑结构的变形模式，给各压电作动器输入相同的电压，应用有限元法进行静力学计算，结果如图7所示。由图7可以看出，当压电作动器作动时，推动其前方质量块和下弹性铰链向前移动，进而使支杆、模型等都绕上铰链发生转动。在该过程中，两个铰链会发生弯曲和拉压变形。此外，从图7还可以看出，压电作动器作动时风洞模型的运动形式与支杆纵向模态较为一致，因而能够对振动最严重的支杆纵向模态具备较强控制能力，因此以压电作动器对该阶模态的控制能力作为作动器效率设计的主要目标。

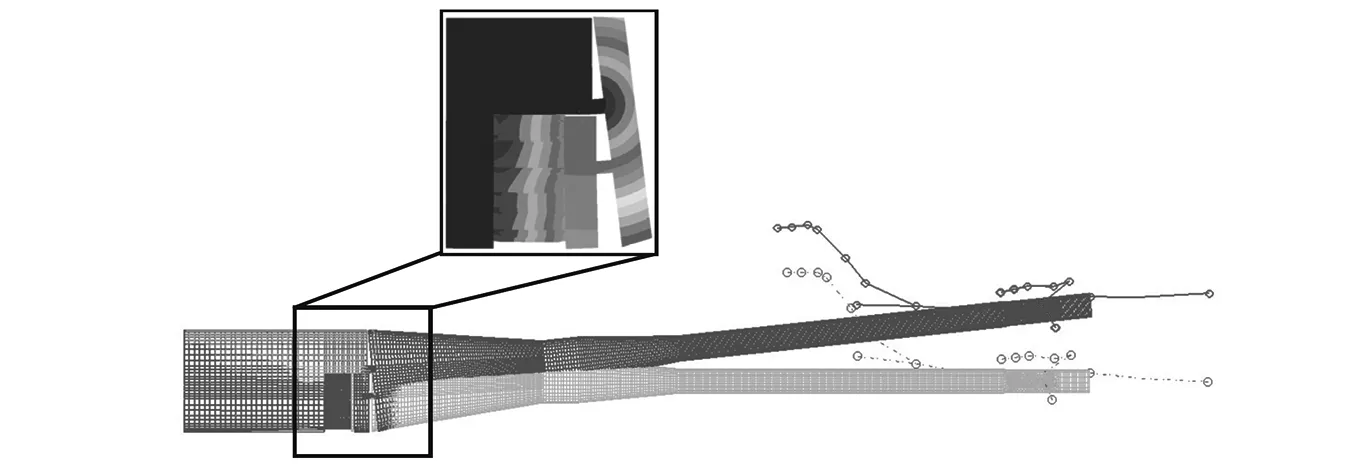
图7 压电作动器作动时支撑结构静变形Fig.7 Static deformation of the support system with piezoelectric stacks actuated

3.2.3 风洞模型支撑结构的简化模型

根据风洞试验及有限元分析结果，对主动减振结构、风洞模型、天平、支杆等进行简化，建立低阶的动力学-控制耦合模型。

如图8所示，简化模型以模拟支撑结构纵向前两阶模态及压电作动器的作动过程为目标，采取的简化主要有：①风洞模型简化为质量为Mm，转动惯量为Jm的刚体；风洞模型质心与天平中心距离为Gm；风洞模型上作用有法向载荷FAy和俯仰力矩Mz，且作用点在风洞模型重心后，与重心距离为GA；②天平简化为刚度为Kb的旋转弹簧；③支杆简化为欧拉伯努利梁；④主动减振结构的两个铰链、压电作动器及预紧螺栓由于对振动模态质量贡献小，均假设为有弹性、无质量、可伸缩变形和弯曲变形的欧拉伯努利梁；与两个铰链及压电作动器连接的结构均假设为无质量的刚性结构；所有压电作动器输入电压保持相位同步，幅值相等(均为U(t))。

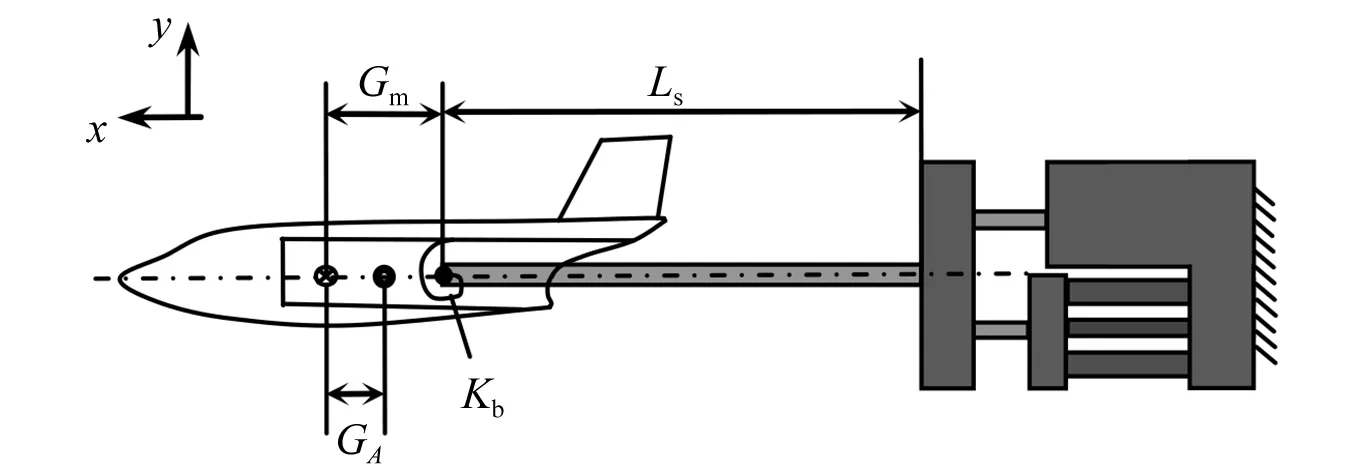
图8 风洞模型支撑结构简化模型示意图Fig.8 Sketch map for the simplified model of the wind tunnel model support system

采用拉格朗日方程，可建立风洞模型主动减振支撑结构在压电作动器作动及气流激励下的动力学模型

(10)

式中：x为动力学系统的状态向量；M，C和K分别为质量矩阵、阻尼矩阵和刚度矩阵；U为压电作动器的输入电压；DU为压电作动器输入电压与等效控制力矩的转换系数矩阵，与压电作动器特性及减振结构设计参数有关；气动力向量FA=[FAy，Mz]′；DA为气动力激励系数矩阵。

根据式(10)，求解其特征方程，获得模态振型，进而得到正交化的模型振型矩阵Φ，再令

x(t)=Φη(t)

(11)

式中：t为时间；η(t)为n×1维的模态坐标向量。将式(11)代入式(10)，经变换后可得

(12)

进一步定义状态向量

可以获得标准形式的控制系统方程

(13)

式(13)中的矩阵A，BU，BA即为求解式(1)、式(3)所需的系统状态矩阵、压电作动器控制矩阵和气动力控制矩阵。

此外，通过式(13)，可以获得风洞模型支撑结构动力学系统特性，以及压电作动器输入电压或气动载荷作用下各部件的动态响应。

4 算例分析

以运输机标模风洞测力支撑结构及其主动减振结构为例，分析压电作动器效率表征方法的适用性，并研究如何通过改变主动减振结构设计参数实现显著提升压电作动器效率。表1给出了主动减振结构设计参数的标称值，并给出了运输机标模测力试验尾支撑结构的材料、几何、物性等参数。

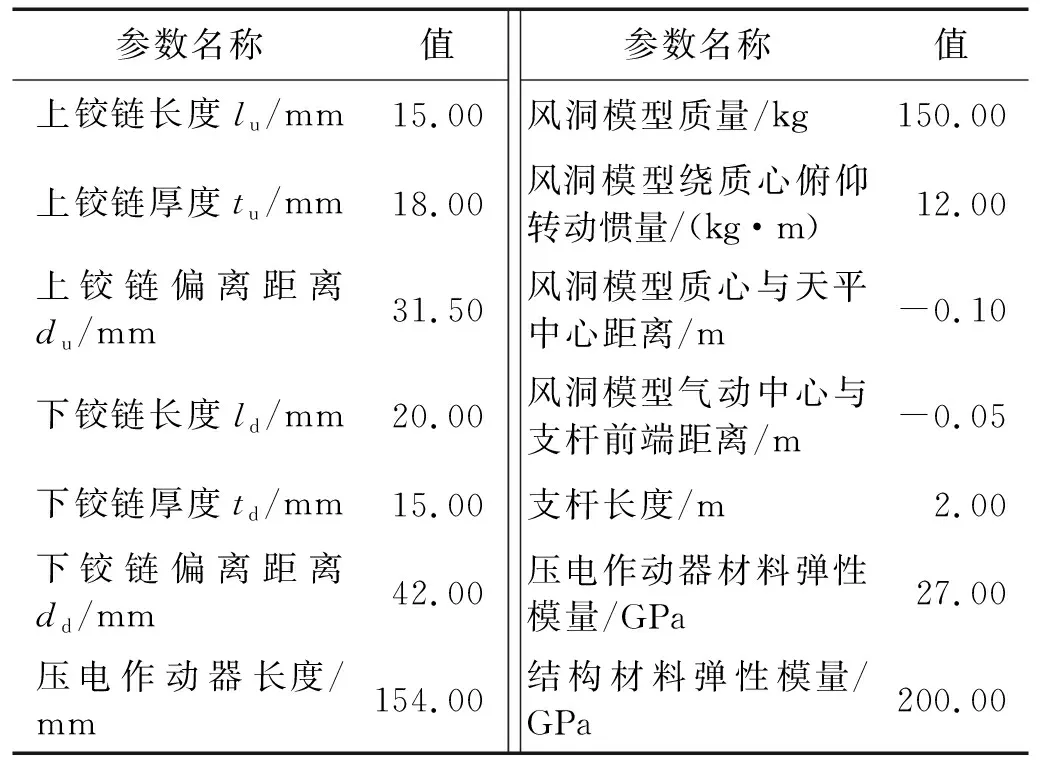
表1 标称减振结构参数

4.1 简化模型验证

通过与试验测试结果和有限元分析结果比较，验证简化模型的有效性。

表2给出了采用4种方法获得的关键模态频率结果及误差，并以模态试验测得的频率为基准计算各方法频率估计误差。由表2可以看出，有限元模型和简化模型对支杆纵向模态和天平纵向模态的频率估计误差均在5%以内。

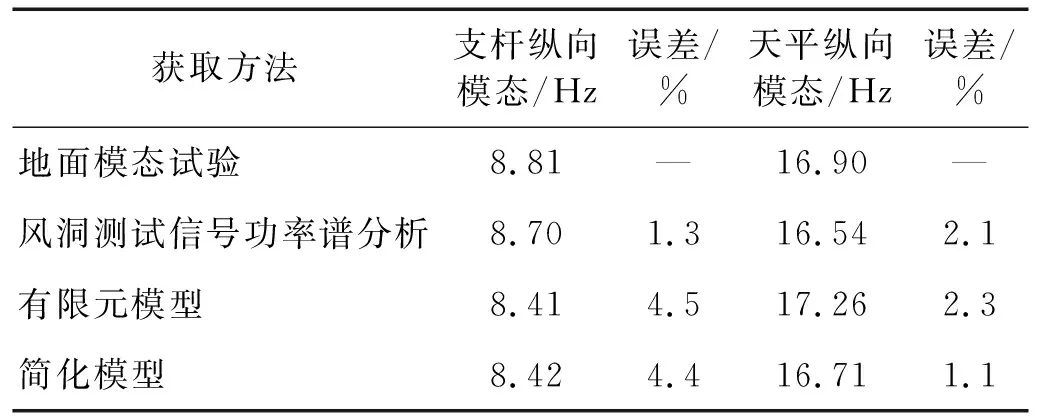
表2 运输机标模尾支撑结构模态频率预测结果

为验证模态振型的相似性，引入模态置信度

(14)

式中：Φm为模态试验获得的振型向量；Φ为其他方法获得的振型向量。式(14)中的CMAC越接近1，说明两个振型越相似。表3给出了有限元模型、简化模型的置信度。可以看出，有限元模型、简化模型获得的模态振型与模态试验测得振型相似度均在0.9以上，说明两种模型均能较准确地捕捉支撑结构关键模态特征。

表3 支撑结构模态置信度

此外，依据图5中压电作动器作动时结构静变形模式，通过对比压电作动器输入电压与风洞模型俯仰角曲线差异，检验压电作动器模型的有效性。分别使用试验测试、有限元分析和简化模型，获得了风洞模型俯仰角随压电作动器输入电压的变化曲线，如图9所示。由图9可以看出，有限元模型和简化模型与测试结果基本一致，表明均能较好地描述压电作动器的作动过程和作动效果。

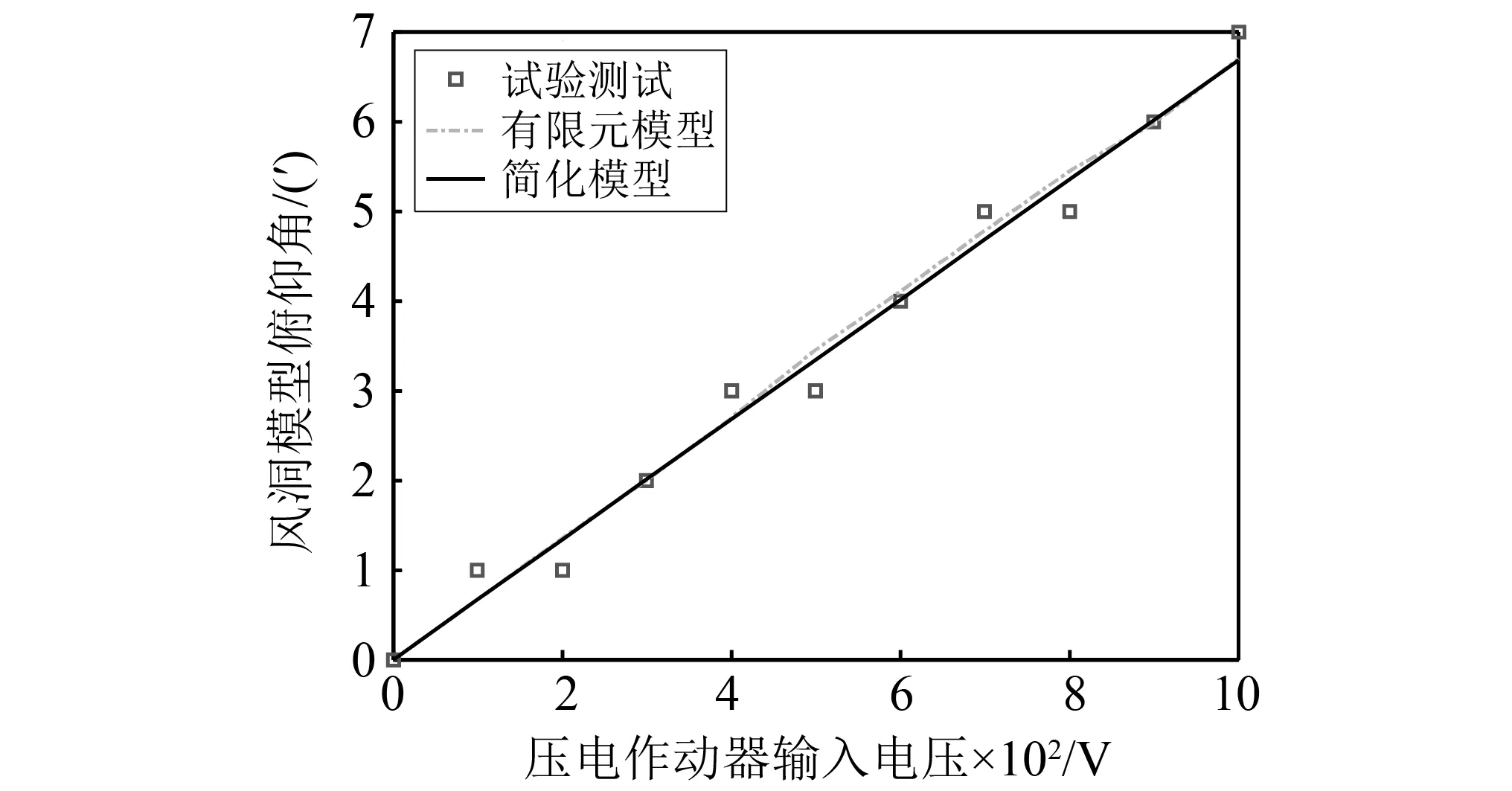
图9 风洞模型俯仰角随压电作动器输入电压的变化Fig.9 Pitch angle of airplane model obtained by different methods

4.2 不同作动器效率表征方法对比

以上铰链偏离距离为例对比3种作动器效率表征方法的特点及适用性。

在上铰链偏离距离改变时，3种方法获得的作动器效率量化结果，如图10所示。图10中对绝对可控性表征方法和静态控制力矩表征方法的结果均进行了尺度放大处理，以使3种方法结果在数值上具有相同量级，便于直观观察。可以看出：3种表征方法均能捕捉到上铰链偏离距离增大过程中，作动器效率先增大后减小这一特征，但3种方法作动器效率极大值对应的上铰链偏离距离值却存在一定差异，依次为静态控制力矩表征方法<绝对可控性表征方法<相对可控性表征方法。

图10 不同作动器效率表征方法对比Fig.10 Comparison of different quantification methods for actuator effectiveness

为了分析绝对可控性表征方法与相对可控性表征方法差异产生的原因，图11给出了气动力对支撑结构模态激励能力变化情况(计算方法见式(5))。可以看出，当上铰链偏离距离设计值小于40 mm时，随着上铰链偏离距离的继续减小，气动激励能力将快速增大，表明此时主动减振结构已经显著地改变了风洞模型支撑系统的支撑刚度。这种情况下，相对可控性表征方法能够更加准确地反映主动减振结构改变后，压电作动器与气流激励力对支撑系统振动控制能力的变化，因而更符合风洞模型主动减振结构的设计需求。

图11 气动激励能力变化Fig.11 Variation of the aerodynamic force excitation capacity

为了方便描述，直接将相对可控性表征方法获得的支杆纵向模态可控性度量称为主动减振结构的“作动器效率”。

4.3 铰链几何参数对作动器效率影响分析

在表1的标称参数基础上，分别改变上铰链和下铰链的厚度、长度以及偏离距离，分析对作动器效率的影响。

4.3.1 铰链偏离距离

图12是上、下铰链偏离距离对主动减振结构作动器效率的影响。结果表明：上、下铰链偏离距离分别增大时，作动器效率均是先增大到极大值后，又开始减小。作动器效率极大值对应的上、下铰链偏离距离分别约为32 mm，42 mm。在极大值附近，作动器效率对下铰链偏离距离变化更为敏感，但当大于80 mm以后，作动器效率对上、下铰链偏离距离的敏感性趋于相同(即图中两条曲线斜率基本相同)。

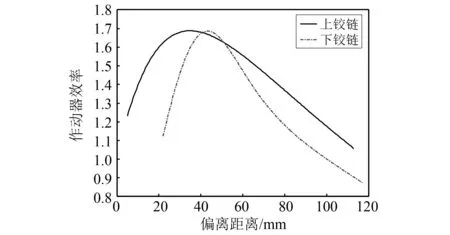
图12 铰链偏离距离对作动器效率的影响Fig.12 Effect of the flexible hinge offset on active damper capability

结合图7的有限元分析结果发现，压电作动器作动时，将推动支杆根部绕上铰链旋转，作用原理类似于杠杆结构。上、下铰链偏离距离之和即为作动器输出力的杠杆力臂，因此，上、下铰链偏离距离之和越大，杠杆力臂越长，铰链结构对压电作动器的约束作用越弱，压电作动器就越容易推动支杆作旋转运动。但由于作动器行程较小，当力臂增大时，能够推动支杆旋转的角度又会减小。以上两个因素共同作用下，便形成了铰链偏离距离增大时，作动器效率先增大又减小的规律特征。

4.3.2 铰链厚度

图13是铰链厚度对主动减振结构作动器效率的影响规律。结果表明上、下铰链厚度对作动器效率影响规律相似，即在12 mm左右具有最大值。当铰链厚度小于12 mm时，随着铰链厚度的增大，作动器效率快速提升，但提升速度随铰链厚度的增加逐渐减小；当铰链厚度大于12 mm时，随着铰链厚度的增大，作动器效率开始降低，降低速率先增大再逐渐减小并最终趋于零。

图13 铰链厚度对作动器效率的影响Fig.13 Effect of the flexible hinge thickness on active damper capability

此外，还可以看出，当铰链厚度小于12 mm时，作动器效率对上下铰链厚度的敏感性接近，但在铰链厚度大于12 mm时，对上铰链厚度的敏感性要远大于下铰链。

4.3.3 铰链长度

图14是上、下铰链长度对作动器效率的影响。结果表明，在上、下铰链长度变化时，作动器效率均存在最大值。在主动减振结构标称设计下，作动器效率取极大值的上、下铰链长度分别约为18 mm，15 mm；当铰链长度超过20 mm时，上、下弹性铰链对作动器效率的影响呈近似线性；作动器效率对两个铰链长度的敏感性变化规律相似，但对下铰链长度敏感性比上铰链略大。

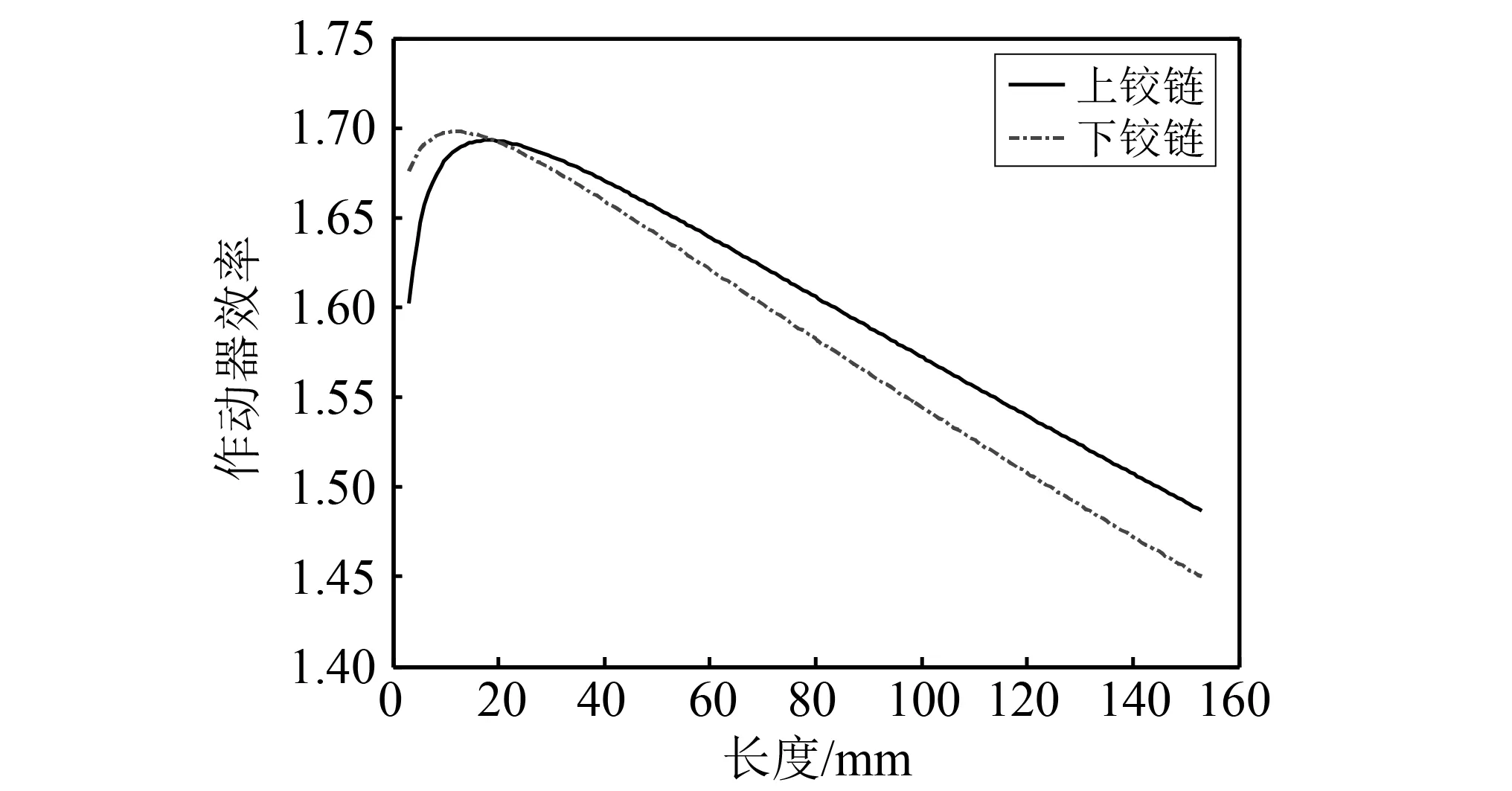
图14 铰链长度对作动器效率的影响Fig.14 Effect of the flexible hinge length on active damper capability

4.4 铰链刚度对作动器效率影响分析

铰链几何参数(铰链厚度、长度等)对主动减振结构作动器效率的影响，不仅非单调还存在严重相互耦合。因此设计人员在主动减振结构的设计和改进时，很难简单地通过增大或减小这些参数来实现作动器效率的提升。为了解决该问题，本节根据压电作动器作动原理，构建出与作动器效率呈单调变化的变量。

分析主动减振结构变形模式，可以发现影响作动器效率的关键因素为压电作动器两端结构的约束刚度。由于铰链的拉伸刚度和弯曲刚度决定了减振结构对压电作动器约束刚度，以下着重分析其对作动器效率的影响规律。

以主动减振结构标称参数为基础获得上、下铰链拉伸刚度和弯曲刚度标称值，并分别改变其中一个值，分析主动减振结构作动器效率的变化情况。仿真结果如图15所示。图15中纵坐标为某个铰链刚度当前值与标称值之比，取值为1表示为标称值。结果表明：与4.3节中铰链几何参数不同，上、下铰链的弯曲刚度和拉伸刚度等对作动器效率影响均为单调；上、下铰链弯曲刚度增大时，作动器效率均线性减小，且作动器效率对上铰链弯曲刚度的敏感性要大于下铰链；作动器效率随铰链拉伸刚度增大呈单调递增趋势，当拉伸刚度倍数值小于0.5时曲线斜率较大，而当大于0.5时曲线斜率快速减小，即当拉伸刚度较大时，作动器效率对拉伸刚度的敏感性将显著降低。

从图15不难得出，铰链弯曲刚度是减振结构影响压电作动器输出的主要因素。压电作动器作动时需要首先克服由其决定的结构弹性恢复力，剩余推力才能推动铰链前方的支杆和模型运动。因此，提升压电作动器对风洞模型振动的控制能力，需尽可能减小铰链的弯曲刚度。与铰链弯曲刚度不同，铰链拉伸刚度决定的铰链伸缩弹性恢复力并不约束压电作动器输出，相反，当铰链拉伸刚度较低时，铰链会在压电作动器输出力作用下产生与压电作动器同量级的伸缩变形，进而造成压电作动器行程损失。

图15 铰链刚度对作动器效率的影响Fig.15 Effect of the flexible hinge stiffness on active damper capability

综上可以得出：降低弯曲刚度是引入铰链结构来提高主动减振结构作动器效率的主要途径，而附带引起的铰链拉压刚度降低则是需要尽力克服的“副作用”。

对于矩形截面铰链，弯曲刚度和拉伸刚度表达式分别为

(15)

式中：KB为铰链的弯曲刚度；KS为铰链的拉伸刚度；w为铰链宽度；l为铰链长度；t′为铰链厚度；E为铰链材料弹性模量。观察式(15)容易看出，可以通过增大w/l，同时减小铰链厚度t′来提升作动器效率。图16分别给出了当上、下铰链以w/l和t′为变量时，主动减振结构作动器效率的等值线图。图16中还给出了0.5倍标称拉伸刚度曲线，该曲线将等值线分成左右两个区域，分别为拉伸刚度高敏感区和低敏感区，并且在低敏感区域内，作动器效率对t′的敏感性要远大于w/l。在主动减振结构设计时，应在右侧的拉伸刚度低敏感区内时选取设计参数，并且当w/l取较大值，t′取较小值时，可以获得作动器效率较高的主动减振结构。

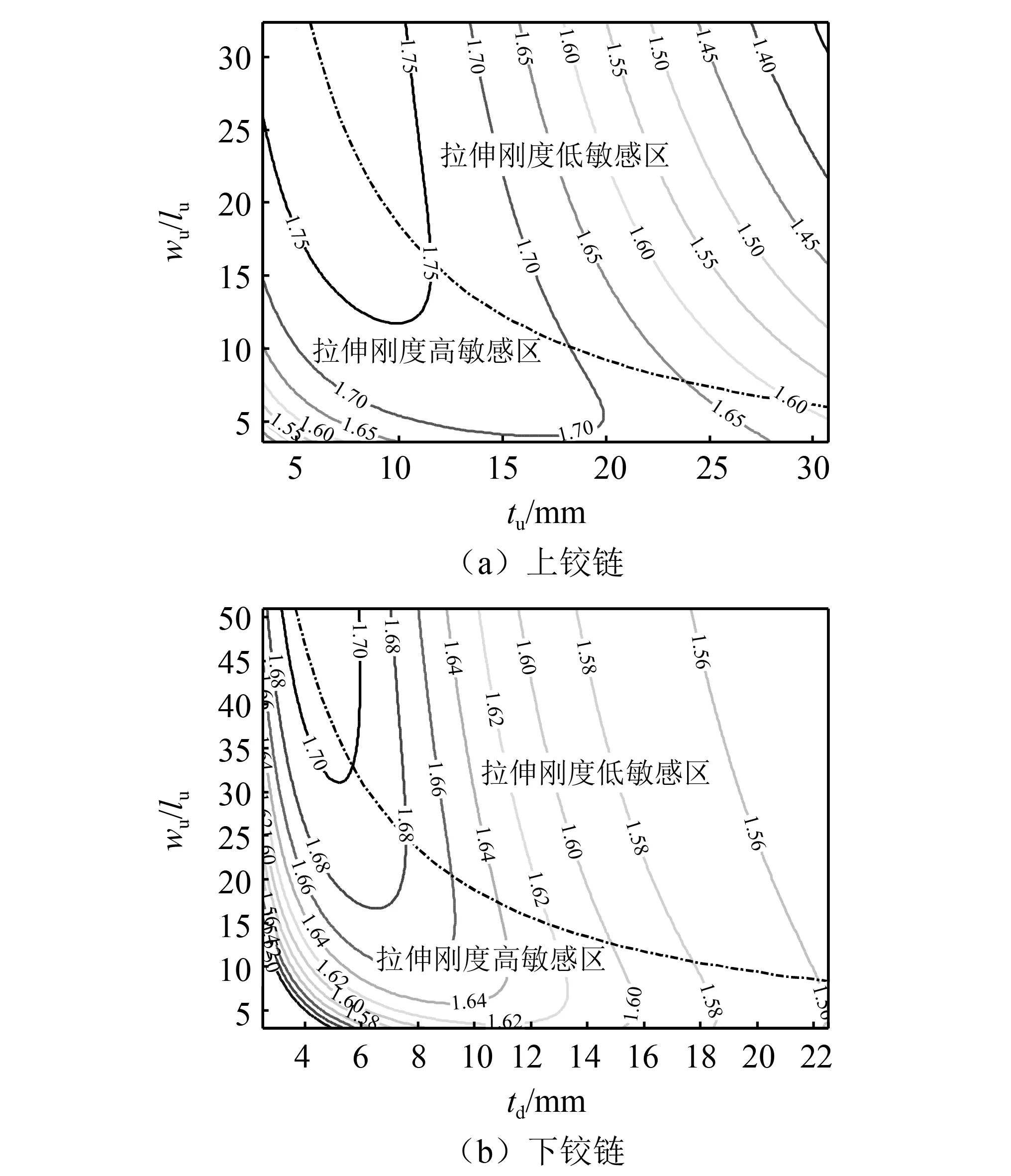
图16 作动器效率等值线图Fig.16 Contour plot of active damper capability

为了验证以上压电作动器效率提升方法，在上、下铰链的拉伸刚度低敏感区内取3个设计点，分别为标称设计点、设计点1和设计点2。3个设计点的铰链参数,如表4所示。设计点1与标称设计点的上铰链宽度和长度均不同，但其比值却保持不变，按照分析结果，其作动器效率将相同；设计点2与标称设计点仅下铰链厚度不同，按照图16结果，其作动器效率将低于标称设计点。

表4 用于验证的3个设计点铰链参数Tab.4 Parameters of flexible hinges in three design cases

将3个设计点的铰链参数分别代入动力学方程式(10)进行时域仿真。其中，压电作动器输入电压幅值均为100 V；激励频率保持与支杆纵向模态频率相同；模态阻尼比均为0.2%。图17给出了3个设计点上，风洞模型质心在铅锤面内的振动位移响应。表5给出了作动器效率预测结果与仿真结果对比。可以看出，标称设计点和设计点1振幅相同，表明这两个设计点的作动器效率相同。而设计点2振幅较前两个设计点低约8.9%，与作动器效率定量描述方法给出的结果一致。以上结果表明本文压电作动器效率提升方法有效。

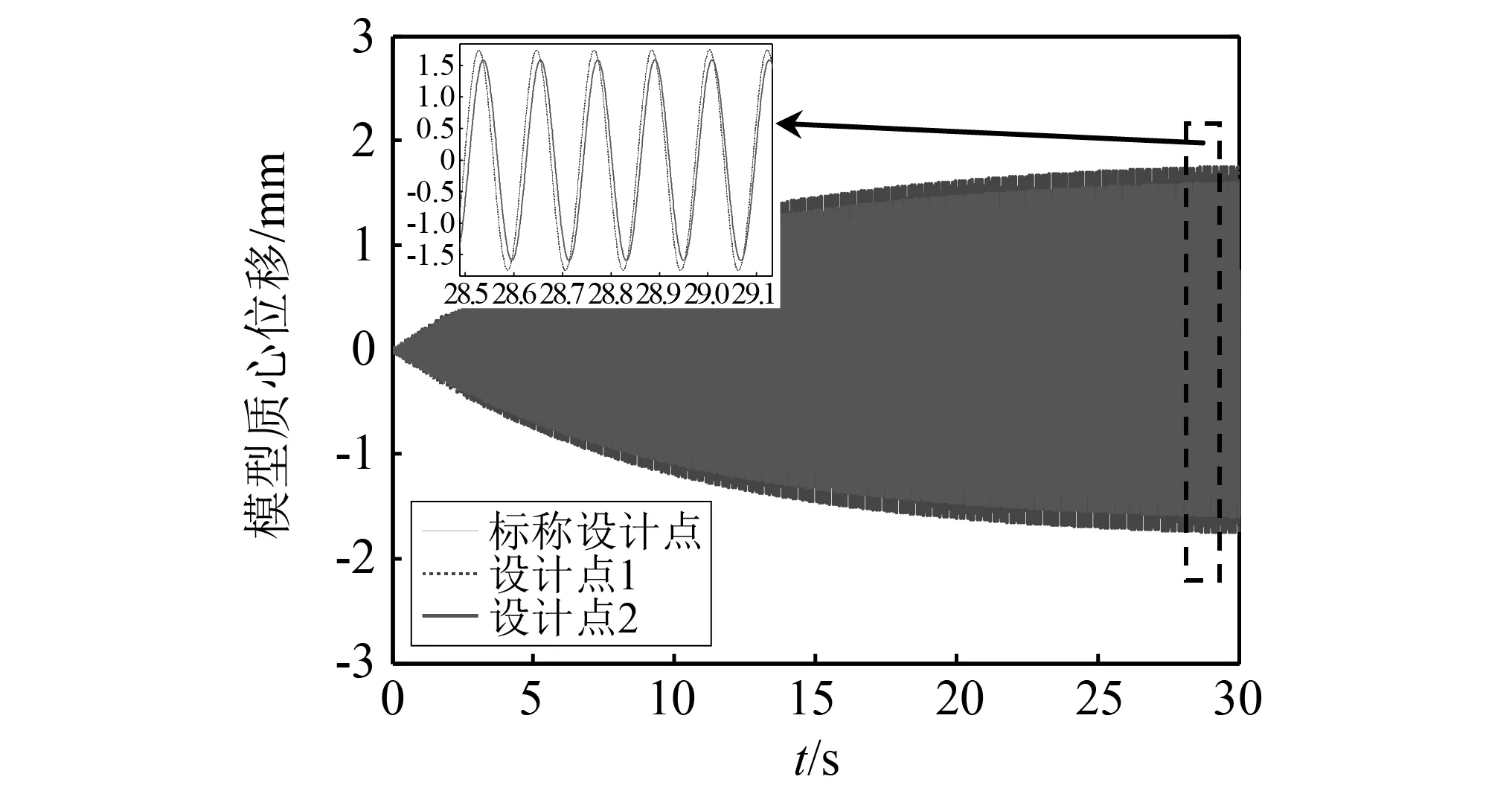
图17 3个设计点结构激励响应对比Fig.17 Comparison of responses of model support mechanism in three design cases

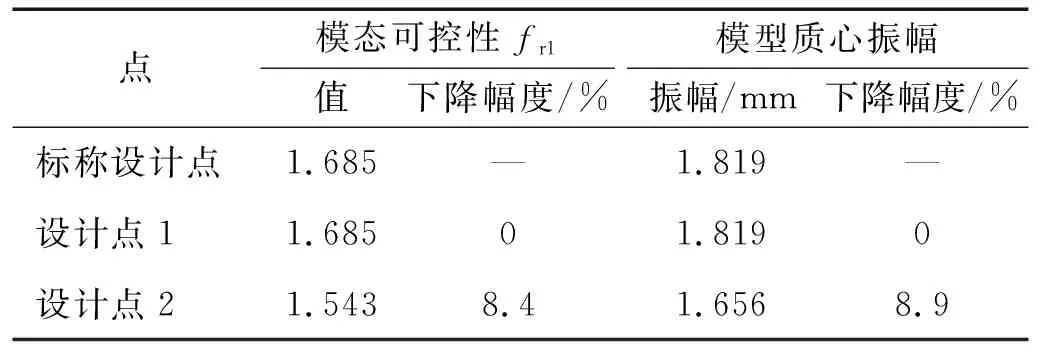
表5 作动器效率预测结果与仿真结果对比

5 结 论

(1) 在风洞模型主动减振结构设计和敏感性分析时，应用本文给出的相对可控性表征方法来定量描述作动器效率，能够更好地对主动减振结构的减振效果做出合理预期。

(2) 对于双弹性铰链主动减振结构，上、下铰链的长度、厚度、宽度等参数是通过改变铰链拉伸刚度和弯曲刚度来影响作动器效率的。降低铰链的弯曲刚度，可以提高主动减振结构的作动器效率，但附带引起的铰链拉压刚度降低却会削弱压电作动器的输出能力。

(3) 铰链弯曲刚度对主动减振结构的作动器效率影响呈近似线性，而铰链拉伸刚度对作动器效率影响却分为低于临界拉伸刚度时的高敏感区和高于临界拉伸刚度时的低敏感区。在铰链设计时，应在拉伸刚度的低敏感区内时选取设计参数。