双层石墨烯中的偶数分母分数量子霍尔态*

李庆鑫 黄焱 陈以威 朱雨剑 朱旺 宋珺威 安冬冬 甘祺康 王开元 王浩林† 麦志洪Andy Shen 郗传英 张警蕾 于葛亮‡ 王雷††

1) (南京大学物理学院,固体微结构物理国家重点实验室,南京 210093)

2) (南京大学,人工微结构科学与技术协同创新中心,南京 210093)

3) (中国科学院强磁场科学中心,合肥 230031)

4) (湖北九峰山实验室,武汉 430206)

在半填充的朗道能级,复合费米子手征p 波配对的Moore-Read 态具有e/4 的分数激发,其中部分这种准粒子服从非阿贝尔统计,有望用于实现拓扑量子计算.双层石墨烯由于其电子的SU(4)对称性和电场对其性质的方便调控性,成为研究多分量量子霍尔态的理想平台,是实现非阿贝尔统计的候选者.本文利用干法转移技术制备了双层石墨烯/氮化硼异质结,通过电学输运测量展示了双层石墨烯在调节外电场和磁场下的量子霍尔态行为.在强磁场下,观测到了朗道能级填充因子为—5/2,—1/2,3/2 的伴随着量子化霍尔电导的不可压缩态.随着磁场继续增强,这些偶数分母量子霍尔态特征先增强再减弱,对应朗道能级波函数的极化.实验结果暗示观察到的这些偶数分母分数量子霍尔态属于由Pffafian 波函数描述的拓扑态.

1 引言

二维电子系统中的多体关联与非平庸拓扑导致了许多新奇的现象,例如分数量子霍尔效应(fractional quantum Hall effect,FQHE)[1].在强磁场下,高简并度的朗道能级形成几乎零色散的平带,增强的库仑作用(U～,磁长度lB=,h是普朗克常数,e是元电荷,B是磁感应强度)与规范不变性共同作用使电子与磁通形成复合费米子[2,3],表现出分数量子化的霍尔电导.当朗道能级被半填充时,复合费米子感受到的有效磁场变为零,从而形成可压缩的复合费米子液体[4].这种费米液体同样可能在复合费米子库珀配对下失稳,被预言形成类似拓扑超导的Moore-Read 态,其激发是遵循非阿贝尔统计的马约拉纳模式[5,6].

在GaAs 量子阱朗道能级ν=5/2 处[7,8],人们首次观测到半填充处的FQHE,但一些实验结果与预言的Moore-Read 态行为并不完全一致[9-11],仍缺乏支持非阿贝尔统计的直接证据.最近在单层石墨烯N=0 朗道能级[12]与更高的朗道能级[13]中同样出现了半填充处的不可压缩态,而后者被解释为可能的非阿贝尔态.与GaAs 体系不同,石墨烯中的低能电子具有自旋和能谷简并构成的SU(4)对称性[14],其朗道能级由多分量波函数描述.在部分填充的朗道能级,这些自由度的交换能与塞曼能对决定石墨烯的量子霍尔行为非常重要[15].然而单层石墨烯中的狄拉克点受C2z对称性保护,谷间带隙无法被外界打开,这大大限制了人们对单层石墨烯中量子霍尔态的调控能力.双层石墨烯中,由于缺少C2z对称性,可以通过调节垂直电场来控制两个能谷间的能量差从而方便地调控量子霍尔态到可压缩态的转变[16-18],同时利用磁场适当地调节轨道波函数结构,双层石墨烯中有可能出现Moore-Read 态[19-21].之前有相关报道用电容设备测量并展示了双层石墨烯中的偶数分母分数量子霍尔态,但是由于测量方法的限制并没有能得到像电输运一样能反映横向电导平台的数据[22].最近也有研究者在六方氮化硼封装的双层石墨烯中用电输运的方法测到了一系列偶数分母分数量子霍尔态[23],但是在高于31 T 的强磁场下却缺乏相关的研究,而一直以来偶数分母分数量子霍尔态在高场下的变化趋势为猜测其是Pfaffian 或anti-Pfaffian 态的一个重要依据,因此十分重要[20].本文制备了高质量的双层石墨烯双栅器件,通过使用少层石墨代替传统的合金接触,获得了原子级平整的接触电极.在强磁场下,施加一定的电位移场调节谷塞曼能,观测到了一系列鲁棒的偶数分母分数量子霍尔态,为未来进行干涉实验检验非阿贝尔统计性质提供了研究平台.

2 实验与讨论

图1(a)展示了器件的结构示意图,通过“拾取法”转移法[24]拾取六方氮化硼对双层石墨烯进行封装,这不仅为双层石墨烯提供了平整的衬底还使其隔绝空气环境,提高了器件迁移率.同时在双层石墨烯的上下方使用石墨作为栅极,相比于金属栅极减少了合金蒸镀时引入的无序和缺陷.另外在双层石墨烯的两边使用少层石墨与双层石墨烯接触,再用金属电极与少层石墨完成边缘电接触,极大地降低了接触电阻,提升了器件的质量.这种范德瓦耳斯层状结构允许上下栅极的独立使用,从而可以分别调控双层石墨烯中的载流子浓度n和电位移场强度D.载流子浓度为n=(CTVT+CBVB)/e-n0,电位移场强度表示为D=(CTVT-CBVB)/2ε0-D0(CT和CB分别为上、下层电介质单位面积的电容,VT和VB分别为上、下层栅极所施加的电压,n0和D0为剩余载流子浓度和剩余电位移场).图1(d)给出了T=1.5 K 时,双层石墨烯器件在电位移场强度D和磁场强度B都为 0 的情况下,纵向电阻Rxx随载流子浓度n的变化关系.根据狄拉克峰的半峰宽可以估算出器件中缺陷和杂质的量级3.5×1010cm-2,迁移率为106cm2/(V·s).

图1 器件结构和双层石墨烯里的分数量子霍尔态 (a) 器件结构图;(b) 温度T= 1.5 K 与磁场B= 8 T 时,纵向电阻Rxx 随电位移场D 和填充因子ν 的变化图(红色虚线表示以3 为分母的分数态) (c) 双层石墨烯N=0,1 朗道能级中四原子上波函数分布图;(d) 温度T=1.5 K,电位移场D= 0 V/nm 与磁场B= 0 T 时,纵向电阻Rxx 随载流子浓度n 的变化Fig.1.Device structure and FQH states for in bilayer graphene (BLG): (a) Device schematic;(b) Rxx versus ν and D at B= 8 T and T= 1.5 K (The red dotted lines represent the fractional state with 3 as the denominator);(c) the schematic of wave function distribution on the four atomic sites of BLG for the N=0,1 Landau orbital states;(d) Rxx versus n at D= 0 V/nm,B= 0 T,and T= 1.5 K.

图1(b)展示了T=1.5 K 时双层石墨烯器件在固定垂直磁场下(B=8 T)纵向电阻Rxx随朗道能级填充因子ν(ν=nh/(eB),n是载流子浓度)和电位移场强度D的变化关系.我们观察到一系列在外场和库仑相互作用下SU(4)对称性破缺导致的整数量子霍尔态,对应于纵向电阻Rxx出现极小值.其次,在ν=—7 到—4 之间和ν=4—8 之间,观察到以3 为分母的分数量子霍尔态(图1(b)中用红色虚线标识),这说明器件具有很高的质量.在|v|＞ 4 范围内,同一朗道能级中填充因子为奇数的量子霍尔态出现在所有电位移场不为零的区域,而填充因子为偶数的量子霍尔态在有限的电位移场下消失,这是因为电位移场会改变单粒子谷塞曼能导致朗道能级出现交叉[16,17].而在|ν|≤4 区域内,ν=±1 处在D=0 V/nm 与有限大的电位移场时发生了压缩态与不可压缩态的转变;ν=±2处,在电位移场十分接近零时发生相变;ν=±3 处的相变只发生在D=0 V/nm 处,这些现象源于双层石墨烯特殊的朗道能级结构[18,25].与非狄拉克型色散的二维量子阱(例如GaAs 量子阱)不同,双层石墨烯的N=0 与N=1 朗道能级是简并的[26].图1(c)展示了双层石墨烯中K谷的零能朗道能级波函数,K′谷的波函数可同时改变层与子格占据位置获得.其中N=0 轨道等同于非相对论粒子的n=0 朗道能级波函数,而N=1 轨道则是n=0与n=1 波函数的组合.增加磁场不仅会解除轨道的简并,还会改变N=1 轨道中两种态的占据权重,特别是,非阿贝尔的 Pfaffian 态被预言出现在n=1 轨道上[5].另外轨道的简并性在双层石墨烯中也引入了不可忽略的朗道能级散射,这对稳定可能出现的拓扑相非常重要[19,27,28].

在更高的磁场下,我们在双层石墨烯中进一步观测到了更多奇数分母的分数量子霍尔态以及出现在半填充处的分数量子霍尔态(图2—图4).图2(a)展示了当电位移场为D=—0.12 V/nm,填充因子ν=1—2 时,纵向电阻Rxx随填充因子ν和磁场B变化的二维图.与图1(b)相比,可以看到在1+1/5,1+2/5,1+3/7 及其共轭处和1+1/2处出现了一系列新的不可压缩态.为分析这些分数态,固定磁场在33.75 T,作出了纵向电阻Rxx和横向电导σxy随填充因子ν的变化图(图2(b)).可以看到在1＜ν＜2 内,当朗道能级处于上述分数填充时,横向电导以e2/h为单位产生量子化的平台,其平台值为σxy=νe2/h.出现这些特征的分数态大致上可分为两类: 一类是可以由Jain 波函数描述的复合费米子态.根据复合费米子理论,每个复合费米子由一个电子携带2p个量子磁通 (ϕ0=h/e)组成,且这些复合费米子[2]感受到有效磁场为B*=B-2pnϕ0,形成等效的“朗道能级”,有效填充因子ν*=nh/(eB*),因此这类分数态的填充因子可以描述为ν=1+ν*/(2pν*±1) (1＜ν＜2),其中p是整数.另一类是复合费米子无法描述的偶数分母分数量子霍尔态(ν=3/2 态),与GaAs 体系中被预测为anti-Pfaffian 态的ν=5/2 态[27,29]不同的是,本文结果表明复合费米子态在3/2 附近是粒子空穴对称的,并且最近研究报道ν=3/2 这类态可能为Pfaffian 态[22].

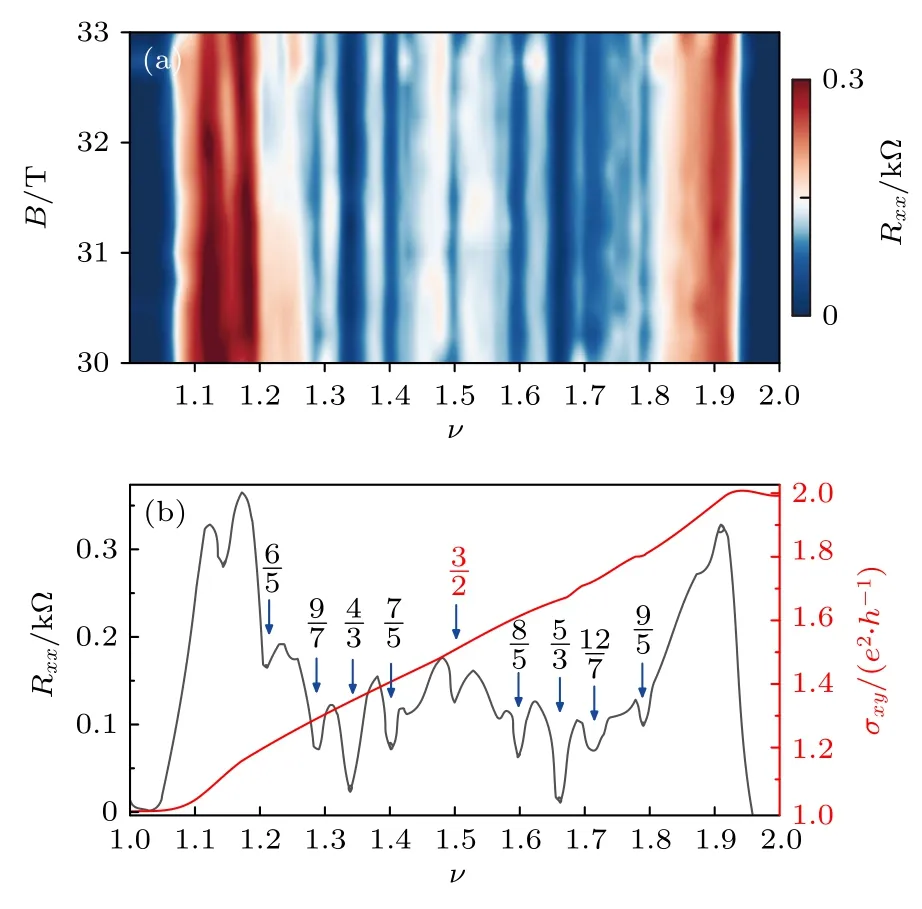
图2 1 ＜ν＜ 2 时的分数量子霍尔态 (a) 温度T=0.3 K与电位移场D =—0.12 V/nm 时,纵向电阻Rxx 随填充因子ν 和磁场B 变化的二维图;(b) 固定温度T=0.3 K、电位移场D =—0.12 V/nm 与磁场B=33.75 T 时,纵向电阻Rxx (黑色)和横向电导σxy (红色)随ν 的变化Fig.2.FQH states for 1 ＜ν＜ 2: (a) Rxx as a function of ν and B at T =0.3 K and D=—0.12 V/nm;(b) Rxx (black)and σxy (red) versus ν at B =33.75 T,D=—0.12 V/nm and T =0.3 K.

图3 和图4 分别给出了填充因子—1＜ν＜0 和—3＜ν＜—2 时,Rxx随B和ν变化的二维图,以及在固定磁场下Rxx和σxy随ν的变化.在ν＜0 时,虽然在—1＜ν＜0 和—3＜ν＜—2 的半填充处都出现了明显的不可压缩态,对应着Rxx表现为极小值,但是相比ν=—1/2,ν=—5/2 处Rxx下降幅度更小(ν=—5/2 处Rxx下降了80 Ω,而ν=—1/2处Rxx下降了800 多欧姆),因此我们认为出现在ν=—1/2 的不可压缩态要比出现在ν=—5/2 处的更强,这可能是受朗道能级之间的混合,或是体系的无序和杂质的影响,与之前的报道吻合[23].除此之外,在ν=—12/5,ν=—1/7 和ν=—1/5 处的复合费米子态表现出明显的粒子空穴不对称行为,这也暗示存在较强的朗道能级混合.

图3 —1＜ν＜ 0 时的分数量子霍尔态 (a) 温度T=0.3 K与电位移场D=—0.12 V/nm 时,纵向电阻Rxx 随填充因子ν 和磁场B 变化的二维图;(b) 固定温度T=0.3 K、电位移场D=—0.12 V/nm 与磁场B =31.58 T 时,纵向电阻Rxx (黑色)和横向电导σxy (红色)随填充因子ν 的变化Fig.3.FQH states for —1＜ν＜ 0: (a) Rxx as a function of ν and magnetic field B at T =0.3 K and D =—0.12 V/nm;(b) Rxx (black) and σxy (red) versus ν at B=31.58 T,D =—0.12 V/nm and T =0.3 K.

图4 —2＜ν＜—3 时的分数量子霍尔态 (a) 温度T =0.3 K与电位移场D=—0.12 V/nm 时,纵向电阻Rxx 随填充因子ν 和磁场B 变化的二维图;(b) 固定温度T=0.3 K、电位移场D=—0.12 V/nm 与磁场B =28 T 时,纵向电阻Rxx 和横向电导σxy 随ν 的变化Fig.4.FQH states for —2＜ν＜—3: (a) Rxx as a function of filling factor ν and magnetic field B at T= 0.3 K and D =—0.12 V/nm;(b) Rxx (black) and σxy (red) versus ν at B=28 T,D =—0.12 V/nm and T =0.3 K.

为了更清楚地理解半填充处不可压缩态的性质,研究了在不同磁场下这些分数量子霍尔态的演化.图5(a)—(c)分别给出了在—3＜ν＜—2,—1＜ν＜0 和1＜ν＜2 内,不同磁场下纵向电阻Rxx随填充因子ν的变化.在—3＜ν＜— 2 区间内,磁场升到27.6 T 时,可以看到在ν=—5/2 处电阻开始出现极小值,表明形成了不可压缩态,并随着磁场的增高而变强;当磁场增大到28.8 T 时,纵向电阻Rxx降低的幅度达到最大,意味着此时体态能隙达到最大;而接下来继续升高磁场,不可压缩态的能隙开始减小(图5(a)).同样,在—1＜ν＜0 和1＜ν＜2 区间内,随着磁场的不断变大,出现在半填充处的不可压缩态也呈现出先增强后减弱的趋势,并分别在34 T 和30 T 达到最强(图5(b)和图5(c)).这些结果表明出现在双层石墨烯第一朗道能级内的偶数分母的分数量子霍尔态对磁场有强烈的依赖性,并且只出现在一段磁场区间中,过高或过低的磁场都会削弱半填充处的不可压缩态,与之前的理论工作一致[20].当磁场增加时,库仑能与回旋能量之比增加导致偶数分母的FQHE 更强,而当磁场增加到很大时,朗道能级波函数逐渐被极化到n=0 轨道,更倾向于形成复合费米子液体[19].

图5 不同磁场下分数量子霍尔态的演化 (a)—(c) 分别描述了温度T= 0.3 K 与电位移场D =—0.12 V/nm 时,不同磁场下纵向电阻Rxx 随填充因子ν 的变化 (为了能在不同磁场下显示更清楚,每条曲线都加入了偏移量),其中(a) —3＜ν＜—2,(b)—1＜ ν＜0 和(c) 1＜ν＜2Fig.5.Evolution of FQH states under different magnetic fields: (a)—(c) Rxx as a function of filling factor ν at T=0.3 K and D=—0.12 V/nm for different magnetic field,corresponding to filling fractions spanning (a) —3＜ν＜—2,(b)—1＜ν＜0,and (c) 1＜ν＜2.

3 结论

综上所述,我们在双层石墨烯器件中利用电输运测量方式观察到了一系列朗道能级处于半填充的量子霍尔态,对应的填充因子为ν=—5/2,—1/2,3/2.在一定磁场范围内,半填充的量子霍尔态的强度会随磁场增加而变强,到达临界磁场后,量子霍尔态的强度随磁场的增加逐渐下降.相比于之前的文献[22]报道,这些量子霍尔态具有更明显的特征,不仅纵向电阻出现极小值,横向电导也出现量子化的电导平台.但是受限于我们的测量手段与器件结构,电中性的边缘激发模式无法包括在本文数据中,这些不可压缩态的性质仍然需要进一步的研究来理解.期望未来的研究能够改进器件结构,利用双层石墨烯的高度可调控性进行边缘态隧穿实验[30]、热输运测量[9]、磁学测量[31]、准粒子干涉实验[32,33]等来直接探测这些基态的低能激发谱与准粒子的统计性质.

感谢中国科学院合肥物质研究院强磁场科学中心提供磁运输测量仪器,感谢中国科学院强磁场科学中心郗传英老师和钱英才同学在实验上对我们的帮助.