杨振宁先生和冷原子物理

翟荟

(清华大学高等研究院,北京 100084)

早在20 世纪50 年代,杨振宁先生和他的合作者们就意识到,稀薄中性量子气体中最主要的相互作用效应可以被s-波散射长度来描述,从而可以得到不依赖于粒子间相互作用的细节的普适描述.这一洞见奠定了量子气体的理论基础.他们还由此给出了玻色气体基态能量的表达式,后来被称为“Lee-Huang-Yang 修正”.实验物理学家克服种种困难,在近40 年后的1995 年,才将冷原子气体冷却到量子简并.此后,冷原子物理展示出来种种优势,包括相互作用和维度的可调控性以及测量的精密性,这使之成为研究量子多体物理的理想平台之一.多个冷原子实验观测到“Lee-Huang-Yang 修正”的效应.通过有效地降低系统维度,冷原子实验对一维体系的研究,还证实了杨先生在20 世纪60 年代提出的Yang-Yang thermodynamics.2010 年左右,年逾八旬的杨先生再次研究一维可解模型,他发现的一维多分量费米子系统的极限行为,又很快被冷原子实验证实.通过内态调控产生等效的人工维度,冷原子体系还可以模拟高维体系的物理,其中包括实验模拟了杨先生于20 世纪70 年代提出的SU(2)非阿贝尔规范场中的Yang monopole 这一拓扑解.这些冷原子物理的进展,展示了杨先生的这些工作不仅具有理论的深度,还对实际实验的发展具有长远的影响力.

1956 年,杨振宁先生和李政道先生[1]写下了著名的“弱作用宇称不守恒”的论文,随后于1957 年他们因此获得了诺贝尔物理学奖.可能大家并不太知道,就在同一时期,他们还在研究一个量子统计物理的问题—具有硬球相互作用的稀薄气体的量子多体物理.差不多在宇称不守恒论文发表的同时,他们还将另一篇文章投稿到了Physical Review[2].这篇文章总结了他们已经得到的关于稀薄硬核玻色或费米气体的结果.这其中就包括该玻色子多体系统基态能量的表达式[2]:

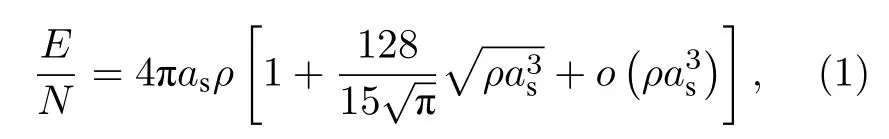
式中,ρ是玻色子的密度,as是粒子间的s-波散射长度.次年,杨振宁先生和李政道先生、黄克孙先生[3]又发表了另一篇文章,他们利用赝势方法系统地给出了研究硬球玻色模型的计算细节,计算得到了和(1)式同样的关于基态能量的表达式.这一结果后来被称为“Lee-Huang-Yang 修正”.2012 年,在庆祝杨先生90 华诞的活动上,清华大学赠给了杨先生一个礼物: 精致的黑色立方体的四面镌刻着杨先生在粒子物理、场论、统计物理和凝聚态物理四个方面的13 项杰出的贡献.其中统计物理的那一面,“1957 Bosons”指的就是这个工作[3].

杨先生和他的合作者在1956—1958 年期间的一系列工作,其实已经开拓了一个全新的领域.但他们还需要等待40 年,才能看到这个领域真正的诞生.这个领域现在被称为“量子气体”或“超冷原子气体”.近四十年后的1995 年,在碱金属原子气体中实验实现了玻色-爱因斯坦凝聚,标志着这一领域的诞生[4,5].

而在当时,他们的研究动机主要是为了理解液氦超流.但是,液氦是一个液体,氦原子之间的相互作用非常强,而且在液氦中,氦原子相对距离比较近,在这个距离上,原子间相互作用势较为复杂.杨先生和他的合作者们在探索一个相对简单些的情形: 一方面,原子间的相互作用在这个多体系统中仍然扮演着重要的作用;另一方面,处理相互作用的所需的近似方法的有效性是可控的.在文献[6]中,他们写道:

“ It is physically obvious that a complete knowledge of the detailed interaction potential is often not necessary for a satisfactory description of the system.For example,when a state of the many-body system is such that the particles are so far apart from one another that their fields of force do not appreciably overlap,their mutual influence is essentially determined by the asymptotic wave functions,which are directly related to the phase shifts.Furthermore,under certain conditions only a few phase shifts are important.For example,at low energies,all but the s-wave phase shift are negligible.The proposed formulation would provide a natural framework in which an approximation such as this could be systematically carried out.”

今天看来,这一段论述仍然非常精彩而重要.这一段论述所体现的洞见揭示出中性原子量子气体这一系统独特而重要的优势.和液体所不同的是,气体是稀薄的、密度低.和电子所不同的是,中性原子间的相互作用势是短程的.因此,在原子气体中,原子间的间距远大于相互作用的力程.在这样的情形下,相互作用效应本质上被波函数的渐近行为所决定,而对于短程势而言,波函数的渐近行为又体现在散射相移上.在低能下,s-波散射相移起到决定性的作用,而s-波散射相移又主要被s-波散射长度决定.因此,对量子气体来说,并不需要知道原子间相互作用复杂的细节,最主要的相互作用的物理可以完全由s-波散射长度来刻画.正因为如此,量子气体中的相互作用效应常常能得到简洁而普适的刻画.这正是量子气体成为一个研究量子多体物理的理想平台的重要原因.1995 年超冷原子气体实验实现以后,这一优势被广为认同.而杨先生和他的合作者们在此40 年前就已经将其阐述得非常清楚了.

意识到as是描述原子间相互作用的最重要的参数之后,就不难发现,是一个无量纲的参数.当这个参数是一个小量时,就可以将基态能量等物理量按照这个参数展开,这就得到了(1)式.(1)式中第1 项来自于平均场效应,它描述的是一个原子感受到的其他原子平均的一个相互作用效果.因此,这一项正比于原子的平均密度.第2 项是完全的量子效应,它代表的是超越平均场之外的量子修正.这一修正就是“Lee-Huang-Yang 修正”.这一项也有明确的物理意义,那就是真空零点能.在无相互作用的情况下,该系统的基态是所有的玻色子都凝聚在零动量上.有相互作用之后,一对玻色子可以从零动量被散射到正负相反的有限动量,这就产生了所谓的Bogoliubov 元激发.在每一个动量上,都有一个Bogoliubov 元激发的模式,而由于量子涨落,每一个元激发模式都有一个非零的零点能.也就是说,在零温下,即便每个Bogoliubov 元激发的模式都没有实际的占据,这些零点能也会对系统的基态能量产生贡献.对所有动量上这些零点能的求和,就构成了“Lee-Huang-Yang 修正”.正因为如此,我们说“Lee-Huang-Yang 修正”代表了真空的零点能.而且,这个求和会表现出紫外发散,因而需要被重整化.为了消除发散,杨先生他们用文献[6]中引入的赝势方法来进行重整化,最终得到了一个有限的结果.

虽然这些奠基性的理论在20 世纪50 年代就已经提出来了,但是,离实验实现量子气体还需要40 年的时间.这里有很多实验上的困难需要被克服,为此还有很多实验技术需要被发明.首先,需要保持这个系统足够稀薄.只有这样,才能使得两体碰撞相对三体碰撞更占主导.这样的话,系统才能在气态达到热平衡,而不会形成化学上更稳定的分子态,甚至成为固体.其次,需要防止气态原子附着在腔壁上.这个问题被20 世纪80 年代发展的磁束缚和90 年代发展的激光束缚所解决.再则,因为气体很稀薄,所以要达到量子简并,就需要更低的温度.从20 世纪70—80 年代先后发展出来的激光冷却和蒸发冷却,成为解决这一问题的重要手段.随着这些技术手段的不断成熟,终于在1995 年,碱金属玻色原子气体率先被冷却到量子简并,并在其中观测到玻色-爱因斯坦凝聚的现象[4,5],这一成就在2001 年获得了诺贝尔物理奖[7].

从1995 年以来,超冷原子物理得到了飞速的发展[8].杨振宁先生从一开始就极力提倡和推动这一领域,特别是建议中国学者积极投身到这一研究方向.在玻色-爱因斯坦凝聚实验实现后不久,杨先生自己也立刻回到了这个领域开展研究,又发表了多篇研究论文[9,10].20 世纪50 年代早期的工作主要考虑的是热力学极限下的均匀体系,而在实验中,由激光或磁场产生了一个谐振子势阱,以此来束缚原子.杨先生等就将20 世纪50 年代的一些早期的结果推广到了有谐振子外势的情况[9,10].

随着冷原子物理的发展,很快还展现出其他几方面的优势[8].一是可调控性.例如,原子间的相互作用可以被一种称为Feshbach 共振的机制来调节;系统的维度也可以被光晶格等光和原子相互作用的手段来操控.二是测量的高精度.例如,为了发展原子钟,需要将频率测准到很高的精度.这一技术就可以被迁移到研究量子多体物理,例如将系统的相互作用能测准到一个很高的精度.

利用冷原子体系的这些优势,一系列的实验很快就观测到“Lee-Huang-Yang 修正”的效应[11-16].因为“Lee-Huang-Yang 修正”是按照展开的第二阶项,因此,如果太小的话,这一项的效应就很难被观测到.也就是说,要想观察到“Lee-Huang-Yang 修正”的效应,需要适当地把as调大一些.而Feshbach 共振正是这样一个调节散射长度的手段.另一方面,冷原子体系的能量可以通过集体激发的频率、密度分布、压强或谱学等方法来测量[11-16].所有这些实验测量都发现,随着的增大,实验测得的能量明显地偏离平均场的结果,而和包含了“Lee-Huang-Yang 修正”的结果更为吻合.图1 展示了一个有代表性的实验结果.

图1 “Lee-Huang-Yang 修正”的实验证实.纵轴压强 h 反映了系统的状态方程,横轴是 µa3/g.这里,a 就是文中的散射长度 as;µ 是巨正则系统的化学势;g=4πℏ2a/m,m是原子的质量.黑色点是实验结果,红色实线是加入“Lee-Huang-Yang 修正”的理论结果,黑色实线是蒙特卡罗计算的结果,红色虚线是没有加入“Lee-Huang-Yang 修正”的平均场结果.插图是弱相互作用区域的结果 [15]Fig.1.Experimental observation of the Lee-Huang-Yangcorrection.The equation-of-state,measured through the pressure h,is plotted as a function of µa3/g.Here a is the s-wave scattering length as in the text.µ is the chemical potential in the grand canonical ensemble.g=4πℏ2a/m .The solid red line is theoretical result with the Lee-Huang-Yang corrections,and the solid black line is the result obtained by quantum Monte Carlo simulation.The red dashed line is the mean-field result without including the Lee-Huang-Yang corrections.The inset is a zoom-in plot of the weakly interacting regime[15].

在冷原子体系中,除了相互作用的强度可以调节以外,系统的维度也可以调控.特别地,对维度的调控使实现一维多体系统成为可能.在20 世纪60 年代,杨先生利用Bethe 提出的Bethe Ansatz方法[17],对一维体系的多体问题做了大量的研究工作.其中最为著名的工作就是他求解了一维接触相互作用的自旋-1/2 的费米子多体问题[18].这导致了著名的Yang-Baxter 方程,后来在数学物理中产生了重大的影响.在20 世纪60 年代,这些问题被看成纯粹的数学物理问题.而40 年后,冷原子物理的发展使得这些问题成为非常实际的问题.

1969 年,杨先生和他的弟弟杨振平教授[19]一起求解了一维接触相互作用的玻色子体系有限温度的统计问题.这一工作在杨先生的13 项杰出成就中也被提到,被标注为“1969 Finite Temperature”.此前,Lieb 和Liniger[20]求解了这个系统的基态问题.杨先生的工作解决了整个有限温度的问题.这种有相互作用的多体统计物理问题可以被严格求解,也是一个很少见的情况.这一结果被称为Yang-Yang thermodynamics.Yang-Yang thermodynamics 的预言也在冷原子体系被实验所证实.如图2 所示,无论是测量的密度分布还是动量分布,都和Yang-Yang thermodynamics 的预言非常吻合[21].

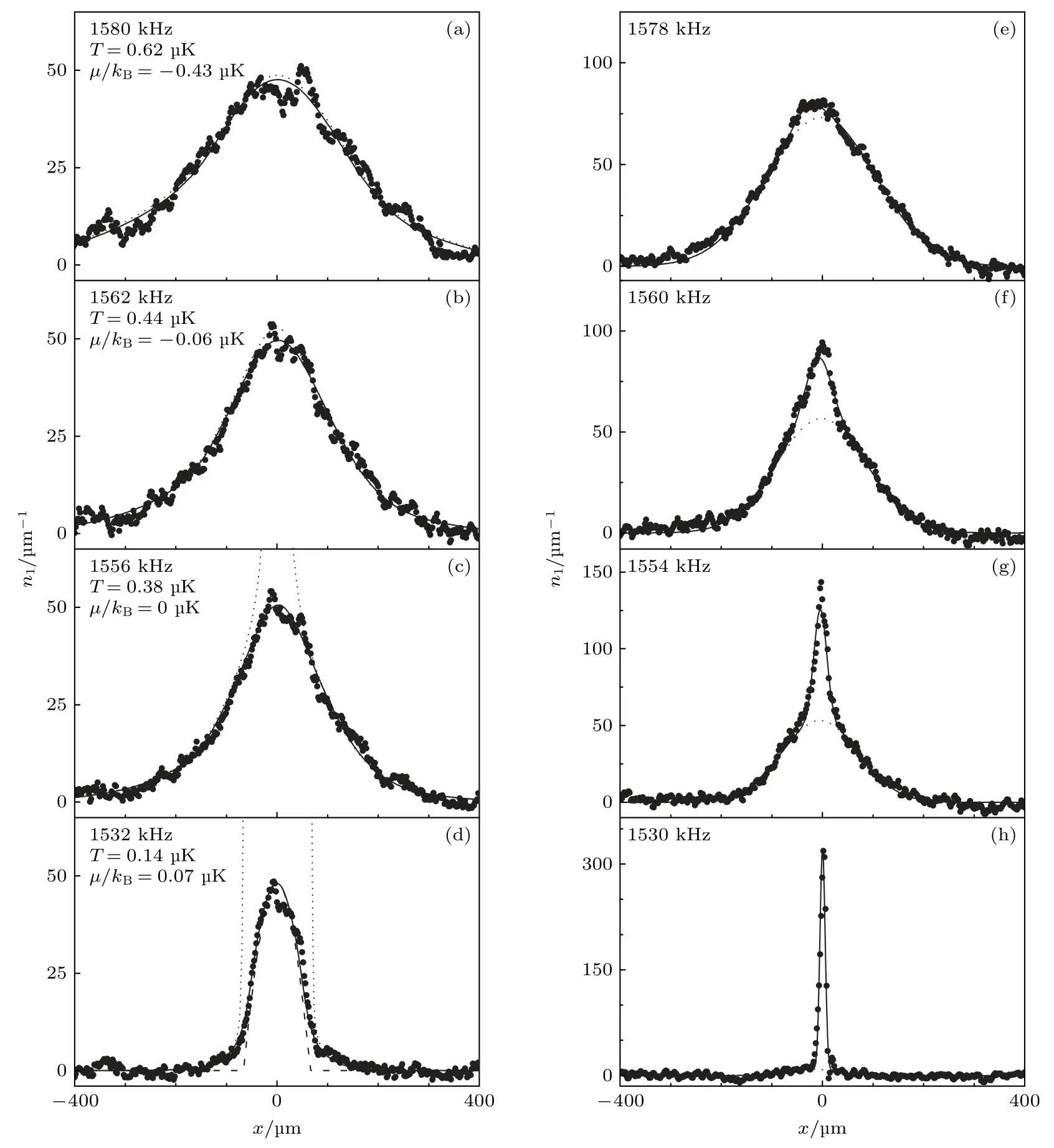
图2 Yang-Yang Thermodynamics 的实验证实 (a)—(d) 原位成像的密度分布;(e)—(h) 动量分布.实线是Yang-Yang Thermodynamics 的理论预言,虚线是无相互作用玻色子的结果.黑色的点是实验数据点[21]Fig.2.Experimental observation of Yang-Yang thermodynamics: (a)—(d) The in-situ density distribution;(e)—(h) the momentum distribution.The solid lines are obtained from the Yang-Yang thermodynamics and the dashed lines are the results of non-interacting bosons[21].

2010 年左右,杨先生已年逾八旬.他对冷原子物理在一维系统的这些进展非常感兴趣,重新回来研究这方面的课题.他和尤亦庄一起,求解了一维N个分量的费米子系统的状态方程.他们发现,当内态数目N趋向于无穷大时,这个多分量费米体系的状态方程趋于一个单分量玻色子体系的状态方程[22].佛罗伦萨的一个冷原子实验组很快就实验证实了这个理论预言[23].实验上,他们通过测量集体激发模的频率来反映系统的状态方程.他们通过改变内态的数目,测量这个激发模的频率,实验结果如图3 所示.他们发现,当内态数目增加时,这个激发模的频率趋近于单分量玻色子系统中的同种激发模的频率[23].这一实验结果和杨先生论文的预言非常吻合[22].佛罗伦萨的实验文章中引用了杨先生和尤亦庄的论文,并写道:

图3 N 分量一维费米气体的实验结果.β=ωB/ωx,其中 ωB 是测得的沿方向系统呼吸模的频率,ωx 是沿 方向谐振子势阱的频率.横轴是费米子内态的数目N.其中正方形方块是实验数据,圆圈是理论预言.上面的横线是无相互作用(N=1)费米子的情况;下面的横线是单分量玻色子的情况,即 N→∞ 的极限情况[23]Fig.3.Experiments on N-component one-dimensional Fermi gas.β=ωB/ωx,where ωB is the breathing mode frequency along and ωx is the harmonic trap frequency along .This frequency is plotted as a function of the number of fermion components N.The squares are experimental data and the circles are theoretical predictions.The upper horizontal line shows the theoretical value for non-interacting Fermi gas (N=1) and the lower line shows the result for spinless bosons,as N→∞ limit[23].

“ This bosonic limit forN→∞ is aremarkable property of multi-component 1Dfermions that has been pointed out theoretically only very recently and that our experimental system is capable to clearly evidence.”

冷原子体系的可调控性,不仅可以等效地降低系统的维度,而且还可以等效地提升系统的维度.降低系统的维度通常是通过光晶格等方法产生一个束缚势,限制原子在其他方向的运动.而另一方面,通过光和原子的相互作用还可以耦合原子不同的内态[24].如果把这些耦合起来的内态等效地看成一个“人工维度”的话,就可以等效地提升系统的维度,从而利用冷原子体系去实现一些高维空间的物理.

1954 年,杨先生和Mills[25]一起提出了非阿贝尔规范场理论,后来被称为Yang-Mills 理论.他们将电磁理论这一U(1)规范理论推广到非阿贝尔的情形.Yang-Mills 理论后来成为统一电磁相互作用、弱作用和强作用的标准模型的基础.在三维空间电磁理论这一U(1)阿贝尔规范理论中,存在著名的Dirac 磁单极子解.Dirac 磁单极子是电磁场的拓扑缺陷.数学上,刻画这一拓扑缺陷的工具是第一类陈数:

第一类陈数是磁场B或者说阿贝尔规范场的场强Fµν定义在三维空间中一个二维闭曲面S2上的积分.1978 年,杨先生[26]将Dirac 磁单极子解推广到SU(2)非阿贝尔规范场的情况.这个情况下的磁单极子解后来被称为Yang monopole.Yang monopole 存在于五维空间中,它的拓扑特性是由第二类陈数来刻画的.第二类陈数是定义在五维空间中一个四维闭合曲面S4上的积分,它的表达式是

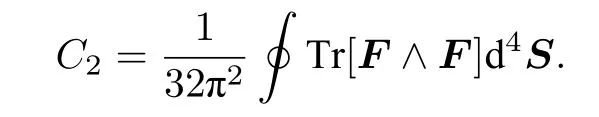
这里联系非阿贝尔规范场的场强F和规范式A的公式,就是杨先生和Mills 文章中给出的著名的公式[25]:

SU(2)非阿贝尔规范场中的Yang monopole 具有非零的第二类陈数,但是其第一类陈数总是为零.

美国国家标准局的实验组用耦合原子内态的方法来模拟空间维度,从而来模拟Yang monopole[27].特别地,他们将4 个不同的内态用5 个独立的参数耦合起来,并通过巧妙的设计,使得这5 个参数恰巧位于一个4 维球上.他们测量了这个体系的第一类陈数和第二类陈数.如图4 所示,他们发现第一类陈数总是等于零,而第二类陈数会随着Yang monopole 移出球面而从1 变到0.

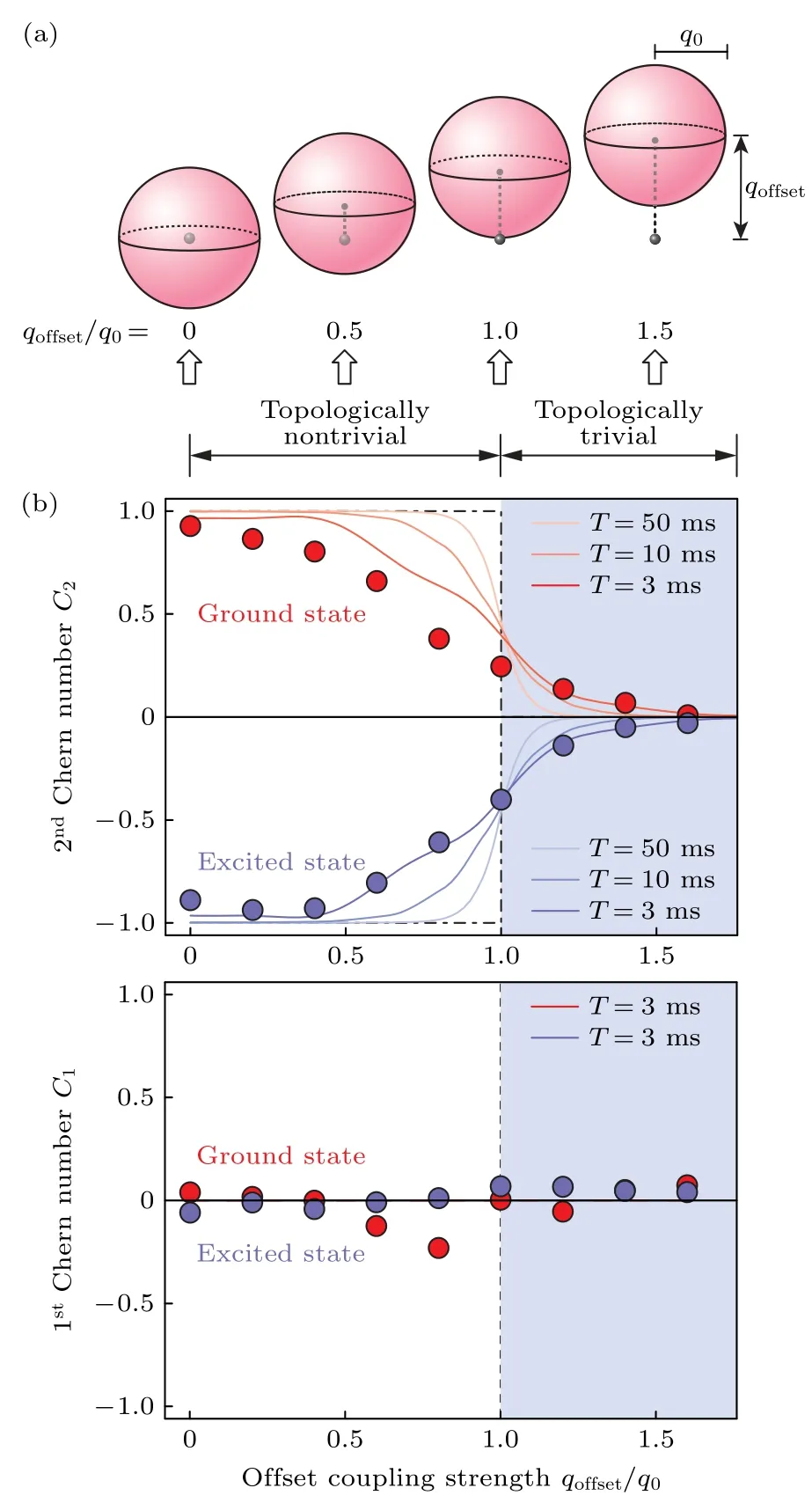
图4 实验观测到Yang monopole (a) 随着Yang monopole移入或移出球面,系统拓扑的变化;(b) 第一类陈数(下图)和第二类陈数(上图).第一类陈数总是零.第二类陈数随着Yang monopole 移出球面,从1 变成0[27]Fig.4.Experimental observation of Yang monopole: (a) Illustration of the topological transition when the Yang monopole moves out of the sphere;(b) the first (lower) and the second (upper) Chern number.The first Chern number is constantly zero and the second Chern number changes from unity to zero as the Yang monopole moves out of the sphere[27].

杨先生的工作先于实验近40 年,奠定了冷原子物理的理论基础.杨先生在20 世纪50—70 年代的多个理论工作,时隔几十年之后,被冷原子实验所证实.杨先生年逾八旬,再重新研究相关理论问题,提出的新理论又很快被实验证实.

自冷原子这一领域从1995 年诞生以来,杨先生一直关注重视这个领域,多次公开谈到这是一个有发展前途的研究方向.二十多年来,冷原子物理的发展,凭借其高度的可调控性和测量的精确性等优势,不仅证实了杨先生的一系列理论预言,而且在量子多体物理,特别是量子多体非平衡动力学方面,取得了很多令人瞩目的成果.此前,针对量子多体系统的研究,主要是基于固体材料的凝聚态物理研究的内容.近年来,冷原子量子气体已成为研究量子多体物理的另一个重要平台.冷原子物理和凝聚态物理既有很大的交集,又高度互补,两者相得益彰.两者的协同发展,会更加丰富我们对量子物质的理解,有益于未来量子科技的发展.

杨先生的这些工作既具有理论的深度,又能和实验结合,并且对实验产生长久的影响力.这不禁让人称奇.杨先生的研究工作,是如何能达到这个境界的,值得我们深思.我想,我们选择一个研究课题,有两方面的考量: 一是这个题目和当前实际物理系统之间的关系;二是这个题目和基本物理问题或其中优美的数学结构的关系.最为重要的是,我们如何能在这两种考量之间取得一个平衡.毫无疑问,杨先生在两者之间取得的平衡,可谓极致.

注: 该文章英文版,收录于World Scientific 出版社将出版的A Festschrift for the Yang Centenary: Scientific Papers.