基于浮箱辅助的大型导管架拆除上浮过程研究❋
赵翊翔,王树青,宋宪仓❋❋
(中国海洋大学1.工程学院; 2.山东省海洋工程重点实验室,山东 青岛 266100)
为了缓解日益增长的能源需求,全世界兴建了大量的导管架平台用以开发海洋油气资源,海洋平台的设计寿命约为20年,根据国际公约和相关规定,导管架平台退役一年内必须进行弃置拆除。随着平台的老龄化趋势不断加快,该问题已成为学术界和工程界的研究热点。
导管架平台的拆除一般分为上部组块拆除和导管架拆除。王儒等[1-2]提出用吊框辅助拆除的方法拆除上部组块,有效解决了索具长度核算、吊点偏心等难题,但当上部组块较大时易造成框架重量过大的问题。阮志豪等[3]针对质量较大的上部组块,基于有限元分析和模型试验结果,验证了利用双船浮托法对上部组块进行拆除的可行性,但受限于双船高度等因素,双船浮托法难以应用于导管架的拆除。传统的导管架拆除方法是浮吊法,可将切割平台起吊至驳船上。罗晓健等[4]以某导管架为例,详细论述了利用浮吊法拆除的流程。吴俊生[5]及Herel等[6]考虑吊点位置的影响,分析了导管架在浮吊拆除过程中的结构强度,并给出最优的吊点位置选择方案。但受限于起重船的起吊能力,浮吊法难以应用于大型深水导管架的拆除。
针对大型深水导管架拆除过程中重量大的难题,近年来已有学者进行了探索。辛晓辉等[7]基于水动力学理论和工程实例,探究了气囊辅助导管架下水的可行性,提出了一种用于导管架与气囊连接的方法,相比于费用昂贵和资源紧张的大型浮吊,气囊助浮法具有较好的经济性。张志远[8]设计了由钢架和气囊相结合并捆扎到导管架上的固定方法,分析了上浮过程的稳定性与运动响应,但文中研究的导管架高度只有34.2 m,且未考虑到气囊安装施工难度大、体积难以变化等弊端,因此该方法在大型导管架上的适用性仍需进一步研究。Berger等[9]介绍了Frigg油田DP2导管架在拆除过程中借助钢制浮箱上浮的方法,阐述了浮箱辅助上浮方法的应用前景,但并没有进行定量分析。针对中、小尺寸导管架的拆除问题,目前国内外已提出比较成熟的应对措施;然而对大型深水导管架拆除问题的研究,却因拆除实例的缺乏而尚处于探索期。
本文针对导管架拆除部分上浮过程,研究了浮箱辅助上浮的拆除方法,利用SESAM软件对导管架与浮箱的上浮动态过程进行数值模拟,探究了压载水排放速率和波浪条件对上浮过程运动响应的影响,实现了大型导管架拆除上浮过程的连续动态模拟,研究结果可为国内外未来的大型导管架拆除提供参考。
1 计算理论
1.1 莫里森方程
1950年Morison等[10-12]基于绕流理论和相关实验等总结了一个半经验方程,即为莫里森方程。在该理论中,波浪力f被分为拖曳力fD和惯性力fI两部分,即:
(1)
式中:CD为拖曳力系数;ρ为流体密度;D为圆柱体直径;ux是垂直于圆柱体轴线的流体速度分量;CM为惯性力系数。工程经验表明,莫里森方程的计算结果较为精确,是小尺度结构波浪力计算的主要方程。
1.2 绕射理论
当结构物的尺度较大之时,Morison方程已不能用于计算波浪力,此时波浪受结构物的绕射效应必须计入,需要用到绕射理论来计算。绕射问题本质上是指入射波的波浪场与置于其中的静止结构之间的相互作用问题[13]。
入射波与散射波叠加达到稳定时将形成一个新的波动场,其速度势为Φ(x,y,z,t),可表示为
Φ(x,y,z,t)=ΦI(x,y,z,t)+ΦD(x,y,z,t)。
(2)
对于线性问题,Φ(x,y,z,t)可表示为
Φ(x,y,z,t)=φ(x,y,z,t)e-iωt=
[φI(x,y,z,t)+φD(x,y,z,t)]e-iωt。
(3)
线性入射波速度势可写为
(4)
式中:g为重力加速度;H为波高;ω为波浪角频率;k为波数;z为垂向坐标;d为水深;x为横坐标。
若得到波动场的速度势Φ后,代入到线性化的伯努利方程中,可得到波动场结构物表面上的波压强分布p:
(5)
最终可以得到作用在结构物上的波浪力和波浪力矩:
F=∬-pnds,
(6)
M=∬-p(r×n)ds。
(7)
1.3 时域运动方程
在环境荷载作用下,海洋浮式结构物的时域运动方程如下:


(8)

2 大型导管架浮箱辅助拆除方法
2.1 拆除过程
完整的大型导管架拆除过程为:(1)利用浮吊将浮箱从运输驳船中吊入水中;(2)在浮箱内加入一定压载水,调至设计浮态;(3)在牵引船的协助下,将浮箱安装在导管架4条主桩腿上;(4)浮箱进行适度排载,直至切割平面以上的导管架及浮箱总重量等于总浮力;(5)对导管架桩腿进行切割;(6)浮箱进行排载,使得每个时刻导管架和浮箱整体浮力大于重力,不断上浮;(7)压载水排放结束后,导管架和浮箱整体稳定在水面处;(8)在浮吊辅助和驳船拖拉作用下,完成起吊拖拉装船;(9)通过驳船将导管架拆除部分运输至岸上。
本文研究内容主要针对步骤(6)中的导管架和浮箱上浮过程的运动响应,并探究压载水排放速率和波浪条件对运动响应的影响,确定最优排水速率并避开不利波浪荷载,为实际工程提供一定的参考。
2.2 导管架拆除深度确定
本文研究的某大型深水导管架结构及其拆除部分主要参数如表1所示,其作业水深为213 m。根据国际公约规定,作业水深超过120 m的导管架,可采用部分切割的方式进行拆除,且高度须不小于55 m。考虑到整体拆除施工难度较大,而多次切割将导致成本增加,因此在第一次切割时以水面以下100 m处为切割平面,如图1所示。需要指出的是,本文仅对导管架切割后的上浮过程进行研究,不涉及其切割过程。

表1 导管架及其拆除部分的参数

图1 导管架拆除深度100 m示意图
2.3 “导管架-浮箱”整体模型
根据导管架的结构特点并参考Frigg油田DP2导管架拆除工程实例[14],采用钢制圆筒型浮箱作为辅助机构,浮箱的壁厚为30 mm,为了降低浮箱内压载水自由液面的影响,在其对称面上设有竖直舱壁。浮箱通过特种夹具刚性地连接在导管架桩腿上。图2为“导管架-浮箱”整体模型和舱室分布示意图。

图2 (a)“导管架-浮箱”整体模型图和(b)舱室分布示意图
导管架的拆除作业中,由于拆除部分过重,采用单一的浮吊方式会使装船作业难度较大。本文研究浮箱辅助导管架拆除的方法,在浮箱内压载水不断排放过程中,某一时刻下整体浮力略大于重力,“导管架-浮箱”整体会上浮一小段距离,由于压载水的减少和吃水的减小,重力和浮力均有所减小,但因排水过程的连续性,在这一过程中,整体的浮力一直略大于重力,因此由排水产生的上浮力会使“导管架-浮箱”整体不断上浮至水面。上浮过程的完成可以为后续装船做好铺垫作用,图3为导管架在浮箱辅助下的上浮过程示意图。

图3 “导管架-浮箱”整体上浮过程示意图
2.4 浮箱尺寸优选
在圆柱形浮箱模型的基础上,现对浮箱的尺寸(长度、底面半径)进行研究。由于“导管架-浮箱”整体结构在上浮过程中的稳性高(GM)会发生显著变化,需要对浮箱结构的尺寸进行详细的设计以避免整体结构在上浮过程中发生倾覆。图4为“导管架-浮箱”整体上浮开始前和上浮完成后的整体模型图,参数如表2所示,上浮高度为32.22 m。

图4 (a)上浮开始前示意图和(b)上浮完成后示意图

表2 两种典型吃水状态下“导管架-浮箱”整体模型参数
基于稳性理论中横稳性角和纵稳性角尽可能小的原则,筛选出浮箱相对最优尺寸。表3给出了不同浮箱尺寸下,海平面以上10 m六级风速(13.8 m/s)的条件下,利用HydroD软件计算得到“导管架-浮箱”整体上浮初始状态与压载水排空状态的横稳性和纵稳性结果,显然序号8、9对应的方案需进一步考虑(见表3)。
现按序号8、9对应的方案(见表3)选取上浮完成后的吃水状态,计算风倾力矩下整体结构横、纵方向的静稳性角和动稳性角,结果如表4所示,由结果可知序号9对应的静稳性角和动稳性角较小,对应的参数为相对最优化的尺寸选型方案。因此浮箱的长度和底面直径分别选取50和10 m。

表3 不同尺寸浮箱对应的“导管架-浮箱”整体稳性结果
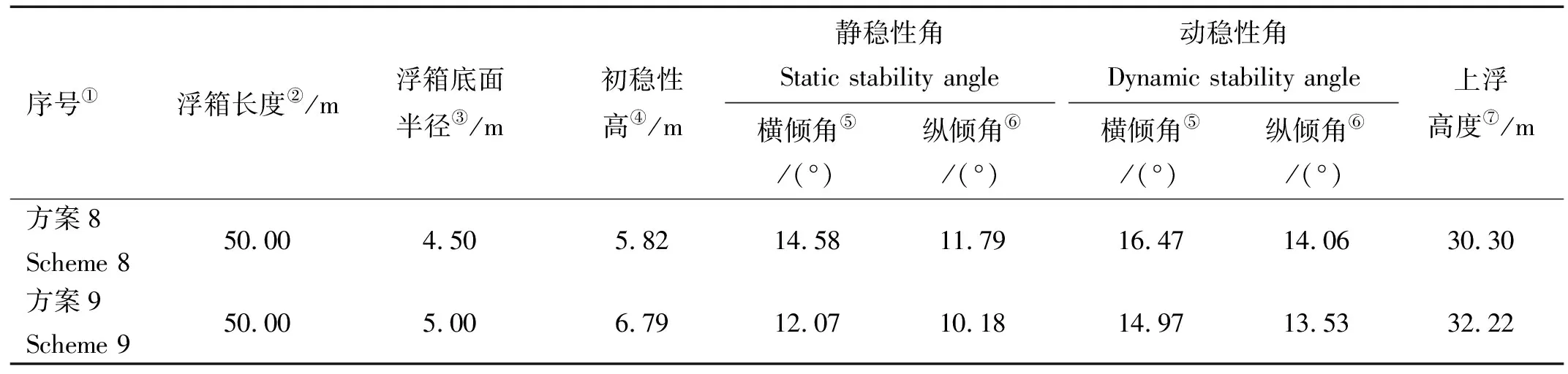
表4 进一步对比方案8与9的稳性结果
选取浮箱尺寸为长度50 m、底面直径10 m,进一步分析“导管架-浮箱”整体上浮过程中不同阶段吃水下的稳性结果,环境参数与上文相同,计算结果如表5所示。

表5 不同吃水下的“导管架-浮箱”整体稳性结果
在“导管架-浮箱”模型基础上,结合浮箱相对最优尺寸选型结果,利用HydroD软件,以稳性结果为依据,可以自动计算出导管架桩腿切割前各舱室最优压载方案,如表6所示。在数值模拟时,本研究通过质量点的质量变化来模拟压载水的排放,从而有效模拟了因压载水运动而产生的惯性力。

表6 导管架切割前各舱室压载水填充方案
3 “导管架-浮箱”上浮过程运动响应研究
3.1 坐标系规定
需要说明的是,本文波浪方向按照图5所示定义,图5(a)和(b)分别为主视图和俯视图。将导管架顶部横撑截面中心点在水面处的竖直投影点设为坐标原点,方向的范围为0°~360°。

图5 (a)主视图和(b)俯视图
3.2 频域运动分析
选取上浮结束后的吃水状态,通过HydroD软件的WADAM模块,基于势流理论,计算“导管架-浮箱”整体结构六自由度的运动响应传递函数,结果如图6所示。

图6 “导管架-浮箱”整体运动响应传递函数
由图6可知,纵摇、纵荡、垂荡频域运动响应曲线具有“单峰”的特点;而横摇、首摇、横荡频域运动响应曲线具有“多峰”的特点。具体来看,横摇峰值周期集中在5、10、17 s附近,纵摇和纵荡固有周期都在17 s左右,首摇峰值周期集中在6、7、12 s附近,横荡峰值周期集中在5、17 s附近,垂荡峰值周期在10 s左右,这意味着多个自由度之间存在耦合效应。同时可以发现,横摇、纵摇、首摇峰值一般不高于0.8°,这样的结果对于浮箱法拆除来说无疑是一个利好;但同时也需要关注纵荡与垂荡较大的峰值,特别是垂荡响应幅值,在8~10 s周期内出现了陡增。
在中国诸多海域中,周期为5~12 s的波浪较常见[15],因此在时域分析时应更多关注波浪周期为5~12 s时的“导管架-浮箱”整体运动轨迹,尤其要关注纵向和横向的偏移量,防止导管架发生碰撞事故。
3.3 压载水排放速率对运动响应的影响
浮箱内压载水不断排放,“导管架-浮箱”整体的浮力大于其重力,从而不断上浮。压载水排放越快,“导管架-浮箱”整体速度越大。受限于舱室水泵功率影响,排水时长显然不能过短。本文计算选取排水总时长范围为800~1 500 s,间隔100 s,对应排水速率范围为0.878~1.647 m3/s,工程中一般的水泵可满足要求[16]。波浪荷载选取JONSWAP谱,波浪周期10 s,波浪方向0°,波高1 m。通过SIMA软件实现了上浮过程的连续动态模拟,得到了不同排水速率下各自由度运动响应曲线,如图7所示。

图7 不同压载水排放时长下各自由度运动响应时域曲线
不难发现,在X方向上的位移,不同压载水排放时长对应的“导管架-浮箱”整体运动轨迹均呈现出不断偏移原位置向正方向运动的规律,在0~650 s左右,运动轨迹十分相似,而在650 s左右之后,偏移量最大值差异较大;在X方向上的转角变化规律均为:在0~650 s左右,“导管架-浮箱”整体在0°~0.5°之间小幅浮动,而在650 s左右之后,浮动幅度为2°~4°。
在Y方向上的位移,不同压载水排放时长对应的“导管架-浮箱”整体运动轨迹均呈现出不断偏移原位置向负方向运动的规律,在0~650 s左右,运动轨迹十分相似,且几乎不发生偏移,而在650 s左右之后,偏移量最大值差异较大;在Y方向上的转角变化规律均为:在0~650 s左右,“导管架-浮箱”整体在5°以内小幅浮动,而在650 s左右之后,浮动幅度会增大10°~15°。
在Z方向上的位移,不同压载水排放时长对应的“导管架-浮箱”整体运动规律是相似的,垂向重心运动轨迹为总体上升,伴随小幅度的上下往复运动;在Z方向上的转角变化规律均为:先从0°向180°进行“顺时针旋转”(从空中俯瞰角度下),再在150°~270°内往复转动,随着排水时间的增加,往复的次数也不断增加,排水时间为800 s时仅有一次,而排水时间为1 500 s时达到了4次,上浮过程呈现“螺旋式上升”的特点(见图8)。

图8 “导管架-浮箱”整体上浮过程呈现出“螺旋式上升”的特点
通过分析各方向运动规律可以发现,不同压载水排放时长下,上浮时间在650 s附近,“导管架-浮箱”在X和Y方向上的角速度会变大,经过大约10 s时间,X方向角速度从0.2(°)/s增加至1(°)/s,Y方向角速度从0.2(°)/s增加至3(°)/s,“导管架-浮箱”整体晃动幅度有所增加。

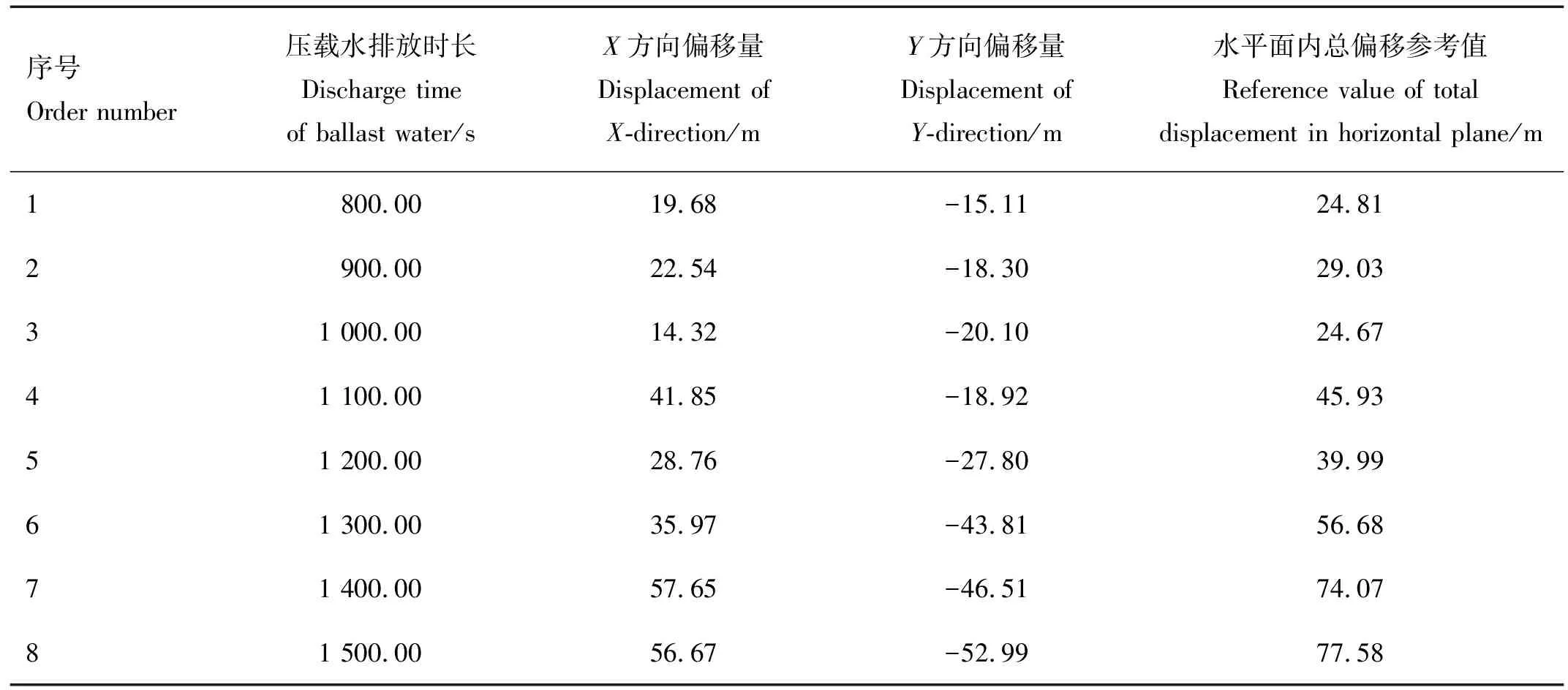
表7 各排水时长方案下最大偏移量
需要特别注意的是,SIMA软件里角度定义的范围是-180°~180°,定义方式如图9(a)所示;在SIMA软件中,对应整体坐标系下179°到181°的转变会出现突变现象,181°对应-179°(见图9(b))。为避免产生歧义,特作出解释。

图9 (a)SIMA软件角度定义示意图和(b)SIMA角度突变示意图
为进一步筛选最优压载水排放时长,现研究上浮过程垂向(Z方向)运动速率。图10为不同压载水排放时长下“导管架-浮箱”整体垂向运动速率曲线,表8为不同压载水排放时长下的垂向速率最大值。不难发现,排水时长为1 000 s时速度垂向速度峰值相对较小,峰值在0~0.7 m/s以内,且在1 000 s后速度很快就会稳定在0.01 m/s;而排水时长为800 s时速度峰值较大(0.792 m/s),对上浮过程不利。
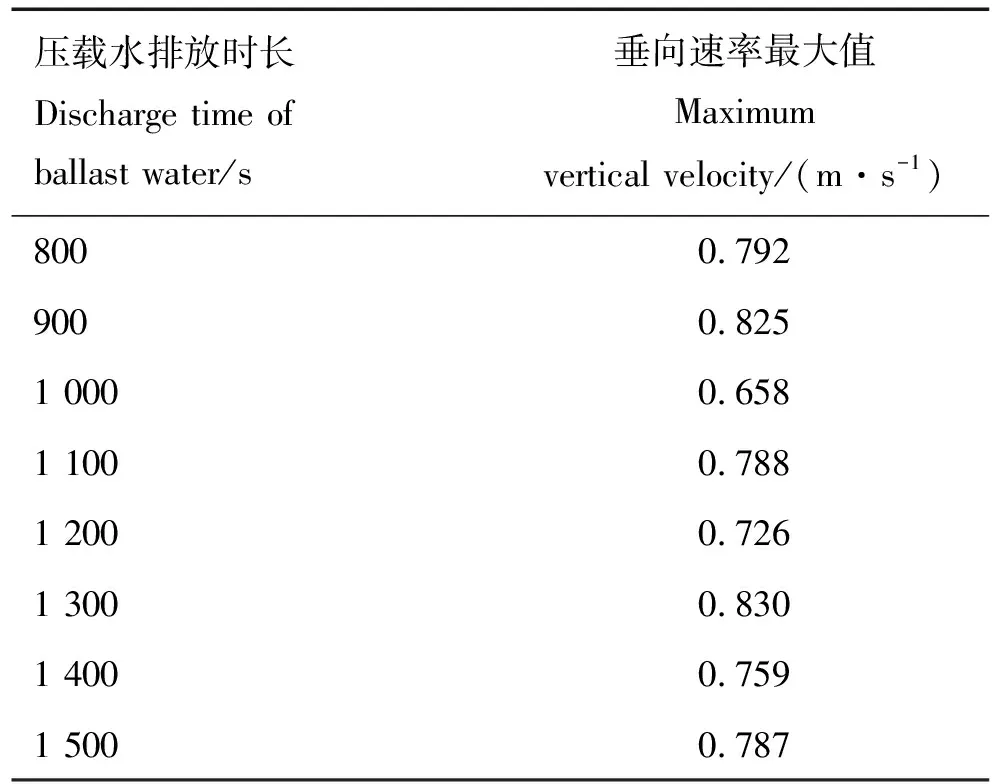
表8 不同压载水排放时长下的垂向速率最大值

图10 不同压载水排放时长下“导管架-浮箱”整体垂向运动速率
对比不同压载水排放时长下的“导管架-浮箱”各方向运动曲线和垂向运动速率曲线,综合考虑最大偏移量和运动速率,最终选取压载水排放时长为1 000 s作为最优方案。
3.4 波浪荷载对运动响应的影响
本节重点研究波浪荷载对“导管架-浮箱”结构整体上浮过程运动响应的影响。以参数敏感性分析为基本方法,探究波浪的周期、入射方向及波高对“导管架-浮箱”整体上浮过程运动响应的影响。本节以X和Y方向上重心偏移量最大值作为衡量标准。
根据3.3节频域分析结果可知,响应幅值峰值对应的周期多集中于3~18 s内,但常见波浪周期多集中于3~16 s内。因此,本节选取波浪周期计算范围为3~16 s,间隔为1 s,波高取1 m,重心偏移量最大值结果如表9所示。

表9 不同波浪周期下X和Y方向重心偏移量最大值
不难发现,在纵向(X方向)上的重心偏移量随波浪周期的变化而差异较大。其中,当波浪周期为4、13 s时X方向和Y方向的重心移动距离较大。因此通过分析波浪周期对“导管架-浮箱”整体上浮过程时域运动响应的影响,可以得出2个影响较大的周期:4、13 s,可将这2个周期值作为探究波浪入射方向和波高的影响时的典型波浪周期值进行计算,从上文中可知Z方向运动规律十分相似,因此不再对Z方向运动规律进行研究。X方向和Y方向偏移量最大值结果如表10所示。

表10 波浪周期4和13 s下各方向偏移量最大值
不难发现,当波浪周期为13 s,入射波方向为150°时,X方向的重心位移最大,为20.735 m,水平最大偏移量可达28.42 m;当波浪周期为4 s,入射波方向为150°时,Y方向的重心位移最大,为16.684 m,水平最大偏移量可达18.64 m。因此实际施工中应尽量避开以上2种情况。
4 结论
本文研究了基于浮箱辅助的导管架拆除上浮过程运动响应,建立了“导管架-浮箱”结构整体计算模型,根据稳性角进行了浮箱尺寸优化选型,探究了压载水排放总时长和波浪条件对“导管架-浮箱”整体运动响应的影响,实现了对“导管架-浮箱”上浮过程的动态模拟。主要结论如下:
(1)完成了浮箱尺寸的选型,选取浮箱长度50 m、半径5 m为优化后的尺寸,为“导管架-浮箱”整体上浮过程的研究提供了依据。
(2)研究了压载水排放速率对“导管架-浮箱”整体上浮运动响应的影响。当排放总时长为1 000 s时,“导管架-浮箱”整体在上浮过程中横向和纵向的重心位置移动量最小,在上浮过程中产生的偏移也较小,此时每个舱室排水速率为1.317 2 m3/s。
(3)研究了波浪荷载对“导管架-浮箱”整体上浮运动响应的影响,在波浪周期是4 s、入射方向为150°以及波浪周期13 s、入射方向150°的情况下,对上浮过程不利。水平总偏移最大值接近30 m,在实际工程中为保险起见,应当至少保证周围方圆50~60 m以内无障碍物,以免发生碰撞事故。

