疫情冲击下地方政府与中小型服务企业应对策略的演化博弈分析
单海燕 皮文杰 许吉俐
0 引言
2019年末的新冠疫情爆发至今,国内外疫情防控形势依旧严峻,防境外输入和疫情反弹的压力仍未消除.2022年以来,国内部分地区仍出现多点零星散发病例和局部聚集性疫情,如吉林、深圳、上海等地.现有研究表明,第三产业受疫情冲击的程度比第一、第二产业严重,部分服务产业营业额大幅下跌,其中中小型服务企业由于抗风险能力弱、生命周期较短等特征,受到的冲击尤为巨大[1].
现有关于本次疫情对我国中小型服务企业的影响研究结论较为一致.周新辉等[1]认为疫情在中短期内主要通过总需求链、企业生产链、供应链、销售链以及资金链和物流链等多重路径对我国中小服务型企业形成巨大冲击.陈诗一等[2指出疫情对小微企业的生产运营造成剧烈冲击,表现为生产成本高、经营绩效下降、市场信心不足.李刚等[3]从资金紧缺、原材料供应不足、消费需求动力不足等方面分析疫情背景下中小企业面临的生存困境.李涛等[4]以北京市为例,通过多情景设置模拟COVID-19疫情对北京经济发展的影响,研究表明新冠疫情在短期内使得北京经济下行压力增大,管控措施出台和需求萎缩进一步降低经济增速.
针对疫情给中小型企业带来的消极影响,各地方政府相继出台了一系列的政策.2020年,武汉市政府发布应对疫情支持中小企业经营发展的21条措施,在税费减免、金融支持、企业用工、既有政策执行等方面全力为企业营造更为宽松的发展环境;2021年,南京市政府出台《关于应对疫情影响支持企业稳定发展的若干举措》,聚焦“免、减、补、缓”,积极帮助企业应对疫情影响;2022年,吉林省制定了《吉林省进一步促进服务业恢复发展行动方案》,对承租国有房屋的服务业小微企业和个体工商户减免3个月租金,位于疫情中高风险地区的延长至6个月等.
为了应对本次疫情,部分学者相继从政府的角度提出了不同的扶持政策.Ashraf[5]研究发现政府检测和检疫政策以及针对企业和家庭的收入支持政策等在很大程度上给市场带来积极回报,而政府隔离公告给市场带来直接负面影响.朱武祥等[6]调研结果表明,受疫情影响中小微企业财务脆弱性风险较高,提出应提高税费政策落地效率,创新中小微企业金融服务模式等建议.林毅夫等[7]从中国发放消费券的具体特征出发,采用微信支付数据、疫情数据和城市经济状况数据估计消费券的发放效果,发现发放消费券对活跃交易、促进消费有积极效果.周新辉等[1]从财政、金融、产业等政策方面提出了一系列相应的宏微观风险防控对策.朱军等[8]构建动态随机一般均衡模型评估财政政策干预效果,发现政府财政干预能有效减缓中国经济下行压力,将增速下降10%降至下降5%.史丹等[9]认为应根据企业生存韧性和企业特征选取差异化帮扶政策,科学统筹推进常态化疫情防控和经济社会发展.
与此同时,部分学者从企业决策行为方面提出应对建议.吴晓波等[10]对疫情期间出现的6种商业模式研究发现,当合作关系存在不确定性时,企业利用共同专用互补性资产可以促进商业模式设计新颖性和效率性的提升.陈闻鹤等[11]基于马田系统和集对分析方法,构建企业疫情防控风险评估模型,能较好地处理疫情防控中的不确定性问题.赵雪芹等[12]研究发现我国企业复工复产政策存在轻需求型、企业要素上存在政策失衡等问题,应增加需求型政策工具运用比例以及增强政策工具与企业要素之间的协同效应.盛东方等[13]采用政策文本计算方法,探究突发公共事件下中小企业扶持政策供需匹配问题,发现金融支持类政策供需较为平衡,信息化征管和税费优惠类政策尚需加强舆论宣传,政务服务和物资保供类政策有待进一步增加政策供给.阳镇等[14]发现平台企业可以全新的组织载体、治理主体、治理过程和治理范式赋能新冠肺炎疫情防控和社会治理创新.李亚兵等[15]运用网络爬虫技术和专家加权打分法对零售企业商业模式创新风险进行评估,发现线上零售、直播、短视频和社群营销模式受疫情的影响发展最为迅速,在疫情趋于常态化后关注度仍在增加.
部分学者运用演化博弈模型分析疫情冲击下不同利益相关方的决策行为.冯兰萍等[16]构建“政府-网民-关键节点”三方演化模型,探究突发事件网络舆情政府干预时机和应对措施.谢地等[17]从政治经济学视角,发现面对重大突发公共卫生事件的冲击,中央政府、地方政府及其民众之间存在复杂的博弈.朱立龙等[18]构建“药品生产企业-第三方药品检测机构-政府监管部门”之间的三方演化博弈模型,探讨政府奖惩机制下药品安全质量监管机制.
通过对现有文献的梳理发现,相关研究主要侧重于新冠疫情对企业造成的消极影响或可能存在的潜在机遇,政府及企业应采取的扶持政策或应对策略等.现有研究认为政府应对企业进行必要的扶持,但针对扶持的力度研究甚少;消费券作为特殊时期推动经济复苏的一种重要手段,消费券的实际抵扣力度将影响到消费者的消费行为,这方面研究亦甚少涉及.
从世界历史经验看,消费券作为拉动消费的一种形式,是许多国家特殊时期的特殊办法,是遏制经济下滑、刺激消费、推动经济复苏的重要手段之一[19].2020年3月,国家发展改革委员会等23个部门联合印发了《关于促进消费扩容提质加快形成强大国内市场的实施意见》,提出大力优化国内市场供给,持续提升居民消费能力、全面营造放心消费环境的一系列政策措施.随后,南京、杭州、广西等地区率先与相关互联网平台合作,积极探索消费券使用模式与政策.2022年3月,香港特区政府为促进本地消费,向全港市民派发首轮消费券约664亿元,且消费券的涵盖范围很广,除本地零售业和服务业,亦包括实体和网上店铺.2020年6月,中国社会科学院金融研究所发布《数字消费券助力中国经济“疫后”重建》研究报告,报告指出我国各地政府发行的数字消费券具有“见效快”、“杠杆高”等明显优势.
然而,疫情防控期间,地方政府财政大幅度增支减收,消费券的发放会给地方财政造成一定压力.那么,地方政府是否应对不同自救模式下的中小型服务企业区别实施扶持政策,政府区别化的扶持方式和力度是否会影响中小型服务企业的自救方式,企业是否愿意以疫后重建为契机改变现有服务模式,政府扶持政策、企业自救方式、消费券的实际抵扣力度等如何影响消费者的消费行为,是否存在适当的条件能实现地方政府、中小型服务企业良性合作,真正刺激消费,让利于民?基于此,本文以地方政府和中小型服务企业联合发行消费券应对疫情为前提,构建地方政府、中小型服务企业和消费者的三方演化博弈模型,研究政府有偿、无偿扶持策略,企业消极、积极自救行为,消费者持券、自主消费模式间的相互影响作用,以期借助实施差异化的扶持政策与精准发放消费券,真正实现疫后经济复苏.
1 模型构建
1.1 博弈主体及策略
选择疫情冲击下与中小型服务企业日常运营关联度较高的主要利益相关者:地方政府、中小型服务企业以及消费者,且每类主体均只具有有限理性.
1)地方政府行为策略
假设地方政府(以下简称“政府”)在博弈中出现两种行为:①无偿扶持:政府对中小型服务企业(以下简称“企业”)进行无偿支持,如无条件地对国有土地的租金进行适当减免、给予贷款企业贴息支持、延缓缴纳税款等行为,以帮助企业渡过难关;②有偿扶持:政府对满足一定条件的企业给予经济和政策扶持,如对不裁员或少裁员、积极自救的企业,可获得政府奖励、返还所得税及增值税等,以兼顾企业和员工的利益.因此,假设政府行为策略空间为SG={无偿扶持,有偿扶持},政府分别以x和1-x的概率选择无偿扶持和有偿扶持策略.
2)中小型服务企业行为策略
假设中小型服务企业在博弈中出现两种行为:①积极自救:企业不通过裁员或缩减业务应对疫情冲击,而是加快数字化转型积极改变现有服务模式,如发展数字化社群服务、微创新、线上经营、线上协同办公等业务,以实现自救;②消极自救:企业认为疫情已给自身造成极大冲击,没有更多资金或能力支持其转型,企业仅专注主营业务,一方面选择裁员或缩减非主营业务等方式减少企业开支,另一方面依靠政府政策支持产生“搭便车”红利,例如参与消费券的发放与使用,以实现自救.因此,假设企业行为策略空间为SE={积极自救,消极自救},企业分别以y和1-y的概率选择积极自救和消极自救策略.
3)消费者行为策略
假设消费者在博弈中会出现两种行为:①持券消费:由于无门槛消费券的存在,或者对于有门槛消费券,消费达到既定消费金额,消费者愿意选择持券消费享受政策红利;②自主消费:由于有些消费券的获取途径相对繁琐、使用门槛较高、使用期限约束等,难以惠及诸如缺乏移动支付经验、消费需求相对较低的用户群体,该部分消费者选择自主消费.因此,假设消费者行为策略空间为SC={持券消费,自主消费},消费者分别以z和1-z的概率选择持券消费和自主消费策略.
1.2 模型假设
1.2.1 变量及收益假设
1)假设政府选择无偿扶持策略时,政府对消极自救、积极自救企业的补贴额均为Sf;政府选择有偿扶持策略时,因其鼓励企业积极自救,对消极自救、积极自救企业的补贴额分别为Sp,μSp,其中μ为企业积极自救策略对政府有偿补贴的影响因子且μ>1;政府对企业不论进行无偿扶持还是有偿扶持,均可提升政府的公信力,但择优补贴更可激励企业创新,增强内生发展动力,从而更能提升政府公信力.因此,假设政府选择无偿扶持、有偿扶持策略时,政府公信力的提升值分别为G,ηG,其中η为政府有偿扶持策略对公信力的影响因子且η>1.
2)假设企业选择积极自救策略,在未来一段时间可提升企业的发展潜力D,少裁员或不裁员有助于提升员工的凝聚力,企业获得的无形收益为I,但积极自救需投入成本Ct,亦需承担更多员工工资福利等费用Cs;企业若选择消极自救,其在发展潜力、无形收益上均低于积极自救时,其投入的自救成本亦相对较低,但应承担诸如裁员所补偿员工的费用Cr.因此,企业积极自救和消极自救下的收益分别表示为Pa-Cs,σPa-Cr,其中Pa=D+I-Ct,σ为消极自救策略对企业收益的影响因子且0<σ<1.
3)假设政府和企业为刺激消费,可独立或联合发行消费券,消费券使用后才产生成本或带来收益.由于政府给予积极自救的企业更多补贴,以及积极自救企业更愿意让利于民以吸引消费者.因此,假设企业消极自救、积极自救时消费券的实际抵扣金额分别为Cv,βCv,其中β为企业积极自救策略对消费券抵扣金额的影响因子且β>1.
4)政府和企业联合发行消费券时,政府和企业承担的比例分别为λ和1-λ;不论消费者是否使用消费券,企业可从其消费中直接获得营业收入,而政府亦可间接地获得税收带来的财政收入,其中政府和企业所获消费收益的比例分别为δ和1-δ.
5)假设企业采用积极自救策略比消极自救时给消费者提供更加优质的服务,因此设消费者在企业消极自救、积极自救下获得的服务价值分别为S,αS,其中α为积极自救策略对消费者服务价值的影响因子且α>1;设消费者在自主消费中实际消费为V,由于发放消费券的目的为刺激消费,因此假设消费者若使用消费券,其实际消费金额γV应高于自主消费时,其中γ为消费券对实际消费额的影响因子且γ>1.
1.2.2 变量大小假设
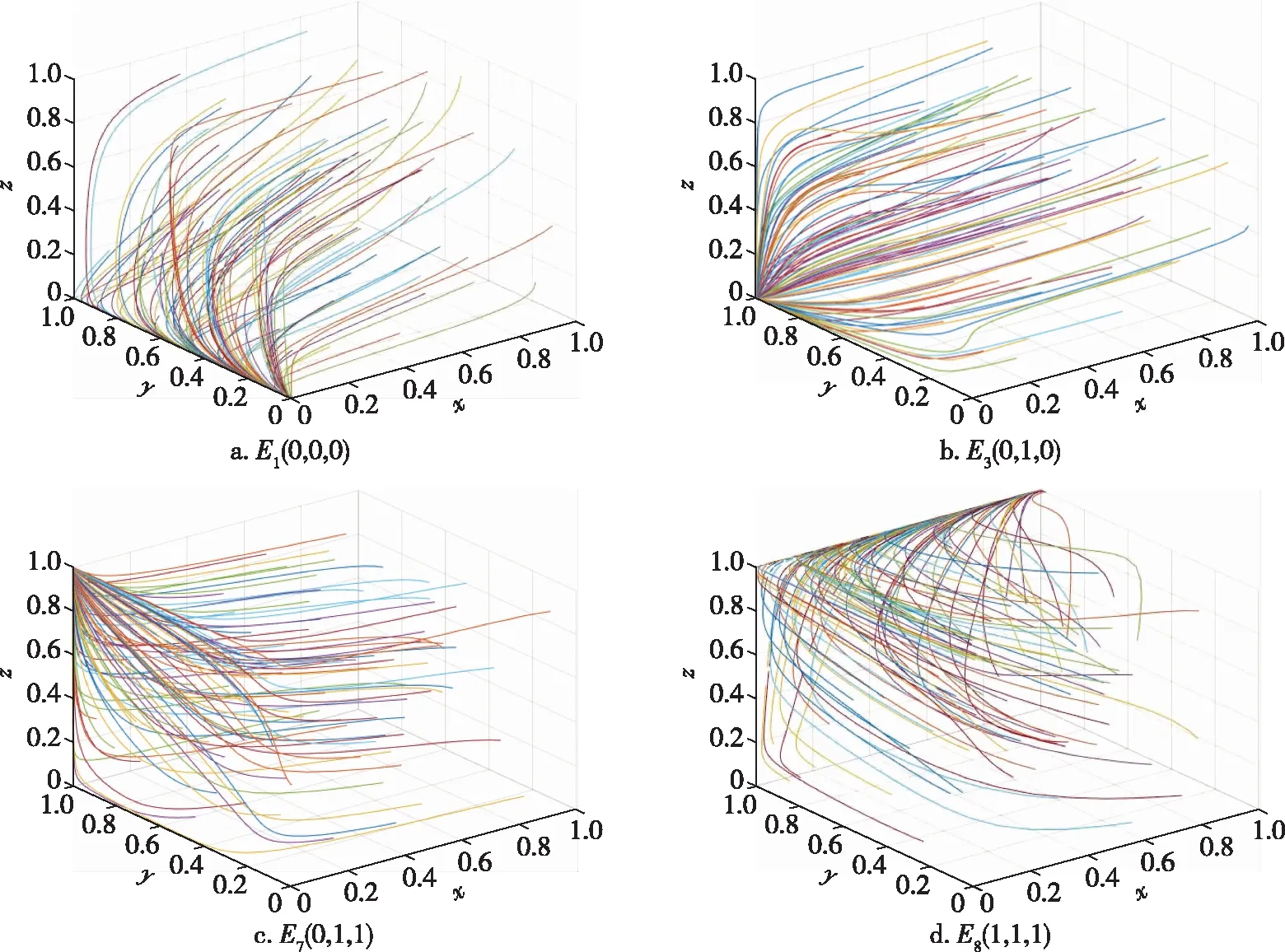
1)假设企业在不考虑政府补贴情形时,企业选择裁员的成本低于不裁员时承担被裁员员工工资福利等费用,即Cr 2)结合现实实际,在消费券发放过程中,政府承担了大部分,即设0.5<λ<1.由于税收仅占企业营业收入的一小部分,所以企业从消费者消费中获得的直接收益大于政府的间接收益,即设0<δ<0.5. 本文构建的模型中涉及到的相关变量符号及解释如表1所示. 根据上述模型假设,构建地方政府、中小型服务企业和消费者三方演化博弈的收益矩阵,每个得益数组分别表示政府、企业及消费者的收益,如表2所示. 假设政府选择无偿扶持策略时获得的期望收益πG1为 πG1=y(z(G+δV-Sf)+ (1-z)(G+δγV-Sf-λβCv))+ (1-y)(z(G+δV-Sf)+(1-z)· (G+δγV-Sf-λCv))=G-Sf+δVz+δγV(1-z)- λCv(1-z)(1-y+yβ). 政府选择有偿扶持策略时获得的期望收益πG2为 πG2=y(z(ηG+δV-μSp)+ (1-z)(ηG+δγV-μSp-λβCv))+ (1-y)(z(ηG+δV-Sp)+(1-z)· (ηG+δγV-Sp-λCv))=ηG-Sp+δVz+δγV(1-z)- (μ-1)Spy-λCv(1-z)(1-y+yβ). 表1 主要参数符号及解释 注:Cr 政府的复制动态方程可表示为 x(1-x)((μ-1)Spy+Sp-Sf- (η-1)G). (1) 类似地,使用πE1与πE2分别表示企业选择积极自救与消极自救策略的期望收益.πE1与πE2分别表示如下: 表2 三方演化博弈收益矩阵 πE1=x(z(Sf+(1-δ)V+Pa-Cs)+ (1-z)(Sf+(1-δ)γV+Pa-Cs-(1-λ)βCv))+ (1-x)(z(μSp+(1-δ)V+Pa-Cs)+ (1-z)(μSp+(1-δ)γV+Pa-Cs-(1-λ)βCv))= Pa-Cs+μSp+(1-δ)γV+(Sf-μSp)x+ (1-γ-δ+δγ)Vz-(1-λ)(1-z)βCv, πE2=x(z(Sf+(1-δ)V+σPa-Cr)+ (1-z)(Sf+(1-δ)γV+σPa-Cr-(1-λ)Cv))+ (1-x)(z(Sp+(1-δ)V+σPa-Cr)+ (1-z)(Sp+(1-δ)γV+σPa-Cr-(1-λ)Cv))= σPa-Cr+Sp+(1-δ)γV+(Sf-Sp)x+ (1-γ-δ+δγ)Vz-(1-λ)(1-z)Cv. 因此,企业的复制动态方程为 y(1-y)((μ-1)Sp(1-x)- (1-λ)(β-1)Cv(1-z)+ (1-σ)Pa+Cr-Cs). (2) πC1与πC2分别表示消费者选择自主消费和持券消费策略的期望收益,πC1与πC2可以表示为 πC1=x(y(αS-V)+(1-y)(S-V))+ (1-x)(y(αS-V)+(1-y)(S-V))= αSy-Sy+S-V, πC2=x(y(αS+βCv-γV)+(1-y)(S+Cv-γV))+ (1-x)(y(αS+βCv-γV)+(1-y)(S+Cv-γV))= αSy-Sy+βCvy-Cvy+S+Cv-γV. 因此,消费者的复制动态方程为 z(1-z)(-(β-1)Cvy-Cv+(γ-1)V). (3) 由于政府、企业以及消费者的有限理性,各博弈方在一次决策中很难做出最佳的策略选择.因此,方程(1)、(2)和(3)可视为一个演化过程,形成一个复制动态系统,如(4)式所示,方程组(4)的解即为该动力系统的均衡解. (4) 其中 f1(y,z)=(μ-1)Spy+Sp-Sf-(η-1)G, f2(x,z)=(μ-1)Sp(1-x)- (1-λ)(β-1)Cv(1-z)+ (1-σ)Pa+Cr-Cs, f3(x,y)=-(β-1)Cvy-Cv+(γ-1)V. 该三维动力系统存在8个纯策略均衡点,即E1(0,0,0),E2(1,0,0),E3(0,1,0),E4(0,0,1),E5(1, 1,0),E6(1,0,1),E7(0,1,1)与E8(1,1,1).所有博弈方在每个均衡点上都采取纯策略,这些均衡点构成了解域Ω的边界. 在得到系统均衡点之后,需分析它们的渐近稳定性.根据Selten[20]与Ritzberger等[21]的研究可知,均衡点当且仅当是严格纳什均衡和纯策略纳什均衡时才能被称为演化稳定策略(ESS).8个纯策略纳什均衡点的渐近稳定性可通过计算Jacobian矩阵的特征值来获得[22].雅克比矩阵[23]表示如下: (5) 其中 H11=(1-2x)((μ-1)Spy+Sp-Sf-(η-1)G), H12=x(1-x)(μ-1)Sp, H13=0, H21=y(1-y)(-(μ-1)Sp), H22=(1-2y)((μ-1)Sp(1-x)- (1-λ)(β-1)Cv(1-z)+(1-σ)Pa+Cr-Cs), H23=y(1-y)(1-λ)(β-1)Cv, H31=0,H32=z(1-z)(-(β-1)Cv), H33=(1-2z)(-(β-1)Cvy-Cv+(γ-1)V). 将各个纯策略均衡点代入雅克比矩阵,分别得到3个特征值,并根据各均衡点的特征值实部符号判定是否为演化稳定策略,均衡点为演化稳定策略的条件如表3所示. 根据以上分析,在政府、企业和消费者三方演化博弈时,系统的稳定性策略受许多参数影响.为更直观地展示三方策略选择的动态演化过程,本文采用数值仿真分析,根据实际情况和参数的逻辑关系,部分参数设置[24]如下:μ=1.4,σ=0.8,β=1.8,γ=1.5,λ=0.7,在满足不同参数条件下模拟E1(0,0,0),E3(0,1,0),E7(0,1,1),E8(1,1,1)的演化路径,如图1所示. 表3 各均衡点在雅克比矩阵的特征值及稳定性判断 1)在上述参数取值不变的情况下,令Sf=20,Sp=10,G=5,D=2,I=0.5,Ct=4,Cs=2,Cr=1,Cv=5,V=7,η=1.5,此时满足表3中E1(0,0,0)稳定性条件,演化结果如图1a所示,政府、企业和消费者最终分别稳定到“有偿扶持”、“消极自救”和“持券消费”策略,即三群体的演化稳定策略为E1(0,0,0).当参数满足E1(0,0,0)稳定性条件时,由于(γ-1)V 2)在上述参数取值不变的情况下,Sf=20,Sp=1,G=8,D=2,I=1.5,Ct=1,Cs=1.5,Cr=1,Cv=8,V=11,η=1.5,此时满足表3中E3(0,1,0)稳定性条件,演化结果如图1b所示,政府、企业和消费者最终分别稳定到“有偿扶持”、“积极自救”和“持券消费”策略,即三群体的演化稳定策略为E3(0,1,0).当参数满足E3(0,1,0)稳定性条件时,由于μSp-Sf<(η-1)G,有G-Sf<ηG-μSp<ηG-Sp,表明不论其他博弈方采用何种策略,政府选择无偿扶持时的收益小于有偿扶持时的收益,此时政府应选择“有偿扶持”策略;若政府选择“有偿扶持”,由于(μ-1)·Sp+Cr-Cs>(1-λ)(β-1)Cv-(1-σ)Pa,整理后发现无论消费者选择何种策略,企业选择消极自救时的收益小于积极自救时,企业应选择“积极自救”;若政府选择“有偿扶持”、企业选择“积极自救”,由于(γ-1)V<βCv,即γV-βCv 3)在上述参数取值不变的情况下,令Sf=2,Sp=1,G=0.5,D=0.2,I=0.05,Ct=0.5,Cs=0.2,Cr=0.1,Cv=0.2,V=1.3,η=1.5,此时满足表3中E7(0,1,1)的稳定性条件,演化结果如图1c所示,政府、企业和消费者最终分别稳定到“有偿扶持”、“积极自救”和“自主消费”策略,即三群体的演化稳定策略是E7(0,1,1).当参数满足E7(0,1,1)稳定性条件时,由于βCv<(γ-1)V,易见V<γV-βCv<γV-Cv,表明不论其他博弈方采用何种策略,消费者选择自主消费时的消费额低于其选择持券消费时,此时,消费者应选择“自主消费”策略;若消费者选择“自主消费”,由于G-Sf<ηG-μSp,有G-Sf<ηG-μSp<ηG-Sp,表明不论企业如何选择,政府选择无偿扶持时的收益低于有偿扶持时,因此政府应选择“有偿扶持”;若消费者选择“自主消费”、政府选择“有偿扶持”,由于(μ-1)Sp+(1-σ)Pa>Cs-Cr,表明企业选择消极自救时的收益小于积极自救时,企业应当选择“积极自救”.因此,政府、企业和消费者最终分别稳定到“有偿扶持”、“积极自救”和“自主消费”策略. 图1 各方演化路径Fig.1 Evolution paths of each stakeholder 4)在上述参数取值不变的情况下,令Sf=2,Sp=6.5,G=1,D=5,I=4,Ct=1,Cs=3,Cr=1.5,Cv=1,V=4.5,η=1.4,此时满足表3中E8(1,1,1)的稳定性条件,演化结果如图1d所示,政府、企业和消费者最终分别稳定到“无偿扶持”、“积极自救”和“自主消费”策略,即三群体的演化稳定策略是E8(1,1,1).当参数满足E8(1,1,1)稳定性条件时,由于βCv<(γ-1)V,易见V<γV-βCv<γV-Cv,表明不论其他博弈方采用何种策略,消费者选择自主消费时的净消费额低于其选择持券消费时,因此消费者应选择“自主消费”策略;若消费者选择“自主消费”,由于Cs-Cr<(1-σ)Pa,整理后可发现无论政府选择何种策略,企业选择消极自救时的收益小于积极自救时,此时企业应选择“积极自救”;若消费者选择“自主消费”、企业选择“积极自救”,由于ηG-μSp 1)积极自救策略对有偿补贴的影响因子μ 以点E8(1,1,1)为例进行分析,在其他参数取值不变的情况下,将企业积极自救策略对政府有偿补贴的影响因子μ分别设置为1.2、1.4、1.6,政府行为策略的演化路径如图2a所示. 由图2a可知:当有偿补贴的影响因子μ较小时,政府选择无偿扶持的概率趋于0,此时政府对企业有偿扶持的付出相对较少,政府趋于选择有偿扶持而不是无偿扶持;随着有偿补贴的影响因子μ逐渐增大,有偿扶持所承担的费用逐渐增多,政府的策略选择发生转变,政府更愿意选择无偿扶持,且有偿补贴的影响因子μ的值越大,收敛到1的速度加快,即政府趋于选择无偿扶持. 2)有偿扶持策略对公信力的影响因子η 以点E8(1,1,1)为例进行分析,在其他参数取值不变的情况下,将政府有偿扶持策略对公信力的影响因子η分别设置为1.1、1.5、1.8,政府行为策略的演化路径如图2b所示. 从图2b可知:当公信力的影响因子η较小时,政府选择无偿扶持策略的概率趋于1,即较低的公信力很难刺激政府选择有偿扶持,政府趋于选择无偿扶持策略;但随着公信力的影响因子η逐渐提升,政府选择无偿扶持的概率逐渐由1转为0,即政府趋于选择有偿扶持以提升公信力. 1)积极自救策略对有偿补贴的影响因子μ 以点E3(0,1,0)为例进行分析,在其他参数取值不变的情况下,将企业积极自救策略对政府有偿补贴的影响因子μ分别设置为1.2、1.4、1.6,企业行为策略的演化路径如图3a所示. 从图3a可见,不管企业积极自救策略对政府有偿补贴的影响因子μ取值如何变化,企业最终将选择积极自救策略,即政府给予积极自救企业有偿补贴力度的不同不会影响企业是否选择积极自救策略,但随着μ的增加,收敛于积极自救策略的速度变快,即政府给予积极自救企业的有偿补贴越高,企业趋于快速选择积极自救策略.总的来说,有偿补贴值不会影响企业积极自救策略的选择,但是在一定限度内,适当地提升补贴力度可以促进企业加快选择积极自救以应对疫情冲击. 图2 相关参数对政府演化稳定策略的影响Fig.2 Influence of relevant parameters on government’s evolutionary stability strategy 图3 相关参数对企业演化稳定策略的影响Fig.3 Influence of relevant parameters on enterprise’s evolutionary stability strategy 2)积极自救策略对消费券抵扣金额的影响因子β 以点E1(0,0,0)为例进行分析,在其他参数取值不变的情况下,将企业积极自救策略对消费券抵扣金额的影响因子β分别设置为1.4、1.6、1.8,企业行为策略的演化路径如图3b所示. 从图3b可知,不论消费券抵扣金额的影响因子β取值的变化,企业最终选择积极自救策略的概率趋于0,即当积极自救策略使得企业需要增加消费券抵扣额从而导致自身收益降低时,企业更趋于选择消极自救,且随着β的增加,收敛于消极自救的速度加快,说明在没有额外的经济扶持情况下,企业不愿意选择积极自救,让利于消费者.因此,政府在一定程度上应给予积极自救企业提供适当补贴,以应对疫情冲击. 图4 相关参数对消费者演化稳定策略的影响Fig.4 Influence of relevant parameters on consumer’s evolutionary stability strategy 1)消费券对实际消费额的影响因子γ 以点E7(0,1,1)为例进行分析,在其他参数取值不变的情况下,将消费券对实际消费额的影响因子γ分别设置为1.4、1.6、1.8,消费者行为策略的演化路径如图4a所示. 从图4a可知:不论消费券对实际消费额的影响因子γ取值如何变化,消费者最终趋于选择自主消费策略,由于若使用消费券导致消费者实际消费值过高,即额外花费过大,相比之下,消费者不愿持券消费,从而选择收益相对较高的自主消费策略;且消费券对实际消费额的影响因子γ越大,消费者选择自主消费的速度加快,即一旦使用消费券所花费的额外支出越多,消费者越趋于选择自主消费.因此,为了使消费者愿意选择持券消费,一方面需要减小消费券对实际消费额的影响,另一方面需要政府和企业的通力合作,让消费券能真正发挥作用. 2)积极自救策略对消费券抵扣金额的影响因子β 以点E3(0,1,0)为例进行分析,在其他参数取值不变的情况下,将企业积极自救策略对政府有偿补贴的影响因子β分别设置为1.1、1.5、1.9,消费者行为策略的演化路径如图4b所示. 从图4b可知:不论企业积极自救策略对消费券抵扣金额的影响因子β取值如何变化,消费者最终趋于选择持券消费策略,即在积极自救企业的进一步补贴之下,消费者认为持券消费的收益大于自主消费,更愿意选择持券消费;且企业积极自救策略对消费券抵扣金额的影响因子β越大,消费者选择持券消费速度加快,即积极自救企业让利越多,消费者越愿意选择持券消费.因此,企业可在一定范围内提高对消费券的抵扣金额,刺激消费者持券消费,以获取更多利润. 中小型服务企业由于抗风险能力弱、生命周期较短等弱势特征,在此次疫情中容易受到巨大冲击,中小型服务企业面临严峻压力的同时也处于发展的关键期,在应对疫情的同时寻求发展突破是中小型服务企业面临的核心难题.本文以地方政府和中小型服务企业联合发行消费券应对疫情为前提,构建政府、企业和消费者的三方演化博弈模型,探讨系统内各利益相关方的演化稳定策略和稳定性条件,通过数值仿真分析企业自救策略对政府补贴行为的影响、消费券抵扣金额对企业自救方式的影响以及企业自救力度对消费者消费模式的影响等.研究结果表明: 1)政府有偿扶持策略下补贴额较低、有偿扶持策略对公信力的影响较大,将促使政府选择对企业进行有偿扶持;企业积极自救策略下所获有偿补贴较高、对消费券抵扣金额较少,企业越愿意坚持积极自救策略;消费券对消费者实际消费额的影响程度较小、积极自救企业对消费券抵扣金额较多,将促使消费者选择持券消费. 2)政府对积极自救企业的补贴存在阈值,政府有偿扶持所承担的费用逐渐增多,政府将从有偿扶持策略逐渐转变为无偿扶持策略;政府给予积极自救企业有偿补贴值不会影响企业积极自救策略的选择,但是在一定限度内,适当地提升补贴强度可以促进企业加快选择积极自救以应对疫情冲击. 3)由于在没有额外的经济扶持情况下,企业不愿意选择积极自救,让利于消费者,因此政府对积极自救的企业应提供额外补贴,使得企业让利于消费者的成本相对减小,从而促使企业积极自救,同时让利于消费者以刺激消费.因此,实施差异化的扶持政策、结合消费券精准发放,可促进经济复苏.1.3 模型中使用的符号及解释
1.4 收益矩阵
2 演化博弈模型分析
2.1 复制动态方程


2.2 均衡点及稳定性分析
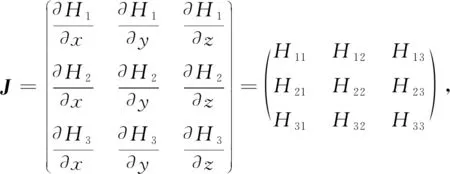
3 数值仿真

4 参数分析
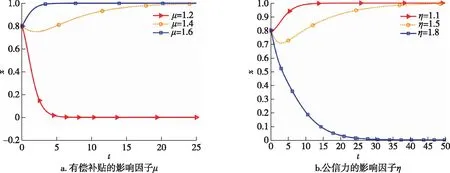
4.1 相关参数对政府行为的影响
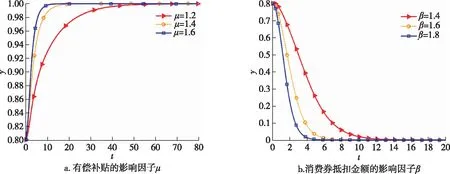
4.2 相关参数对企业行为的影响
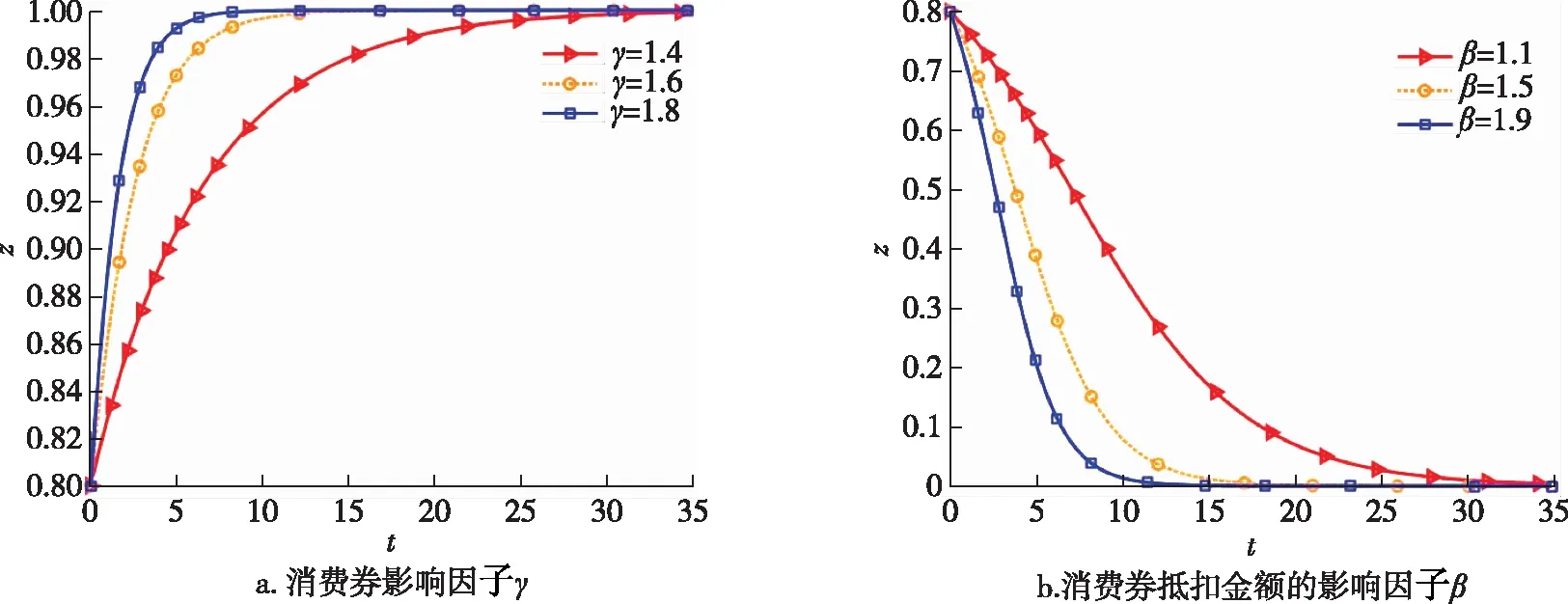
4.3 相关参数对消费者行为的影响
5 结束语

