海狸色獭兔21 日龄窝重（泌乳力）校正公式的制订与应用

牛晓艳，李燕平，郑建婷，詹海杰，唐耀平，任克良

（山西农业大学 动物科学学院，山西 晋中 030801）

21 日龄窝重（泌乳力）是养兔育种和生产中反映母兔繁殖性能的一个重要指标，而且泌乳力与母兔的其他繁殖性能指标也表现出较强的正相关关系［1-3］，对种兔选育具有重要意义。在规模化养兔生产中，根据养殖场使用的饲料配方和营养水平，常采用42 d 或49 d 作为一个周期的繁殖模式，这2 种模式的仔兔断奶日龄均采纳35 d［4-6］，但多数养殖场的补饲往往在仔兔出生后18～20 日龄开始，以满足母兔泌乳高峰后乳汁营养水平下降而仔兔快速生长对营养的需求［7-10］。因此，21 日龄后的仔兔窝重受饲料营养水平影响较大，不能准确反映母兔的泌乳水平，而21 日龄的窝重则准确的反映了母兔泌乳力。

生产实践中，由于母兔同期发情、同期配种以及同期生产技术尚不完善，且规模较小的兔场采用自然交配进行繁育的情况较多，对母兔的发情日期不加控制，导致仔兔出生时间不集中，给繁殖性能的测定造成一定困难，也会干扰后续育种方案制订过程中各参数计算的准确性。基于泌乳力在家兔繁育中的重要作用，对该指标的校正具有较大意义。本研究以海狸色獭兔仔兔为研究对象，连续收集其18～23 日龄的窝重数据，参考国外文献中报道的猪种21 日龄窝重的校正公式，制订出符合生产实际的海狸色獭兔母兔泌乳力的校正公式，以指导生产实践。

1 材料与方法

1.1 试验动物

选择山西农业大学（省农业科学院）畜牧兽医研究所实验兔场的繁殖母兔作为试验动物，所选母兔均为体重（1759±293.5）g 和体尺（35.8±1.29）cm 相近、且与仔兔同笼饲养的初产母兔，于2021 年5-6 月对50 窝初生仔兔进行18～23 日龄窝重的测量。其中，各日龄窝重在仔兔出生后18～23 d 早9：00-10：00 采用电子秤进行测定，精度为5 g。试验过程中所有母兔的饲料配方和管理方式相同，自由饮水。

1.2 试验方法

1.2.1 窝重数据的预处理

在收集的窝重数据中，首先剔除耳号标记不清和无号母兔的产仔数据；剔除产仔数≤2 和≥9的母兔产仔数据。

1.2.2 窝重校正模型的形式

参考美国养猪协会21 日龄窝重的校正公式［11］：

校正21日龄窝重=21日龄实际窝重(a-b×日龄+c×日龄2) +d×带仔数+f×哺乳天数+e（e 为残差）

由于在养兔生产中哺乳天数和日龄为相同的指标，上式可简化为：

校正21日龄窝重=21日龄实际窝重(a-b×日龄+c×日龄2) +d×带仔数+e

从上述公式中可以看出，公式为二元二次方程，其中a，b，c，d为公式中各变量的系数，需要进行估计。

1.2.3 窝重校正模型的拟合和参数估计

建立数据集后，采用R（3.2.4 版）中的lm 函数分别以日龄和带仔数为自变量（x1和x2），窝重为因变量（y）进行二元一次和二元二次方程的拟合分析；用summary 函数估计各拟合方程参数；用anova 函数和AIC 函数比较和选择最优模型［12-13］。

1.2.4 拟合效果评估

(三)科学评价试卷的区分功能，合理调控难度.高考的主要功能是区分考生，为高校录取提供有效的高考分数.因此其区分能力应是评价试卷质量最重要指标.标准差和变异系数应该给予更多的关注.难度只是评价试卷的一个指标，而且对高考而言并不是十分重要的，但因为其牵涉考生的得分情况、考生的心理感受以及各省录取的分数线，因此受到了超乎寻常的关注.从本文的分析可以看出，试卷只要不是过易或过难，其对考生的区分精细、明确，就是可接受的范围.因此高考应该根据区分和选拔的主体任务，合理调控试卷的难度，使试卷更好地发挥区分功能和对中学教学的导向作用.

拟合方程确定后，采用R（3.2.4 版）中的plot函数绘制模型的回归诊断图，同时采用21 日龄测定的真实窝重数据与模型拟合值进行比较，计算拟合度R2。

1.2.5 21 日龄校正模型的制订

以21 日龄时窝重值y21为标准，可进一步推导出校正模型公式和各测定日龄与不同带仔数下的校正系数。

2 结果与分析

2.1 各日龄窝重的描述性统计量

将异常数据和极端值剔除后，海狸色獭兔18～23 日龄窝重的描述性统计量如表1 所示。由表1 可见，18～23 日龄海狸色獭兔平均窝重呈逐渐上升的趋势，标准差随平均数的增加而增加，但变异系数较为稳定，变异系数＞15%，说明数据较为离散，但也和统计时未根据母兔的带仔数进行分类有关。

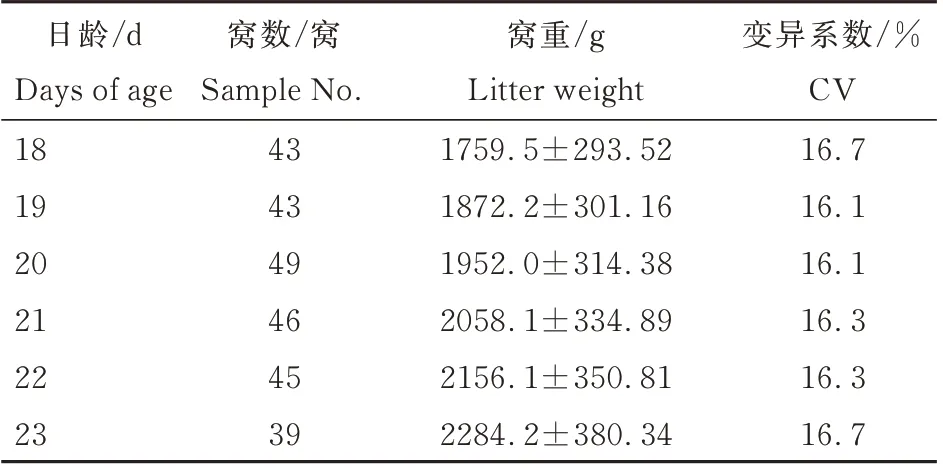
表1 海狸色獭兔18～23 日龄窝重的描述性统计量Table 1 Descriptive statistics of litter weights of Rex rabbit at 18～23-day-old

2.2 拟合方程参数估计

参考1.2.2 中美国养猪协会21 日龄窝重校正公式的形式，分别采用lm 函数拟合二元一次方程和二元二次方程，拟合结果如表2 所示。

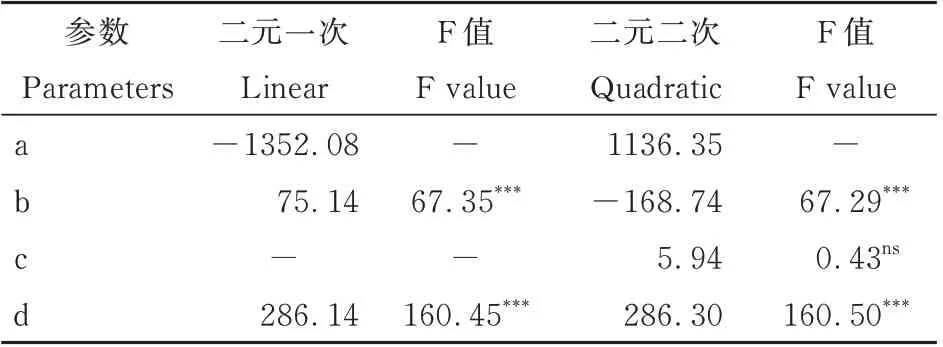
表2 两拟合方程的参数估计Table 2 Parameters estimation of two fitting equations

由表2 可知，采用R 语言中lm 函数分别进行了二元一次和二元二次方程的拟合。二元一次方程各拟合参数通过统计检验均为极显著（P＜0.000 1）；二元二次方程各拟合参数除二次项系数外其它参数统计检验也为极显著（P＜0.000 1）。说明该数据集的线性拟合方程为线性，不需要二次项。

采用anova 函数和AIC 函数进行两拟合模型效果的评估。运行anova 命令后，得到F 值为0.792 6，P值为0.374 2，说明两模型拟合效果差异不显著。AIC 函数的运行结果显示：二元一次方程的AIC 值为3559.08，二元二次方程的AIC 值为3560.28，根据AIC 准则，从一组可供选择的模型中选择最佳模型时以AIC 值最小时为最佳，故二元一次方程优于二元二次方程。

通过拟合参数的检验和模型拟合效果的比较，认为针对本研究的数据集二元一次方程拟合效果较好，因此采用方程：窝重（y）=-1352.08+75.14×日龄（x1）+286.14×带仔数（x2）。

2.3 拟合效果的评估

采用R 语言中plot 函数进行模型拟合效果的常规评估，plot 函数可进行线性模型诊断图的绘制，包括残差分布图、QQ 图、等方差检验图、Cook’s 杠杆值和离群点［14］。运行该命令后得到的模型诊断图如图1 所示。

图1 拟合模型的诊断图Fig.1 Diagnostic plots of fitting equations

由图1A 可知，残差与模型估计值之间呈现轻微的二次关系，说明此模型的残差略微偏离理想的正态分布；Normal QQ 图可检测残差是否为正态分布，若为正态分布，则基本呈线性。由图1B可知，残差基本为正态分布，但存在一些离群点造成QQ 图略微偏离直线。理想的线性模型中，方差应为一定值，若方差随平均值变化较大，则拟合模型的可靠性较差。图1C 中，方差随均值略有波动，但基本变化不大，可认为对模型拟合效果影响不大。Cook 距离图则是分析数据集中一些特别极端的点。图1D 中标出了一些离群点，这些点可能影响了方程的拟合度。

通过运行summary 函数，得到方程的拟合度R2=0.476 4，拟合度偏低，所以对上述检验的离群点和异常点进行剔除。剔除后拟合度R2可达到0.5，但各参数的估计值变化不大。

2.4 21 日龄窝重校正模型的制订

将2.1 中各参数的估计值代入模型中，可推导出如下校正公式：

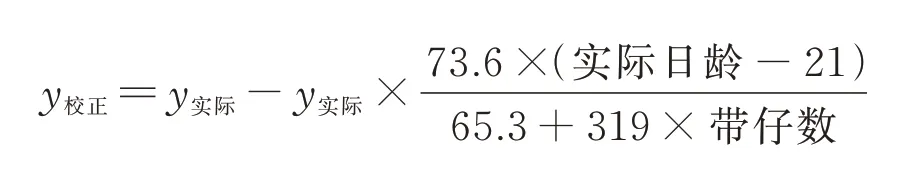
y校正=y实际+y实际×C

将不同测定日龄和带仔数代入上式，得出的校正系数如表3 所示。相同日龄，校正系数（C）随着带仔数的增加而下降。当测定日龄＜21 d 时，校正系数（C）＞1，当测定日龄＞21 d 时，校正系数（C）＜1。

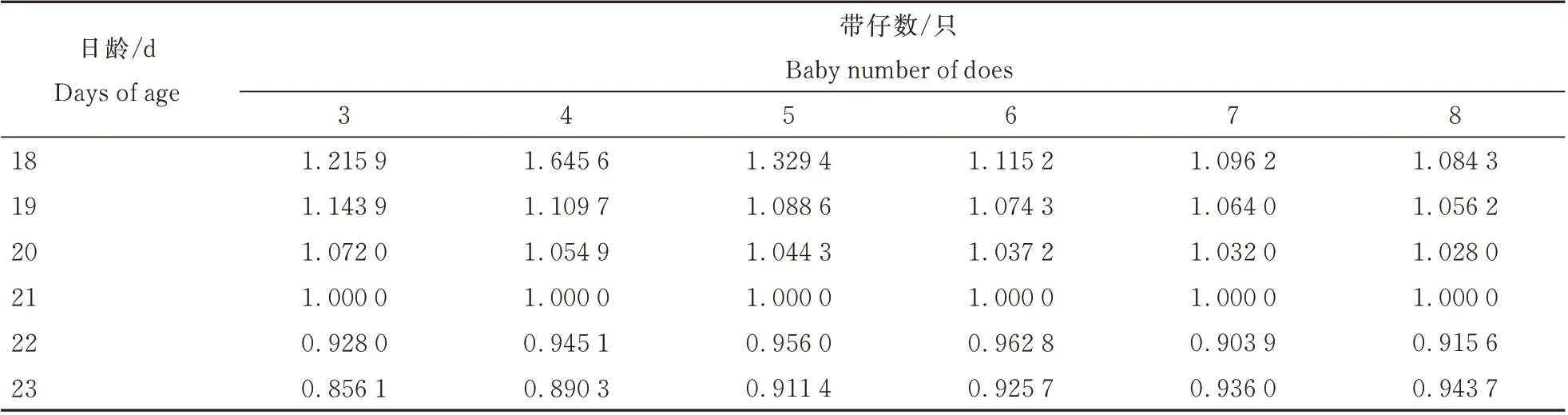
表3 不同日龄和带仔数的校正系数Table 3 Correction coefficients of different ages and litter sizes

2.5 21 日龄窝重拟合度（R2）计算

将不同日龄的校正系数带入公式，计算18～23 日龄窝重校正值并计算拟合度（Rd 2）和所有日龄校正值得总拟合度（R2）。19 日龄拟合度最低，18、22 和23 日龄拟合度都较高，18～23 日龄总拟合度为0.68，说明上述校正公式具有较高的拟合水平（表4）。

表4 不同日龄窝重校正值的拟合度Table 4 Fitting degrees of litter weight at different ages

3 讨论

本研究采用的50 窝仔兔窝重数据均为本单位选育的海狸色獭兔，具有较为一致的遗传背景、体况、胎次和日龄。分析前对数据集中极端值（产仔数≥9 和≤2）进行了剔除，保证了数据的离散程度较低且基本符合正态分布。

从数据的离散程度来看，变异系数（CV＞16%）较高，一般规定正常数据的离散程度不超过15%［15］，变异系数的计算未根据母兔带仔数进行分类，这可能是导致数据离散程度计算值偏高的原因。但从拟合效果图来看（图1A、1B），数据并未偏离正态分布，考虑到数据量较小，所以未对个别离群点进行剔除，这可能也是导致变异系数偏高的原因。

本研究采用50 窝仔兔窝重数据对海狸色獭兔泌乳力进行校正，通过将校正数据与实测数据进行比较，得到该校正公式的总拟合度为0.68，拟合度较高。陈颖［11］参考美国养猪协会校正公式，利用华南种猪遗传评估网1998-2011 年间的数据对长白猪断奶窝重进行了校正，得到公式的拟合度为0.997。该研究采用的数据量较多，且对数据进行了筛选和剔除，获得的拟合公式拟合度很高。彭兴等［16］对10 364 头种猪体尺进行测定，并且按照品种、性别和日龄进行分组，以体重为115 kg 对体重进行校正，得到拟合度很高（R2＞0.99）的分段拟合方程。说明数据量对于校正公式的拟合效果具有较大影响，后续应收集更多的连续日龄数据对校正公式进行改进。Wood 等［17］对64 窝杂交猪后代21 窝重（断奶重）进行了校正，获得的拟合度R2=0.997。该研究数据量与本研究相近，但连续收集了10～32 日龄的窝重数据，具有较长的时间跨度，可以更好的反应窝重变化的趋势，这也是本校正公式进行完善的一个方向。

通过对不同日龄校正系数下拟合度进行计算发现19 和20 日龄数据拟合度较差，而18、22、23 日龄数据拟合度很高，从而导致总的拟合度下降。由于獭兔的生长符合动物生长的Logistic 曲线［18-20］，在早期生长发育接近线性，后期逐渐平缓，可能仔兔窝重增长也具有非线性性，在19 日龄附近正好处于窝重的拐点处，拟合度较低，但具体原因需要扩大数据量后进一步进行分析。本研究也采用了二次方程对数据进行了拟合，拟合度与一次方程接近，考虑到生产中应用的简便性，选择了一次方程作为最终校正公式制订的依据，若希望得到更好的拟合度，可以采用二次、指数、对数等多种方程进行拟合。

本研究采用二元一次方程对海狸色獭兔18～23 日龄窝重数据进行了拟合，得到合理的二元一次拟合方程，并进一步推导出泌乳力的校正公式。由于在实际生产中有时不具备准确称取21 日龄窝重（泌乳力）的条件，而泌乳力又是母兔繁殖性能的一个重要指标，因此，制订校正公式具有一定的实用价值，可以在生产中进行推广使用。

本研究参考猪上的断奶窝重校正公式制订方法推导出适用于海狸色獭兔21 日龄窝重的校正公式。需要注意的是，此公式不适用于产仔数过多（多于10 只）或过少（少于2 只）的母兔；另外，由于仔兔从出生到断奶的过程窝重变化为非线性，此公式适用的日龄范围为18～25 日龄对母兔的泌乳力进行校正，在此范围之外校正的准确性偏差较大，不建议使用。此公式适用于獭兔，对于肉兔或毛兔，由于其生长期不同，所以不建议使用。

4 结论

本研究采用海狸色獭兔仔兔18～23 日龄的连续窝重数据，制订了獭兔21 日龄窝重（泌乳力）的校正公式，该公式可用于獭兔19～25 日龄实地测量的窝产仔数校正且带仔数为2～9 只的獭兔，准确度可达到0.7，可在实际生产中推广使用。