基于相对转角与位移的空心板桥铰缝损伤识别

赵强， 黄旭升， 周宇

(1.安徽建筑大学环境与能源工程学院， 合肥 230601; 2.安徽建筑大学安徽省智慧城市工程技术研究中心， 合肥 230601; 3.安徽建筑大学土木工程学院， 合肥 230601; 4.安徽省装配式建筑研究院， 合肥 230601)

空心板桥铰缝在实际使用中做为横向传力部件，易发生损伤[1]。既有铰缝受力分析认为铰缝中只传递垂直剪力作用[2-3]，但实际铰缝空间应力状态较为复杂，既有铰缝分析精度仍有完善空间。实际铰缝不仅受垂直剪切作用，且不可忽略的是，也将受到横向挤压和纵向剪切的影响[4-5]，因此，铰缝变形可以更加精确地概括为竖向剪切变形和横向弯曲变形[6]，其中横向弯曲变形由空心板相对转动引起的不均匀挤压造成。当铰缝出现严重损伤，空心板主梁将处于“单板受力”状态，极大地削弱了空心板梁桥横向传力的连续性与完整性[7-8]。铰缝区域损伤的系统性原因正逐渐成为中外学者研究的热点。

近年来，随着既有桥梁结构性能的退化，桥梁结构损伤识别研究发展迅速，且意义重大。学者们在桥梁损伤识别的应用方面开展了大量研究，杨书仁等[9]采用应变影响线理论，建立了基于应变比的桥梁损伤识别与评估方法；李岩等[10]针对装配式空心板桥常见病害，基于交通荷载下结构动力响应变化特征的量化分析，提出铰缝损伤的评价指标；周宇等[11]提出转角影响线差值曲率，实现了弹性约束支承梁的局部损伤的精确定位和定量。此外，阳洋等[12]采用单元刚度损伤识别的新型间接量测法，实现大面积大区域桥梁集群快速测试；周宇等[13]基于Dempster-Shafer证据理论融合影响线与柔度指标对悬索桥不同位置与程度损伤进行识别敏感性研究。结构发生损坏时，其受力性能下降，结构模型参数随之改变，良好的损伤识别方法可以根据参数指标改变定位、定量损伤[14-17]。然而，由于空心板桥空间受力状态兼具梁桥与单向板的特点，常用损伤识别方法难以定位和量化铰缝损伤。

与既有铰接法相比，有必要提出铰缝损伤定位更加准确、定量损伤程度更为精确的指标方法，以达成更加精细地分析铰缝损伤程度的目的。针对实际工程问题，现建立弹簧铰缝的力学模型，推导了铰缝损伤程度的计算公式，提出一种基于相对位移法的无量纲损伤评估指标，并将铰缝的状态分为4种状态：完好状态、微损状态、损伤状态和失效状态，结合数值分析验证计算理论的有效性，采用MIDAS/Civil建立有限元模型，通过仿真分析比较，以验证铰缝损伤程度计算公式的实用性。

1 铰缝与空心板桥模型

1.1 铰缝简化计算模型

空心板桥典型加载受力状态如图1所示。若集中荷载P施加在跨中，铰缝铰接接头处于较为复杂且集中的应力状态，其截面完整性和变形刚度较现浇空心板主梁更为薄弱。

既有铰接板理论认为，小尺寸、钢筋少的铰缝接头常被设计为“小铰接接头”。吴庆雄等[18]做了加大、加深、加钢筋等构造改进工作，使之成为“中铰接头”或“大铰接头”。然而，作为空心板桥的一个重要力传递构件，铰缝仍为薄弱环节，总是处于较为复杂的拉压、剪切和弯曲的力学状态，据此建立“大铰接头”，如图2所示。

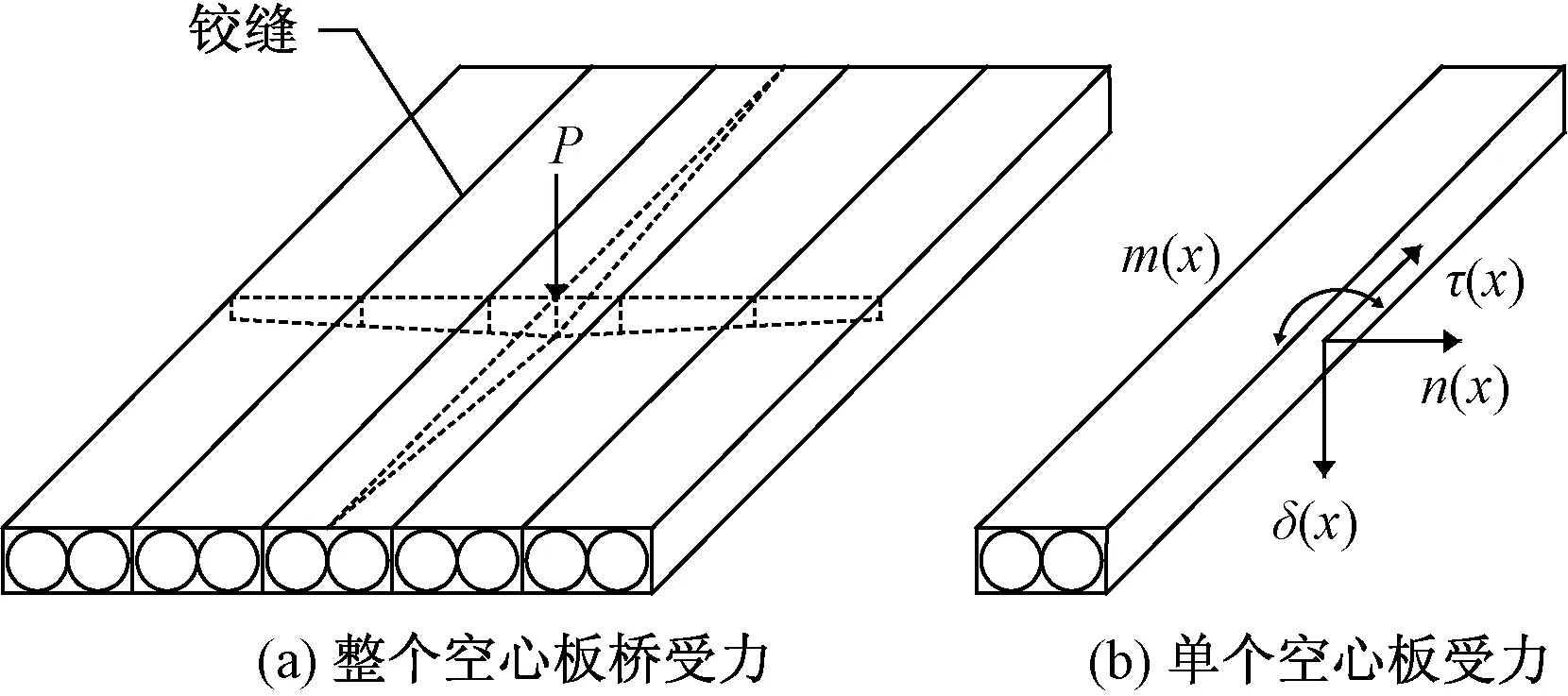
P为集中荷载；τ(x)为切应力；m(x)为弯曲应力； n(x)为水平方向侧向力；δ(x)为竖直方向垂直应力图1 空心板桥受力示意图Fig.1 Schematic diagram of loading of hollow slab bridge

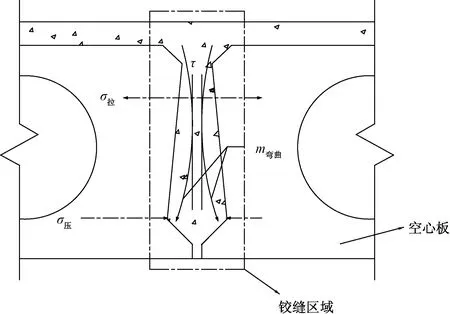
σ拉为横向拉应力；σ压为横向压应力； τ为铰缝内部切应力；m为弯曲应力图2 铰缝应力状态Fig.2 Stress state of hinge joint

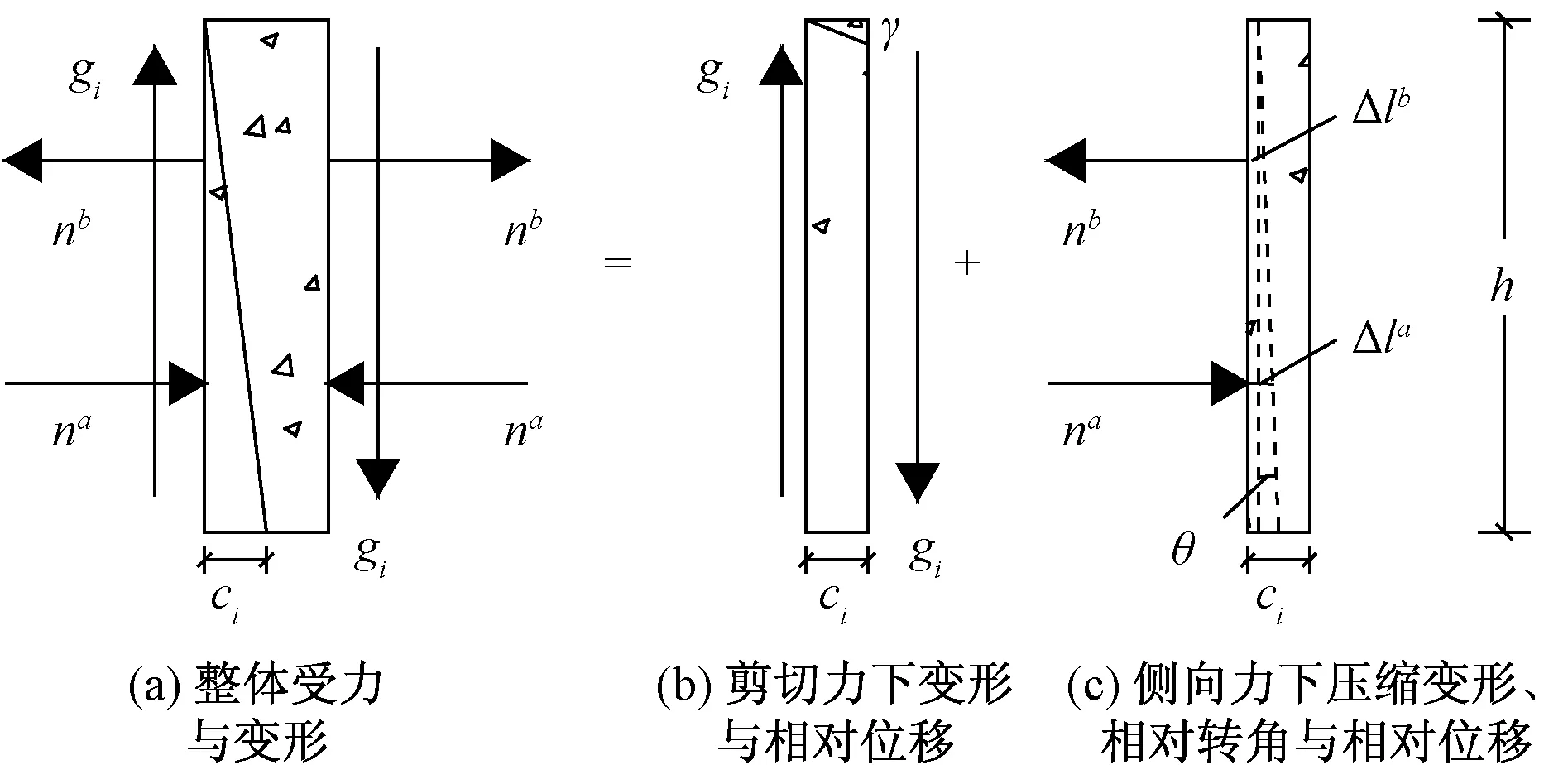
图3 铰缝变形Fig.3 Hinge joint deformationt

为更好地模拟铰缝实际应力状态，以侧向集中力与其矩臂的乘积代替铰缝处弯矩，使铰接接头界面处内力简化为剪切力gi。两组侧向力na和nb通常不等，如图3所示，其中h为铰缝的高度。对图2的整个铰缝进行受力分析，将铰缝拆分为两部分，以铰缝宽度的一半为研究对象，剪力使混凝土产生变形γ，导致空心板发生相对位移ci。此外，侧向力na为压力，nb为拉力，二者会使铰缝引起侧向拉伸或压缩变形l，由于两者不等，会使空心板梁截面发生扭转，从而形成空心板梁变形的相对转角θ。

1.2 铰缝力学模型

根据既有铰接板理论[2]，考虑铰缝横向应力、损伤和变形，提出以下基本假设:①空心板只有纵向挠曲变形，横向为刚性；②板荷载、位移、铰缝剪力、铰缝混凝土侧向力等沿跨呈现半波正弦分布；③铰缝只传递竖直方向剪力和横向侧力，可能不涉及纵向剪力；④不考虑材料泊松比的影响；⑤铰缝位置各空心板间垂直方向的相对位移与剪力大小成正比，与铰缝剪切刚度大小成反比。

基于上述5种假设，绘制出铰缝力学状态分析模型如图4所示。

图4中，在na和nb位置替换为两个弹簧，在铰缝中心替换为一理想铰接杆。通过弹簧和铰接杆与两侧空心板连接，更好地实现了力学模型状态的描述。考虑弹簧只传递轴向力，空心板相对转角可通过弹簧形变计算；理想铰接杆只能传递剪力，因此两个空心板的相对垂直位移可通过铰接杆剪切变形获得。

根据胡克定律，力F作用下每个弹簧的变形为

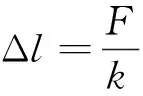
(1)

根据图5，由材料力学剪力与变形微分公式：

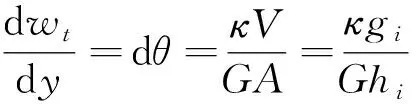
(2)

得出单位长度dy内剪力gi引起剪切变形wt的计算公式：

(3)

式中：G为铰缝材料剪切模量；V为垂直方向的截面剪应力；A为截面面积；V/A为截面平均剪应力；κ为矩形截面剪切系数，κ=3/2。假设截面面积为1,则V为单位剪切力，微元应力状态和变形情况如图5所示。

1.3 空心板桥计算模型

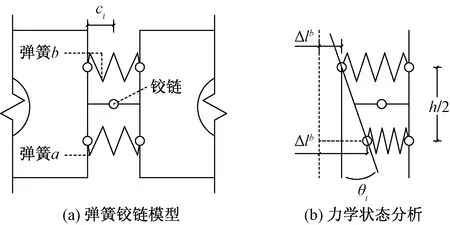
图4 铰缝力学状态分析模型示意图Fig.4 Schematic diagram of the hinge mechanical state analysis model

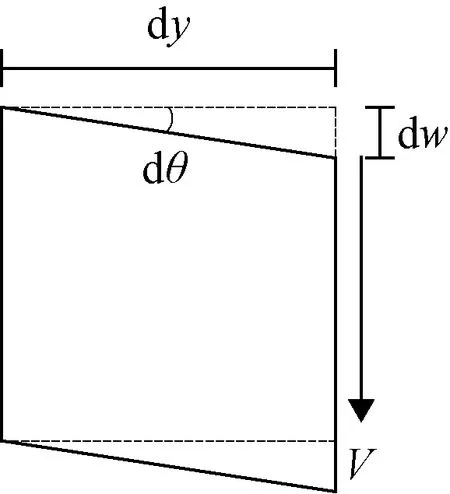
图5 微元应力状态和变形Fig.5 Stress states and deformations of micro-elements

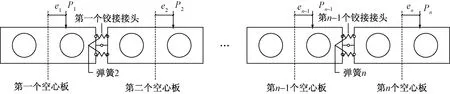
Pi为竖向荷载；ei为荷载偏心距图6 空心板桥力学模型Fig.6 Mechanical model of hollow slab

基于上述假设和铰缝的力学模型，空心板桥即为中间连接弹簧和铰接杆的一系列空心板，如图6所示。空心板从左到右依次编号为1～n，相应的铰缝顺序为1～(n-1)。物理量的正方向定义如下：①空心板竖向荷载和位移向下为正；②竖向偏心荷载和剪力引起的空心板旋转弯矩顺时针为正；③铰缝处各空心板间相对位移左侧向下为正，右侧向上为正；④铰缝混凝土受压时侧向力为正；⑤铰缝相对旋转角左侧顺时针为正，右侧逆时针为正。

对于第i个空心板，将竖向荷载Pi、竖向铰缝剪力gi和侧向力ni等影响叠加，如图7所示(图7中方向均为正)。

2 铰缝损伤计算

2.1 考虑挠度的铰缝损伤计算方法

实际工程不同于既有的铰缝模型，各种不利因素或破坏会导致相对位移产生，考虑到铰缝剪切刚度和材料弹性模量，通过降低弹性模量引入相应损伤，即从Gj到(1-Dj)Gj。根据式(2)，剪切力引起的相对位移近似计算公式如式(4)所示,以式(4)所得位移作为铰缝变形协调条件，铰缝的力法方程公式如式(5)所示。

图7 第i个空心板受力计算Fig.7 The i hollow plate force calculation

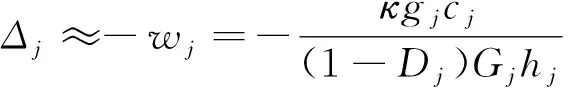
(4)

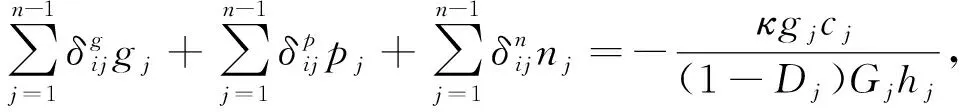
i=1,2,…,n-1

(5)

2.2 考虑相对转角的铰缝损伤计算方法

考虑到铰缝处侧向力，假定铰缝与空心板交界面无损伤，力学模式如图4所示。弹簧具有相对刚度，相对转角计算公式为

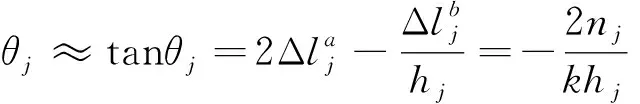
(6)

采用式(6)作为铰缝变形协调条件，考虑相对转角，力法方程为

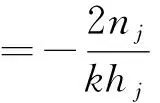
(7)

式中：θ为不同的相对转角，分别由第j个铰缝处单位剪力，第j个空心板上的单位垂直载荷和第j个铰缝处的单位侧向力作用下在第i个铰缝处产生。

2.3 铰缝单位力作用下的相对位移计算

空心板的宽度都为b；θg、θp和θn为空心板在各单位力下产生的角度。根据作用力的叠加原理(图6)和图8～图10，不同因素产生的相对位移

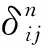
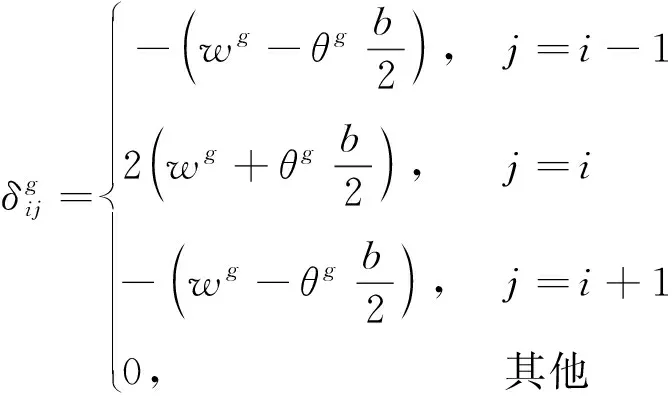
(8)

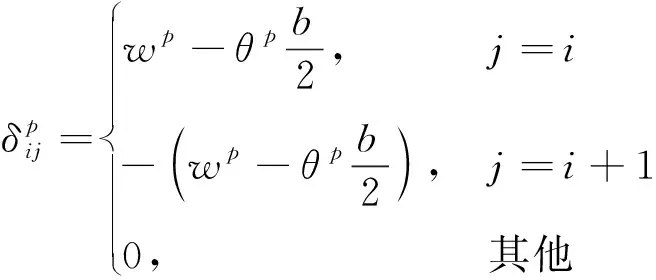
(9)

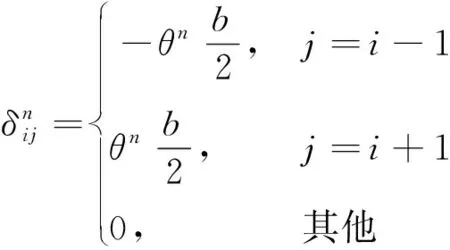
(10)

式(8)与式(9)中的垂直挠度ωg和ωp等值，但由不同性质的单位力产生，区分标注。

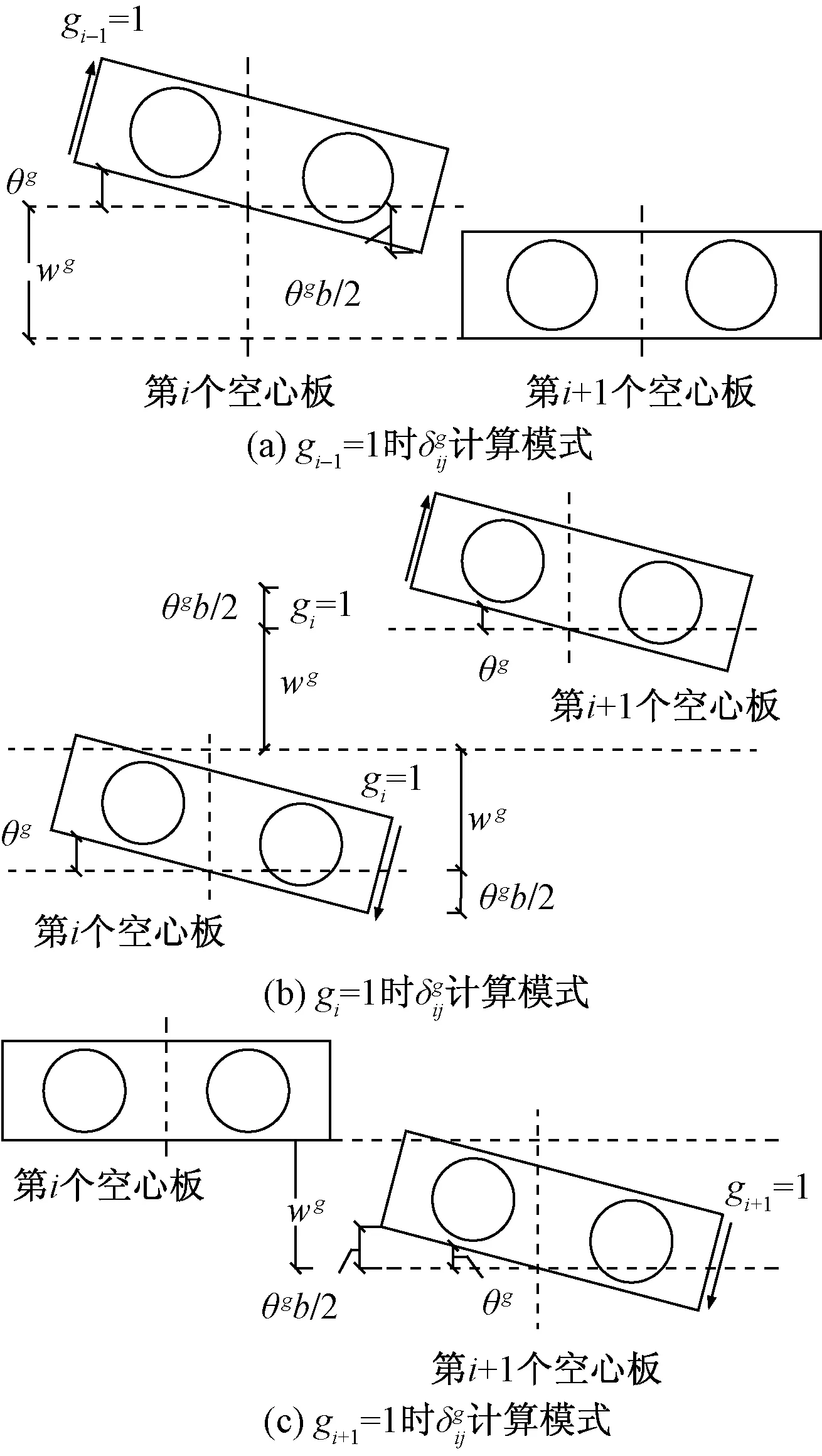
图的计算模式Fig.8 The calculation mode of

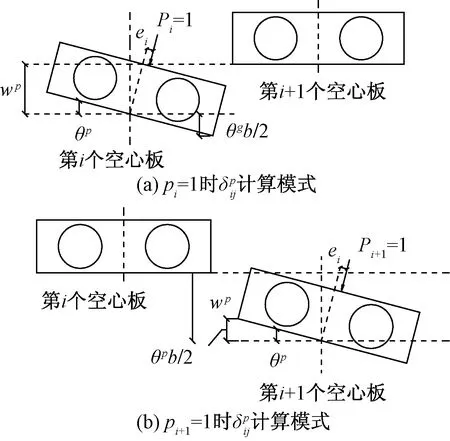
图的计算模式Fig.9 The calculation mode of

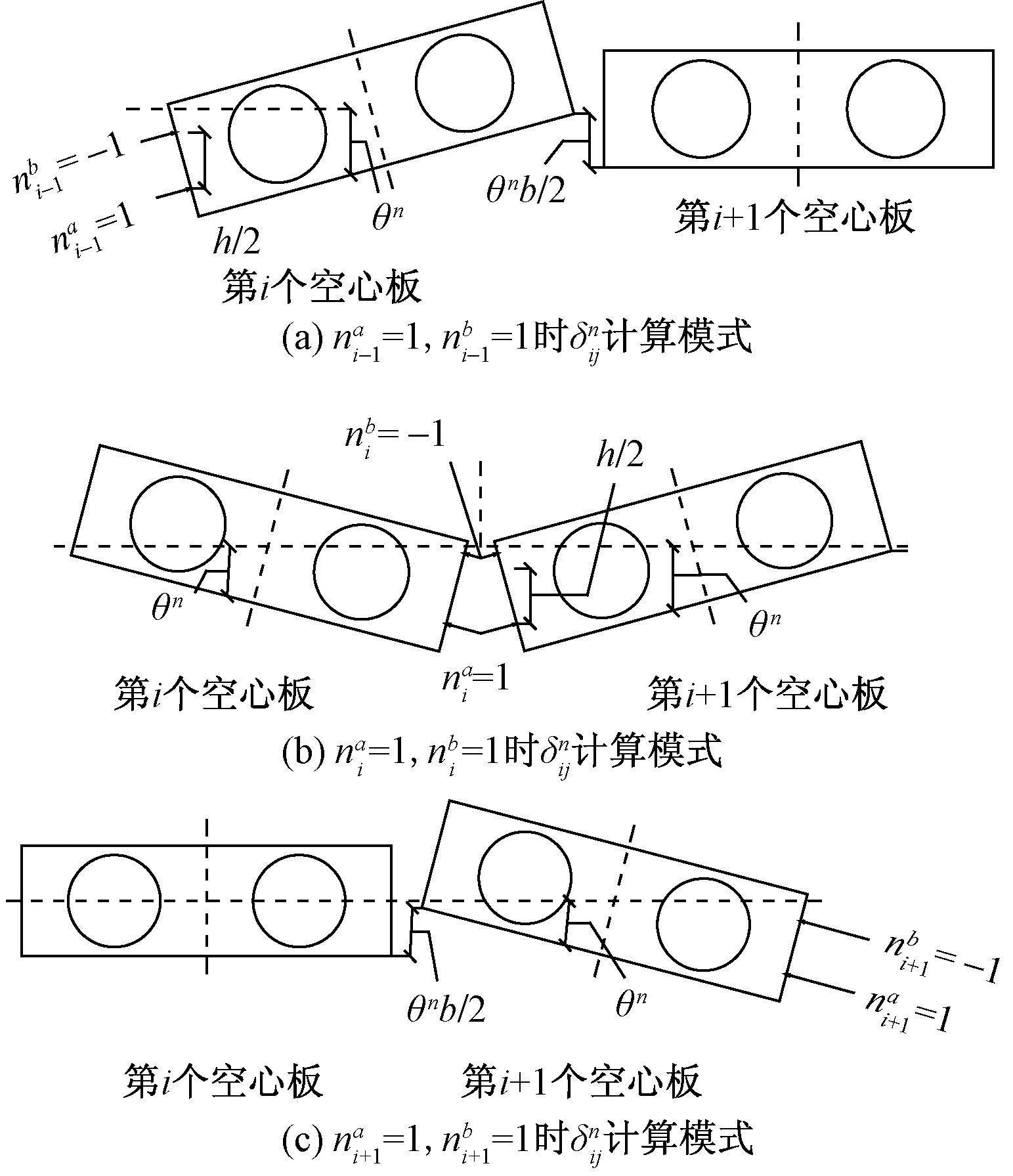
图的计算模式Fig.10 The calculation mode of

对于第j个铰缝，由剪力g、荷载p和侧向力n产生的转角与位移，受第j-1和j+1个铰缝的剪力g和侧向力n影响，且与相邻的第j和第j+1个空心板上的荷载p有关。

2.4 铰缝单位力作用下的相对转角计算

根据图8～图10，由不同因素产生的相对转角

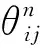
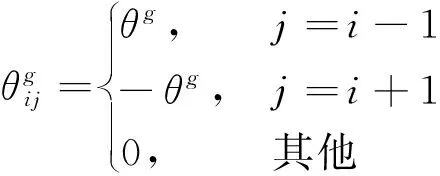
(11)

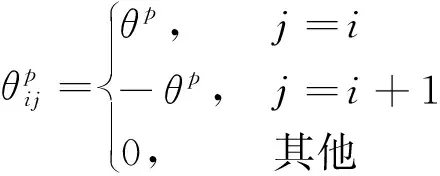
(12)

(13)

2.5 铰缝剪力计算

在空心板桥上施加一组纵向正弦分布荷载，同截面上板中心竖向位移f与其荷载Q成正比。根据参考文献[8]中描述的方法计算铰缝剪切力，假设每个空心板大小相同，荷载和剪力公式为

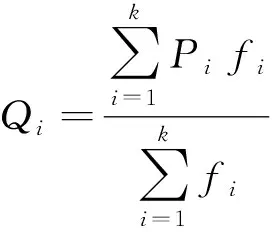
(14)

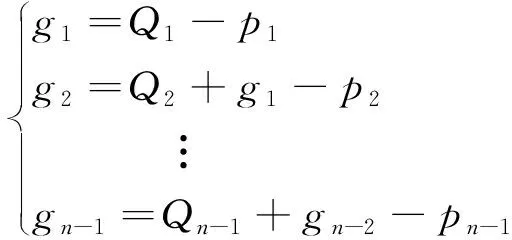
(15)

2.6 铰缝损伤程度Dj计算

将每个空心板(i=1，2，…，n-1)的荷载pi，式(11)～式(13)中相对转角

损伤度Di(i=1，2，…，n-1)代表铰缝剪切刚度的退化度，将R=(1-Di)(i=1，2，…，n-1)定义为剩余度。可以推导出系数i与剩余度。可以推导出系数i与剩余度R成反比，，利用相似三角形法计算相对位移fi，根据公式计算得到正弦分布荷载Pi，结合式(14)和式(15)可计算得到剪力gi，将和α代入式(16)得到侧向力ni，代入式(17)，求解未知量i，然后根据式(18)计算铰缝的损伤程度Di。

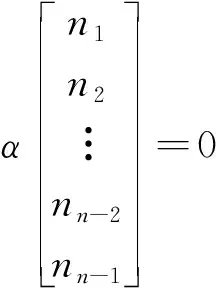
(16)

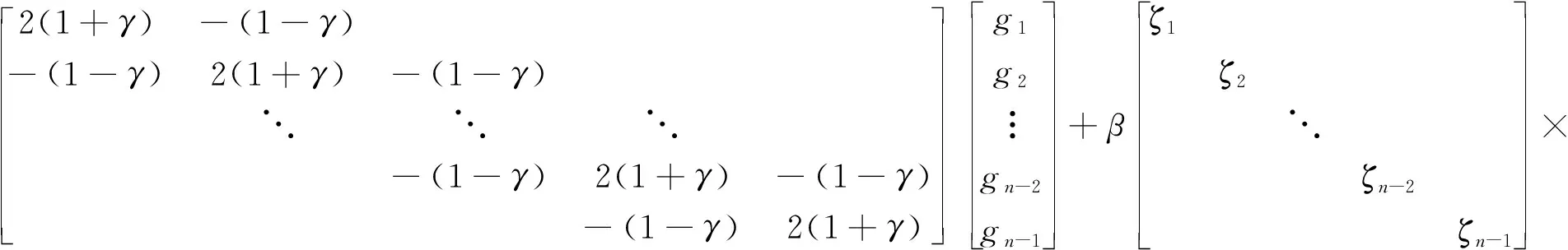
(17)

式中：

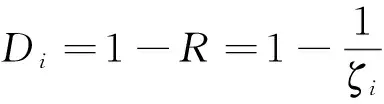
(18)

3 数值模拟

3.1 实桥概况和加载实况

以单跨简支空心板梁桥为例进行模拟，跨度10 m，由10块空心板铰接，如图11(a)所示。各空心板的宽度为1 000 mm，高度为950 mm，各铰缝计算宽度为120 mm。此外，该结构中所用的混凝土的强度等级为C30。利用有限元软件MIDAS/Civil建立有限元模型，如图11(b)所示。模型共有节点 1 222 个，梁单元1 015个，桥面铺装采用410个板单元。

采用虚拟横梁模拟铰缝，采用降低单元刚度模拟损伤发生[19]，降低虚拟横梁刚度引入损伤。铰缝作为单元间横向连接的核心，包括两个部分，一个只受到称为铰链连接弹簧元件的横向力，在1/4和3/4的高度连接两个空心板，另一个只受到称为铰链连接杆元件的垂直力，其设置在空心板高度的 1/2 处，如图11(c)所示。

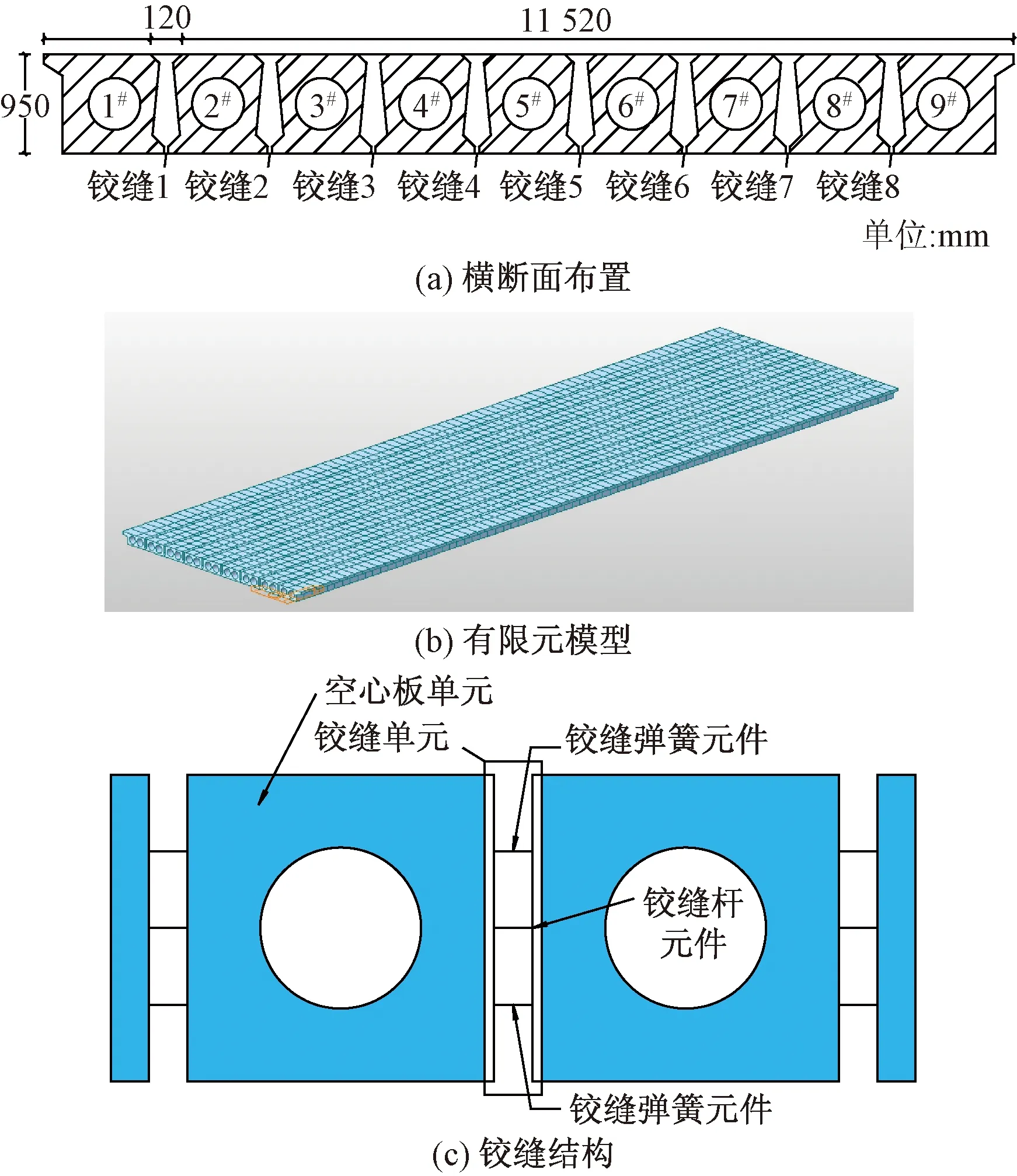
图11 空心板桥横断面布置与数值模拟的有限元模型Fig.11 The finite element model of transverse layout and numerical simulation of hollow slab bridgel

此外，铰缝的刚度也与铰缝的材料特性、宽度、高度和间距有关。根据铰缝的应力和变形，铰缝刚度为

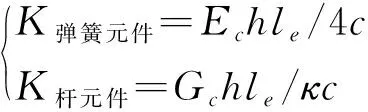
(19)

式(19)中：Ec、Gc为混凝土的弹性模量与剪切模量；le为铰缝的间距；h为铰缝的高度；c为铰缝宽度的一半；κ为矩形截面的截面剪切系数，取κ=3/2。

以空心板桥跨中为典型研究截面，用横向虚拟梁为了简化计算。采用中浓度负荷(P=100 kN)进行了负荷计算和分析，负载情况分为未损伤情况和损伤情况。

根据负载和损坏位置，将未损伤的情况划分如下：①未损伤的工况1(荷载作用于第2个空心板中心)；②未损伤的工况2(荷载作用于第3个空心板中心)；③未损伤的工况3(荷载作用于第6个空心板中心)。

根据载荷和损伤位置，损伤情况定义如下，损伤模拟以横向虚拟横梁刚度下降实现。①损伤工况1(完全的损伤发生在第2个铰缝并且载荷作用于第2个空心板中心)；②损伤工况2(完全的损伤发生在第2、3个铰缝并且载荷作用于第3个空心板中心)；③损伤工况3(完全的损伤发生在第2个铰缝并且载荷作用于第6个空心板中心)；④损伤工况4(完全的损伤发生在第6、7个铰缝并且载荷作用于第7个空心板中心)。

3.2 计算结果

根据文献[4，11]的方法，将式(16)和式(17)中的跨中集中力P替换为半波正弦荷载，代入式(16)和式(17)进行计算。跨中荷载的峰值计算为pi(p1，p2，…，pn-1)，pi=2Pi/L，其中L为桥梁的跨度。具体计算结果如下。

(1)剪切力计算结果与数值模拟结果相差不大。最大误差发生在损伤工况1的第5个铰缝，且差值为0.53 kN/m，结果如图12(a)所示。

(2)铰缝侧向力计算值与数值模拟值吻合较好，最大误差在损伤工况1的第5个铰缝，差值为4.67 kN/m，结果如图12(b)所示。

(3)在跨中段，空心板铰缝相对位移的计算结果表明，在最大误差在损伤工况1的第5个铰缝，差值为0.09×10-2mm，结果如图12(c)所示。

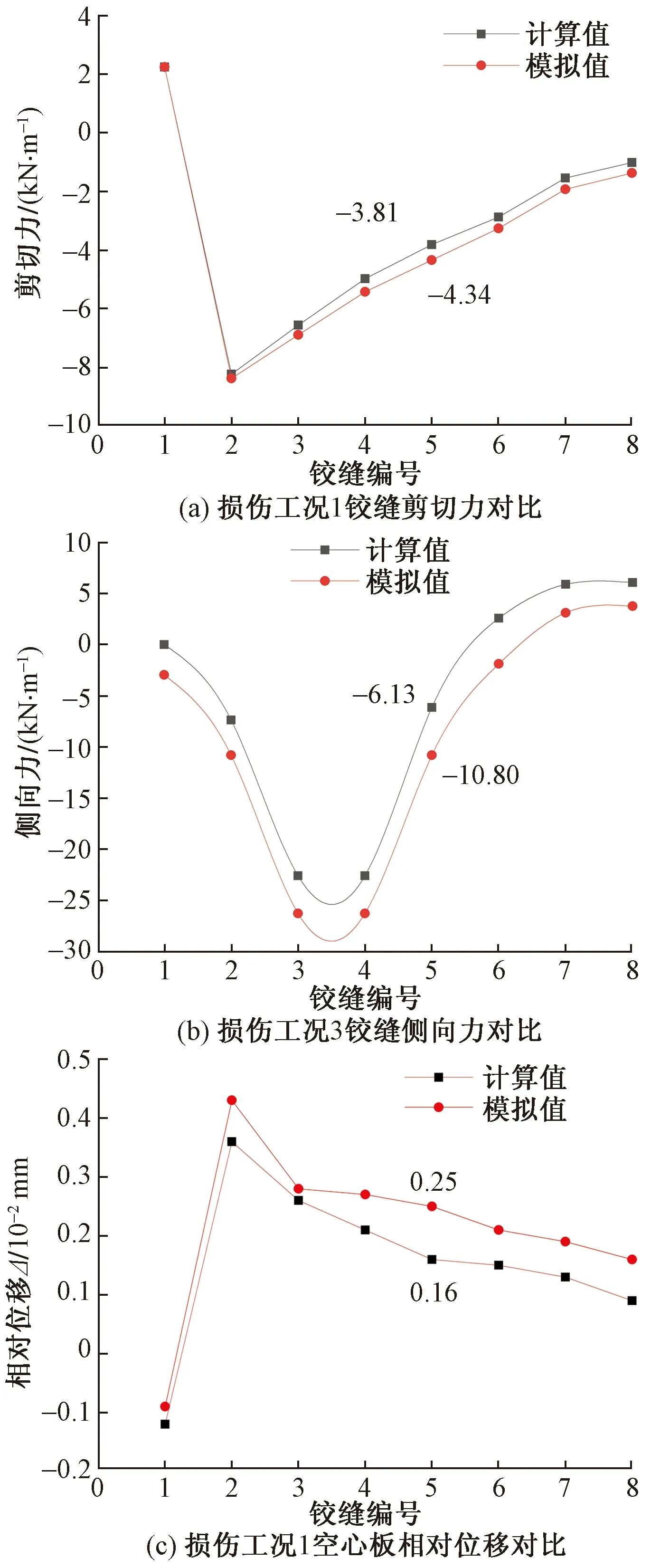
图12 各种工况铰缝剪切力、侧向力和空心板相对位移对比Fig.12 Comparison of shear force, lateral force and relative displacement of hollow plate under various working conditions

由计算结果及图12可知：①考虑铰缝横向力影响的情况下，计算所得的空心板相对位移通常小于模拟值；②可以确定铰缝的损伤位置，也能够描述损伤程度。

损伤工况1和损伤工况4的损伤程度计算结果与预设值对比如图13所示。

图14总结了损伤工况1、损伤工况2和损伤工况3的损伤程度计算结果。可以发现，加载区域越接近损伤位置，损伤定位的精确性越显著，损伤程度识别结果的准确性越高。

式(16)～式(18)中，由于计算结果会受到荷载位置的影响，公式与数值模拟结果吻合较好，可达到损伤位置识别的目的，且可以定量评估铰缝损伤程度的相对大小。通过建立铰缝力学模型，推导出损伤程度计算公式，代入数值计算验证公式实用性，实现损伤定位、定量，验证了文章的理论相较既有铰缝理论，具有更高的精确性。

4 实桥案例分析

4.1 静载试验概述

试验桥为三跨简支预制空心板桥，总长42.64 m，标准跨长13 m，横向宽度12 m，桥梁上部结构为9块组装好的空心板，由8个铰缝连接，形成一个整体。桥面路面层为现浇混凝土沥青，两侧设混凝土防撞护栏。本项目工程概况如图15所示。

桥梁各空心板宽1.24 m，板高0.55 m，板与铰缝以及截面布置如图16所示。

对该桥进行静载试验，车横向轴距1.9 m，纵向轴距4.7 m，前桥重62.13 kN，后桥重223.93 kN，如图17所示。

进行静载荷试验时，对桥梁最不利载荷位置进行车辆加载和数据采集，获得各空心板竖向挠度。在桥梁中跨段设置垂直位移测点，采用YD-10型位移传感器进行测量，如图18所示。

此外，测试设置了两种类型的车辆装载案例，如图19所示。车辆布置于跨中段，根据位置的不同，装载分为以下两种工况：①加载工况1(装载车较重轴设置在中跨1/4段)；②加载工况2(装载车较重轴设置在中跨1/2段)。

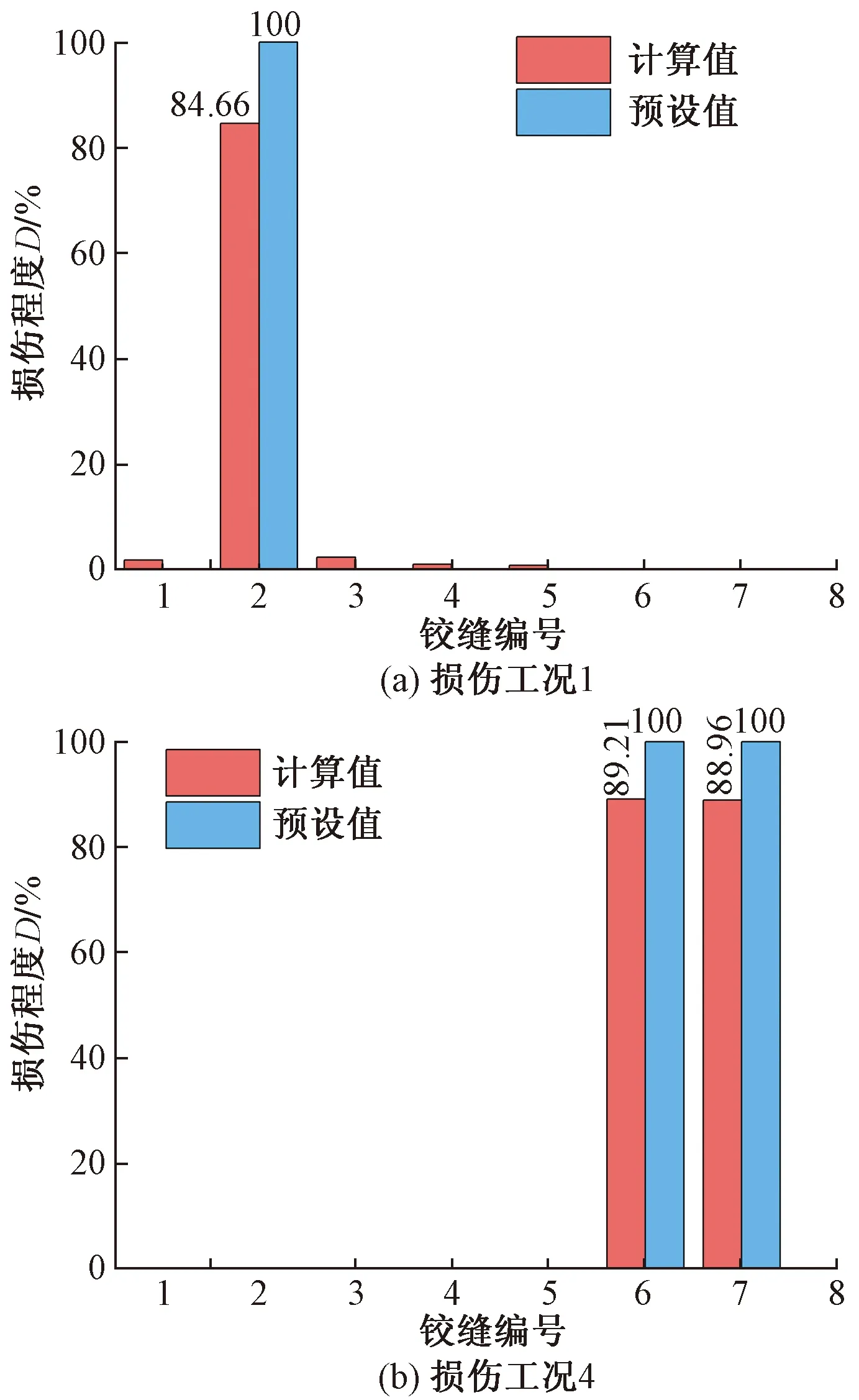
图13 不同工况下铰缝的损伤程度对比Fig.13 Comparison of the damage degree of the hinge joints under different working conditions

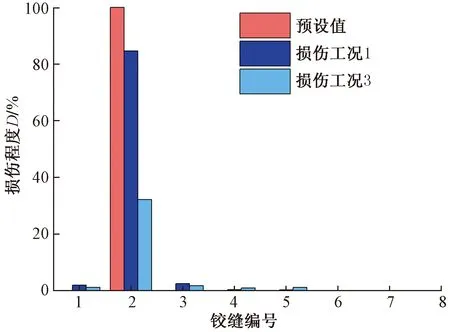
图14 荷载位置对损伤程度的影响Fig.14 Effect of the load position on the degree of damage

图15 本项目工程概况Fig.15 Project overview of the project

图16 桥梁构件编号及横断面布置Fig.16 Bridge component number and cross-section layout

4.2 试验结果分析

数值模拟得到空心板挠度的理论值，根据位移传感器YD-10采集实测值。整理出理论(T)和实测(M)值；根据式(16)～式(18)，代入挠度的实测值，计算接头的损伤程度D。限于篇幅计算过程未作详细赘述，跨中空心板中心挠度值和铰缝损伤程度D计算结果如表1和表2所示。

根据工况1、2中铰缝损伤程度D的计算结果，取平均值O评价铰缝，结果如图20所示。

损伤程度在第3、第6和第7个铰缝处最大，分别达到了99%、94.5%和83%，处失效状态；第1和第5个铰缝损伤程度较大，分别达到69%和60%，处损伤状态。建议对第3、第6和第7个铰缝进行重建，对第1和第5个铰缝进行修复。

5 结论

(1)混凝土空心板桥铰缝主要受侧向力和剪力作用的影响，证明本文中提出的弹簧铰缝力学模型是可行的。铰缝的受力状态较为复杂，在考虑剪切传递的同时，铰缝的侧向力也不容忽视。基于铰缝侧向力、剪切力产生的损伤和变形，建立空心板桥铰缝计算模型，推出铰缝损伤程度的计算公式，将相对挠度、剪力和相对转角代入公式，可定量计算出铰缝损伤程度，且可更精确发现铰缝损伤部位。

(2)通过有限元法的仿真分析和实际桥梁静负载试验，所提出的计算公式与仿真和试验结果吻合较好，并能够识别铰缝的损伤位置和程度，加载区域越接近损伤位置，损伤定位的精确性越显著，损伤程度识别结果的准确性越高。

(3)本文中将铰缝的状态分为4种状态：完好状态、微损状态、损伤状态和失效状态，通过MIDAS/Civil建立有限元模型，通过仿真分析比较结合数值分析验证了计算理论的有效性，铰缝损伤程度计算公式的实用性，可得出损伤程度D的具体值，并对损伤程度达到50%及以上的铰缝进行列举分析，并给出修改意见，具有较高的实用价值。

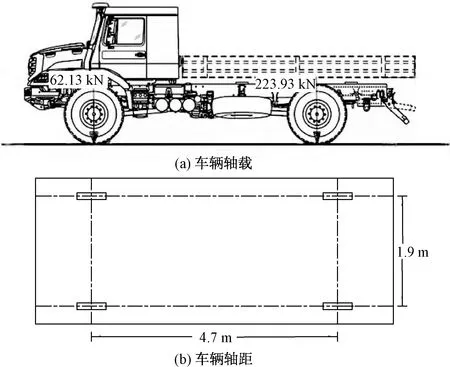
图17 装载车辆示意图Fig.17 Schematic diagram of loading vehicles

图18 测量点的布置情况图Fig.18 Layout diagram of measuring points

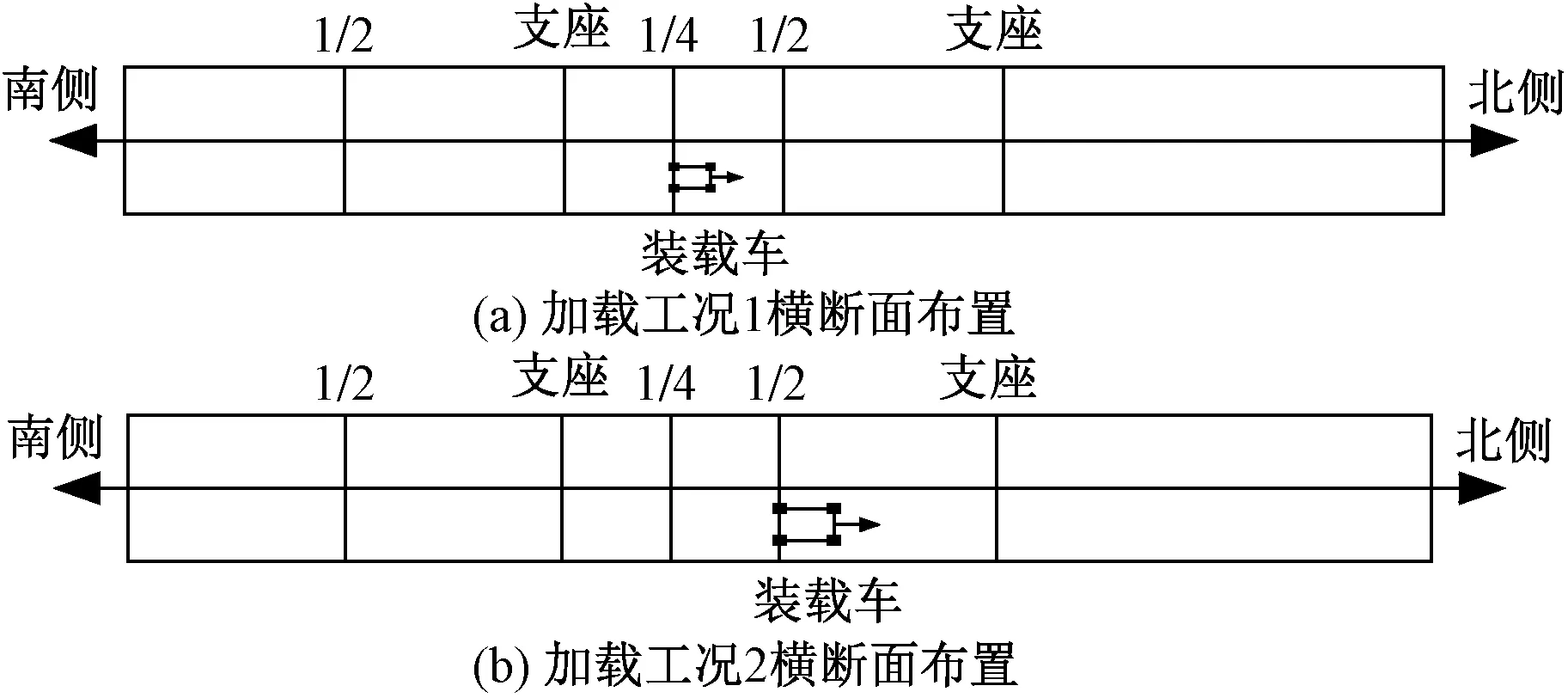
图19 装载工况平面图Fig.19 Loading plan

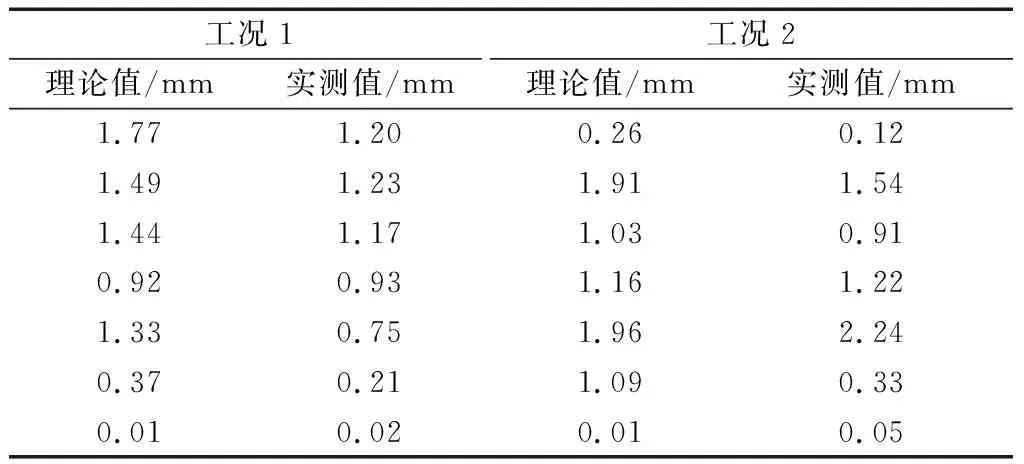
表1 跨中板中心挠度值

表2 铰缝损伤程度D计算结果Table 2 Calculation results of hinge joints damage degree D

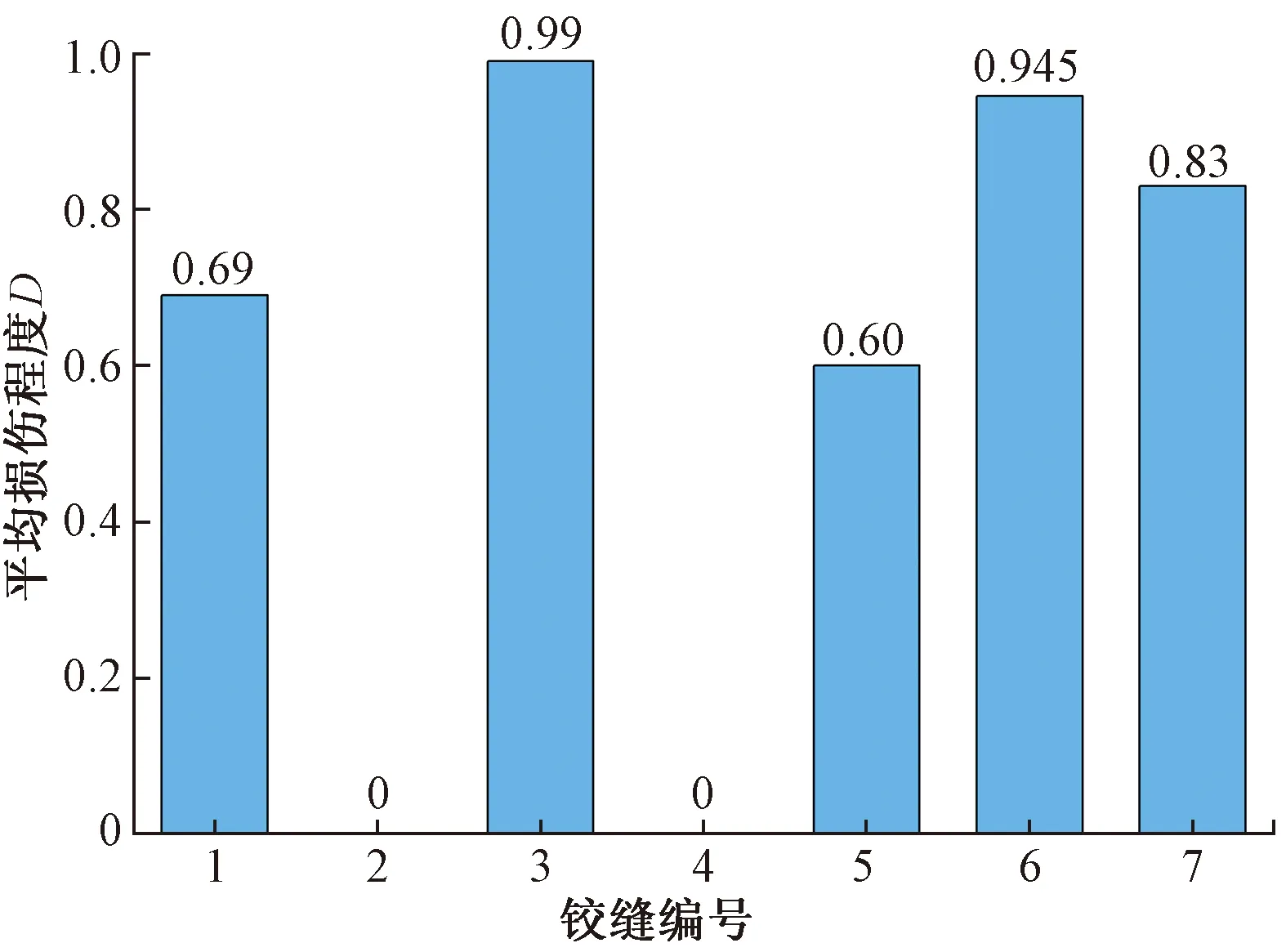
图20 损伤程度的计算结果Fig.20 Calculation results of the damage degree