基于铰缝破坏程度对桥梁荷载横向分布影响的研究

陈俞宏，曹新建，2

（1.浙江省建设工程质量检验站有限公司，浙江 杭州 310012；2.浙江省建筑科学设计研究院有限公司，浙江 杭州 310012）

1 铰接板法理论

混凝土企口缝连接的装配式空心板桥（图1），2＃板承受荷载P作用，除了2＃板本身引起的纵向挠曲外，其他板块也会受力发生挠曲变形。这主要是因为各板之间通过结合缝所承受的内力在一起传递荷载作用。由于企口缝的高度不大，刚性弱，通常视作铰接，所以假定竖向荷载作用下，铰接缝只传递竖向剪力g（x）。

图1 空心板受力整体挠曲示意

对于n条板梁组成的桥梁，必然有n-1条铰缝，在板梁间沿铰缝切开，则每个铰缝内作用着一对大小相等、方向相反的内力。因此，对于n条板梁，就有n-1个欲求的未知力gi，则根据力的平衡原理，可得分配到各板块的竖向荷载Pi1。如图2所示，以5块板为例。对于具有n-1个未知铰接力的超静定问题，总有n-1个铰缝，将每个铰接缝切开形成基本体系，假设铰缝完好，利用相邻板块在铰缝处的竖向相对位移为零的变形协调条件列出矩阵方程式（1）。

图2 空心板受力横截面计算

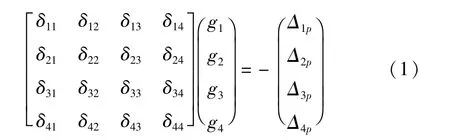
根据铰缝及梁板的扭转及挠曲的变形协调条件，δik和Δip均可利用材料力学中的公式求得。故可以得出方程的解式（2）如下所示：

同理，P＝1作用其他板块时也可求出铰缝内力，从而可得到各板块的荷载横向分布系数影响线［1-2］。

2 实例分析

2.1 工程概况

某桥位于临海市，为单跨简支梁桥，跨径13 m。机动车道为四车道，由18块空心板铰接形成，梁板高0.6 m，宽1.0 m，主梁、铰缝采用C50混凝土。桥梁下部结构采用重力式桥台。在对该桥进行结构定期检测时，发现2条铰缝存在严重的破坏现象，部分位置铰缝连接已经完全失效，分别位于2＃板到3＃板间，5＃板到6＃板间，见图3。

图3 板间铰缝失效

2.2 铰缝破坏模拟

空心板之间通过现浇混凝土企口铰缝连接，当铰缝发生开裂破坏时，桥面铺装在铰缝处会形成纵向开裂，这样铰缝连接刚度会折减；所以，为了模拟铰缝破坏程度，利用企口缝混凝土弹性模量折减的方法实现［3］，见图4。本桥2＃～3＃和5＃～6＃间的铰接缝刚度按8个等级进行折减划分。

图4 铰缝破坏示意

3 模型数据分析

3.1 计算模型

利用Midas/Civil建立全桥模型，利用铰接板法理论来模拟实际结构，两端简支，共设置72个支座。根据铰接板法理论，梁板间的连接可视作铰接，所以在Midas/Civil模型中设置虚拟横梁来模拟横向连接，其板宽取1 m，板厚取空心板顶板厚度［4］。在主梁交接处需要对虚拟横梁增设节点且释放该节点的横向弯矩来模拟板间铰接。弹性模量E取3.45×104MPa，见图5。

图5 整体计算模型

3.2 加载荷载

该桥梁设计荷载等级为公路I级，采用车道布载为最不利加载方式，4车道加载。限于篇幅本文只讨论在偏载工况下1＃～8＃空心板的桥梁荷载横向分布情况［5］。

3.3 计算结果分析

3.3.1 铰缝刚度折减下各空心板跨中位置截面内力对比

本桥2＃～3＃板间和5＃～6＃板间的铰缝刚度按8个等级进行折减，按荷载公路I级，利用Midas/Civil有限元软件分别进行加载计算，得到各工况下1＃～8＃空心板的跨中弯矩值和位移值，见表1、表2。

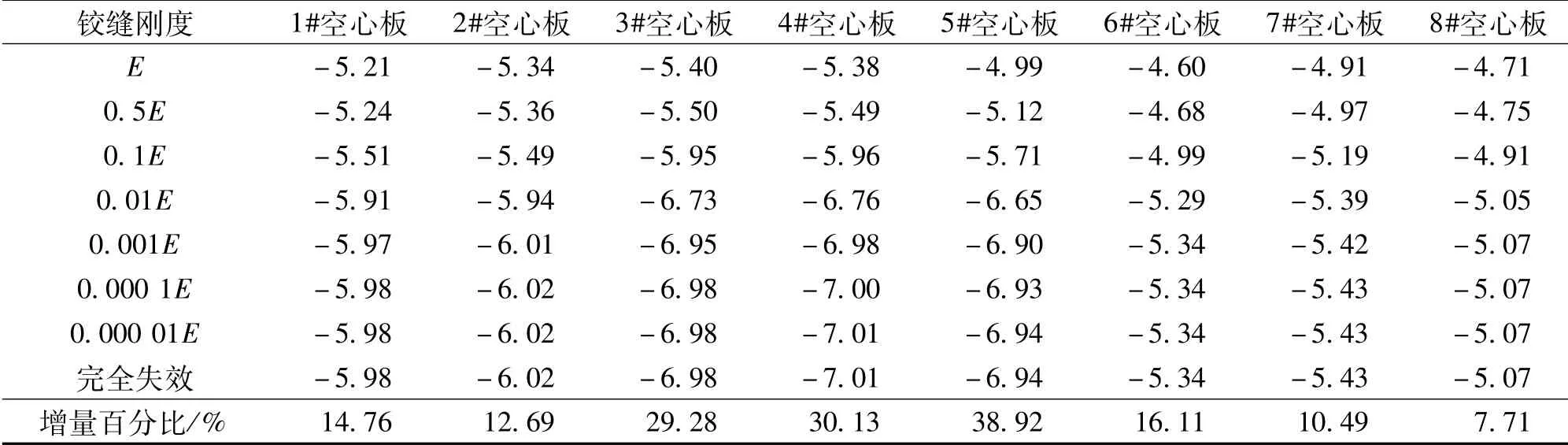
表2 铰缝刚度折减下各空心板跨中截面位置位移值 单位：mm

铰缝刚度折减后，各空心板内力进行了重分布，由表1可以看出，随着铰缝刚度的折减，3＃～5＃空心板内力值增加幅度最大，最大为33.02%，同时从图6可以看出，3＃～5＃空心板处于最不利位置。从图7中可以看出，随着铰缝刚度从0.5E到0.01E折减，各梁弯矩值有明显的增值变化。铰缝刚度折减到0.01E后，1＃～8＃梁内力值有确定的横向分布特征，不再随铰缝刚度折减发生变化；3＃～5＃空心板内力最大，1＃～2＃空心板内力次之，6＃～8＃空心板内力最小。

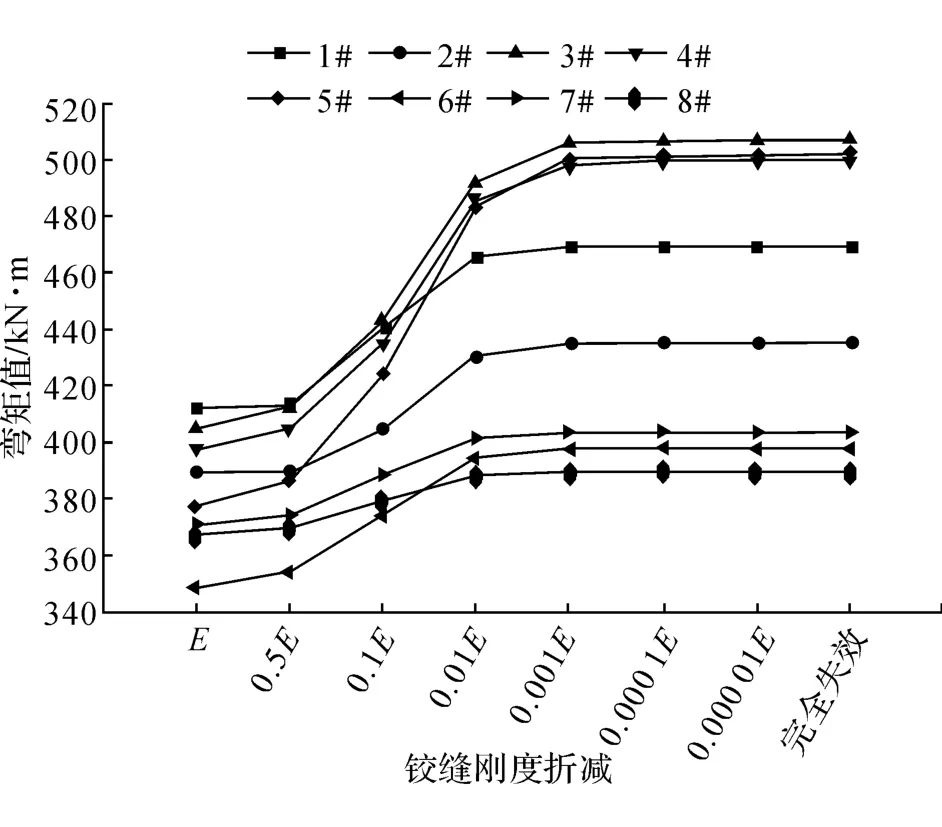
图7 各级铰缝刚度折减下空心板弯矩曲线

表1 铰缝刚度折减下各空心板跨中截面位置弯矩值 单位：kN·m

图6 偏载工况空心板模型弯矩

3.3.2 铰缝刚度折减下各空心板跨中位置截面位移对比

铰缝刚度折减后，各空心板内力进行了重分布，由表2可以看出，随着铰缝刚度的折减，3＃～5＃空心板位移值增加幅度最大，最大为38.92%，同时从图8中明显看出，3＃～5＃空心板位移值最大。从图9中可以看出，随着铰缝刚度从0.5E到0.01E折减，各梁位移值有明显的增值变化，铰缝刚度折减到0.01E后，1＃～8＃梁位移值不再随铰缝刚度折减发生变化，3＃～5＃空心板位移值最大，1＃～2＃空心板位移值次之，6＃～8＃空心板位移值最小。

图8 偏载工况空心板模型位移

3.3.3 铰缝刚度折减下各相邻空心板跨中位置位移差值百分比

从上面的分析中可知，各空心板内力值和位移值相对应，因此可以从相邻空心板位移的差值角度来分析铰缝失效程度，见图10。

图10 各级铰缝刚度折减下相邻空心板位移差值百分比

该桥梁2＃～3＃板间铰缝和5＃～6＃板间铰缝出现破坏现象，从图10中可以看出，铰缝刚度折减区间为E～0.5E时，各相邻板的位移差值没有明显变化，所以这个区间铰缝的破坏程度不影响荷载的横向传递。但随着铰缝破坏程度的增加，2＃和3＃空心板以及5＃和6＃空心板间位移差值百分比迅速增大，最大为29.8%。但荷载横向分布理论依据是铰缝相对位移为零，所以此时的铰缝已经完全失效。因此根据相邻铰缝的位移差值百分比来反映铰缝的破坏程度，从而来判定桥梁铰缝的失效状态是可行的。

4 结 语

在装配式空心板梁中，铰缝经常会因车辆荷载及冲击力的反复作用，使得铰缝发生破坏，进而影响梁板的荷载横向传递，使其分布不均匀。根据模型计算结果，当桥梁铰缝破坏程度不大时，即铰缝刚度处于E～0.5E区间，对荷载横向分布影响不大；当铰缝破坏到一定程度时，即铰缝刚度处于0.5E～0.01E区间，铰缝传力能力快速降低，荷载横向传递受较大影响，威胁到桥梁的安全。同时计算结果表明，相邻板跨中位移差值百分比与铰缝破坏程度紧密相关，可以通过比较相邻空心板的跨中位置位移的差值百分比来判断铰缝的破坏程度，进而判断桥梁的安全状况。