AutoNaut构型波浪滑翔器驱动机构数值模拟

刘刚， 桑宏强， 孙秀军

(1.天津工业大学机械工程学院， 天津 300387; 2.中国海洋大学物理海洋教育部重点实验室, 青岛 266100; 3.青岛海洋科学与技术国家实验室/海洋动力过程与气候功能实验室, 青岛 266237)

人类社会的发展与海洋有着极为密切的联系，而如何高效地开发海洋资源成为学者们研究的焦点。最有效的方式就是采用一系列无人平台进行海洋资源的探测与开采，其中就有一类无人平台通过波浪驱动或者辅助推进的方式实现前向推进运动-波浪滑翔器[1-2]。

利用波浪产生前向动力的方式有多种，较为高效常见的两种分别是利用浮体船的升沉运动产生前向动力和利用浮体船的俯仰和升沉共同运动产生前向动力。传统波浪滑翔器采用了升沉驱动方式，但是这类的驱动方式存在诸多局限性，因此AutoNaut有限公司开发了一款升沉俯仰驱动的无人平台——AutoNaut。AutoNaut只有4个活动的部件，因此结构强度非常坚固，能够执行长时间的任务。即使在恶劣海况下也能够存活，根据记载其能够在65 kn风暴条件和10 m海浪下存活。华南理工大学也设计了一款波浪驱动的无人双体船，该船通过前后水翼将船体俯仰吸收的能量转换为前向动力，表面搭载太阳能电池板提供控制能源，于2017年在珠海荷包岛海域成功进行了海试[3]。

在理论研究上，学者研究主要集中于推进系统的机理研究和参数优化。Yu等[4]建立了海洋移动浮标的动力学模型，利用数值积分法求解常微分方程，得到了平台和水翼的响应，并将方程简化，得到浮标升沉运动、弹簧刚度系数和前进速度之间的关系，结果表明随着浮标升沉运动幅值的增加，浮标的运动速度也会增加，且水翼摆角增大。Bøckmann等[5]通过实验比较了主动控制俯仰运动和被动控制的水翼所产生推力大小，结果表明被动控制的水翼能够适应自由流的变换，因此被动控制的水翼效果优于主动控制的水翼。Terao等[6]根据MermaidⅡ的波浪推进系统，进行了数值与实验分析，研究了船体的横截面形状和水翼的深度对推进力的影响，发现细长船体推进性能最佳，水翼的安装深度为水翼弦长1.5倍为最佳深度。Chang等[7]研究了波浪动力船在升沉和俯仰运动激励下的动力特性，利用了多体动力学软件ADAMS分析了不同波高、波周期和扭簧刚度系数下的推进性能，结果表明在4级海况下最佳的扭簧刚度系数为0.1 Nm/deg。邓超等[8]将波浪动力船的多体动力学方程编写到流体分析软件中进行分析，获取了静水中波浪动力船扭簧刚度系数、波浪振幅、周期和推力之间的关系。然而水翼建模时，并未考虑水质点的运动。Bowker等[9]提出了一种混合离散时域数值模型，并对波浪推进船进行了规则波自由航行试验，确定了船与水翼的耦合动力学模型，并预测了船体的前进速度。然而，未研究前后水翼之间的影响因素，而前后水翼之间的运动对其动力性能影响较为关键。

针对当前双体结构的波浪滑翔器作业水深苛刻、驱动效率不足、机动性不高和布放回收困难等不足，对这种利用俯仰和升沉共同驱动的波浪滑翔器研究是极为必要的。现从ANWG(AutoNaut architecture wave glider)运动机理层面进行深入分析，对其进行详细的结构设计，并初步进行海试实验，从实验数据中发现ANWG存在的问题，针对该问题，通过AQWA和FLUENT仿真计算，求解最佳的前后水翼刚度系数，最后通过实验验证仿真计算。

1 工作原理和结构设计

1.1 工作原理

ANWG能够通过自身的纯机械结构获得波浪动力，从而实现前向驱动，其工作原理如图1所示。在浮体船前后各有一对浸没在一定水深的水翼，水翼与固定臂通过铰链连接。浮体船随着波浪响应产生升沉和俯仰运动，与此同时，弹性水翼在水中绕浮体船中心转动，产生水平方向的推力，带动浮体船沿其运动方向前进。当波峰来临时，浮体船在波浪的激励下做抬艏和上升运动，带动前翼逆时针转动，后翼顺时针转动，水翼与水流速度V形成一定攻角αe，在升力FT和阻力FN的作用下产生一个前进方向的驱动力。当波谷来临时，浮体船在自重作用下做下摆和下降运动，带动前翼顺时针转动，后翼逆时针转动，与水流形成一定攻角，在升阻力的作用下产生一个前进方向的驱动力。

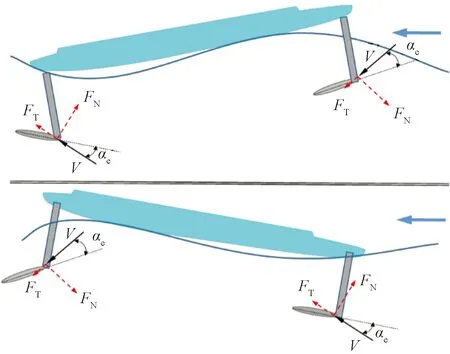
图1 ANWG的工作原理Fig.1 The working principle of the ANWG

1.2 总体结构设计

1.2.1 总体功能要求及设计目标

ANWG的概念提出是集成双体结构波浪滑翔器和波浪推进无人船二者的功能，达到取长补短的目的。ANWG的功能简单描述如下：能够在深远海完成探测任务；在河口或者码头等浅海区域，能够完成自动航行运动，实现岸边布放和回收；数据远程发送到岸基监控中心加以处理；质量轻体积小，方便携带，能够在小型船只上完成布放回收操作。ANWG设计目标为：总排水量不大于100 kg，质量不大于100 kg，负载大于50 kg，平均航速大于0.5 m/s，太阳能发电功率大于90 W，续航时间大于6个月，转向半径小于50 m，配置有电子罗盘、GPS系统等实现导航控制，配置有无线和卫星通信系统实现数据和指令的远程传输。

1.2.2 浮体船结构设计

ANGW浮体船作为波浪能获取机构，需要有足够大的浮力来增大俯仰和升沉运动的响应能力。另外一方面，较大的浮体船运动会增加水翼的响应，从而增加前向推进力，而在较低的长宽比下，波浪中的附加阻力成为主导因素，使增加浮体船运动产生的推进力受限[10]。ANWG浮体船采用长宽比为8.75，浮体船外形采用Wigley细长条船型[11]，船体截面参数y(x,z)计算公式为

(1)

式(1)中：B为浮体船宽度；T为吃水深度；x和z分别为浮体船截面的坐标点；L为船体长度。

相关文献表明，较小的水线面积可以改善ANWG在迎浪航行时的推进性能。因此，水线面积设计为1.33 m2。容积比的变化对ANWG推进性能影响不大，除非容积比的变化非常巨大，数值模拟表明迎浪和顺浪最佳的容积比约为10，但是由于有效载荷变化产生的小偏差不会对推进性能产生较大影响，为了保证ANWG整体的轻质性，将容积比设计为10。浮体船主要参数如表1所示。

表1 浮体船参数Table 1 The parameters of the float

浮体船内部骨架由316角钢和不锈钢板焊接而成，并在内部填充EVA(ethylene vinyl acetate copolymer)发泡材料，来提供足够的浮力。为了提高浮体船结构强度和使用寿命，将整条船喷覆一层聚脲。浮体船内部分为4个舱段，分别为两个控制舱、一个电池舱和一个传感器舱。浮体船甲板搭载三块功率分别为30 W的太阳能电池板，给控制舱及传感器舱提供能源，并将多余的能量存储至电池包内。此外，甲板还可搭载北斗、气象站、温湿度等传感器，船底可搭载ADCP(acoustic doppler current profiler)等传感器。其总体结构如图2所示。

图2 ANWG总体结构Fig.2 The overall structure of the ANWG

ANWG转向尾舵采用了磁耦合传动，其高效的动力性使得浮体船具有良好的稳定性和转向性。为提高尾舵的水动力性能，采用NACA0012系列翼型。结合中外研究经验，选取尾舵板的弦长为0.15 m，展长为0.28 m，舵面积为0.453 m2。通过分析发现，当转轴安装在距离前缘位置0.25倍弦长时，各个攻角下的铰链力矩系数都保持在较小的值[12]。根据Andera的模拟数据显示，水翼的动力性能随着前后水翼的间距增加而不断增加，当水翼之间的间距为船体长度的110%时，水翼的推力能够达到最大[13]。因此，根据实际情况，将前后水翼的间距设定为90%的船体长度，此时与110%船体长度的距离相比，其动力性能减少不多，但是对整体结构的可靠性提升较大。

1.2.3 波浪动力转换机构设计

波浪动力转换机构按照工作原理可分为主动形式和被动形式两种[14]。主动形式的动力转换机构优点在于能够适应于不同海况，根据实时回传数据对水翼的摆动角度进行调整。被动形式的动力转换机构采用了弹性储能机构，通过预先调节至合适的弹簧刚度系数，从而使水翼在浮体船及波浪共同作用下自由摆动产生推进力，拥有更强的适应性。而且，这种结构更为简洁，成本更加低廉，且可靠性也较高。

波浪动力转换机构如图3所示，结构主梁为两块316不锈钢板，内部安装一根超弹性的镍钛合金丝。镍钛合金丝有着良好的弹性性能，而且具有耐磨性、高阻尼、抗腐蚀等优异的特点[15]。在不锈钢板外侧加装一对NACA0012水翼，水翼转轴位于前缘40 mm处，直径3 mm的镍钛合金丝下端穿过水翼转轴并与转轴固定，上端穿过一个滑块，滑块可在两块不锈钢板间自由滑动，并可通过不锈钢板上的锯齿槽固定。当水翼转动时，镍钛合金丝会弯曲，从而产生一个扭矩，试图将水翼扭转到平衡位置。通过调节滑块与水翼转轴之间的距离，可以改变镍钛合金丝的弯曲长度，从而调节整套机构的弹簧刚度系数。

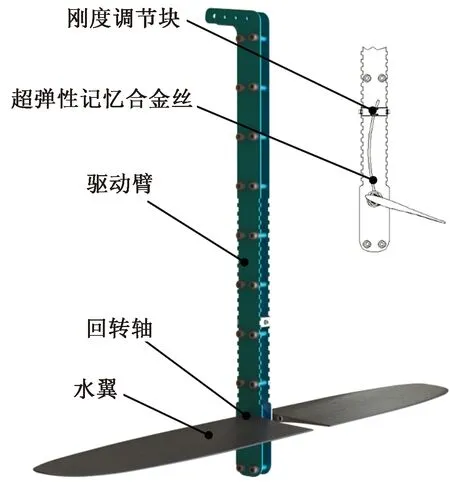
图3 波浪动力转换机构三维模型及原理Fig.3 Three dimensional model and principle of wave power conversion mechanism

镍钛合金丝转换为弹簧扭矩的原理简化图如图4所示，理论的弹簧刚度系数采用经典梁理论，并且假设系统中的摩擦力为0，可以求解得到角度与扭矩对应的关系为

图4 镍钛合金丝刚度转换简化图Fig.4 Simplified diagram of stiffness conversion of NiTi alloy wire

(2)

(3)

式中：θA为A点转动的角度；M为转动产生的扭矩；l1为镍钛合金丝弯曲长度；E为弹性模量；d为镍钛合金丝直径。

波浪动力转换机构主梁钢板上划分为20小格，每格距离为15 mm。以每4格做一个标记点，距离水翼转轴处为1号标记点，最远处为5号标记点，然后通过施加力矩形式来测量翼板摆动角度与弹簧刚度系数的关系。将波浪动力转换机构垂直安装在工作台上，将砝码垂吊在波浪动力转换机构第二根转轴处(距离水翼回转轴40 mm)，不断增加砝码，水翼转轴发生转动，通过固定于水翼平面上的WT901姿态传感器获取水翼转角，最后经过换算，得到弹簧的刚度系数，测量结果如表2所示。从表2中可以看出测量结果与理论计算值较为接近，数值的偏差来源于机构之间的摩擦力，但是在可接受范围。

表2 动力转换机构理论弹簧刚度系数与测量值Table2 Theoretical spring stiffness coefficients and measured values of wave power conversion mechanism

2 ANWG海试实验及结果分析

2.1 ANWG近海自航行实验

海试实验将ANWG波浪动力转换机构弹簧刚度系数调节至6 (N·m)/rad。在浮体船质心位置和前后水翼质心位置安装WT901姿态传感器，以5 Hz频率同步采集三者的姿态数据和加速度数据。波浪滑翔器航向由船尾罗盘以0.5 Hz频率进行控制，浮体船的速度由GPS数据求解而来，采样频率为5 Hz。

2021年1月31日上午9点，将海试设备运载至青岛大管岛海域。实验轨迹为AB两点直线拉距，目标点A坐标为120°42′24.74″E、36°12′49.72″N；目标点B坐标为120°43′1.74″E、36°11′16.02″N。海试过程和路径如图5所示。

图5 ANWG海试过程和路径Fig.5 ANWG sea trial process and path

2.2 实验结果及存在的问题

ANWG自航行实验的速度曲线如图6(a)所示，从图6(a)中可以看出，设备平均速度为0.156 m/s，最小速度为0.039 m/s，最大速度为0.52 m/s。ANWG浮体船和前后水翼的部分姿态数据如图6(b)所示，从图6(b)中可以看出，浮体船俯仰角度为±3°，前水翼摆角范围为-30°～8°，后水翼摆角范围为-10°～20°，水翼俯仰角度呈周期性变化。

图6 ANWG海试速度及姿态Fig.6 ANWG sea trial velocities and attitudes

可以看出，实验的结果与设计目标有一定的差距，进一步对其运动机理进行分析，探究影响航行速度的因素。实验设定前后水翼弹簧刚度系数均为6 (N·m)/rad，但是从图中可以看出，前后水翼的摆角并不一致，前水翼摆角始终大于后水翼的摆角。这种现象产生的原因是在自航行过程中，ANWG始终处于逆浪航向状态。逆浪航行时，前水翼的运动会更加剧烈，从而使其摆角增加。俯仰运动引起的升沉方向变化与浮体船升沉同步，从而增加了前水翼的相对运动幅值，也能进一步提高前水翼的推进力大小。而后水翼则呈现出负叠加状态，减小了水翼的相对运动幅值。综上所述，前水翼相对运动幅值要大于后水翼相对运动幅值，因此在此次自航行实验中，前水翼的推力要大于后水翼的推力。其次，在自航行实验中，前后水翼的摆角相位差小于90°，极大的影响了其水动力的获取。

因此，针对以上问题对ANWG进行改进，通过理论分析和仿真计算探究其前后水翼的最佳弹簧刚度系数，使其前后水翼推力最大，提高ANWG航行速度。

3 ANWG运动响应分析

3.1 浮体船和前后水翼运动分析

波浪动力转换机构刚性连接在浮体船前后部分，需要先将浮体船质心处的运动转换为动力转换机构处的运动。在波浪的作用下，水翼会产生以下三种运动：水翼绕自身回转轴的旋转运动θf1和θf2、水翼质心绕浮体船质心的旋转运动η5和在水翼随着浮体船上下起伏的运动yf1和yf2，其运动示意图如图7所示。

vw为水质点在y方向的运动；η3为浮体船的升沉运动； xf为水翼与船体质心在船长方向的距离；下标1 表示前水翼；下标2表示后水翼图7 浮体船和前后水翼运动Fig.7 The movement of the float, aft and forward hydrofoils

将水翼质心绕浮体船质心的旋转运动进行分解，分解成x方向和y方向的运动，由于浮体船的俯仰角度较小，且水翼距离浮体船质心较远，x方向的运动可以忽略不计，仅仅考虑y方向的运动。因此，水翼质心的运动表示为

(4)

(5)

式中：φ为前后水翼运动相位差；df为水翼支架长度。

波浪是一种振荡波，其内部水质点会围绕自身的平衡位置做圆周运动[16]。自由面上的圆半径最大，等于波浪波幅，随着水深的不断增加，振荡圆的半径急速减小。根据有限水深微波理论，可以确定不同水深下水质点的运动速度，水质点在y方向上的运动[17]可以表示为

vw=ωAekzcos(ωt-kx)

(6)

式(6)中：vw为水质点在y方向上的运动；ω为波频；A为波幅；k为波数，通过公式k=2π/λ求解；λ为波长。

前后水翼的速度最终可以通过其自身速度与水质点速度进行叠加得到。

ωAekzcos(ωt-kx)

(7)

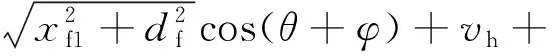
ωAekzcos(ωt-kx)

(8)

3.2 仿真设置

ANWG在波浪中前行时，会进行六自由度的摇荡运动。主要探究ANWG的纵向运动性能，因此只需考虑对其运动性能影响最大的升沉和俯仰运动。采用了ANSYS-AQWA软件对ANWG浮体船进行动态响应分析，分别通过在频域和时域中计算，获取浮体船的RAOs(response amplitude operators)和随着时间变化的升沉俯仰运动数值。

图8 ANWG在AQWA中的网格划分Fig.8 The meshing of the ANWG in AQWA

图9 浮体船在不同速度、波频下的附加质量和阻尼系数Fig.9 Added masses and damping coefficients of the float under different speeds and wave frequencies

由于所研究波频范围在0.1～1 Hz，因此选择设置最小网格尺寸为0.01 m，网格数量为18 771， ANWG在AQWA中的网格划分如图8所示。定义水深为20 m，重力加速度为-9.81 m/s2，浮体船排水量为80 kg。重心位置相对于基面线为40 mm，重量分布是对称分布，所以重心横向坐标为0。浮体船惯性矩通过SolidWorks获取为Ixx=10.993 kg·m2，Iyy=91.84 kg·m2，Izz=84.59 kg·m2。

3.3 浮体船水动力参数获取

通过频域分析，可以获得浮体船在不同波频下的附加质量和阻尼系数。给定浮体船一个初始速度，对其在不同波频下的水动力参数进行仿真计算，浮体船在不同速度、波频下的附加质量和阻尼系数如图9所示。由于本文重点研究ANWG在纵平面内的运动，因此只需获取相关的附加质量和阻尼系数。将附加质量和阻尼系数拟合成方程，后续建立水翼数值模型计算时，将其带入UDF函数中进行水翼的推力求解。

4 前后水翼水动力仿真

4.1 水翼数值计算模型及参数设置

对二维水翼进行计算域的选择，既要保证能够使水翼达到稳态的运动状态，又要保证计算域不至于过大导致网格数量变大，引起计算量过大，从而浪费了计算机的资源。本文研究对水翼前向航行性能进行数值仿真，因此将计算域设置成长方形，以水翼的特征弦长c为测量尺度，则整个水池的长度为100c，宽为20c。计算域右侧设置压力入口，左侧设置压力出口，上下边界设置为壁面边界，水翼设置为壁面边界，水翼距离压力出口为10c，距离上下壁面边界为10c。水翼质心与壁面的距离始终大于5c，以此来减小计算域壁面对扑动水翼运动的影响，如图10所示。

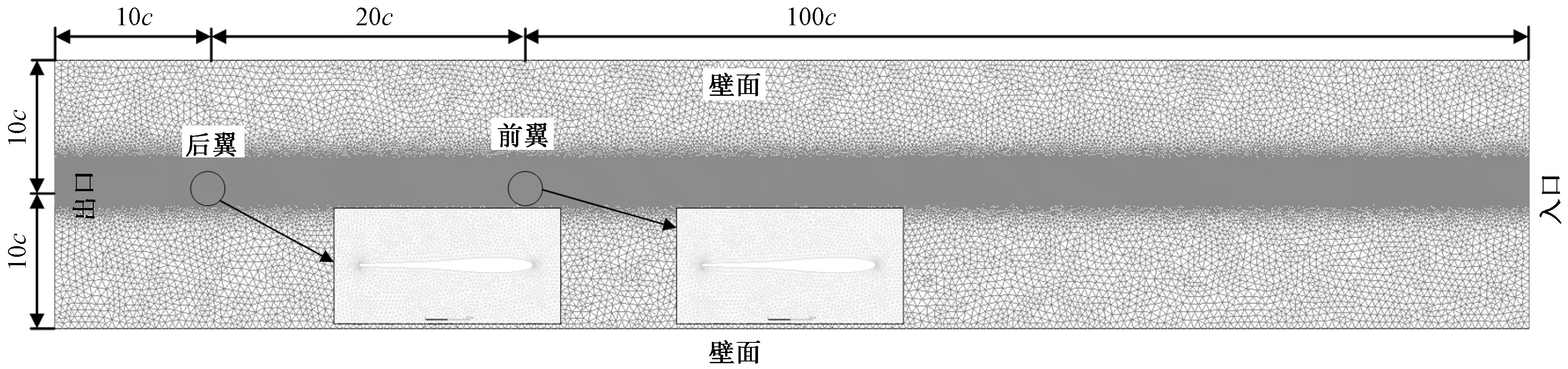
图10 计算域和网格Fig.10 Computing domain and grid

采用SSTk-ω模型，并采用动网格结构，根据水翼的运动状态和特点，在设置上同时设定了弹簧光顺方法和局部重构方法，让网格始终保持较高的质量。根据ANWG航行的海域，设定仿真将在波频0.3 Hz条件下进行，波高为0.4 m。针对ANWG的初步海试结果及理论分析，分别将前后水翼的弹簧刚度系数设定为2、4、6、8、10(N·m)/rad。通过AQWA软件获取了ANWG浮体船的运动响应，来确定水翼的运动控制方程。并将其应用于FLUENT仿真计算，通过UDF用户自定义函数控制其运动[18-19]，将水翼的运动控制方程、水翼的受力方程和总体阻力方程进行数值迭代求解，能够得到水翼被动扑动的运动状态，最后将水翼摆角和水平推力等计算数值进行输出。

4.2 网格无关性验证

为了研究求解器网格的依赖性，选取三种网格进行对比验证，网格数量分别是320万(精细)，136万(中等)和46万(粗糙)，网格细化因子大于1.3。网格无关性验证仿真条件为：NACA0012水翼水平放置，入射角为0°，来流速度为1.5 m/s，并监测水翼的升力和阻力。通过计算得到了网格无关性的验证参数，如表3所示。可以发现，GCI(grid convergence index)值较低，收敛性较好。因此，最终选取136万网格进行仿真计算。

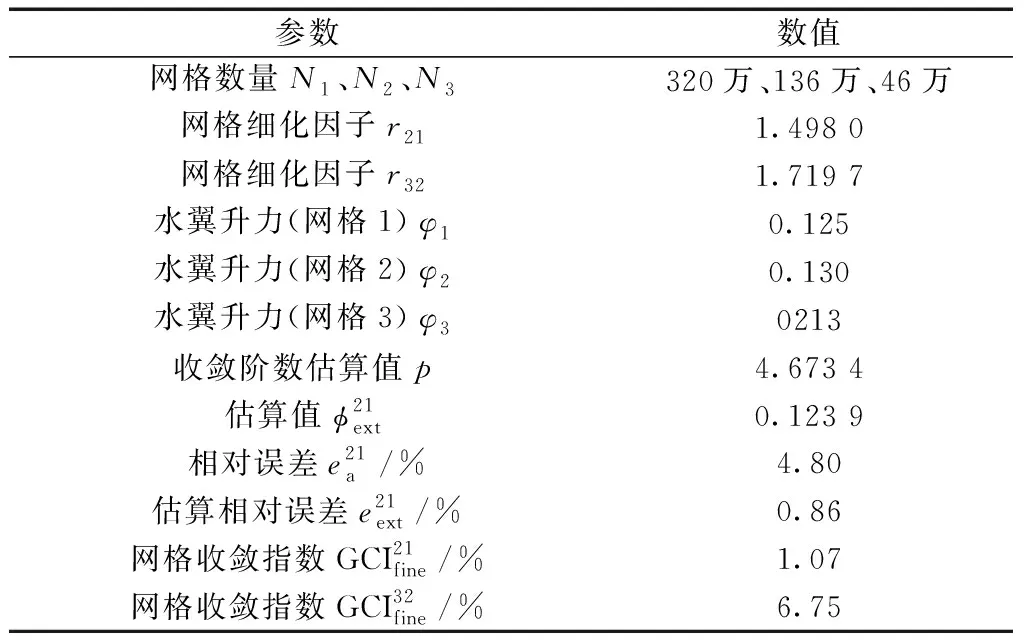
表3 网格数量及无关性验证参数Table 3 The verification parameters of grid number and independence verification parameters

4.3 仿真结果分析

对不同前后弹簧刚度系数下的水翼进行仿真计算，分别得到了水翼的前向推进力大小，取平均值得到网格曲线，如图11所示。由于水翼不能时刻保持为最佳攻角状态，且为了保证与海试结果的一致性，将ANWG的总体阻力加入到了仿真中，因此水翼的推力大小会产生负值。从图中可以看到，前后水翼不同弹簧刚度系数下，对ANWG推力影响极大。前后水翼弹簧刚度系数较大或者较小产生的推力都较小，而且前后水翼取同一弹簧刚度系数也并没有达到最佳的推力。当前翼弹簧刚度系数为4 (N·m)/rad，后翼弹簧刚度系数为6 (N·m)/rad时，前后水翼所产生的前向推力达到最大值，此时推力为7.9 N，因此，对于0.3 Hz波频和0.4 m波高海况下，ANWG最佳的弹簧刚度系数组合为前翼4 (N·m)/rad，后翼6 (N·m)/rad。

图11 ANWG前后水翼不同弹簧刚度系数下平均推力Fig.11 Average thrusts under different spring stiffness coefficients of the forward and aft hydrofoils of the ANWG

前后水翼摆角曲线如图12所示，从图12中可以看到，前后水翼摆角大小较为一致，这表明了刚度系数的选择较为准确。前后水翼的摆角在±20°，相位差约为90°，这与之前的研究较为一致。

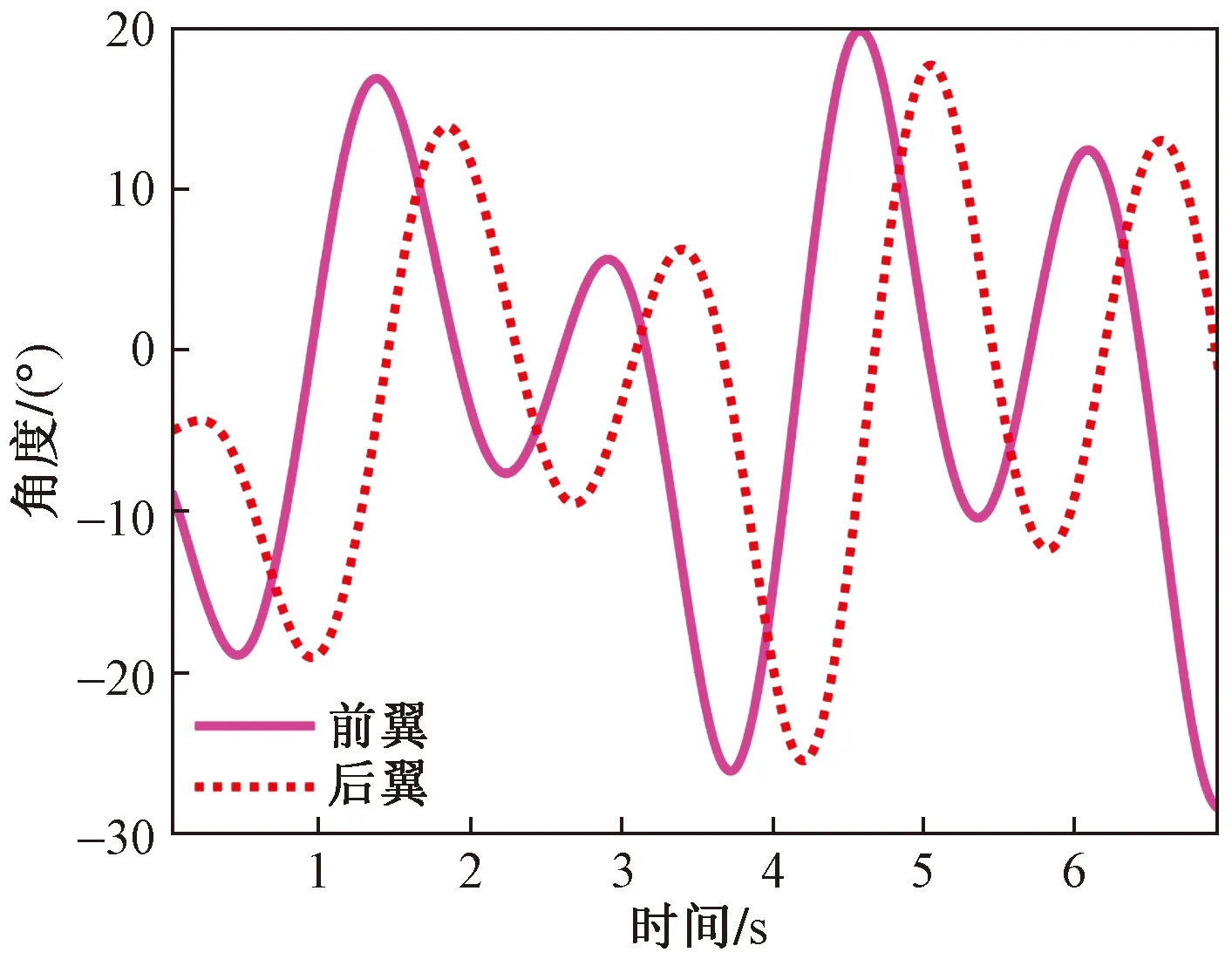
图12 ANWG前后水翼摆角Fig.12 The flapping angles of the forward and aft hydrofoils of the ANWG

5 ANWG改进实验验证

为了保证实验的有效性和数据的准确性，尽量排除环境的影响因素，海试地点与上述实验一致，轨迹点为AB两点，坐标与上述实验一致，A点坐标为：120°42′24.74″E、36°12′49.72″N；B坐标为：120°43′1.74″E、36°11′16.02″N。海试时间为2021年5月16日10:00开始，并于18:00结束。实验设备与上述实验保持一致，将前翼弹簧刚度系数调整为4 (N·m)/rad，后翼弹簧刚度系数调整为6 (N·m)/rad。

图13 ANWG海试速度及姿态Fig.13 ANWG sea trial velocities and attitudes

改进后的ANWG海试实验数据如图13所示，其中图13(a)为自航行速度曲线，图13(b)为前后水翼和浮体船姿态曲线。从图13中可以看出，改进后ANWG的速度有较为明显的提升，峰值速度达到了0.7 m/s，平均速度为0.465 m/s，较第一次实验提升了，基本达到了设计要求。而且从姿态曲线可以看出，经过前后水翼弹簧刚度系数的调整之后，前后水翼的运动曲线都较为一致，这与仿真结果较为吻合。

6 结论

基于双体结构波浪滑翔器存在诸多不足之处，设计了一款AutoNaut构型波浪滑翔器，并针对初步海试实验中发现的前后水翼扑动角度异常等问题，通过AQWA和FLUENT针对问题进行改进，最后通过海试实验验证了仿真结果。

(1)从总体到局部进行了ANWG总体结构设计，设计了一款弹簧刚度系数可调波浪动力转换机构，并对其中超弹性镍钛合金丝转换出来的弹簧刚度系数进行划分和校准。

(2)针对海试中的问题，在考虑水质点运动基础上，求解了前后水翼运动方程，并通过AQWA计算了ANWG的附加质量和阻尼系数，为水翼的仿真奠定基础。

(3)建立了基于浮体船运动响应的水翼被动扑动数值模型，通过仿真计算，对不同弹簧刚度系数下前后水翼进行仿真计算，求解出了最佳的弹簧刚度系数组合，最后通过海试实验，验证了该方案的可行性。