基于多频段图模型的微弱脑电信号异常检测

贺光硕，卢国梁*，尚伟

(1.山东大学机械工程学院，济南 250061;2.山东大学高效洁净机械制造教育部重点实验室，济南 250061；3.山东大学机械工程国家级实验教学示范中心，济南 250061；4.山东大学第二医院，济南 250033)

脑电图(electroencephalogram，EEG)包含丰富的生理和疾病信息，在临床医学领域具有广泛的应用[1]。EEG信号的分析和处理能够为某些神经性疾病如癫痫[2]、急性脑血管病[3]、脑梗死[4]等疾病的早期预警和诊断提供相关依据。其主要技术手段是对脑电信号的状态变化进行监测，即实时检测脑电信号由正常状态变为异常的过程[5]。

脑电信号动态变化的异常检测是近几十年来在脑电信号处理领域的重要研究课题，其流程主要包括：信号预处理、动态建模、决策制定[6]。其中关键的一步是对脑电信号进行动态建模，并提取一个能够表征脑电信号动态特性的综合性指标。然而，由其他生理信号和外界噪声引起脑电信号的非平稳、非线性和高变性等特点极大地影响了综合性指标的提取过程[7]。因此传统的线性指标如均值(mean)、方差(variance)、均方根(root mean square,RMS)和峰度(kurtosis)等极易受脑电信号高度复杂性的影响而产生各种误报[8]。随着脑电信号处理方法的研究，非线性指标的发展克服了传统指标的不足，受到研究者的青睐[9-10]。图模型(graph model，GM)作为一种谱分析算法，是一种独特的非线性指标，能够捕捉数据中隐藏的结构和拓扑信息，已被用于脑电信号分析[11]。Zhang等[12]利用图模型的结构信息来表示脑电传感器的空间特征，然后进行运动意图检测。Song等[13]使用图模型建模并提取多通道脑电信号的特征用来进行脑电信号的情绪识别。Haddad等[14]根据图建模描述了每个病人的发作特征，从而预测癫痫发作。

虽然动态建模方法发展迅速，但一个不可回避且尚未完全解决的问题是如何检测给定脑电信号中的微弱的异常变化，目前的方法在脑电信号微弱异常变化检测方面效果不佳。检测微弱变化能够提前预测和诊断癫痫发作等神经疾病，从而为医生的治疗做好提前准备，在临床应用中具有重大意义[10]。

在脑电信号的处理过程中，通常把脑电信号发生异常变化的频段分为δ、θ、α、β和 γ波，不同的频率段包含不同的疾病信息和原始信号信息[15]。虽然现有的GM动态建模方法对噪声具有很强的鲁棒性，但在处理脑电信号的微弱异常变化时仍有很大的局限性。

针对以上问题，现提出一种基于多频段图模型的脑电信号微弱异常检测方法。采用GM对δ、θ、α、β和 γ 5个频段分别进行建模来增强的脑电微弱变化信息，并提取各个频段脑电信号的特征，采用自适应权重融合算法融合频段特征，生成综合性指标用来描述脑电信号的动态变化，以期解决脑电信号中微弱异常变化的检测准确率低的问题。

1 实验数据来源

1.1 脑电数据库的选取

所用数据库选自公开的CHB-MIT头皮EEG数据库[16](网址：https://physionet.org/content /chbmit/1.0.0/)和来自山东大学第二医院神经内科的EEG数据库[11,17]。

1.1.1 CHB-MIT头皮EEG数据库

该数据库由患有难治性癫痫病的儿科受试者的脑电图数据记录组成，收集了22名受试者共24个案例，采样率为256 Hz。每个案例(chb01、chb02等)包含来自一名受试者的9～42个连续.edf文件并且大多数文件的时间跨度为1 h。如图1所示，每个案例详细地标注了癫痫发作的时间和次数，方便了实验时对异常变化点的标注。在每种案例中，随机选择一个含有癫痫发作的.edf文件作为测试数据，共24个数据，选择第16个通道数据作为实验所需的测试数据。

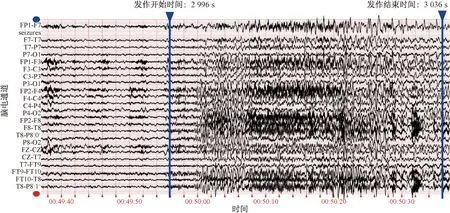
图1 原始脑电信号癫痫发作时间(以chb01_03为例)Fig.1 Raw EEG signal seizure time(take chb01_03 as an example)

1.1.2 山东大学第二医院神经内科EEG数据库

该数据库的所有EEG数据均来自癫痫患者，且所有受试者均已获得书面知情同意。该实验完全遵守《赫尔辛基宣言》和当地相关法律法规。实验所用的癫痫检测系统用于监测夜间睡眠中的癫痫[17]，同时收集受试者的EEG数据和相应的监控视频。

原始脑电信号以1 024 Hz的采样率记录，并在进一步分析之前降采样为512 Hz。该数据集包含32通道的脑电信号，随机选取其中的C3通道为测试数据，共包含55个数据序列。由于癫痫发作时脑电信号的变化非常微弱，很难用肉眼直接判断是否变化。因此，具有丰富临床经验的神经科医生同时观看监控视频和所有通道的数据，来标记EEG的异常变化位置。

1.2 数据的预处理

癫痫等神经源性疾病的频率成分主要出现在δ、θ、α、β和 γ频段[15,18]。在神经性疾病发作时，这些频率的幅值会相应改变。因此，根据以上5个频段的频率定义一个0.1～70 Hz的带通滤波器来捕获该频率的脑电信号。此外，使用特定的陷波滤波器来消除50 Hz的电力线的干扰。

根据带通滤波器的截止频率和脑电信号实际异常变化情况，脑电信号各个波段频率范围为：δ波(0.1～4 Hz)、θ波(4～8 Hz)、α波(8～12 Hz)、β波(12～30 Hz)、γ波(31～70 Hz)。对于一段给定的滤波后的脑电信号，分别进行5个频段的提取，如图2所示。可以看出，脑电信号的5个频段在异常变化检测中具有不同表现，如α、β和 γ频段在异常变化位置反应明显，而δ和θ频段则无明显变化，因此所提算法对于脑电信号的微弱异常变化检测具有重要意义。

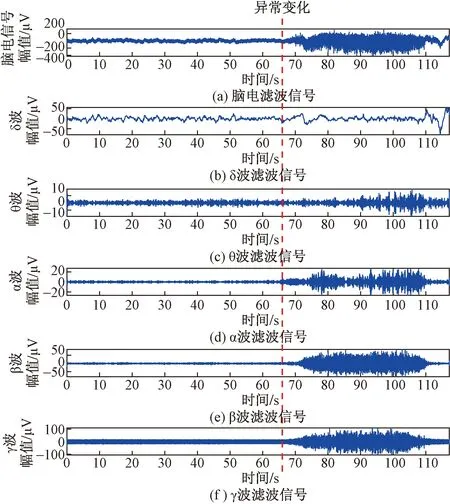
图2 原始脑电信号5个频段的滤波信号Fig.2 Filtered signals of the five frequency bands of the raw EEG signal

2 实验方法

基于多频段图模型方法，提出了脑电信号异常检测框架，步骤如下。

步骤1构造图模型：对脑电信号的5个频段(即δ、θ、α、β和 γ波)分别进行GM动态建模。

步骤2相似性分数：对每个频段的GM 运用距离函数得到能够量化GM之间关系的相似性分数。

步骤3自适应权重融合算法：利用自适应权重融合算法融合所有频段的相似性分数并最终得到一项综合性指标用来描述脑电信号的动态变化。

步骤4假设检验：最后采用假设检验来检测脑电信号是否存在微弱的异常变化。

针对一段数据，若检测到异常变化，该框架将向用户报告一个异常变化警报，然后继续一个新的检测过程。若没有检测到变化，该框架就会一直运行下去，直到数据运行结束。

2.1 构造图模型

对5个频段中每个频段分别进行构造图模型，在1.2节收集的滤波后的脑电信号中，假定δ波的脑电信号为Xδ={Xδ(t)},t=1,2,…,N，其中Xδ(t)为t时刻的观测值。

构造图模型的过程如下。

步骤1利用离散短时傅里叶变换(discrete short time Fourier transform,DSTFT)将信号从时域转换到频域。当窗口长度固定时，DSTFT的计算公式为

(1)

式(1)中:φ*(·)为窗口函数；p为DSTFT得到的频率数据；i=1,2,…,N/2；j为虚数；N为窗口函数移动的时间步长，N=512；m为第m个时间步长。

步骤2计算功率谱，通过式(2)可以得到一系列周期图P。

(2)

步骤3周期图P(i,m)用于定义时间t处的频率分辨率，即Fm={f(i)},i=1,2,…,N/2。其中，f(i)为频率，Fm为频率f(i)的集合。将每个频率分辨率视为一个节点，计算每两个节点之间的欧氏距离di,j作为边的权重。

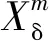
(3)

2.2 相似性分数

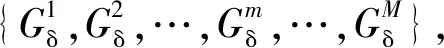
(4)

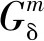
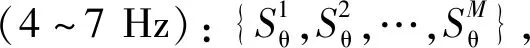
对图2中信号的5个频段进行以上步骤分析，得到相似性分数如图3所示。可以看出，θ波的相似性分数在异常变化位置没有明显变化，其他波段相似性分数变化较为明显，主要原因是脑电信号的变化信息隐藏在不同的频率成分中。因此，为了充分利用这些重要的微弱变化信息来实现对EEG信号的自适应检测，需要一种自适应权重融合算法对所有的相似性分数进行加权融合。

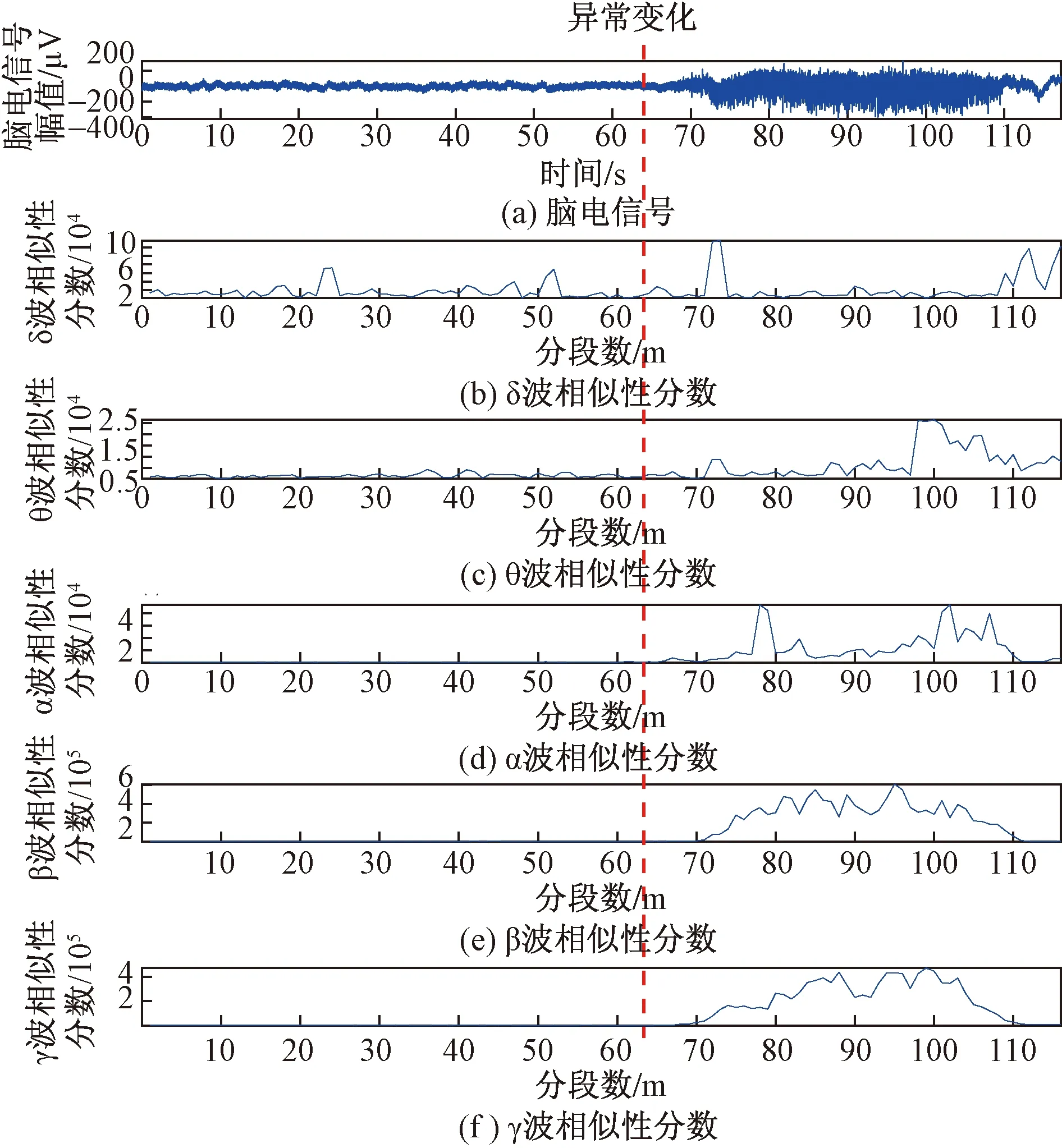
图3 相似性分数计算示例Fig.3 Example of calculation of the similarity scores

2.3 自适应权重融合算法

自适应权重通过依据各个分量的重要性自适应地计算权重，将所有相似性分数组合在一起。计算过程如下。

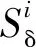
(5)

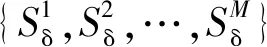
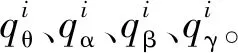
步骤2计算方差，其计算公式为

(6)

步骤3使用方差自适应地计算每个分量的权重wk，其计算公式为

(7)

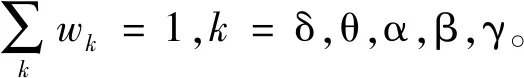
步骤4所有频段的相似性分数可表示为综合性指标Qi，其计算公式为

(8)

2.4 假设检验

基于综合性指标{Q1,Q2,…,Qm,…,QM}，采用常零假设检验进行变化决策。对于第m段，假设检验如下：H0:没发生变化，Qm∈Α；H1:发生变化，Qm∉Α，其中，Α=[μm-1-3σm-1,μm-1+3σm-1]为由常用的3σ准则定义的置信区间，其中μm-1和σm-1分别为前m-1个片段综合性指标的平均值和标准差。

图4给出了检测结果的示例。可以看出，使用的假设检验可以成功地检测出异常发生的时间，证明了所提出的综合性指标的有效性。

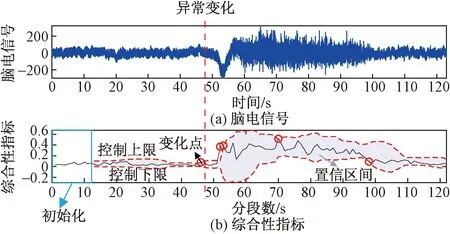
圆圈表示测试方法产生的异常变化点图4 检测结果示例Fig.4 Example of detection result

3 实验结果及讨论

两个不同数据集的实验结果，与传统线性指标如均值(mean)、方差(variance)、均方根(root mean square,RMS)和峰度(kurtosis)以及典型的非线性指标经验模态分解(empirical mode decomposition,EMD)、短时傅里叶变换(short-time fourier transform,STFT)、连续小波变换(continuous wavelet transform,CWT)和离散小波变换(discrete wavelet transform,DWT)进行了比较。采用常用指标查准率Precision、查全率Recall和F分数Fscore来评价以上方法的检测性能，定义为

(9)

(10)

(11)

式中：TP为真正例，表示正确的检测结果；FP为假正例，表示错误的检测结果；FN为假负例，表示没有检测结果。

显然，高查准率表示高检测精度，高查全率表示高检测灵敏度，F分数对检测的方法进行综合评价。

3.1 CHB-MIT头皮EEG数据库

由于CHB-MIT头皮EEG数据库脑电信号的数据量过于庞大，只截取癫痫发作开始时间点的前60 s及后60 s作为实验数据。图5展示了所提方法用于测试CHB-MIT头皮EEG数据库实验结果的示例。

显然，所提方法综合性指标能够及时检测到脑电信号的微弱变化。由图5可知，DWT有误报点，EMD和STFT未能成功检测到异常变化点，其余方法均表现良好的检测结果,但是并不能通过此例证明其他方法比综合性指标方法好。如表1所示，综合性指标在查准率、查全率和F分数之间取得的效果最好，表现出了该方法的优越性。尽管方差在查全率方面效果为100%，但是它的查准率和F分数没有综合性指标的性能要好，这也并不能说明方差在检测性能上好于综合性指标。

表1 CHB-MIT数据库检测结果进行了3个指标的比较Table 1 Comprehensive comparison in CHB-MIT scalp EEG database with three indicators

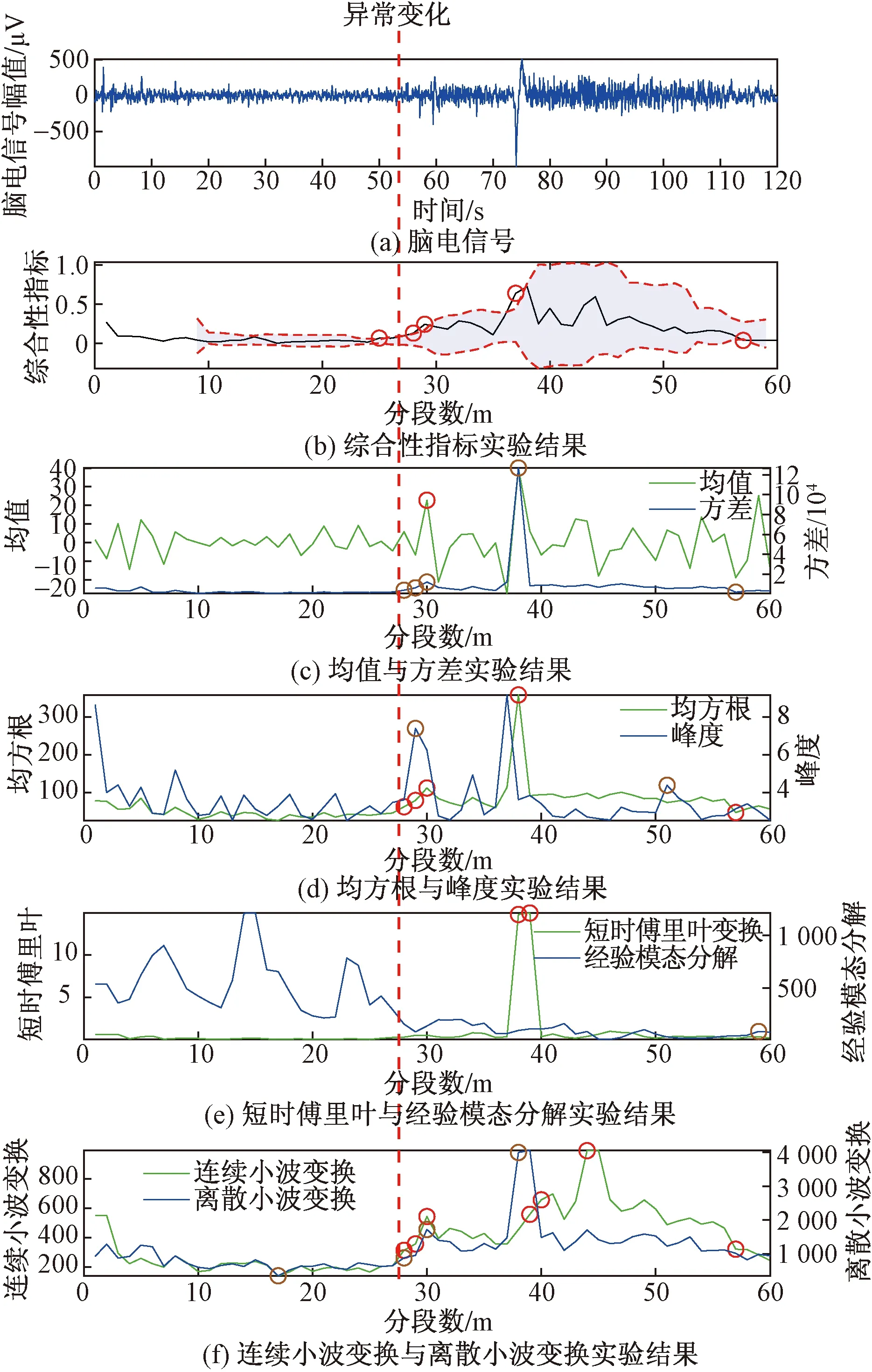
圆圈表示测试方法产生的异常变化点图5 综合性指标与其他方法的比较结果Fig.5 Comparison results of comprehensive indicators and other methods

3.2 山东大学第二医院神经内科EEG数据库

图6展示了所提方法用于测试山东大学第二医院神经内科EEG数据库实验结果的两个示例。本实验中测试数据的变化类型主要是幅值变化和频率变化。图6中测试数据1的异常变化主要是由幅值变化引起的。可以看出，除了均值、峰度和经验模态分解方法产生了误报点，其余方法都能及时检测到脑电数据的微弱异常变化。

检测由频率变化引起的脑电数据异常更具有挑战性。如图6(b)所示，很难从原始脑电信号中用肉眼直观地识别脑电信号的微弱异常变化。经过实验，只有综合性指标能够及时检测到脑电信号微弱的异常变化，其他方法均产生延迟或误报点。表2中的综合比较结果验证了这一点，只有综合性指标在查准率、查全率和F分数之间取得了最好的效果，并且查全率的结果为100%，这意味着该方法能够检测出所有潜在的脑电信号异常变化。脑电信号的非线性、非平稳性和高变性使其极容易受外界影响，极大地增加了信号的异常检测难度，所以综合性指标在查准率方面未能达到百分之百也是有情可原。基于以上结果，综合性指标具有很高的检测精度和灵敏度，并且能够准确反映脑电信号的动态变化。

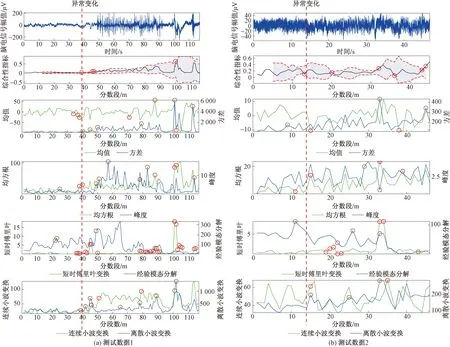
圆圈表示测试方法产生的异常变化点图6 山东大学数据集实验结果比较Fig.6 Comparison of experimental results of Shandong University data set

表2 山东大学数据集检测结果中三个指标的比较Table 2 Comprehensive comparison in Shandong University data set with three indicators

3.3 计算效率

在设计一个实用的变化检测系统时，计算效率是一个需要考虑的重要问题。综合性指标与其他比较方法的检测步骤基本一样，均包括数据建模、指标提取和决策3个阶段。表3给出了综合性指标与其他方法的计算复杂度的比较结果。结果表明，在所有的方法中，决策的计算复杂度是相同的，但在其他两个阶段的计算复杂度却有很大的不同。显然，综合性指标的总计算复杂度是最大的，这意味着随着脑电数据量的增加，该方法所消耗的时间也会大量增加。因此，在将来的工作中会进一步提高综合性指标的计算效率，增加其实用价值。

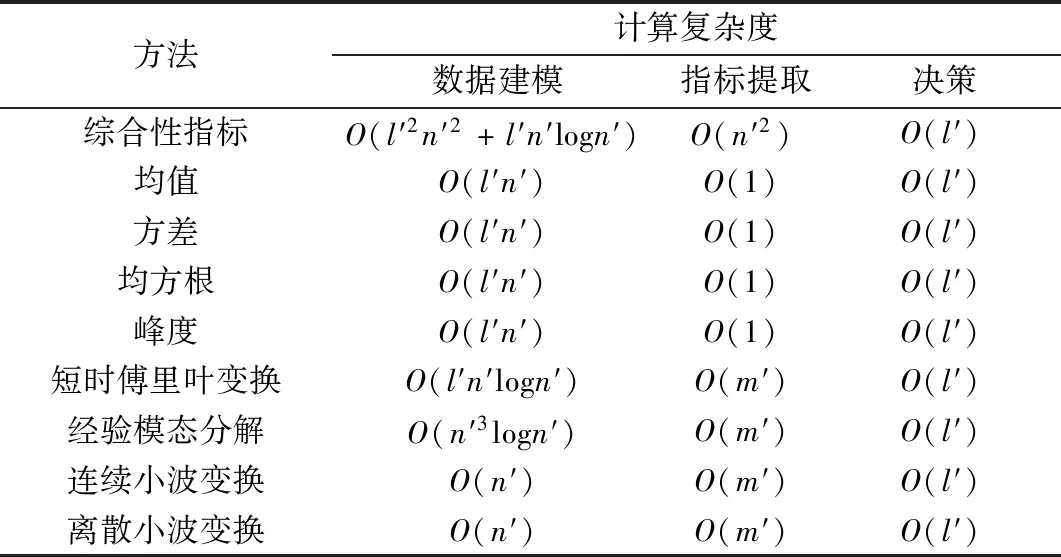
表3 计算复杂度的比较Table 3 Comparison of the computational complexity

4 结论

提出了一种基于多频段图模型的脑电信号微弱异常变化检测新方法。该方法充分利用这五个频段中脑电的微弱变化信息和GM的优势，对脑电信号δ、θ、α、β和 γ波的每个频段单独进行图模型建模，并通过自适应权重融合算法融合各图模型的相似性分数形成综合性指标进行假设检验。两个实验结果表明，所提方法查全率结果均为100%，表明所提方法能够检测所有潜在的脑电信号异常变化，因此该结果对脑电信号的微弱异常变化的检测及实际应用具有重要意义。由于所提方法的计算复杂度较高，下一步会对所提方法进一步改进以提高其计算效率，增加其应用价值。