广义变分模式分解降噪在齿轮早期故障诊断中的应用
郭燕飞, 王清华, 陈高华
(太原科技大学电子信息工程学院, 太原 030024)
齿轮作为机械设备的动力和运动传递部件,由于具有结构紧凑、传动效率高等优点,在工业、航空航天等多领域应用广泛[1-2]。齿轮结构在长期服役过程中经常处于变载荷、变转速等复杂工况下,容易产生齿面磨损、剥落、断齿等故障[3],严重时可能进一步引起整机系统瘫痪,造成巨大的经济损失甚至严重的安全事故。因此,准确检测齿轮运行状态,研究早期齿轮故障诊断方法对保证齿轮设备安全可靠运行具有重要的意义。
故障齿轮由于其表面损伤在啮合时经常伴随碰撞振动现象,使得齿轮局部故障特征耦合在准周期或周期冲击振动中。研究[4-6]表明,齿轮故障振动信号主要表现为以啮合频率及其倍频成分为载波、故障齿轮轴转频及其倍频为调制频率的调幅、调频信号。因此,如何从振动信号中分离出这些特征信号是齿轮故障特征提取的一个关键。然而,早期故障特征信息往往具有微弱性。为了去除噪声干扰,有效提取齿轮故障特征,国内外学者对齿轮故障诊断做了大量研究。针对故障齿轮振动信号的非平稳非线性特点,阙红波等基于扩展卡尔曼滤波和希尔伯特黄变换(Hilbert-Huang translation, HHT)方法辨识故障齿轮啮合频率[7]。为了提高信噪比,邓博元等提出了基于信号经验模态分解(empirical mode decomposition, EMD)与分集合并的齿轮故障诊断方法[8]。然而,EMD模式混淆现象比较严重,为此Dragomiretskiy等[9]提出了变分模式分解(variational mode decomposition, VMD)算法,该方法基于变分优化理论将信号自适应、非递归地分解为一组变分模式函数或分量(variational mode functions, VMFs),这些VMFs围绕其中心频率具有窄带属性。徐甜甜等[10]结合VMD和谱峭度法分解齿轮故障信号,有效滤除低频干扰信号,对降噪信号进行包络解调分析,诊断齿轮故障,分析结果表明所提方法的故障诊断效果优于基于包络解调分析、EMD、集总经验模式分解(ensemble EMD, EEMD)等方法的诊断效果。李玉豪等[11]通过相关系数和峭度指标选择故障冲击分量,提出了基于VMD-相关系数-峭度的方法提取行星齿轮箱故障特征。Wang等[12]通过比较VMD分量中心频率与齿轮啮合频率确定算法模式数参数并选择故障特征分量,提出了基于VMD和信号包络的方法诊断齿轮故障。然而,VMD算法存在参数(如模式数和尺度参数)选择较难、对微弱分量提取效果差、对频率相交的宽带分量分离效果差等问题,为了解决VMD算法存在的不足,学者们提出了一些新算法。Mohan等[13]设计定频分解方案改进VMD算法,利用工频干扰先验信息实现心电图信号降噪。郑近德等[14]借助广义傅里叶正逆变换实现宽带信号与窄带信号的相互转变,提出了一种广义变分模式分解算法并分析故障齿轮振动信号。Chen等[15-16]提出了变分非线性调频模式分解算法和自适应调频模式分解算法,这两种算法均采用解调技术把宽带调频信号转变为窄带信号,在时频域分解信号,对频率接近甚至交叉的调频模式分解效果较好,且能够获得分量的瞬时频率,但它们均不能实现按需分解,且对周期性冲击衰减振动信号的分解效果一般。笔者针对VMD算法对频谱分解位置与频域分解尺度不能根据信号特点灵活控制的不足,改进算法数学模型和求解方案,提出了一种新的广义变分模式分解算法(generalized VMD, GVMD)[17-19],它具有频域多尺度定频分解性能,能够灵活利用故障特征频率与带宽信息实现按需分解。由于齿轮故障特征频率和带宽信息具有一定的先验性,因此,GVMD算法适合分析齿轮故障振动信号。
针对齿轮早期故障特征信息的微弱性和耦合性,现将GVMD算法应用到齿轮故障特征提取中,提出GVMD-峭度-包络谱法实现齿轮故障诊断。首先采用GVMD算法分析故障齿轮振动信号,结合故障特征先验信息与信号特点灵活控制算法频域分解尺度和频谱分解位置,按需分解信号,准确获得包括微弱分量在内的多个感兴趣分量;然后根据峭度准则和齿轮特征频率信息优选冲击特征分量,集成更多故障特征信息重构信号,实现信号降噪;最后通过包络解调技术分析降噪信号,诊断齿轮故障。将所提方法应用于分析煤矿提升机齿轮箱故障振动信号,验证其有效性。
1 理论基础
1.1 GVMD算法
GVMD算法为每个欲得分量单独构建约束优化问题;在优化问题求解方法中加入定频分解方案,从而实现频域多尺度定频分解。GVMD算法的核心是约束优化问题的构建与求解。
1.1.1 变分约束优化问题构造
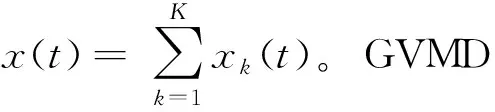
(1)
式(1)中:∂t(·)表示对时间求偏导;δ(·)表示狄拉克函数;uk和ωk为第k个VMF及其中心频率。
与VMD算法模型相比,GVMD算法模型目标函数强调单个子信号的特点,约束函数强调信号的整体重构保真性。因此,GVMD算法能够兼顾信号的局部性与整体性。而VMD为所有分量仅构建一个约束优化问题,难以很好地兼顾信号的局部特点与整体保真度。
1.1.2 变分约束优化问题求解
首先利用乘子方法将约束优化问题(1)转化为无约束优化问题,获得一组增广拉格郎日函数,即
L(uk,ωk,λk)=
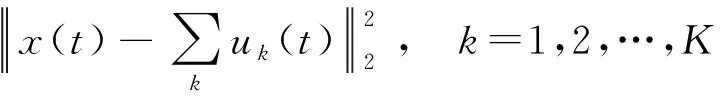
(2)
式(2)中:αk表示尺度参数;λk表示拉格朗日乘子。
由无约束优化问题(2)可见,算法模型为求解每个分量分配独立的尺度参数,为通过改变尺度参数灵活控制算法局部频域分解尺度奠定了理论基础。
为了实现算法定频分解性能,设计定频分解方案改进算法求解流程,从而实现频域多尺度定频分解。GVMD算法具体求解流程如下。
(2)更新循环次数n=n+1。
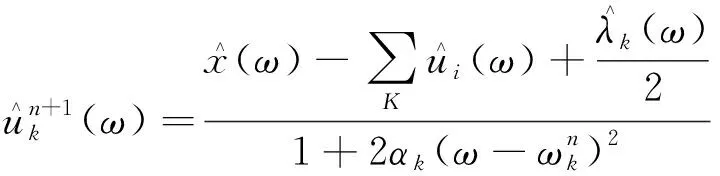
(3)
(4)迭代更新未知的ωk(k=m+1,m+2,…,K):
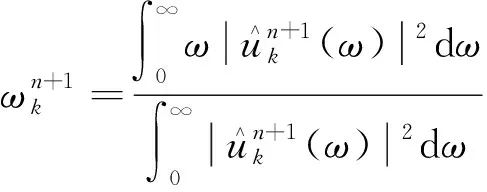
(4)
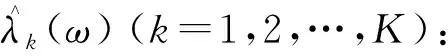
(5)
(6)循环执行第(2)步~第(5)步,直到满足式(6)所示迭代约束条件,则结束迭代。
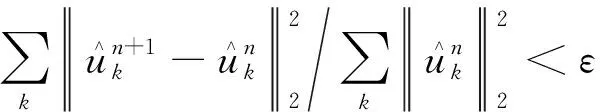
(6)
式(6)中:ε为迭代容许误差。
在齿轮故障特征提取中,可以根据齿轮轴转频、啮合频率等频率信息和信号带宽信息设置GVMD算法模式数、先验中心频率与尺度参数,达到对算法频谱分解位置与频域分解尺度的灵活控制,实现按需分解,准确获得感兴趣的微弱分量。
1.2 峭度准则
峭度是一个描述信号波形尖峰度的无量纲参数,只与信号冲击成分有关,与齿轮尺寸、转速及载荷分布等无关[8,11]。峭度定义为
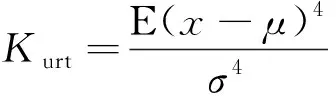
(7)
式(7)中:μ和σ分别表示信号x的均值和标准差;E(·)表示求信号的期望值。
正常齿轮振动信号为平稳信号,其峭度值小于3或接近3,而齿轮故障导致齿轮在啮合过程中伴随碰撞现象,使得其振动信号中含有冲击成分,信号峭度值明显大于3。由此可推断,当某些VMFs的峭度值大于3时,表明这些VMFs含有冲击成分。在实际齿轮故障诊断中,采用峭度准则选择包含冲击特征信息的VMFs,有望获得包含更丰富故障特征信息的重构信号,实现信号降噪。
2 基于GVMD-峭度-包络谱法的齿轮故障诊断方法
针对齿轮故障特征的微弱性和耦合性,将GVMD算法、峭度准则和包络解调技术相结合,提出GVMD-峭度-包络谱法诊断齿轮故障。图1为GVMD-峭度-包络谱法齿轮故障诊断方法的流程图,该方法诊断齿轮故障的具体过程如下。
(1)采用GVMD算法将齿轮振动信号按需分解为若干VMFs,准确获取微弱分量。根据振动信号所含转频、啮合频率及其谐波等的峰值频率信息设置GVMD算法先验中心频率参数;根据欲得分量带宽信息设置尺度参数,为窄带分量定义较大的尺度参数,为宽带分量设置较小的尺度参数。
(2)根据峭度准则和齿轮特征频率先验知识选取故障敏感VMFs。计算分解所得VMFs的峭度值,选择峭度值大于3且特征频率与齿轮啮合频率等接近的VMFs作为故障敏感分量。
(3)重构降噪信号。为了提高信噪比,集成多个故障敏感VMFs重构降噪信号。
(4)对降噪信号进行Hilbert包络解调分析,准确解调故障频率信息,与故障齿轮的特征频率进行比较,实现故障诊断。
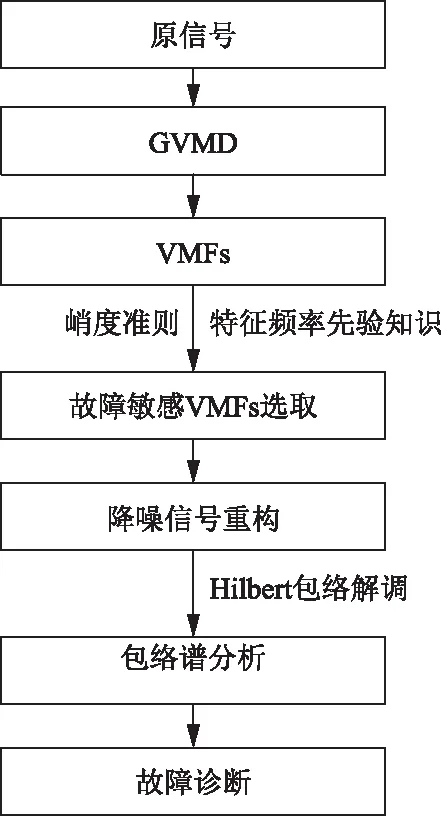
图1 GVMD-峭度-包络谱法齿轮故障诊断流程图Fig.1 Flowchart of gear fault diagnosis based on GVMD-kurtosis-envelope spectrum method
3 GVMD-峭度-包络谱法在齿轮故障诊断中的应用
3.1 分析信号
采用某煤矿提升机齿轮箱上的加速度振动信号验证所提齿轮故障诊断方法的有效性。提升机齿轮传动及传感器安装示意图如图2所示,提升机电机型号为JR158-8,二级减速箱型号为ZHLR-150II,第一级齿数Z1=19,Z2=75,第二级齿数Z3=30,Z4=152;电机转速为735 r/min。经计算可得输入轴、中间轴及输出轴的转频分别为12.25、3.10、0.61 Hz,第一、二级齿轮啮合频率分别为232.75 Hz和93.10 Hz。
图3为振动烈度超过允许值时所测的减速箱加速度振动信号,采样频率fs为8 kHz,数据时长为5 s。由图3可见,信号波形中存在明显的冲击现象,信号能量主要集中在0~1 500 Hz频段。结合信号频谱分布与齿轮啮合频率信息,在0~1 500 Hz频段发现存在第2级齿轮啮合频率93.7 Hz及其二倍频187.5 Hz,以及第一级齿轮啮合频率234.3 Hz及其2~6倍频468.8、703.2、936、1 172、1 405 Hz等多个特征频率。除468.8 Hz邻域频带信号外,其余特征频带信号相对微弱。
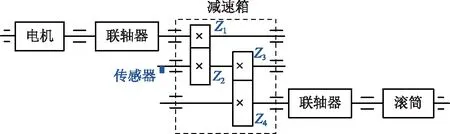
图2 提升机齿轮传动及传感器安装示意图Fig.2 The Schematic diagram of elevator gearbox transmission and sensor installation

图3 原信号Fig.3 The original signal
3.2 基于GVMD-峭度-包络谱法的齿轮故障诊断
首先,采用GVMD算法分解图3所示信号,根据齿轮啮合频率、带宽信息(根据啮合频率周围边频带分布定性确定欲得分量带宽相对大小)以及信号特点设置GVMD算法参数为:先验中心频率f=[93.7,187.5,234.3,468.8,604.5,703.2,936,1172,1405,0]/fs、模式数K=10、先验中心频率数m=9和尺度参数α=[5 000,8 000,5 000,3 000,3 000,3 000,1 500,1 500,1 500,100]。GVMD分解结果如图4所示,VMF1和VMF2分别估计第一级啮合频率及其2倍频成分,VMF3、VMF4、VMF6~VMF9分别估计第二级啮合频率及其2~6倍频成分;VMF5为604.5 Hz邻域频带的干扰分量,VMF10为剩余信号的近似。可见,由于GVMD算法具有频域多尺度定频分解属性,根据齿轮啮合频率先验信息与信号频谱分布特点设置其主要参数,它能够按需提取多个微弱分量,为提取齿轮早期故障微弱特征奠定基础。
其次,根据峭度准则和齿轮特征频率先验信息选取故障敏感VMFs。所得VMFs的峭度值如表1所示,其中主分量VMF4和微弱分量VMF6、VMF7及VMF9的峭度值大于3,认为它们包含故障冲击信息,对故障敏感;而且这4个特征分量均为齿轮第1级啮合频率(约234.3 Hz)的倍频成分,说明齿轮冲击振动来自齿轮Z1和Z2啮合振动。
第三,重构降噪信号。由主分量VMF4和微弱分量VMF6、VMF7及VMF9重构降噪信号,其峭度值(即4.783 1)比任何单个分量的峭度值大,说明降噪信号包含了更多的齿轮故障特征信息;降噪信号的峭度值也比原信号的峭度值(即4.173 7)大,说明降噪信号更能突出故障冲击信息。
最后,对降噪信号进行解调分析,诊断齿轮故障位置。降噪信号的包络谱图如图5所示,3.1 Hz频率成分(即1×)及其倍频幅值较大,表明信号调制源来自中间轴,因此,进一步推断故障发生在中间轴齿轮Z2中。
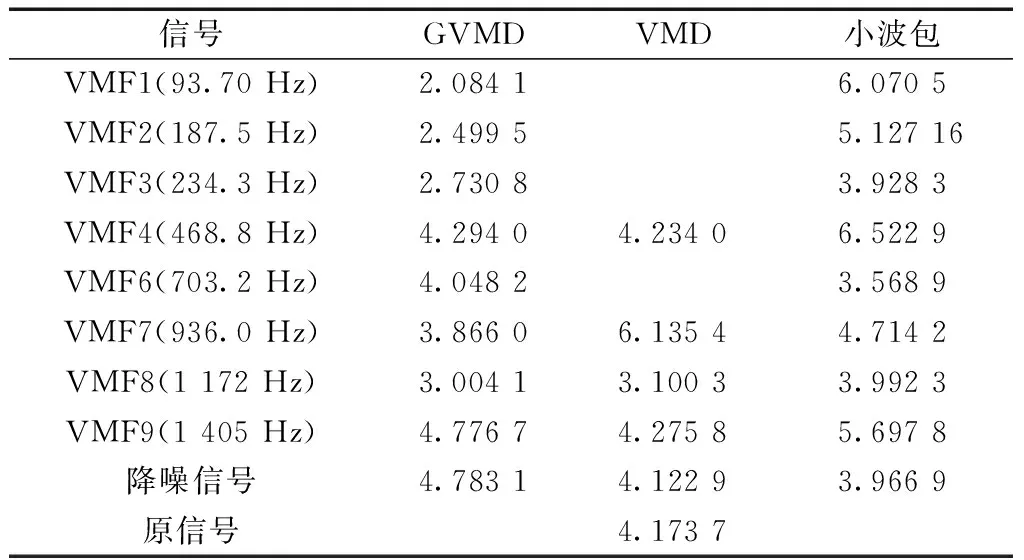
表1 分量峭度值Table 1 Kurtosis values of the components
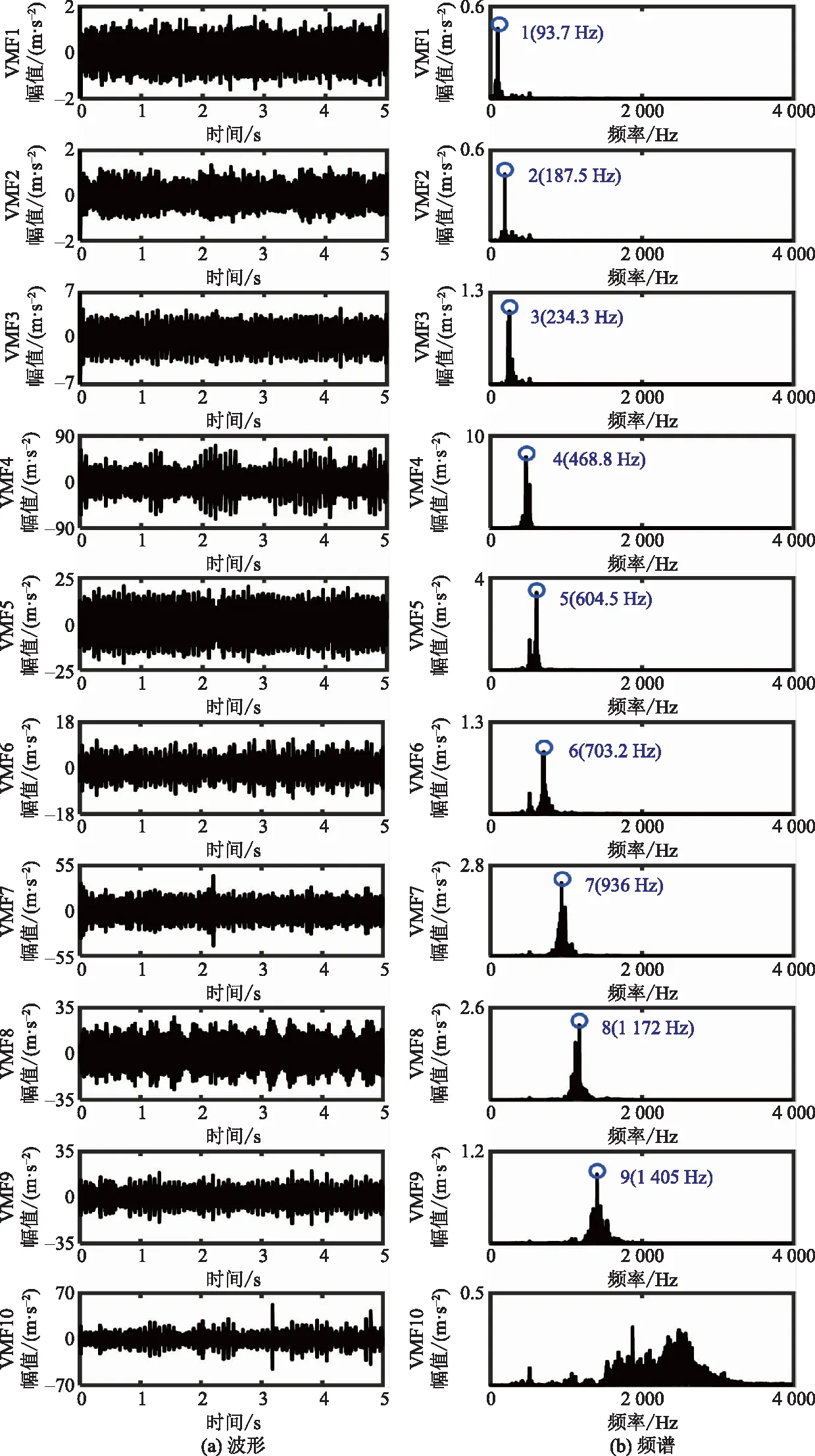
图4 GVMD分解结果Fig.4 The results of GVMD
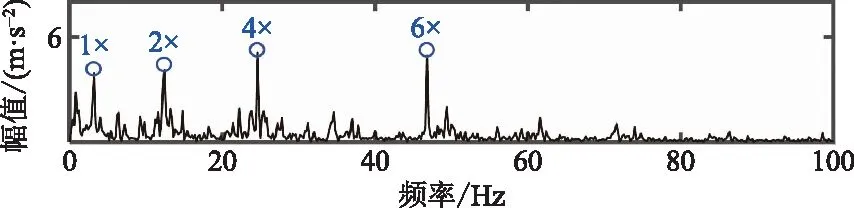
图5 GVMD故障齿轮降噪信号包络谱Fig.5 The de-noised signal envelope spectrum of GVMD for the fault gear
3.3 降噪方法比较
为了突出GVMD算法在信号降噪方面的优越性,分别采用基于VMD和小波包(wavelet packet transform,WPT)的方法对图3所示信号进行降噪。
图6(a)为VMD分解所得结果的幅值谱,其中VMD算法模式数为10,尺度参数为1 000。图中VMF1、VMF3、VMF7和VMF8分别近似第二级啮合频率的2倍频、4倍频、5倍频和6倍频分量,其他VMFs均为干扰成分。可见,由于VMD算法不具有定频分解性能,导致它未能将微弱的第一级啮合频率及其二倍频分量以及第二级啮合频率的3倍频分量从原信号中分离出来;由于VMD算法不能根据信号带宽特点为其设置不同的尺度参数,灵活控制算法局部频域分解尺度,导致所得分量容易受到邻域频率分量的干扰,如图6中VMF1和VMF3受到低频分量干扰(如图中蓝色虚线框所示)。
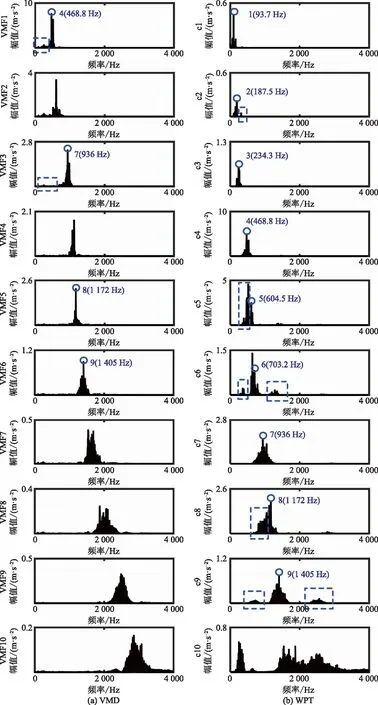
图6 VMD和WPT分解结果的幅值谱Fig.6 The amplitude spectrums of the results of VMD and WPT
图6(b)为WPT所得结果的幅值谱,其中母小波选“Daubechies9”小波函数,分解层数设为6层,根据齿轮故障频率信息及小波包频带划分规则,通过选频重构方法获得8个感兴趣分量的近似。c1和c2分别估计第一级啮合频率及其2倍成分,c3、c4、c6~c9分别估计第二级啮合频率及其2~6倍频成分;c5为频率为604.5 Hz的干扰分量,c10为其余频段信号的近似。可见,小波包能够较好地获得全部感兴趣的微弱分量,但WPT存在能量泄漏问题(如图中蓝色虚线框标注部分),容易造成微弱特征信息混淆或损失。
同样,根据峭度准则与齿轮啮合频率先验信息选择故障敏感分量重构降噪信号。由表1可知,VMD和WPT降噪信号峭度值分别为4.122 9和3.966 9,均低于GVMD算法降噪信号的峭度值。因此,认为本文所提方法所得降噪信号包含更丰富的故障特征信息,有望获得更可靠的诊断结果。
4 结论
针对齿轮早期故障特征的微弱性和耦合性,提出了GVMD-峭度-包络谱法诊断齿轮故障。通过本文的研究可以得出以下结论。
(1)根据齿轮故障特征信息和信号特点灵活设置模式数、先验中心频率参数及尺度参数,GVMD算法能够按需分解信号,准确获取微弱分量,有效克服了VMD和WPT对微弱特征信息提取存在的问题,为提取齿轮早期故障微弱特征信息奠定基础。
(2)实验分析表明,所提方法能够获得更多微弱故障信息诊断齿轮早期故障,准确识别齿轮故障位置。

