基于应变能理论的端齿弯曲刚度及其转子动力学特性影响研究
邱欣可,曾 武,高 庆,满吉鑫
(1.中国科学院工程热物理研究所先进燃气轮机实验室,北京 100190;2.中国科学院先进能源动力重点实验室(工程热物理研究所),北京 100190;3.中国科学院轻型动力创新研究院,北京 100190;4.中国科学院大学,北京 100049)
重型燃气轮机多采用拉杆式转子结构,即采用一根位于轮盘中心或多根位于轮盘周向的拉杆[1-3],各级轮盘之间采用端齿定心传扭,并在轴向预紧力的作用下将各级轮盘串联拉紧。根据端齿的结构不同,可以分为Hirth齿与圆弧端齿[4-5],Hirth齿的齿面为平面,圆弧端齿的齿面为曲面。由于在端齿连接处存在大量的接触面,由此带来的结构不连续性会导致不可忽略的弯曲刚度损失,进而影响转子系统的动力学特性。因此,端齿弯曲刚度损失问题的研究对转子的安全可靠运行有着十分重要的意义。
端齿的刚度损失问题很早就被学者所关注,早期的研究以理论分析计算为主,即通过对端齿模型进行简化,得出端齿的连接刚度特性。上世纪90年代,尹泽勇等[6]提出了端齿梁元模型,即在不考虑摩擦的条件下,端齿与梁单元的刚度矩阵具有相同的形式,并通过端齿梁元模型对某端齿连接转子的固有频率进行了计算,结果与实测值符合较好。随后,在文献[7]中研究了端齿轴段弯曲刚度及轴向预紧力的变化对转子的刚度与固有频率的影响。
随着计算机技术的发展,有限元计算研究方法已经成为研究转子动力学问题的主要手段。Pisani等[8]对比了边界元与有限元方法的计算结果,二者结果相似。而有限元方法相较于边界元方法在网格划分等方面具有更好的可操作性,因此后续研究通常采用有限元方法进行计算研究。Richardson等[9]通过三维有限元方法计算得出了端齿的力学特性,并通过光弹试验验证了计算结果的正确性。
通过三维有限元计算,文献[10-11]研究了端齿弯曲刚度随预紧力与弯矩的变化关系,得出了端齿弯曲刚度受到预紧力与弯矩产生的轴向脱开力的相对大小关系的直接影响的结论。在此基础上分析了弯曲刚度损失对转子系统固有频率的影响。高进等[12]通过实验分析了预紧力对端齿弯曲刚度特性的影响,实验结果与有限元计算结果吻合较好。葛庆等[13]针对齿数对端齿弯曲刚度的影响进行了研究。
随着研究的深入,通常需要面对多载荷强耦合的工况,端齿的变形通常难以准确计算,而应变能理论则可以精确地计算出相应的刚度。因此,应变能理论逐渐被学者所关注。李浦等[14]证实了应变能理论在刚度计算上的可行性,并对某转子的轴向与扭转刚度进行了计算研究。
端齿刚度对转子系统的影响也是一大研究热点。对于端齿连接的转子结构,现有的计算条件无法对带有真实端齿模型的转子系统进行计算,尤其是对于多级端齿的转子,计算成本更高,因此目前主要采用文献[15-16]提出的薄层单元理论,建立端齿的等效弹性模量或等效刚度直径模型,以分析端齿连接转子的刚度与模态特性。杨郑烈等[17]通过建立等轴向刚度的薄层单元研究了不同预紧力对端齿连接转子模态特性的影响。然而对于多级端齿连接的转子系统,不同级端齿的影响也各不相同,目前尚未有文献针对不同级端齿对转子系统动力学特性的影响展开研究。
综上,目前对于端齿弯曲刚度的相关研究已经具有一定的基础,但基于应变能理论的弯曲刚度计算应用较少,端齿的弯曲刚度损失对转子系统的影响研究还不够完善,尤其是对于多级端齿连接的转子动力学特性研究较为缺乏。基于上述研究现状,本文通过应变能理论对某H级重型燃气轮机转子端齿刚度及转子动力学特性进行了研究。
1 端齿的结构与参数化建模
如图1所示,该型燃气轮机各级压气机盘、涡轮盘和前后转接盘之间以端齿连接,共有24级端齿,端齿种类为Hirth齿。其中部分级端齿结构参数不同,故首先对端齿进行参数化建模,以方便获得具有不同结构参数的端齿模型并建立相应的转子模型。
根据端齿的结构特点,其齿面为三角形。图2为端齿不同方向视图。
图2中,α为齿顶角,R为齿底倒圆半径,H为三角形高,L1为齿高,L2为齿根高,c为齿顶间隙,a1与a2分别为端齿内径与外径处齿宽,W为齿顶斜角,R1、R2分别为端齿内半径与外半径。图2(a)中虚线为端齿节线,图2(c)中虚线为端齿轴线,齿数Z未在图中标出。

(a) 带有端齿的转子模型

(a) 齿面图
根据端齿结构参数间的相互关系,部分参数之间可以相互确定,如:
(1)
(2)
(3)
c=R
(4)
通过端齿结构参数间的几何关系,编写基于UG的宏文件,实现了端齿的参数化建模,即可以任意地输入端齿关键参数并快速得到相应的端齿几何模型。图3是齿数为120、齿顶角为60 °、齿底倒圆半径为5 mm的端齿几何模型。

图3 端齿三维几何模型
2 端齿弯曲刚度研究
2.1 应变能理论
由于端齿的复杂结构,在端齿发生弯曲变形时,无法得到其弯曲刚度的理论解,而应变能与刚度的关系较为简单,且应变能是一个标量,不同载荷所产生的应变能可以简单相加,因此在复杂结构或受到多载荷的情况下能够有效地简化计算。
当物体在受到压缩、弯曲、扭转等载荷作用时,物体会发生形变,从而产生应变能。而由于不同物体的刚度不同,因此产生的应变不同,从而导致应变能的大小也不同。根据应变能的定义,应变能U为应力σ在应变微元dε下的体积分:
U=∭σdε
(5)
对于端齿结构,其截面为圆环,若忽略端齿的不连续面将其视为刚性一体化连接模型,则可以得出该圆环模型受到轴向预紧力与弯矩载荷时的应变能。根据式(5),在线弹性范围内,当模型受到轴向力时,应变能U1可以写为:
(6)
式中:F为圆环模型受到的轴向力;L为圆环模型的轴向长度;E为材料的弹性模量;A为圆环模型侧面圆环的面积。
当模型受到弯矩载荷作用时,应变能U2可以写为:
(7)
式中:M为圆环模型受到的弯矩载荷;Id为绕某一直径的惯性矩;L、E与式(6)中相同。
由式(7)可以看出,弯矩产生的应变能与其弯曲刚度成反比,即应变能越大,弯曲刚度越小。若考虑实际端齿模型,当其受到轴向预紧力与弯矩同时作用时,可采用三维有限元计算的方法求得应变能。若端齿模型在轴向预紧力与弯矩作用下产生的总应变能为Ut,预紧力所产生的应变能为Upre,弯矩产生的应变能为UM,则有:
Ut=Upre+UM
(8)
根据应变能与刚度的关系,结合有限元计算所得出的端齿应变能,即可得出对应的弯曲刚度。对于刚性一体化模型,若其弯曲刚度为K0,当受到弯矩载荷时,其应变能U0可以通过式(7)直接计算得出。对于实际端齿,则可通过有限元计算结果与式(8)得出由弯矩产生的应变能UM。由此,可以通过刚性一体化模型和端齿实际模型的应变能之比来定义弯曲刚度系数β:
(9)
式中:K为端齿实际弯曲刚度。
通过弯曲刚度系数β来表征实际状态下弯曲刚度的损失情况。
端齿在受到轴向预紧力与弯矩载荷作用时,轴向预紧力Fa在端齿端面产生的名义压应力:
(10)
式中:Ac为端齿侧面面积。
(11)
端齿受到弯矩载荷M而产生的轴向脱开应力:
(12)
式中:R2为端齿的外半径;Id为端齿绕某一直径的惯性矩。
定义无量纲载荷因子γ:
(13)
式中:σ为弯矩产生的轴向脱开应力;P为轴向预紧力产生的名义压应力。
显然,端齿接触面状态受到无量纲载荷因子γ的影响,因此将针对γ与弯曲刚度的关系展开研究分析。
2.2 有限元计算分析
基于上述应变能理论分析,可以计算出端齿变形时的应变能,进而得出端齿的弯曲刚度特性。
选取某一级端齿为研究对象,材料弹性模量E=208 GPa,外直径D2=1 556 mm,内直径D1=1 416 mm。对端齿采用扫掠划分的方法进行网格划分,单元类型为20节点六面体单元solid186。端齿啮合面采用frictional接触方式。有限元网格模型如图4(a)所示,载荷边界条件如图4(b)所示。端齿两侧端面采用多点约束MPC方式与中心节点绑定在一起,并在其中一侧中心节点上分载荷施加轴向预紧力Fa(图4(b)中A位置)与弯矩载荷M(图4(b)中B位置),固定弯矩大小M=1×106N·m,另一侧施加固定约束(图4(b)中C位置)。在不同预紧力条件下计算端齿在对应载荷条件下弯矩产生的应变能UM。同时,通过式(7)求得刚性一体化整体轴段模型在相同弯矩下所产生的应变能U0。根据式(9),将U0与UM相比,得出端齿的弯曲刚度系数β,并进一步得出端齿的实际弯曲刚度值,为后续转子系统动力学计算做好铺垫。

图4 端齿有限元模型
2.3 计算结果分析
根据2.1节所述应变能理论分析与2.2节所建立的端齿有限元模型,得出相应的应变能与弯曲刚度系数。计算结果如表1与图5所示。

表1 不同无量纲载荷因子γ下弯矩产生的应变能

图5 端齿弯曲刚度系数随量纲载荷因子γ变化曲线
由表1,当无量纲载荷因子γ<1时,端齿由弯矩所产生的应变能几乎不发生变化;而当γ>1时,应变能迅速增大,即如图5所示的变化曲线。计算结果与文献[10-12]中所反映出的规律十分吻合,均呈现出当预紧力大于弯矩产生的轴向脱开力时(完全预紧时,γ<1),弯曲刚度基本保持稳定;而当预紧力小于弯矩产生的脱开力时(γ>1),弯曲刚度迅速下降。
通过上述计算,可以反映出应变能理论在弯曲刚度的计算上有着方便简洁的优点。对于多载荷的情况,可以利用应变能的标量性来简化计算与分析。而对于复杂的非连续结构也可以通过应变能来体现其弯曲刚度损失情况,具有一定的工程应用价值。
3 端齿弯曲刚度损失对转子系统动力学特性的影响
3.1 端齿简化模型
以研究的燃气轮机转子为例,该转子共有24级端齿,且结构复杂,现有的条件已无法计算,故需要对端齿进行简化。
根据文献[15-16]提出的薄层单元理论,可以将端齿简化为圆环结构(如图6所示),简化过程遵循等质量、等弯曲刚度的原则。圆环结构的内外径、密度、轴段长度均与实际端齿相同,以保证等质量原则;通过调节圆环的弹性模量以保证等弯曲刚度原则。需要说明的是,在不考虑陀螺力矩与阻尼的前提下,转子的刚度与模态特性完全由系统的刚度矩阵与质量矩阵决定,因此此种简化方式可以保证刚度与模态特性的可靠性。

图6 端齿简化模型
为了保证端齿简化模型与实际端齿模型具有相同的弯曲刚度,在密度、内外径与轴段长度均与实际端齿模型相等的情况下,圆环结构的等效弹性模量可以由式(14)得出:
(14)
式中:Eeq为等效弹性模量;K为端齿实际弯曲刚度。
根据转子端齿齿形参数,齿数Z=120,齿顶角α=60 °,齿底倒圆半径R=5 mm。结合第2章计算分析,得出端齿在完全预紧状态下的弯曲刚度,进而求得端齿简化模型的等效弹性模量Eeq。各级端齿结构参数与对应的简化模型的等效弹性模量如表2所示。

表2 不同级端齿的结构参数与对应的等效弹性模量
3.2 端齿刚度损失对转子临界转速的影响
借助3.1所建立的端齿简化模型,对端齿连接转子的模态特性进行研究。
对于如图7所示的多盘转子系统而言,根据转子动力学原理[19],当转子转速为Ω时,将轮盘盘心O′向xoz与yoz平面投影,并建立坐标系。第j个圆盘惯性力主向量Rj与惯性力主矩向量Lj在ox与oy轴上的分量为Rjx、Rjy、Ljx与Ljy:

图7 轮盘-转子结构理论模型
(15)
式中:e为偏心距;Φ为偏心角;Jd为绕直径的转动惯量;Jp为绕圆心的转动惯量;m为轮盘的质量;u与θ分别为线位移与角位移。下标变量中:j表示第j个轮盘的参数;x、y分别表示该物理量在x或y方向的分量。变量的一阶与二阶导数均指的是对时间的导数。
根据D’Alembert原理,x、y方向的线位移uxi、uyi与角位移θxi、θyi为:
(16)

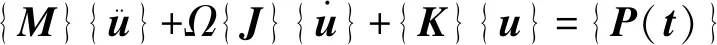
(17)
式中:{M}为转子系统质量矩阵;{J}为转动惯量矩阵;{K}为刚度矩阵;{u}为位移矩阵;{P(t)}为离心力载荷矩阵。
当转子转速不同时,式(17)的解也不同,而当转子处于某一特定转速Ω时,转子振动变形处于极大值,故此时对应的转速Ω为转子的临界转速。根据式(17)解的性质,最大振幅对应的转速只与刚度、质量与阻尼特性有关,而与外载荷{P(t)}无关。因此在求解转子临界转速时不需要施加不平衡载荷,且在不考虑质量与阻尼变化的前提下,不同端齿结构参数与预紧工况的改变对端齿弯曲刚度的影响也完全能通过等效模型的弹性模量体现。
根据转子的约束行为,建立转子系统的有限元模型。转子采用1-0-1支承方案,前轴颈处采用可倾瓦推力轴承约束轴向、周向和径向自由度,后轴颈处约束径向和周向自由度。各级端齿简化模型与轮盘采用绑定约束。定义弯曲刚度损失系数λ:
λ=1-β
(18)
通过调节端齿等效模型的弹性模量可模拟端齿的不同弯曲刚度损失系数。图8为转子系统的有限元网格模型。在此基础上计算转子的前两阶弯曲临界转速与振型(其他阶次模态受弯曲刚度影响较小,故已省去),临界转速计算结果如表3所示,振型云图如图9所示。

图8 转子有限元网格模型

(a) 一阶弯曲模态振型
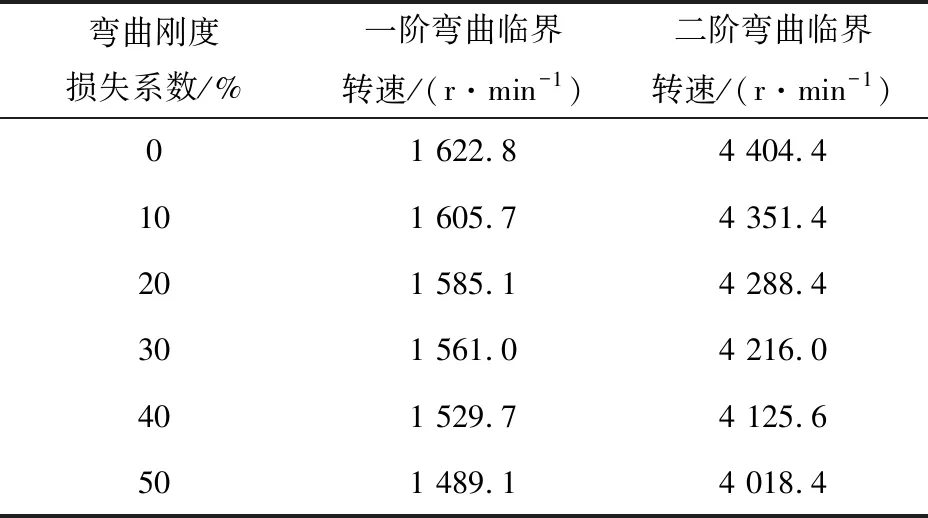
表3 端齿不同弯曲刚度损失系数下转子的临界转速
表3给出了端齿在不同弯曲刚度损失系数下转子系统的一、二阶弯曲临界转速,振型如图9所示。当弯曲刚度损失达到50%时,一阶弯曲临界转速降低了8.2%,二阶弯曲临界转速下降了8.8%,且表现为随着端齿弯曲刚度损失系数增大,前两阶弯曲临界转速呈加速下降趋势。而端齿的弯曲刚度损失对转子的振型几乎没有影响。需要注意的是,该燃气轮机工作转速为3 000 r/min,二阶弯曲临界转速已经远超过其工作转速,故后续仅分析一阶弯曲临界转速。
3.3 不同级端齿刚度损失对转子系统刚度与模态特性的影响
对于多级端齿连接的拉杆转子系统,每一级端齿的位置、尺寸大小不同,对转子动力学特性的影响也不相同,故需要针对不同级端齿对转子系统动力学特性的影响展开研究。
首先采用简支梁模型进行理论推导,定性地确定不同级端齿对转子刚度特性影响分布,在此基础上通过有限元计算分析转子模态特性的变化。采用图10所示的简支梁来近似模拟转子,前支点为固定约束,后支点为径向、周向约束,均布载荷F0=ql0代表转子所受的重力。

图10 转子对应的简支梁模型
图中,q为载荷集度,l0为梁的轴向长度,Mr为固定约束处的支反弯矩,F1、F2分别为前、后支点处支反力。根据材料力学理论可推导出梁在支座处的支反力,进而得出梁的弯矩方程M(d)为:
(19)
式中:d为所研究的点距离梁左端点(前支点)的距离。
梁上任意一小微元的应变能u(d)为:
(20)
式中:E为弹性模量;I为截面惯性矩。
将式(19)代入式(20),得到不同位置处的应变能分布函数:
(21)
显然,当梁的约束行为不同时,支反力、弯矩方程均会不同,从而引起应变能函数不同,进而对该分析的结果产生影响。
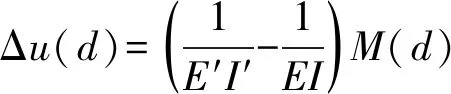
在上述理论分析的基础上,进行对应的有限元计算分析。图11给出了转子系统在重力载荷作用下各级端齿的应变能情况。

图11 不同级端齿在重力作用下的弯曲应变能
由图11中可以看出,在重力载荷作用下,1级端齿的应变能最大,4级端齿应变能最小,14级端齿处应变能取得了极大值。有限元计算结果与上述理论分析较为吻合。因此,着重研究1级、4级和14级端齿对转子系统刚度与动力学特性的影响。分别计算了当1级、4级、14级端齿的弯曲刚度系数β达到0.5而其他级端齿不发生弯曲刚度损失时转子系统的刚度与模态特性变化。计算结果如表4、表5所示。

表4 不同级端齿弯曲刚度损失时转子弯曲刚度
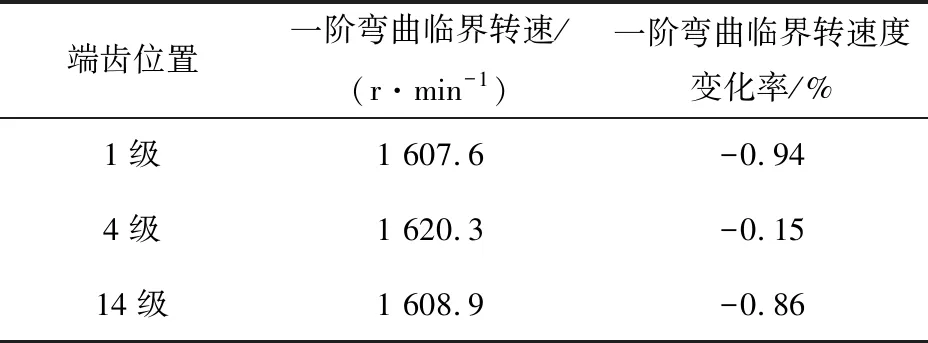
表5 不同级端齿弯曲刚度损失时转子一阶弯曲临界转速
由表4可以看出,当仅有某一级端齿的弯曲刚度降为整体轴段刚度的50%时,1级端齿对转子系统的刚度影响最大,而4级端齿影响最小。对比表5与表3中刚性一体化转子临界转速结果可以看出,1级端齿弯曲刚度发生损失时,临界转速降低幅度最大,14级端齿次之,4级端齿变化幅度最小。计算结果与上述理论分析结果吻合较好,即1级端齿的弯曲应变能较大,弯曲刚度较小,且当其弯曲刚度发生变化时,其应变能变化量相较于其他级端齿更大,对转子系统刚度的影响也越大。4级端齿则相反。转子系统在1级端齿处,由于靠近轴承约束处,该处的弯曲变形相对较大,因此弯曲刚度较小,而在14级端齿处,由于靠近转子中部,因弯曲产生的横向挠度较大,也会使得弯曲刚度较低。因此,对于该转子系统,应着重注意1级与14级端齿的接触与刚度情况,保证良好的接触与足够的弯曲刚度。
4 结论
本文针对某型号燃气轮机转子端齿结构的弯曲刚度展开研究,得出以下结论:
(1) 通过应变能理论计算所得到的弯曲刚度结果与文献[10-11]中研究结果所反映出的规律吻合较好。在完全预紧状态,应变能保持稳定。而当预紧力不足以抵抗弯矩产生的轴向脱开力时,应变能急剧上升。应变能越大表明刚度越低,可以直观地反映端齿的弯曲刚度水平。在实际工程中对于多载荷条件与复杂结构的弯曲刚度计算上能够起到一定的简化作用。
(2) 通过建立端齿等效模型,研究了端齿不同弯曲刚度损失比例对转子系统模态特性的影响,即随着刚度损失增大,转子的弯曲模态对应的临界转速呈加速下降趋势。对于该转子而言,端齿弯曲刚度修正比例达到50%时,相较于刚性一体化转子中其一阶临界转速会下降8.2%。
(3) 通过简支梁模型与应变能理论定性地分析了转子不同级端齿对转子系统刚度与模态特性的影响,并通过三维有限元计算方法得出了与理论分析相吻合的结论。对于所研究转子,1级端齿对转子系统动力学特性影响最大,4级端齿影响最小。因此在工程设计中应对相应级端齿进行特别处理以提高其弯曲刚度。且端齿弯曲刚度损失对转子模态特性的影响主要体现在一阶弯曲模态上,一阶临界转速的降低比例也更大。后续研究应当着重关注在一阶临界转速处转子的不平衡响应情况。
(4) 对于不同约束或支承方案的转子系统,由于支承不同,约束处支反力也不同,因此导致应变能函数不同,进而使得不同级端齿对转子系统的动力学特性影响也不同。

