基于梯度提升决策树的气体传感阵列识别方法

张志业，葛志强，赵小娟，林永江

（国能（泉州）热电有限公司，福建泉州 362804）

气体传感器具有交叉敏感性，容易受温度、湿度、环境条件等因素影响，且稳定性和选择性较差，仅限于精度较低、分辨率低、气体组分简单的应用中[1]。在复杂气体或气味的定性和定量检测中应用较少。受气体传感阵列识别环境影响，仅使用单种传感器无法对某种气体进行精准识别[2]。为此，采用多种传感器进行气体传感阵列的识别成为重要方式。通过气体识别技术能够实现气体成分检测，这是当前气体识别技术改进的主要方向[3]。目前，使用主元统计方法识别气体传感阵列，能够在最小均方计算模式下分析气体数据，虽然该方法能够自动分离不同气体，但该方法受气体主成分影响，缺乏自主学习能力，无法完成数据预处理，导致气体识别结果不精准；使用基于人工神经网络理论识别时，利用MATLAB 软件对所采集的气体实验数据进行识别与分析。该方法虽然识别速度较快，但缺少对冗余数据处理步骤，导致气体识别结果不精准。

为此，该文提出基于梯度提升决策树的气体传感阵列识别方法。

1 气体传感阵列识别方法设计

1.1 混合气体组成成分分析

利用某公司生产的RCS2000-A 型号气体分配系统，获取需要识别的混合气体[4]。该设备采用世界上最先进的气体配气技术，可输出高质量、高精度的混合标准气体，并由计算机自动分配[5]。多组分混合气体从配气方案制定到实施，通过计算机监控，实现了多组分混合气体的自动分配过程，该方法自动化程度高，能够分类处理多种气体数据，具有稳定性较强的优势[6-8]。

通过配置多组混合气体，将高纯度N2作为研究对象，配制多组分混合气时，原料气G1～G6为高纯度稀释气体，原料气浓度为s1～s6。配制不同浓度混合气体时，稀释比为：

在式（1）所示的组分气体稀释比下，对比分析原料气G1～G6的流量fG1～fG6和高纯度N2稀释后流量fN2的比值，计算结果为：

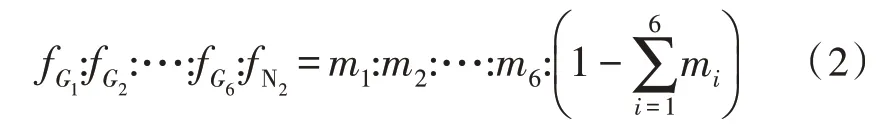
依据式（2）计算结果可知，气体流量控制器采用流量比控制各组分原料气、稀化气流量，可准确、动态地分析多种组分混合气[9]。

1.2 样本数据归一化处理

以变压器油为例，通过对气体传感阵列数据的分析，确定变压器工作状态[10]。变压器工作产生CO 时，说明该设备工作不灵敏，但仍能继续工作；当出现H2时，说明该设备工作时产生的摩擦热较高，此时气体浓度高于150 ppm，需要考虑变压器是否被烧坏；当出现C2H2时，应严格检查变压器能否正常工作，一旦浓度超过5 ppm时，应考虑该设备是否已经损坏[11-12]。

利用SVM 直接分析传感器阵列测得的变压器油色谱数据中气体浓度，可直接获得潜在有价值的微小量信息[13]。因此，对气体传感阵列数据进行归一化处理，采取这种处理方法是为了尽可能完整地保留数据信息，使数据差异降到最低[14]。

经过归纳分析，发现气体样本的标准化范围介于[0,1]和[-1,1]之间，[0,1]之间的数据按统计概率依次分布，[-1,1]之间的数据按坐标分布依次分布[15]。模型建立与计算的基本度量单位相同，该文使用梯度提升决策树，通过训练步骤和预测步骤，获取统计样本坐标。根据scale 函数对传感阵列识别数据进行归一化处理，其公式为：

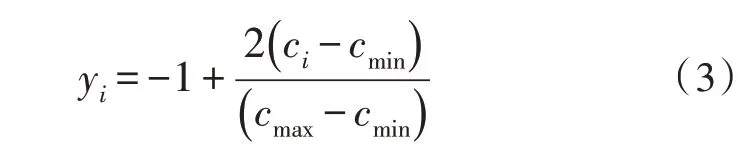
式（3）中，yi表示归一化数据，ci表示传感阵列数据，cmax、cmin分别表示传感阵列数据最大值与最小值。

经过scale 函数对识别数据进行归一化处理后，获取存储气体传感阵列数据，并将阵列进行数字编号[16]。

在获取的数据集中，经归一化的气体数据均在[-1,1]的范围内，有效地减小了不同数据间的差异，从而提高归一化模型的收敛性。在使用测试样本检验现有模型时，数据的标准化是为了保证数据的一致性。

1.3 基于梯度提升决策树的识别方案设计

将梯度提升决策树识别方式看成是数据处理、分类与回归的过程，梯度提升决策树是由若干决策树组成，采用加法模型和正态分布算法对模型进行修正，并逐步逼近最佳解，可以有效地降低各因素间的冗余，对离群点具有较好的鲁棒性[17-19]。该方法能够消除异常点，弥补传感器脆弱性引起的信号异常缺陷，提高气体最终识别的准确性。

假设气体传感阵列P中包含R个传感阵列，每个传感阵列中有xj个识别项目，其中，xi为第i个传感阵列的识别项目。输入向量可表示为：

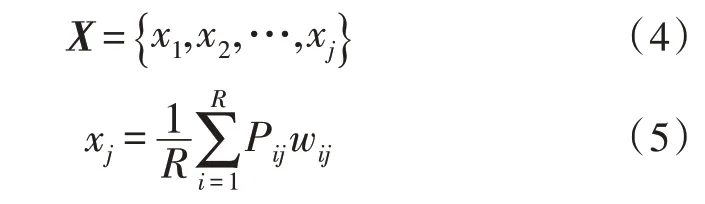
式（4）、（5）中，X表示输入向量；wij表示第i个传感阵列的第j个识别项目权重，其计算公式为：

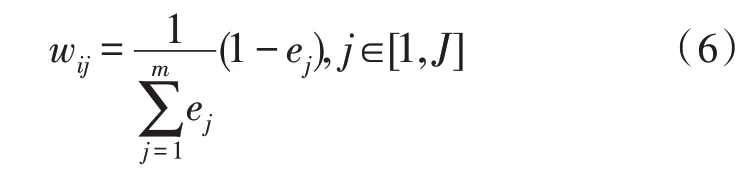
式（6）中，ej表示第j个识别项目的输出熵。

采用梯度提升决策树融合多个决策树模型，通过比较迭代损失函数梯度，构建高精度识别模型。其中，损失函数表达式为：

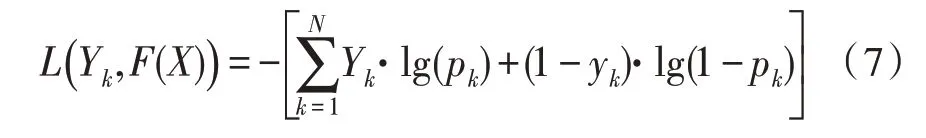
式（7）中，pk表示预测概率；F(X)表示比较迭代损失函数的梯度。

此时，第t轮第i个样本对应种类的负梯度误差，计算公式为：

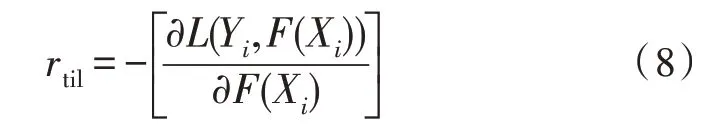
累加梯度提升决策树，对负梯度误差进行修复，并逐步趋近最优解。

基于此，结合SVM-predict 识别程序识别出六组气体，如表1 所示。

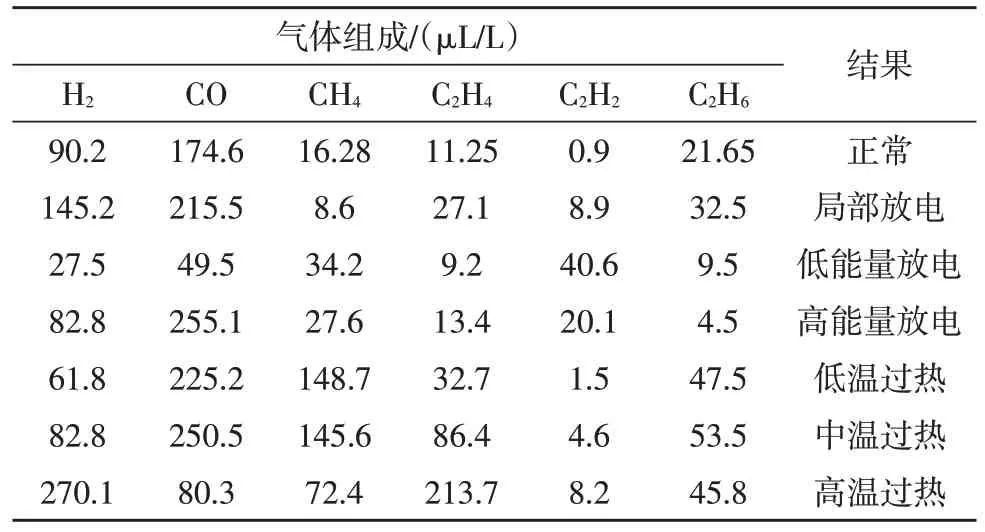
表1 气体传感阵列识别结果

2 实例分析

为了检验基于梯度提升决策树的气体传感阵列识别方法的合理性，选择七组实验样本进行测试。这七组实验样本分别模拟变压器工作时出现故障时不同组分气体含量，如上述表1 所示。

2.1 气体监测实验装置

利用六种不同材料的碳纳米管气敏传感器，将H2、CO、CH4、C2H4、C2H2和C2H6进行分类处理。实验传感装置使用碳纳米金叉指电极结构，以此识别气体传感阵列。实验测试装置结构如图1 所示。

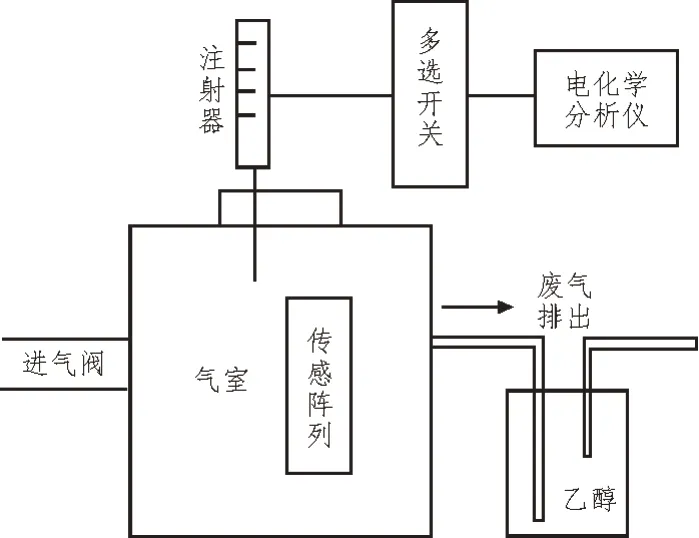
图1 气体监测实验装置

由图1 可知，通过电化学分析仪在恒温情况下分析流入气体。

2.2 结果与分析

为了验证该方法比主元统计方法、基于人工神经网络理论的模式识别方法更优，分别采用三种方法进行气体识别，其经过传感阵列后获取气体浓度值，分别采用主元统计方法、基于人工神经网络理论的模式方法和基于梯度提升决策树的方法进行识别，将识别结果与实际值比较分析，表1 数据为实际值，识别结果如图2 所示。

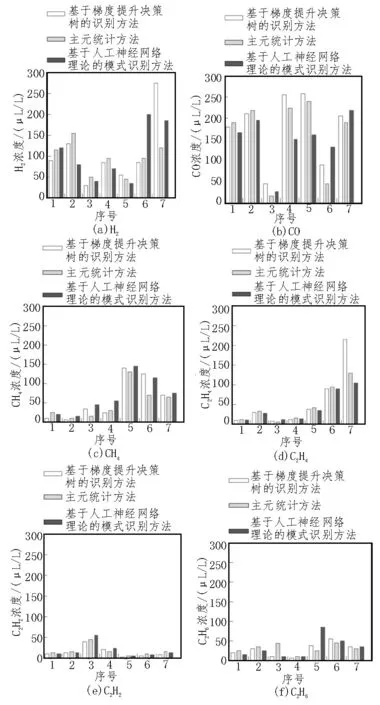
图2 三种方法识别结果对比分析

由图2（a）可知，使用基于主元统计方法在第7 次测试时，与实际值相差最大，最大误差约为150 μL/L；使用基于人工神经网络理论的模式方法在第6 次测试时，与实际值相差最大，最大误差约为125 μL/L；使用基于梯度提升决策树的方法在7 次测试情况下，均与实际值一致，误差为0。

由图2（b）可知，使用基于主元统计方法在第6次测试时，与实际值相差最大，最大误差约为40 μL/L；使用基于人工神经网络理论的模式方法在第4 次测试时，与实际值相差最大，最大误差约为110 μL/L；使用基于梯度提升决策树的方法在7 次测试情况下，均与实际值一致，误差为0。

由图2（c）可知，使用基于主元统计方法在第6 次测试时，与实际值相差最大，最大误差约为45 μL/L；使用基于人工神经网络理论的模式方法在第4 次测试时，与实际值相差最大，最大误差约为32.9 μL/L；使用基于梯度提升决策树的方法在第5 次测试时，最大误差为0.7 μL/L。

由图2（d）可知，使用基于主元统计方法和基于人工神经网络理论的模式方法均在第7 次测试时，与实际值相差最大，最大误差分别为90、120 μL/L；使用基于梯度提升决策树的方法在第3 次测试时，最大误差为0.05 μL/L。

由图2（e）可知，使用基于主元统计方法在第7 次测试时，与实际值相差最大，最大误差为10.2 μL/L；使用基于人工神经网络理论的模式方法在第3 次测试时，与实际值相差最大，最大误差为25 μL/L；使用基于梯度提升决策树的方法在7 次测试情况下，均与实际值一致，误差为0。

由图2（f）可知，使用基于主元统计方法在第3 次测试时，与实际值相差最大，最大误差为38.5 μL/L；使用基于人工神经网络理论的模式方法在第5 次测试时，与实际值相差最大，最大误差为33.1 μL/L；使用基于梯度提升决策树的方法在7 次测试情况下，均与实际值一致，误差为0。

通过上述分析可以看出，采用该文所提的基于梯度提升决策树的气体传感阵列识别方法，对实验中样本数据进行识别，得到的结果均优于主元统计方法、基于人工神经网络理论的模式识别方法，充分验证了所提方法的有效性，说明该文方法在实际应用中具有一定优势。

3 结束语

由于气体传感阵列中存在敏感数据，使用主元统计方法、基于人工神经网络理论的模式识别方法识别的结果存在较大误差。因此，提出基于梯度提升决策树的气体传感阵列识别方法。该方法主要以梯度提升决策树作为主体算法，借助scale 函数构造归一化模型，标准化预处理敏感数据，缩小敏感数据与其他数据的差异，并通过决策树构建最终的识别模型，提升识别的精度。实验中以变压器油中溶解气体为例，对气体传感阵列进行深入识别。实例结果表明，该方法精度高，稳定性好。

虽然该文方法在现阶段具有一定可行性，但仍存在一些有待进一步研究的问题：不同方向气敏传感阵列对气体的响应存在一定不同，只选取气敏元件阵列对气体浓度的响应作为特征量。在下一步工作中可深入研究不同布置方式对气体浓度的影响。