基于STM32 和模糊免疫PID 算法的电机调速系统设计

沈学锋

（1.山东石油化工学院，山东 东营 257061；2.中国石油大学（华东），山东 青岛 266580）

作为电子机械设备中使用较为广泛的器件，直流电机具有良好的调速性能。传统的直流电机调速方法使用PID 控制[1-2]，该控制方式原理简单，同时硬件实现的成本较低，适用于调速精度较低的工业系统中。在现代工业的生产过程中，通常被控制对象不是线性变化的，一般会受到综合因素的干扰，这样其特性以及相关的技术参数会受到影响，控制系统也被看作是非线性和时变的系统。因此，使用传统的PID 控制算法无法对电机进行实时调速，电机调速效果变差进而影响工业生产过程的效率。

模糊免疫算法将模糊理论和PID 控制算法相结合，使用模糊理论进行相关规则条件的制定，可以表征相应的执行规则和操作使用模糊集合，然后根据这些模糊集合建立对应的指令库。由编写的程序对控制系统的输出进行判断，进而确定执行的相应规则，完成PID 参数的最优化选择。模糊免疫PID 算法可以实时地对电机进行调速，克服了传统PID 算法实时性差、无法自我调整的缺陷[3-4]。文中使用STM32 开发板作为硬件平台，使用模糊免疫PID 算法进行直流电机的调速，系统实时性强且运行更加稳定，具有一定的工程应用价值。

1 硬件系统架构

1.1 电路总体设计

该文设计的电机智能调速系统由STM32 单片机、直流电机、电机驱动芯片编码器等器件组成。电路总体设计框图如图1 所示。

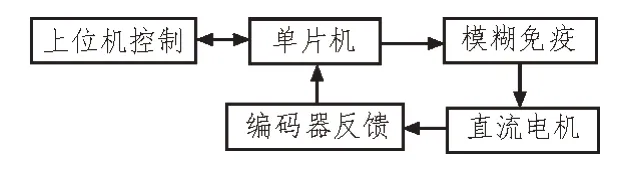
图1 系统总体设计框图

1.2 电机模块设计

所设计的电机模块使用的驱动芯片为IRS 21867，该芯片由英飞凌公司生产，并且专用于电机驱动这一功能[5]。该芯片可配置在高达600 V 的用电环境中，是一款高性能的MOSFET。IRS21867 芯片的输入兼容CMOS 引脚或者TTL 引脚的电平，兼容3.3 V和5 V 的电平逻辑协议。同时输出具有脉冲电流缓冲，有4 A 的拉电流和灌电流，驱动性能较强。由该芯片设计的驱动电路如图2 所示。

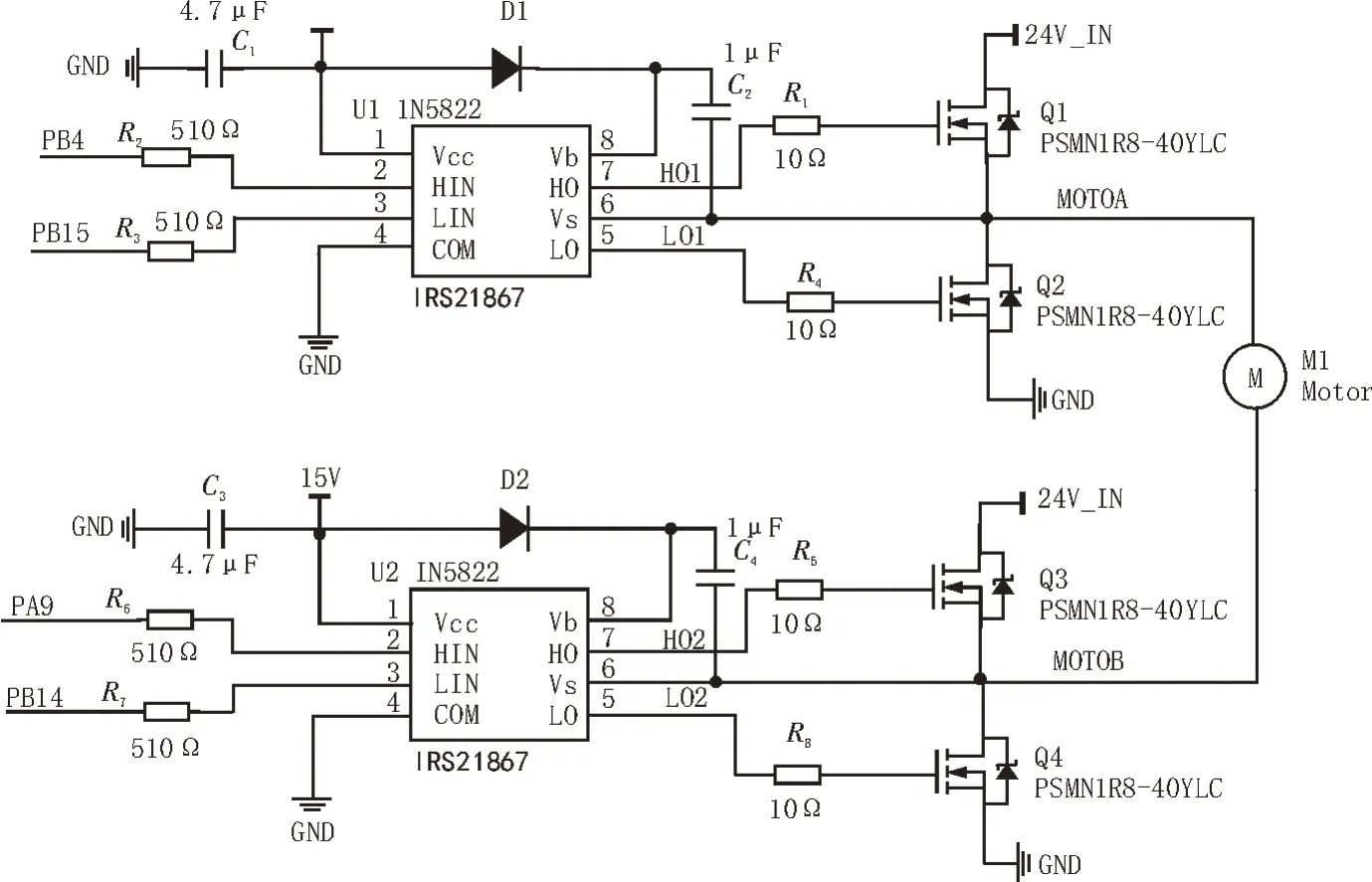
图2 电机驱动电路

1.3 STM32单片机电路设计

STM32 单片机可以运行算法程序，进而实现一定的逻辑。STM32 类型的单片机有诸多型号，根据该文外设数量以及使用需求最终选择了意法半导体公司生产的STM32F103C8T6 型号的单片机嵌入式系统。该信号嵌入式系统内核采用ARM Cortex-M3，位数为32 位，其内核工作频率最高可达72 MHz，芯片使用的封装类型为LQFP48，内部有程序存储器，容量高达64 kB。同时外设资源丰富，拥有两个12 位的高速模数转换器，有4 个16 位的计时定时器。此外还设有串口、SPI 等资源接口。该芯片的工作电压范围为2.2～3.7 V，工作温度范围为-40～85 °C，单片机电气性能稳定，耐用性强。单片机最小系统包括单片机芯片电路、时钟电路以及复位电路，该文设计的单片机最小系统电路如图3 所示。

图3 单片机最小系统电路

2 模糊免疫PID算法

2.1 免疫反馈算法

免疫反馈算法的概念最早来源于生物领域，生物领域的免疫系统由免疫器官、免疫组织、免疫细胞等结构组成。当生物个体遭受到病菌入侵时，免疫细胞会产生抗体对病菌体进行吞噬或者破坏。主要的免疫细胞分为免疫B 细胞和免疫T 细胞[6-8]。

免疫过程为当抗原入侵生物体时，抗原的信息会首先发送至免疫T 细胞，T 细胞对免疫B 细胞的数量进行调控。同时，T 细胞也分为增强T 细胞和抑制T 细胞。增强T 细胞是当抗原浓度变大时，该类型细胞会刺激B 细胞数量增多；抑制T 细胞是当抗原浓度减小时，该类型细胞会抑制T 细胞的数量。经过动态的刺激和抑制，免疫系统可以达到对抗原的快速反应。免疫系统的数学理论如图4所示。

图4 免疫系统数学理论

由图4 可知，假设t时刻的抗原数量为ε(t)，抑制T 细胞数量为Ts，增强T 细胞数量为Th。经过抗原刺激后，t时刻的抑制T 细胞和增强T 细胞数量分别为Ts(t)和Th(t)，则免疫B 细胞数量变化函数S(t)为：

在式（1）中，Ts(t)和Th(t)可以分别表示为：

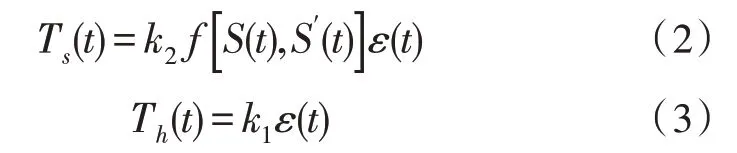
由此可知，反馈的关系式为：

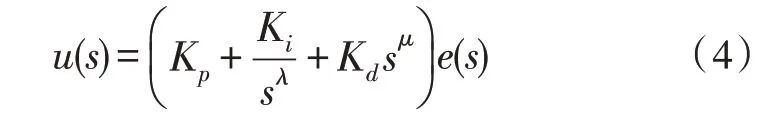
2.2 模糊控制原理

模糊控制器通常使用一系列的模糊规则作为决策表，通过查询模糊规则进而对控制量的数量大小进行判断[9-11]，其控制灵活，同时实时性较强。模糊控制过程如图5 所示。

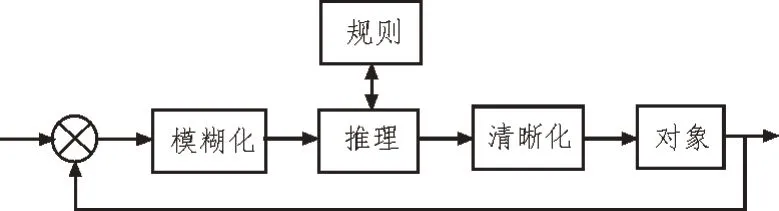
图5 模糊控制过程

2.3 PID控制器原理

PID 控制器根据其英文缩写可以看作是比例、积分和微分控制[12-13]。PID 过程是根据理论值和实际输出值之间的误差进行比例、积分和微分计算。传统的PID 控制流程如图6 所示。

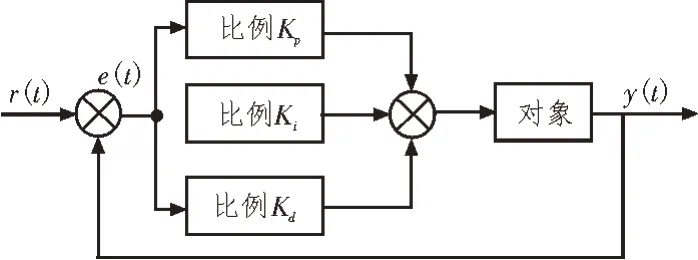
图6 PID控制过程

设定理论值为r(t)、实际输出值为y(t)，实际输出值和理论值之间的误差为e(t)，PID 控制的关系式如式（5）所示：

2.4 模糊免疫PID算法

模糊免疫PID 算法是将模糊规则和免疫反馈算法相结合[14]，同时使用PID 方式进行实现的一种控制方法，该文设计的算法实现形式，即模糊免疫PID 控制过程如图7 所示。

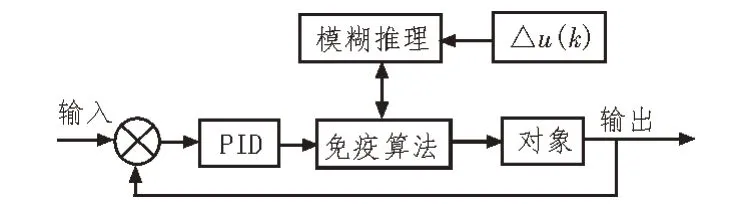
图7 模糊免疫PID控制过程

由图7 可知，文中算法由三个主要功能单元组成，使用免疫控制算法对被控对象进行控制，同时建立模糊推理规则对算法进行实时更新。

设免疫算法模块控制器比例增益为kp，由免疫算法的推导过程可知：

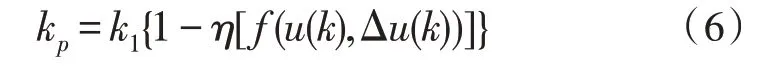
则免疫算法模块的输出为：

因此，加入模糊免疫算法后，进行更新的PID 算法公式应为：

基于上述算法流程对单片机进行编程，算法流程如图8 所示。

图8 算法流程

3 系统功能测试

3.1 算法稳定度仿真

通常情况下，PID 系统会受到各种各样的干扰，而系统对干扰的抵抗性能是算法的重要指标之一。因此，对该文算法稳定度进行测试是有必要的[15-16]。

首先假定一个二阶的传递函数，输入为阶跃信号，然后验证系统在阶跃响应控制中的性能。对比常规PID 算法以及该文所设计的PID 算法，算法结果如图9 所示。

图9 算法结果

如图9 所示，该文设计的模糊免疫PID 函数在控制过程中所具有的响应速度较快、波动幅度较小，说明该算法抵抗干扰的性能较强。

3.2 干扰实验仿真

在干扰实验中，为了测试PID 算法的性能，在实验中加入5 次脉冲信号进而对其进行误差测试，最终的控制测试参数如表1、表2 所示。

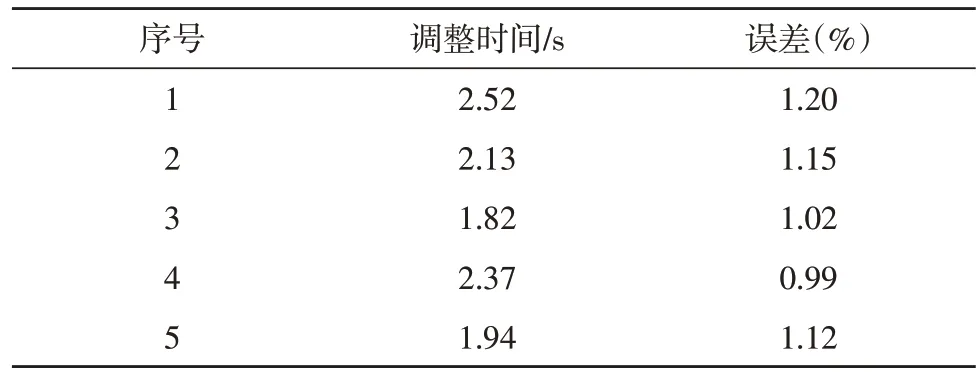
表1 常规PID算法干扰实验仿真结果

由表1 和表2 的实验结果可以看到，常规PID 算法中的最小干扰调整时间为1.82 s，最大误差值为1.20%。而该文算法干扰最小调整时间为0.59 s，最大误差值为0.82%。可见常规PID 算法平均调整时间要明显大于模糊免疫PID 算法，同时调整误差值也更小。这也进一步说明了模糊免疫PID 算法比常规PID 算法调整时间更短，抗干扰能力更强。

表2 该文算法干扰实验仿真结果

3.3 电机转速误差测试

为了验证该文设计的模糊免疫PID 算法在电机速度调节中的性能，该文对电机转速的误差进行仿真测试。

由表3 可以看出，该文电机转速调节误差均在1%以内，说明该算法可以对电机的转速进行准确调节。表明该文算法的综合性能良好，达到了设计的目的。

表3 转速调节

4 结束语

使用传统的PID 控制算法无法对电机进行实时的调速，算法精度较差。模糊免疫算法将模糊理论和PID 控制算法相结合，使用模糊理论进行相关规则条件的制定，进而确定执行的相应规则，完成PID参数的最优化选择。该文使用STM32 开发板作为硬件平台，并使用模糊免疫PID 算法进行直流电机的调速。实验结果表明，该文设计的系统在稳定性及抗干扰性上均有良好的表现。在转速测试中，电机转速调节误差均在1%以内，说明该算法可以对电机的转速进行准确调节，系统实时性强且运行稳定。