仿生灵巧机械手设计与自适应控制
杨昆明,周 欣,王 鹏,王晋鹏
(西安航空学院机械工程学院,陕西西安 710077)
随着科学技术的发展,机器人已应用于国民经济的各个领域。仿生机械手作为仿生机器人的末端执行器,其运动应该更迅速,灵活性应该更高[1-2]。为使仿人机械手实时作业时运动能够更加精细准确,提出采用神经网络作为补偿器,对其逆运动学进行求解,建立了其运动轨迹与力矩之间的映射关系,对机械臂动力学模型非线性和参数不确定性进行轨迹跟踪控制,且通过仿真实验,对机械手关节产生的精度误差进行评估、修正、验证[3-8]。
鉴于仿生机械手工作时精度要求高,智能控制算法在仿人机械手这一方面研究又较少[9-15]。该文使用径向基函数神经网络对其进行控制,在推导仿生机械手动力学模型的基础上,得到解决外界扰动引起的精度、实时性等问题的自适应控制方法。
1 仿人机械手设计
1.1 人手结构特性分析
人的手,无论是左手还是右手,手部骨骼都分为腕骨、掌骨、指骨三大部分。指骨有五种类型,分别为拇指、食指、中指、无名指和小指。整个手掌由五根掌骨组成,靠肌肉组织连为一体,作为机械结构设计,可以将其作为一整体来看待。指骨除拇指外其余四根手指结构,除尺寸大小外,结构完全相同,都具有基节、中节、末节三个关节,拇指只有基节、末节两个关节。人手的每个手指可以看成是一个小的关节型机器人,因此单根手指的结构与关节型机器人相似,这种结构特点为研究机械手提供了方便[16]。
1.2 仿生结构设计
仿人机械手整体结构设计分为手掌和手指两部分,根据人手骨骼结构特点,设计了保留人手大部分生物学特征的仿生机械手。仿人机械手整体结构紧凑,与人手外形相似。由于该文所研究的仿人机械手各个指关节可以单独运动,且五个手指基本结构是一致的,所以这里仅就其中有代表性的食指进行研究。由于人手在抓握物体时,末关节基本不动,对人手指骨进行简化设计,把中关节和末关节设计成一体,其包括两个自由度,即基关节与掌骨(五根掌骨看作一体)连接,基关节与中关节相连[17]。
2 手指动力学建模与分析
机器人动力学模型是进行机构设计、运动规划与控制的基础,机械手指又是一个强非线性、多耦合系统,所以为了使仿生机械手在应用中能对环境有较强的适应性和抗干扰能力,需要对仿生机械手进行动力学控制[18-19]。
仿人机械手在抓取物体时,手掌、手指和物体之间是一个高度复杂的强非线性、多耦合系统,直接进行仿人机械手动力学建模难度非常大,为了研究方便,一般都采用简化的方式来对机械手进行建模[20-21]。该文将所设计的仿生机械手单手指简化为二连杆模型,如图1 所示,基于拉格朗日方法建立其动力学模型。
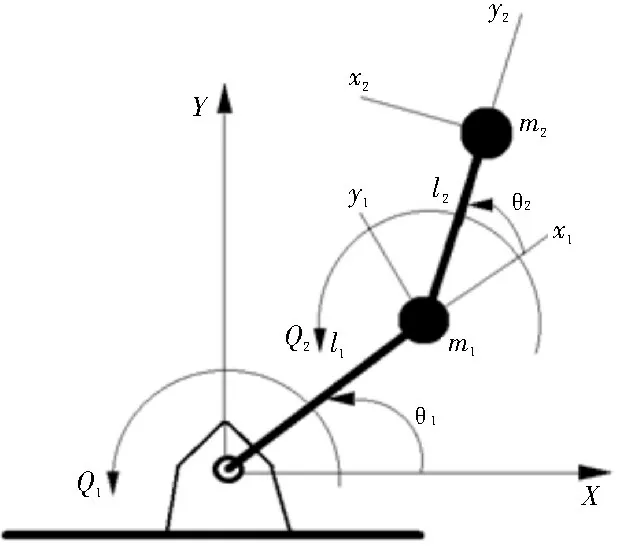
图1 机械手关节连杆
拉格朗日函数是以动能与势能之差定义的,如式(1):

应用拉格朗日函数可以求得具有n个关节的串联机器人系统的拉格朗日运动方程,如式(2):
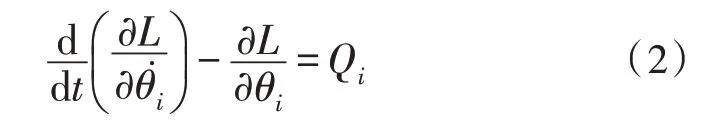
式中,i=1,2,…,n,Qi是驱动θi的相应广义力,该力为第i个广义坐标θi的一个虚位移做功。
对于n根连杆串联的机械手,其运动方程能以矩阵形式建立,如式(3):
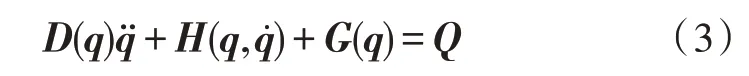
假设两连杆的质心位于连杆的末端位置,关节处的电动机是无质量的,取θ1、θ2为系统的广义坐标,质量m1和m2的全局位置矢量为:
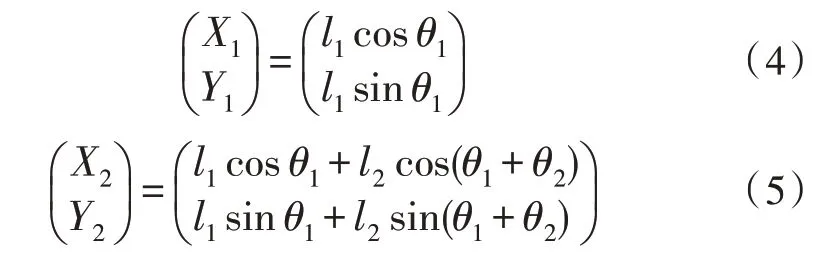
机械手指的动能、势能为质量m1和m2的动能、势能之和,即:
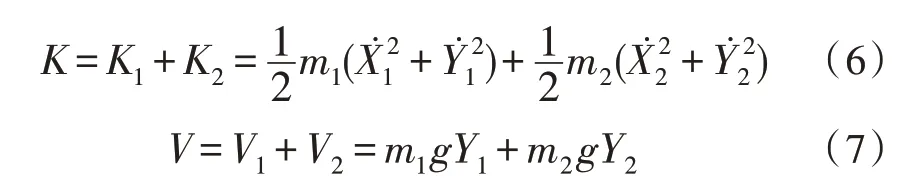
由式(2)可知二连杆拉格朗日函数为:
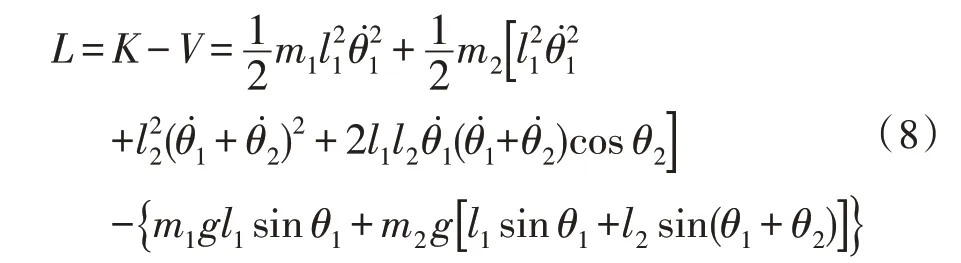
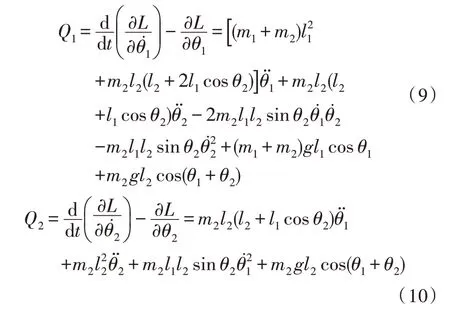
3 控制仿真分析
在机械手作业中不仅要考虑系统误差,还有各组成模块之间的摩擦与扰动等不确定因素也会影响到机械手最后的抓取精度。所以,为了适应各种不同的抓取环境和对象,对所设计的机械手的适应性和灵活性提出了很高的要求,依据上述推导的动力学模型,针对误差扰动信号ω上界未知这一条件进行自适应控制。当前,人工智能算法被广泛地应用到现代制造业领域中,其中神经网络算法就是一种十分重要的仿生算法。由于神经网络算法模拟人体神经工作原理,且具有良好的逼近特性和全局寻优性能,所以可以采用RBF 神经网络实现未知函数f(x)的逼近。
3.1 RBF神经网络设计原理
RBF 神经网络算法为:
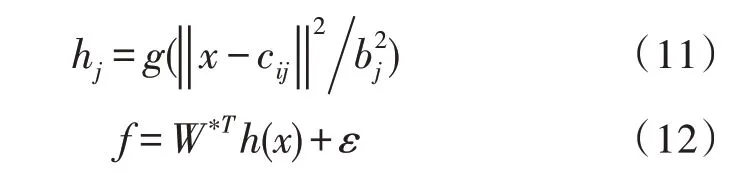
式中,x为网络的输入;i为网络的输入个数;j为网络隐含层的第j个节点;h=[h1,h2,…,hn]T为高斯函数的输出;W*为网络的理想权值;ε为网络逼近误差,|ε|≤εN。
采用RBF 逼近未知函数f(x),取神经网络的输入为x=[x1x2]T,则径向基神经网络的输出为:

3.2 控制器设计
首先,定义跟踪误差,如式(15):

式中,qd(t)为理想指令;q(t)为实际角度。
再定义滑模函数,如式(16):
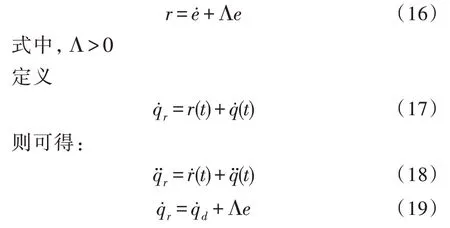
将式(17)、(18)代入式(3)中,并根据n关节机械臂系统模型设计控制器为:
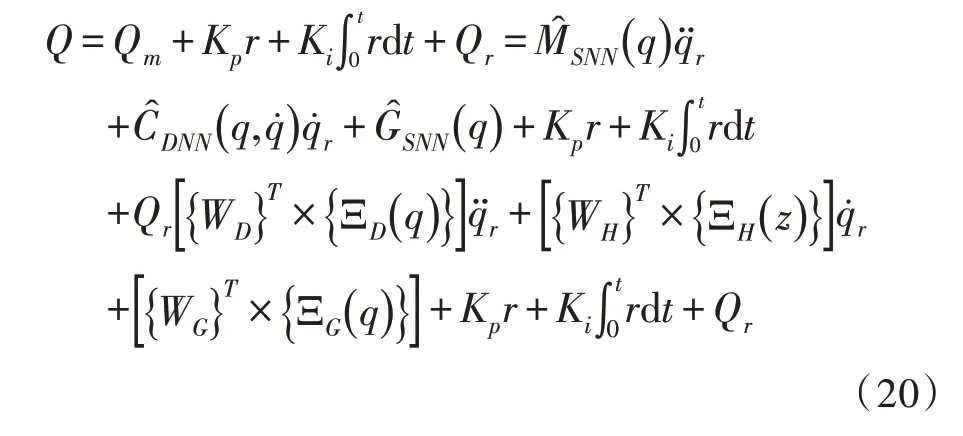
式中,Kp>0,Ki>0。
名义模型的控制率为:
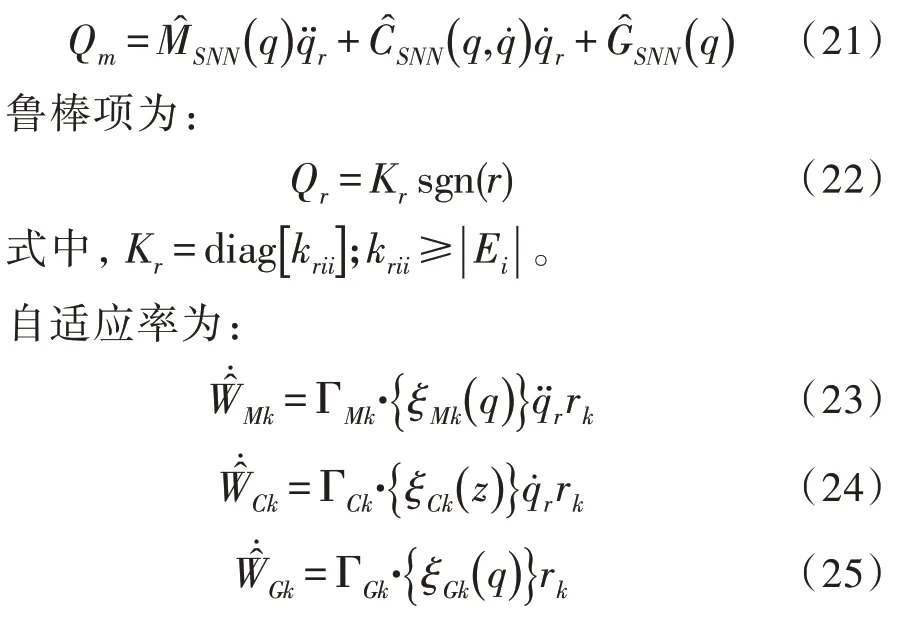
式中,k=1,2,…,n。
3.3 仿人机械手指关节控制仿真
为验证该文所设计算法的可行性,利用Matlab软件对仿生机械手食指系统进行仿真分析。该仿真实验主要是验证第二关节自适应算法的实用性和有效性,该仿真实验采用基于RBF 神经网络逼近f(x),并估计未知参数。由式(3)可得,取p=[0.000 5 0.000 25 0.000 25 0.01 0.005]T,被控对象初始位置为,理想位置指令为ql1=0.5 sin(πt),ql2=sin(πt),控制器参数Kp=Ki,仿真结果如图2、图3 所示。
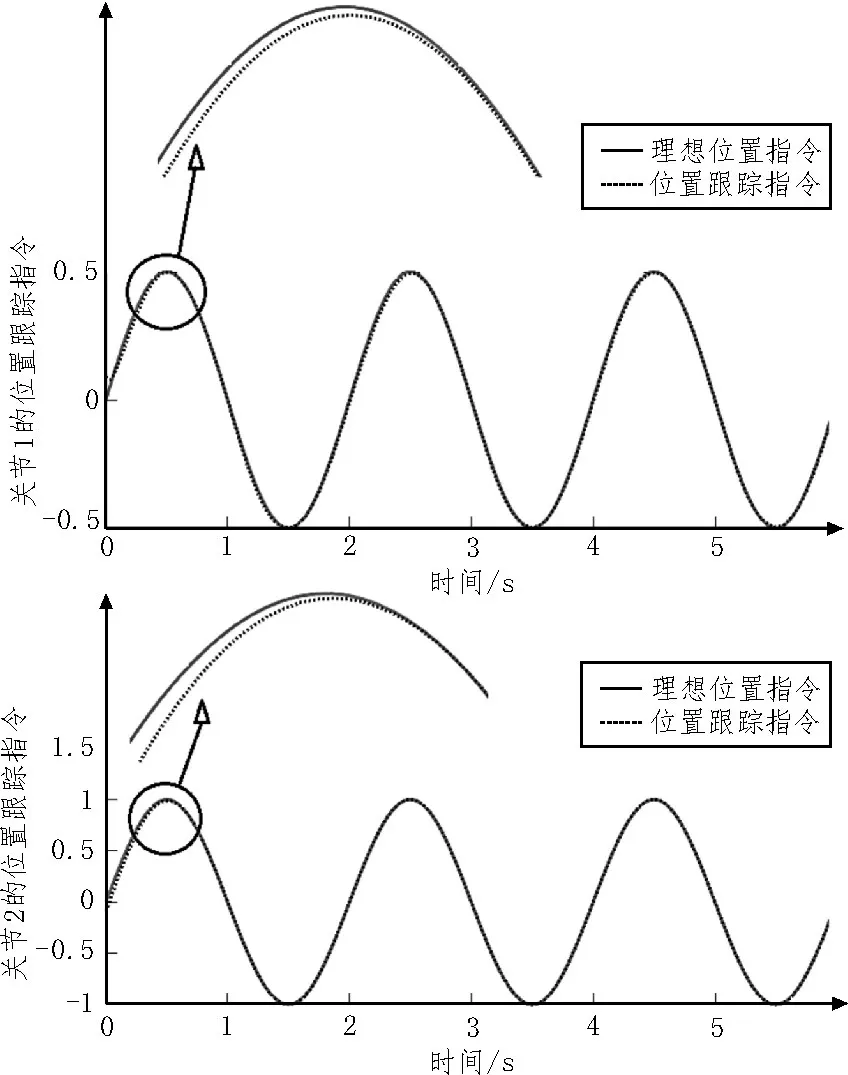
图2 关节1和2的位置跟踪
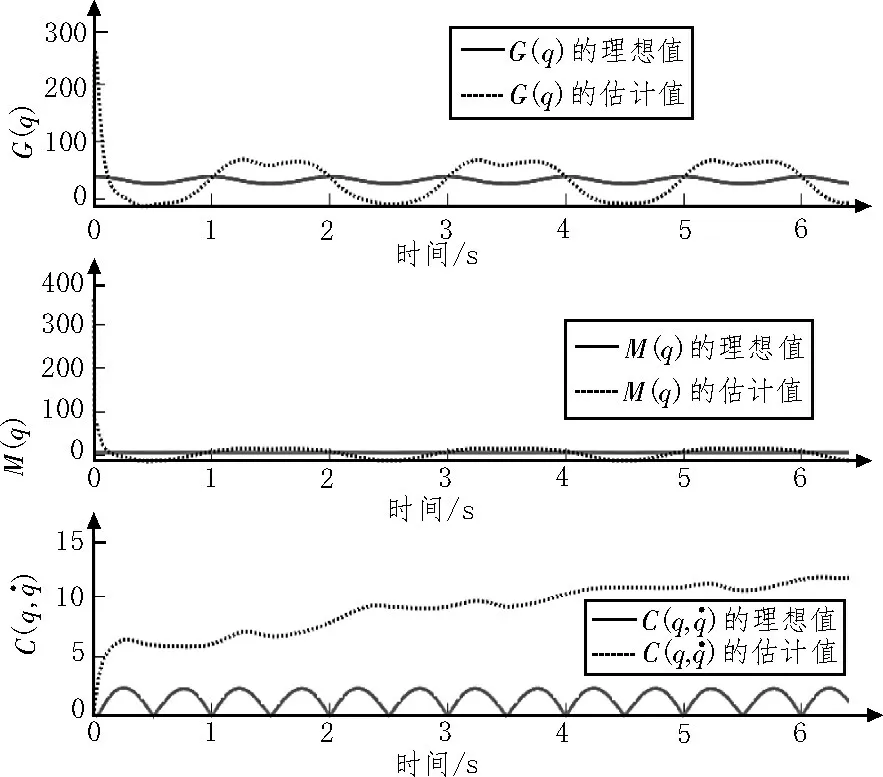
图3 G(q)、M(q)和的逼近
根据仿真结果进行分析,图2 为关节1 和关节2的位置跟踪,图中实线为理想位置指令,虚线为在神经网络模型作用下得到的位置指令,从图2 可以看出,机械手系统的期望运动轨迹能够被快速跟踪到,在不到1 s 的时间内,所设计的神经网络模型就可以很好地跟踪到理想轨迹上,可以看出误差随着时间变化逐渐趋近于0,可见该方法鲁棒性能好,跟踪精度高,收敛速度快,且对具有良好的逼近效果。
4 结论
该文在机械灵巧手的自适应、实时性方面做了以下工作:
1)利用仿生学原理通过对人手骨骼结构的分析而设计出仿人五指机械手,体现了仿生的要求,仿人机械手整体结构紧凑,外形与人手相似。
2)基于拉格朗日方程求解仿生机械手动力学模型。采用径向基函数神经网络对机械手双关节手指进行控制,并利用Matlab 软件,对设计的控制方法进行仿真验证。由仿真结果可得,所设计的控制器可有效提高灵巧机械手控制系统的跟踪精度、鲁棒性和自适应性。

