电池储能系统参与用户侧削峰填谷的鲁棒优化调度策略

陈睿彬，陆玲霞，包哲静，于淼

(浙江大学电气工程学院，杭州市 310027)

0 引 言

为尽早实现碳达峰、碳中和目标，具有强随机性波动性的新能源得到飞速发展，使得电网内负荷峰谷差现象日趋严重[1]。为提高电网运行的稳定性与安全性，有必要引入相应的削峰填谷措施。仅依靠多种能源互补互济的调控方式往往存在局限性，新能源的波动性与随机性一方面会给电网的稳定性与安全性造成挑战，另一方面又对能源自身的消纳不利，因此在电网中配置储能以提高系统调控能力是有效且必要的举措[2-4]。文献[5]指出，结合能源互联网的源-网-荷-储协调调度，是实现新能源高效利用与电网负荷削峰填谷的有效措施。

传统调峰方法通过观测电网负荷波动并以此调节网内发电机组的输出功率，要求发电机组具备较高的调峰容量，而机组频繁启停也造成了燃料资源的浪费。与之相比，从负荷侧进行调控的大规模电池储能系统在削峰填谷方面的优势更加显著[6]。一方面，电池储能系统(battery energy storage system，BESS)最优调度领域已有大量研究可供应用；另一方面，电池梯次利用前景广阔[7-9]，电池储能系统的建设成本已得到显著降低。文献[10]通过比较梯次利用电池和新电池的成本、使用寿命，研究了相应储能系统效益与电池收购价、峰谷电价差等因素的关系。在此类研究的基础上，电池储能系统的应用范围及经济性得到了较大程度的发展，因此在更广阔的应用领域，相关电池储能系统参与调峰的研究得以开展。文献[11]提出一种利用电动汽车电池作为储能平台参与微电网调峰的控制策略，通过为微电网内的可再生能源提供缓冲以提高微电网运行效率。文献[12]提出一种利用储能电站的削峰填谷优化调度方法，在规模化分布式光伏并网所引发的系统调峰需求下，令总体净负荷方差最优化。

然而，仅根据负荷、可再生能源出力等的预测值所得到的储能调度策略在应对源荷波动性上仍有不足，应用鲁棒最优策略应对源荷波动不确定性是一种有效的方法[13-14]。已有众多研究专注于储能调度的鲁棒最优策略，以应对源荷在不同场景下的不确定性。文献[15]提出一种考虑风电不确定性的热-电耦合微能源系统多目标鲁棒规划方法，同时考虑储能调度的鲁棒优化与多目标优化问题。然而与之类似的研究都局限于线性的形式，或是要求对非线性部分进行线性近似，造成不同程度的误差，而且并非所有的非线性优化目标都适合被线性近似。文献[16]列举了不同的削峰填谷评价指标并比较了各种指标的特点和适用场景，其中不乏非线性的评价指标。而在考虑非线性优化目标的储能调度研究中，对鲁棒优化的关注较少[17]。文献[18]考虑光伏出力和负荷的不确定性，采用特殊序列集合方法对非线性模型进行分段线性化，尽管结果优于粒子群算法，但是转化成的混合整数线性规划问题会随分段数量增加而规模增大。与此同时，此类方法不能应对决策变量取值范围直接受不确定因素影响的情况。

基于此，本文从鲁棒二次优化问题着手，研究非线性优化目标、约束条件涉及不同阶段变量的鲁棒优化问题解法在储能调度中的应用。传统列和约束生成(column-and-constraint generation, C&CG)算法主要用于解决多阶段鲁棒线性优化问题[19]。本文在已有研究成果的基础上，改进该算法以解决上述类型的鲁棒多目标优化问题并加以论证。最后，通过改进的算法解决一个以净负荷方差为优化目标、考虑光伏出力和负荷不确定性的储能最优调度问题，验证算法的有效性。

1 储能参与用户侧削峰填谷的优化模型

1.1 优化目标

本文在考虑储能参与用户侧削峰填谷的同时，选取光伏发电作为具有代表性的不确定性新能源并入同一母线。一方面，电力系统运行要求安全平稳，需要对储能调度进行优化，使储能调度后的用户侧净负荷曲线相对平缓，以减少备用机组频繁启停，并且需要考虑到负荷、新能源在一定范围内的任意波动；另一方面，需要考虑储能调度的成本，使维护成本和电价总和在可接受的范围内。

1.1.1 削峰填谷评价目标

考虑到需要使优化用户侧净负荷曲线更加平缓，更适合将用户侧净负荷方差作为削峰填谷评价指标，以表示净负荷在指定时间内的总体离散程度。这能够在兼顾用户侧净负荷峰谷差的同时，降低总体波动程度。

(1)

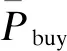
1.1.2 经济目标

向外部电网购电与售电的总电价是经济目标的主要组成部分，如式(2)所示：

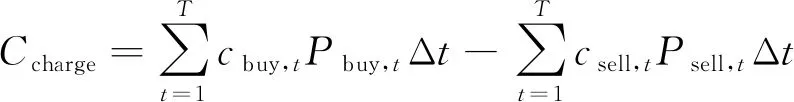
(2)

式中：Ccharge表示向外部电网购电与售电的总电价；cbuy,t与csell,t分别表示购电与售电的电价，当模型采用分时电价时，不同时刻t下的电价将依据地方具体电价政策随时间改变；Δt表示步长。

本文考虑的维护成本包括储能设备的维护成本和发电设备的维护成本，如式(3)所示：

(3)

式中：Cmaint表示总维护成本；mpv为光伏设备的维护成本系数；Ppv,t表示t时刻光伏设备出力；mb为储能设备维护成本系数；Pb+,t表示t时刻储能设备的充电功率；Pb-,t表示t时刻储能设备的放电功率。

1.2 约束条件

1.2.1 电池储能系统约束

电池储能系统输入输出功率存在上下限：

(4)

式中：Pb+,max表示电池储能系统充电功率上限；Pb-,max表示电池储能系统放电功率上限。电池储能系统应尽可能降低内耗与维护成本，约束Pb+,t•Pb-,t= 0确保同一时刻充电放电功率至少一个为0。

电池储能系统荷电状态(state of charge, SOC)须运行在一定的区间。一方面，是为了延长电池的使用寿命；另一方面，是为了保证留有足量的备用储能以应对电力系统故障[20]：

(5)

式中：Et表示t时刻电池储能系统储存的能量；ηc表示能量转化效率；SOC,t表示电池储能系统荷电状态，需要运行在有限的区间，电池储能系统才能有预期的性能；SOC,min、SOC,max分别表示该区间的下界、上界；Erated表示电池储能系统的总额定容量。

除此之外，电池储能系统储存的能量在一个优化周期的始末态需要相等，这使电池储能系统储存的能量对任意一个优化周期的影响等同，邻近的优化周期可以前后衔接。

SOC,1=SOC,T

(6)

1.2.2 用盒式不确定集表述的不确定性

当前已有技术可以实现较低误差的负荷预测[21]，可据此使用盒式不确定集近似表述概率分布复杂或未知的不确定量。在本文中，负荷与光伏出力的不确定性用盒式不确定集加以表述：

Ppv,t,min≤Ppv,t≤Ppv,t,max

(7)

Pload,t,min≤Pload,t≤Pload,t,max

(8)

式中：Ppv,t,max和Ppv,t,min分别表示用户侧光伏并网输出功率的上界和下界；Pload,t表示用户侧负荷；Pload,t,max和Pload,t,min分别表示用户侧负荷的上界和下界。

对于时刻t，根据预测结果，不确定的用户侧光伏并网输出功率Ppv,t存在上界Ppv,t,max与下界Ppv,t,min，不确定的用户侧负荷Pload,t同样在上界Pload,t,max与下界Pload,t,min间波动。因为无法预知源荷的实际值，所以储能调度决策变量对于区间内的任意可能波动都必须是可行的，亦即无论源荷的实际值在区间内取什么值，其他的约束条件都是满足的。

1.2.3 功率等式约束

为简化模型，忽略电网损耗，时刻t用户侧与外部电网交互的能量由光伏发电量、用户侧总负荷和电池储能系统的充放电决定。

Pbuy,t-Psell,t=Pload,t-Ppv,t+Pb+,t-Pb-,t

(9)

1.3 鲁棒优化问题的构造

由式(1)根据削峰填谷评价目标构造式(10)，用以表示净负荷方差。该指标越大，净负荷波动越显著。

f1=Cvar

(10)

式中：f1表示鲁棒优化问题的第一个优化目标，是一个非线性凸函数。

由式(2)与式(3)根据经济目标构造式(11)，用以表示用户侧总用电支出。

f2=Ccharge+Cmaint

(11)

式中：f2表示鲁棒优化问题的第二个优化目标，是一个线性函数。

令：

(12)

式中：y、u、x分别为通过已定义的变量分别构造鲁棒优化问题的第一阶段决策变量、不确定变量和第二阶段决策变量；Y、U、F(y,u)分别为其取值范围。

由式(4)至(9)的约束条件可知，y的取值范围Y集是一个独立于u、x的多面体，u的不确定集U集是一个独立于y、x的有界多面体，x的取值范围F(y,u)是一个由y、u线性决定的多面体。

引入ε-约束法以处理多目标优化问题，可构造如下鲁棒优化问题：

(13)

式中：ε1为使用ε-约束法所需要提前给定的具体数值，用于将优化目标f2转化为鲁棒优化形式的ε-约束，表示当u在U集内任意波动时，优化目标f2所能允许的最大值。

储能调度的目的在于找到一个调度计划，对于负荷、光伏在不确定集内波动的任意一种可能，都能够满足保证系统安全的约束条件，能够将系统的经济开销控制在一定范围内，且该调度计划能够使最不利可能性下的净负荷方差达到最小。

式(13)中的ε-约束表示，采取了一个储能调度计划y后，若遭遇了对f2最不利的u，且x按最小化优化目标f1的原则取值，该储能调度计划y能保证在任意可能性下f2仍能满足≤ε1的约束。原因在于：

1)u的具体波动是不受控制的，一旦给定波动的不确定集，便不能以任何方式约束不确定集。因此u的约束能够限制y的取值范围，反之则不能。

2)对于一个确定的储能调度计划y，虽然对f1和f2最不利的u一般不同，但是x∈F(y,u)并不会在y、u确定的情况下分别对f1和f2有两个不一样的取值。因此约束中f2的x参数不能与f1相冲突，仅可存在一个取值标准，约束中f2最终可以表示为y、u的函数h(y,u)。

2 改进型列和约束生成算法

2.1 列和约束生成算法原理及改进方案

定义如下线性鲁棒优化问题：

(14)

根据文献[19]的假设， 第一阶段决策变量可行域Y集是一个独立于不确定变量u、第二阶段决策变量x的多面体，不确定集U集是一个独立于第一阶段决策变量y、第二阶段决策变量x的多面体，第二阶段决策变量可行域F(y,u)是一个由y、u确定的多面体。c、b均为常量，因此优化目标为线性函数。当问题中存在上述形式以外的约束条件使Y集、U集中并非所有的元素都能保证第二阶段决策存在可行解，亦即当u的不确定性能够影响y的取值范围使之在算法过程中变化，传统C&CG算法就不再适用，所得的解会出现难以预计的错误。而式(13)的约束正属于此类情况，除了电池储能系统自身的功率与SOC相关约束，要求在不确定集中任意可能性下的经济开销均在给定范围内，同样会对调度计划的可行域造成影响。某一电池储能调度计划即使满足电池储能系统充放电功率约束，只要存在一种可能的不确定场景令第二阶段决策无解，那么原算法的子问题 (subproblem，SP)寻找最不利场景的过程就会因为略去所有令第二阶段决策无解的不确定场景而失败。当鲁棒优化问题涉及多个优化目标、更复杂的多变量非线性约束时，这个问题会更加严重。

原算法的核心思想是将原始问题的不确定集U集松弛为其中的数种场景，枚举这些场景以求取仅考虑这些场景的鲁棒最优解，也就是原算法的主问题(master problem，MP)。MP因此是原始问题的一个松弛问题。当MP未能考虑足够的场景，即未能实现精确松弛，因为松弛问题约束更宽松，所以MP所得的目标函数值一定不大于原始问题的目标函数最优值。而原算法的SP则是将MP所得的y作为SP的输入，在不确定集U集中求取对优化目标最不利的一个场景u，并将其加入MP需要考虑的数种场景中，逐步实现不确定集的精确松弛，从而实现MP对原问题的精确松弛。因为SP所使用的y是MP的解，劣于原始问题的最优解，所以SP所得的目标函数值一定不小于原始问题的目标函数最优值。反复迭代，SP将不断向MP补充需要考虑的场景，直至MP所得的目标函数值与SP所得的目标函数值相等。此时由夹逼定理可知，MP所得的目标函数值等于原始问题的目标函数最优值，MP所考虑的数种场景已经实现了对原始问题不确定集的精确松弛，仅考虑这些场景的MP实现了对原始问题的精确松弛。

然而原算法的SP仅能在不确定集U集中求取对单个优化目标最不利的场景。不仅如此，如果SP的约束条件导致SP无法在完整的不确定集U集上取值，那么算法就会出错，而这正是上文所述问题会导致的情况。

但如果在原算法的基础上扩充Step 3，引入可以同时运算的多个不同目标的SP，就能够完善该不足。对式(12)、(13)所示的一类鲁棒优化问题，本文对C&CG算法的应用与改进如下：

(15)

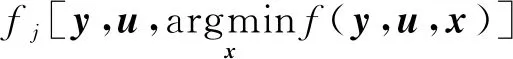
Step 1：设置Blower=-∞，Bupper=+∞，分别代表最优值的下界和上界，并给出允许的最大误差e。定义离散集V，用于表示不确定集的一个离散子集，任取U的一个顶点作为离散集V最初的元素，其大小初始化为sV=1。定义迭代计数k=1。

Step 2：求解MP。

(16)

式中：η表示临时变量。

与文献[19]不同，此处的MP要求求解器能够求解非线性规划问题。

Step 3：分别求解n+1个SP。

对∀1≤j≤n：

(17)

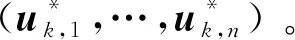
(18)

亦即分别求取对优化目标、复杂约束最不利的n+1个场景。

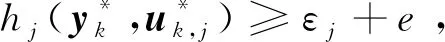
迭代计数k增加1。进入Step 2。

Step 5：返回当前的y*作为鲁棒优化问题的最优解，结束算法。

2.2 算法改进的原理及适用范围

定义如下的鲁棒优化问题：

(19)

式中：Y集是一个独立于u的有界多面体；U集是一个独立于y的有界多面体；g(y,u)、hj(y,u)是凸函数。

命题1：MP若已枚举了有界多面体U的所有顶点，则MP等价于原问题。

(20)

式中：pU表示有界多面体U的顶点数。若每个ui都表示有界多面体U的一个顶点，那么U中的任意一个元素可以表示为这些顶点的凸组合

命题2：在任意一次迭代中，有界多面体U存在一个顶点是式(19)所示原鲁棒优化问题的SP的解，且除非算法已满足结束条件，任意一次迭代中，至少存在一个SP不会得出先前迭代中离散集V中已存在的元素。

对∀1≤j≤n：

(21)

以及

(22)

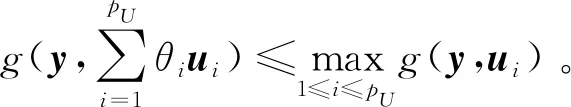
综上，对于式(19)所示的鲁棒优化问题总能通过上述算法得到收敛的解，最坏情况下，需要遍历不确定集U集的所有顶点。

结合式(10)至(12)，令：

(23)

(24)

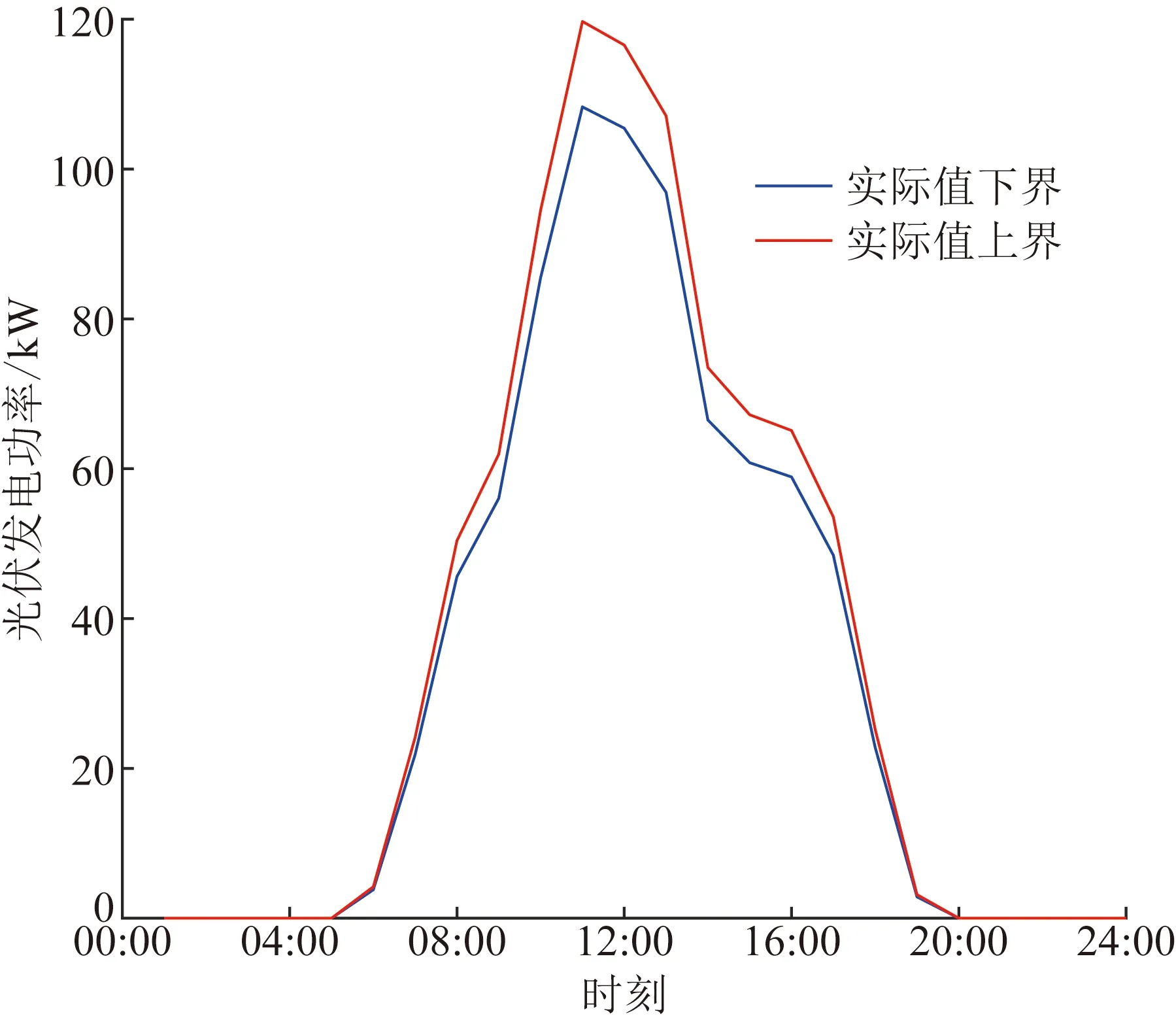
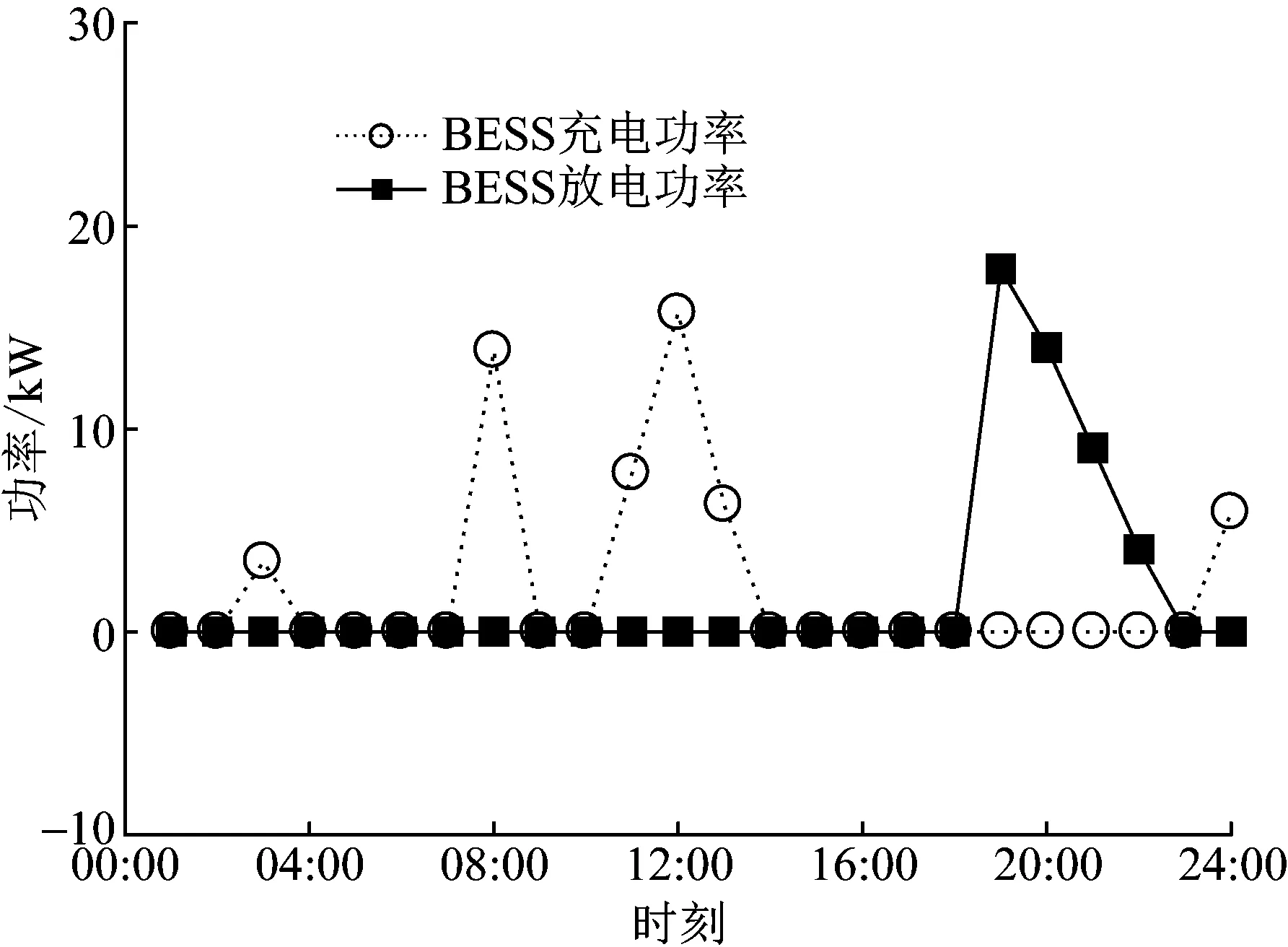
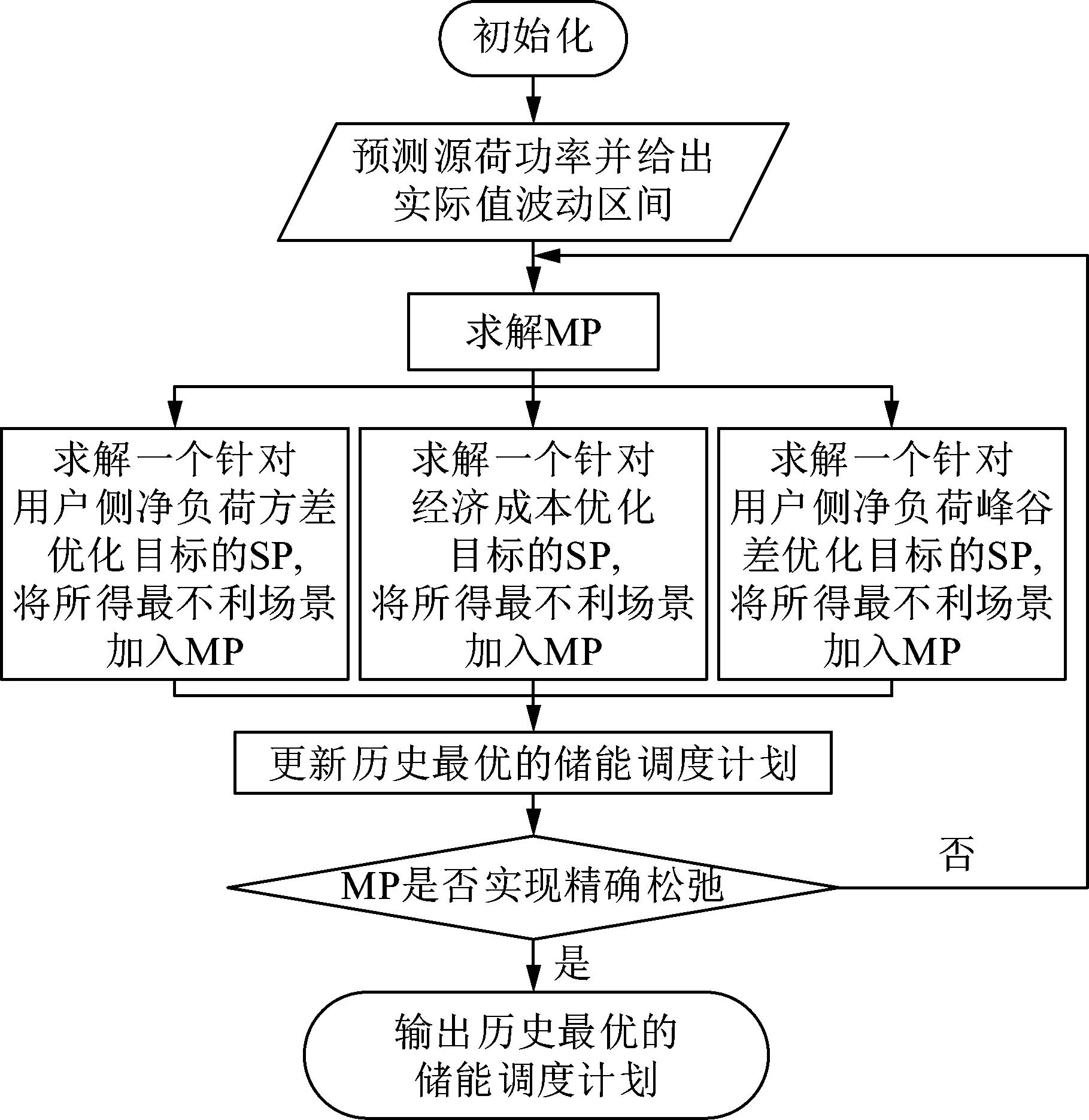
0≤csell,t

(25)

当式(1)中的cbuy,t与csell,t满足式(25)时，由式(9)和复合函数保凸运算的性质方可确保式(23)与式(24)是凸函数。综上，式(13)所构造的鲁棒优化问题，在满足式(25)时，满足命题1与命题2的要求，能够应用上文的算法求解。

3 算例分析

3.1 两优化目标的具体模型及其求解

为了验证本文所提策略的有效性，本文以MATLAB和Gurobi作为仿真求解工具，建立一个包含光伏不确定性和负荷不确定性的用户侧储能调度模型。该情景下，微电网中除了有不可控、只可预测的用户负荷，还有同样不可控、只可预测的光伏并网系统，允许在任意时刻向电网售电。以某居民区为例，当地居民用电分时电价如表1所示。

表1 某市居民生活用电电价

可用于调度的光伏储能、基站闲置备用储能等模型中的电池储能系统，采用梯次利用电池以确保经济上的可行性。参考文献[10]的研究，采用表2所示参数，仅代表一类常见的梯次利用电池所构建的电池储能系统在一般工况下所能表现出的性能与经济成本，并额外施加SOC约束避免深度充放电以延长使用寿命，留有安全裕量。

表2 电池储能系统参数

该模型的不确定性符合式(7)与式(8)的形式，具体如图1与图2所示。可行的储能调度计划必须确保，无论不确定集中的哪种场景发生，亦即无论源荷在此范围内怎样取值，所有约束条件都是满足的。表1中所示的参数符合式(25)的要求，因此该问题可以使用2.1节所述的算法进行求解，此时Step3包含两个并行的SP，具体实现流程如图3所示。

图1 光伏出力的不确定性

图2 用户负荷的不确定性

图3 两目标储能调度鲁棒优化流程图

当式(13)中的ε1取值为715时，亦即要求所得的储能调度计划实际执行后，对于在图1、图2所示区间内任意波动的光伏出力、用户负荷，都能保证满足各项约束且该日总体用电支出低于715元，并在此基础上尽可能降低净负荷曲线在该日的波动程度。

所得电池储能调度计划的鲁棒最优解如图4所示，与之对应的电池储能系统SOC变化如图5所示。对于光伏出力、用户负荷的波动，即使是最不利的可能性，都能够满足电力系统的各项约束条件。

图4 电池储能系统充放电功率(两优化目标，ε1=715)

图5 电池储能系统荷电状态(两优化目标，ε1=715)

执行该储能调度计划后，当对净负荷方差最不利的可能性发生时，光伏出力与用户负荷的波动均以最不利的形式发生，如图6所示。此时，无储能调度的净负荷曲线陡峭且上下波动程度较大，储能调度后起到了用户侧削峰填谷的效果，减小了净负荷曲线上下波动的程度。在该场景下，储能调度后净负荷方差为1 315 kW2，在所有可能性中是最大的，该日总用电支出629元，小于设定的715元。

图6 用户侧净负荷(对净负荷方差最不利的场景)

之所以上述情况下的总用电支出并没有达到最不利的715元，是因为最不利于净负荷方差的可能性与最不利于总用电支出的可能性并不相同。该问题需要考虑到两种最不利的可能性，因此不能在对净负荷方差最不利的可能性下完全牺牲总用电支出以更优化净负荷方差。而且在不同的储能调度计划下，两种最不利的可能性都会变得不同，需要分别通过算法求取，这也是改进后的算法需要多个SP的原因之一。

执行同一个储能调度计划后，当对总用电支出最不利的可能性发生时，储能调度在用户侧削峰填谷的同时兼顾优化经济成本，如图7所示。在该可能性下，当日总用电支出715元，达到了设定的限制，是所有可能性中最大的；而储能调度后净负荷方差为784 kW2，远小于最不利于净负荷方差的可能性。

图7 用户侧净负荷(对总用电支出最不利的场景)

这意味着如果按照一般的优化问题构建方法，把多个优化目标加权求和，就会忽视鲁棒优化问题中多个优化目标对应的多种最不利的可能场景。因此，在考虑鲁棒优化问题的帕累托最优时，应当避免加权求和不同量纲的优化目标构成新目标的做法，需要分别针对每个优化目标考虑对其最不利的可能场景，对经济成本目标最不利的源荷场景仅能用于评价储能调度在经济成本目标的效果，而不能用于评价削峰填谷目标，反之亦然。当确定了可接受的经济成本最大值ε1后，在此基础上最优的削峰填谷目标也就随之确定。

遍历可行的ε1，即可得到如图8所示的帕累托前沿。ε1取值为715所对应的储能调度计划，相对于完全偏向于削减总用电支出的储能调度计划，以提高最不利可能性下总用电支出1.5%为代价，降低了最不利可能性下用户侧净负荷方差9.7%。相对于完全偏向于削减净负荷方差的储能调度计划，以提高最不利可能性下用户侧净负荷方差4.8%为代价，降低了最不利可能性下总用电支出1.1%。且对于不确定变量在不确定集内所有可能的取值，帕累托前沿所对应的所有储能调度计划都能够保证约束条件是满足的。

图8 经济成本与用户侧净负荷方差的帕累托前沿

2.1节所述方法并不局限于此，以同样方法可以运用ε-约束法优化多个目标，相较于利用加权求和法合成新目标，得以保留各目标独立的物理意义，便于后续分析，免去了对权重选择的讨论。现将常用的用户侧净负荷峰谷差作为一个同样需要考虑的削峰填谷评价目标，以进一步说明2.1节所述方法通过增加SP扩展原算法的实现细节。

3.2 多优化目标的具体模型及其求解

多目标储能调度鲁棒优化流程如图9所示，相较于图3，在算法的Step3部分增加了一个针对用户侧净负荷峰谷差的SP，用于在每次迭代中向MP添加针对新增优化目标的不确定集中最不利的场景。同样的，同时涉及第一阶段决策变量、不确定变量、第二阶段决策变量的不等式约束条件，即使不符合文献[19]规定的形式，也可以转换为ε恒定的优化目标，构成SP加入算法的Step3。

图9 多目标储能调度鲁棒优化流程图

当ε1取值为720、新目标ε2取值为92时，亦即要求所得的储能调度计划实际执行后，对于在图1、图2所示区间内任意波动的光伏出力、用户负荷，都能保证满足各项约束且该日总体用电支出低于720元、用户侧净负荷峰谷差不高于92 kW，并在此基础上尽可能降低净负荷曲线在该日的波动程度。

在这种要求下所得电池储能调度计划的鲁棒最优解如图10所示，与之对应的电池储能系统SOC变化如图11所示。从图中可以发现，为了消纳光伏在午时的发电高峰，达到削减峰谷差的目的，电池储能系统于08:00—09:00进行了放电，为削减峰谷预留容量。

图10 电池储能系统充放电功率(三优化目标，ε1=720、ε2=92)

图11 电池储能系统荷电状态(三优化目标，ε1=720、ε2=92)

对净负荷峰谷差最不利场景的用户侧净负荷如图12所示。新增的SP能够根据当前的储能调度计划，在不确定集中寻找令用户侧净负荷峰谷差最大的场景。在该可能性下，当日总用电支出630元，低于可接受上限的720元；用户侧净负荷峰谷差为92 kW，达到了可接受的上限，是所有可能场景中最大的；储能调度后净负荷方差则为1 250 kW2。由此可见，多个SP能够兼顾多个目标构成的ε-约束，同时涉及第一阶段决策变量、不确定变量、第二阶段决策变量的不等式约束条件即使不符合文献[19]规定的形式，也能用这种方法加以求解。

图12 用户侧净负荷(对净负荷峰谷差最不利的场景)

4 结 论

本文针对含不确定源荷的用户侧削峰填谷储能最优调度问题，研究第一阶段决策取值范围受第二阶段决策限制的鲁棒优化问题及其求解方法，并对传统的列和约束生成算法进行改进，提出用于用户侧削峰填谷的电池储能鲁棒最优调度策略，主要结论如下：

1)对线性约束的单阶段鲁棒优化问题的目标函数为凸函数的情况，应用C&CG算法是一定可行的，但如果约束条件中的不确定集不与决策变量取值范围相独立，那么原C&CG算法就不再适用。对于每个同时涉及不确定集与决策变量的约束条件，可以将其理解为应用ε-约束法后的鲁棒多目标优化问题，由此增加原C&CG算法在一次迭代中的SP数目，只要这些同时涉及不确定集与决策变量的约束条件均为凸函数不等式，那么改进后的算法就是有效的。对两阶段鲁棒优化问题，则需要证明转化为单阶段鲁棒优化问题形式时，最内层函数是凸函数，且同时涉及不确定集与决策变量的约束条件均为凸函数不等式，才能保证应用改进后的算法一定能收敛于鲁棒最优解。

2)在储能调度的鲁棒优化问题中，因对削峰填谷目标最不利的场景与对经济目标最不利的场景相差甚远，需要分别考虑两种场景以取得足够保守的鲁棒最优解时，本文提出的算法能兼顾不确定变量波动对优化目标与复杂约束条件的影响，在源荷波动影响储能出力可行域的情况下，有效求解用于用户侧削峰填谷的电池储能鲁棒最优调度问题。