基于遗传萤火虫算法的液压挖掘机铲斗控制研究

李 捷，王毫旗

(太原科技大学机械工程学院，山西太原 030024)

1 引言

对挖掘机工作装置精确的位置控制是实现挖掘机智能化的基础。本文以某型号小型液压挖掘机为研究对象，通过对液压挖掘机铲斗电液伺服控制系统的研究来实现对铲斗位置的精确控制。文献[1]提出了一种改进的粒子群优化算法，改善了液压挖掘机电液伺服系统的响应特性和铲斗轨迹控制的效果；文献[2]提出一种惯性权重余弦调整的粒子群优化算法用于PID控制参数整定中，使得控制系统响应性能更好；文献[3]提出构建了死区模糊补偿控制系统，通过将传统数字PID控制和变死区补偿模糊控制方法的结合，提高了电液比例系统位置控制的精度。文献[4]提出了一种适应性强的程序，该程序用于提取电液伺服系统的线性化模型，以完成精确的位置控制任务；文献[5]提出了基于两相平衡多目标的智能水滴算法(IWD)和多目标优化方法，提高了对电液伺服系统的控制性能；文献[6]提出了一种基于奇异摄动理论的电液负载转矩跟踪控制方法，运用期望模型补偿的自抗扰控制方法提高系统的高精度和强鲁棒性。文献[7]提出了改进人群搜索算法的优化方法，加快了算法的搜索速度，改善了系统的性能；文献[8]将天牛须搜索算法用于PID控制器的设计，此算法使运算量大大降低，有效缩短了整定时间；文献[9]提出拟混沌人群搜索算法，改善了局部求精能力和全局搜索能力。

为了实现对液压挖掘机铲斗位置的精确控制，在标准遗传算法的基础上对目标函数、选择算子、交叉算子等进行了改进，主要是运用了能够随进化过程自适应改变的非线性交叉概率和变异概率，然后再引入人工萤火虫算法来避免标准遗传算法的早熟现象，最后提出了欧式距离算法停止准则，有效缩短了算法的运算时间。遗传萤火虫算法能够有效避免陷入局部最优的问题，提高了算法的寻优精度并且缩短了算法的收敛时间。通过仿真对比，验证了遗传萤火虫算法的优越性和有效性。

2 液压挖掘机铲斗系统建模

2.1 铲斗电液比例系统原理组成

液压挖掘机铲斗电液比例位置控制系统的结构原理图，其中包括指令元件、控制器、D/A转换器、比例放大器、电液比例阀、液压缸、工作装置、位移传感器等元件，结构原理图如图1所示。

图1 铲斗电液比例位置控制系统结构图

2.2 电液比例阀的传递函数

在实际工作中由于电液比例阀的响应速度比工作装置液压缸的要快，因此把电液比例阀的一阶惯性形式作为传递函数，如下方法

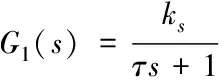
(1)

其中，ks为电液比例阀的流量增益；τ为电液比例阀时间常数。

2.3 电液比例阀控非对称缸传递函数

液压挖掘机工作装置油缸系统结构是非对称液压缸系统，其液压缸的传递函数由电液比例阀滑阀流量线性化方程、液压缸流量连续性方程以及液压缸力平衡方程经过拉普拉斯变换得到[10]，则液压缸活塞杆正向伸出时的传递函数如下方法

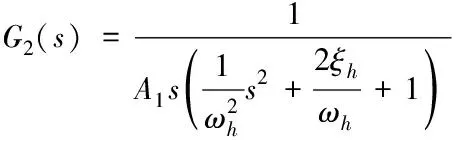
(2)

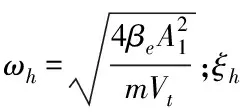
2.4 铲斗电液比例控制系统传递函数

由图1以及式(1)和式(2)可得铲斗电液比例控制系统的传递函数如下方法

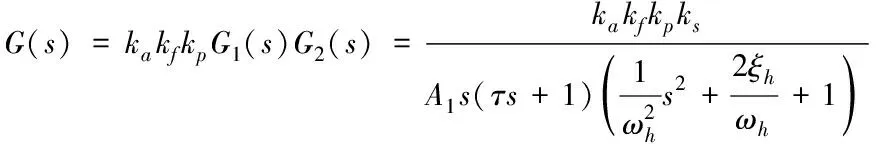
(3)

其中，ka为比例放大器增益；kf为位移传感器增益；kp为PID控制器比例系数。

电液比例控制系统的主要参数如图2所示。

符号值符号值Ka0.5A/VVt2.826×10-3m3Kf10V/mβe800MPaKs2.778×10-4m3/s·Akce5.508×10-12A15.675×10-3m2ωh337.6rad/sτ0.05ξh0.01

代入图2中的参数可得铲斗电液比例控制系统的传递函数如下方法

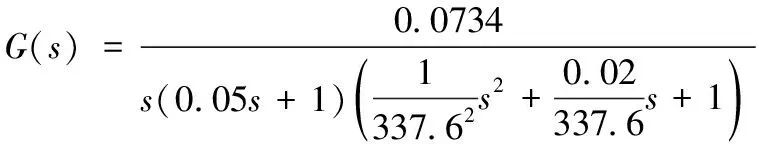
(4)

3 遗传萤火虫算法

3.1 改进的遗传算法

3.1.1 基因编码及构造初始种群

对参数kp、ki、kd采用二进制编码形式进行编码。用长度为10的二进制码表示，编码后生成的染色体如下方法

[kp1，…，kp10，ki1…ki10，kd1，…，kd10]

(5)

根据工程方法确定每个参数的取值范围，然后在范围之内生成初始种群如下方法

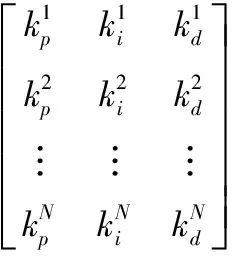
(6)

3.1.2 适应度函数的改进

在ITAE的基础上对系统评价指标进行改进，将改进后的评价指标作为系统的适应度目标函数，目标函数如下方法

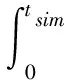
+αOs+βSSe+γts+δtr

(7)

其中，tsim为系统仿真时间；w1，w2为权重；e(t)为系统误差；u(t)为控制器输出；α，β，γ，δ为系统性能参数权重；Os为超调量；SSe为稳态误差，ts为调节时间，tr为上升时间。适应度函数取目标函数的倒数如下方法

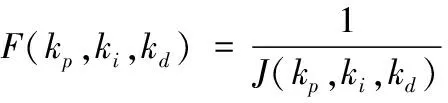
(8)

3.1.3 选择算子的改进

先按式(7)(8)计算每个个体的适应度值，接着将个体按照其适应度值的大小降序排列，并且将排序之后的个体平均分成五份。将适应度值较高的前五分之一个体按照精英保留策略复制至下一代作为父代亲本；然后将适应度值较差的后五分之一个体直接淘汰；最后将中间剩余的五分之三个体按照式(9)—(11)进行选择。

Pi=Q(1-q)i-1

(9)

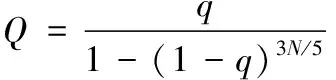
(10)

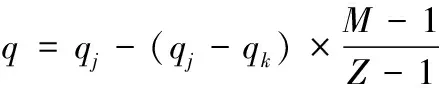
(11)

其中，Pi为第i个个体被选择的概率；Q为个体的选择概率；i为中间3/5种群中个体的排列序号；q为最佳个体的选择概率。因为最佳个体的选择概率会随着迭代次数的变化而发生改变，故提出q值的计算公式如下方法

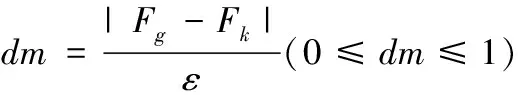
(12)

其中，qj为M代最佳个体选择概率；qk为M代最差个体选择概率；Z为最大迭代次数。

3.1.4 交叉算子的改进

遗传算法中适合二进制编码的交叉操作有多种形式：单点交叉、两点交叉、多点交叉以及均匀交叉等。基于算法的可操作性考虑，这里主要运用单点交叉和两点交叉两种形式。引入个体的相似度dm，表示种群中两个体的相似程度。则个体g和k的相似度公式如下方法：

其中，ε为种群中个体适应度最大值与最小值之差，0<ε；Fg为种群中个体g的适应度值；Fh为种群中个体h的适应度值。若0.5≤dm≤1，说明两个体之间相似程度较低，则使用单点交叉操作；若0≤dm<0.5，说明两个体相似程度较高，则使用两点交叉操作。

3.1.5 变异算子

运用均匀变异算子进行单点变异操作，变异时，在染色体上随机选择一个二进制码位进行变异，然后形成新的染色体个体。

3.1.6 交叉概率和变异概率的改进

提出一种新的自适应调整交叉概率和变异概率，自适应调整交叉概率和变异概率的公式如下方法：

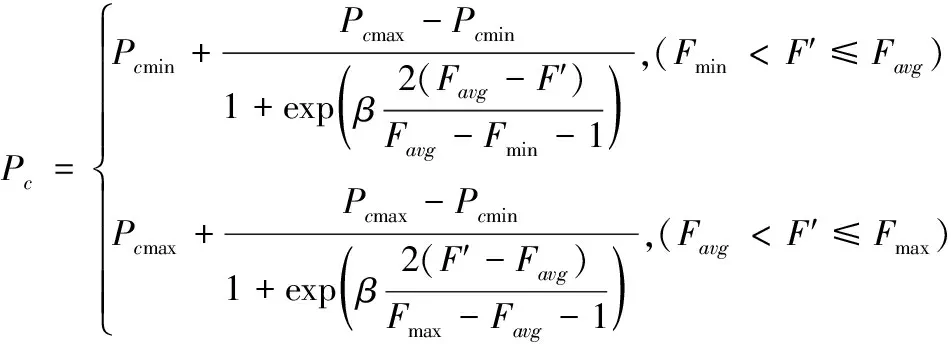
(13)

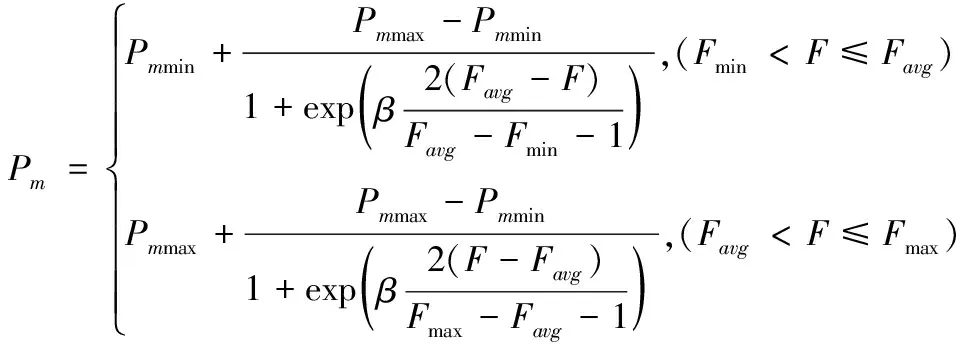
(14)

其中，Pcmax、Pcmin为交叉率的最大值与最小值；β为曲线平滑因子，β=9.9034；Favg为当前种群个体适应度的平均值；Fmax、Fmin为当前种群个体适应度的最大值与最小值；F′为交叉两个体的较大的适应度值；Pmmax、Pmmin为变异率的最大值与最小值；F为当前个体适应度值。

3.2 人工萤火虫优化算法

萤火虫算法顾名思义就是通过观察萤火虫群体的行为和群体间的交流而提出的一种群智能算法，由剑桥大学的Xin-She Yang教授提出。K.N.Krishnanad和D.Ghose提出了人工萤火虫群优化算法，该算法是一种新型的群智能优化算法[11-13]。提出将遗传算法选择操作中直接保留的精英个体和经过交叉、变异的个体共同组成较优种群Ⅰ，将人工萤火虫群优化算法作用于较优种群Ⅰ，能够提高算法的寻优精度和收敛速度，避免陷入局部最优。具体操作如下：

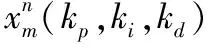
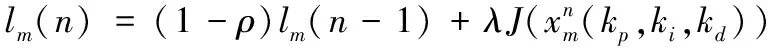
(15)

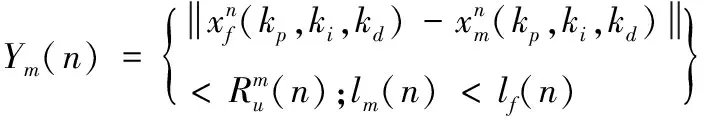
(16)

3)按照式(17)计算萤火虫m向荧光素值比自己高的萤火虫f移动的概率pmf(n)，并按式(18)更新萤火虫m移动后的位置如下方法

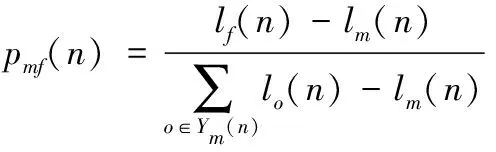
(17)

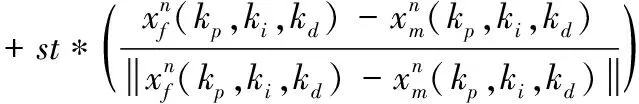
(18)

4)根据式(19)更新动态决策域的半径如下方法

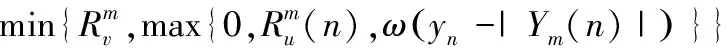
(19)

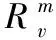
3.3 确定算法停止准则

提出一种停止准则，即欧式距离停止准则。欧式距离停止准则是以每代最优的PID参数构成的三维决定向量V[kpkikd]T为依据，计算第k代的决定向量Vk与第k+1代的决定向量Vk+1之间的欧式距离。通过计算连续多代相邻决定向量之间的欧氏距离是否小于某一设定值，若小于该设定值则说明达到终止条件，即终止程序。本文采用欧式距离停止准则与最大进化次数共同作为遗传萤火虫算法的停止准则，即双重停止准则，可以有效减少算法的运算时间。

4 遗传萤火虫算法的PID参数整定

4.1 经典PID控制器

经典的PID控制器，控制原理比较简单，适应性较强，是一种典型的线性控制器。其控制规律满足如下方法

(20)

其中，e(t)为偏差信号；u(t)为控制器输出值；kp为比例系数；ki为积分系数；kd为微分系数。通过遗传萤火虫算法对PID控制器的参数进行优化，其控制框图如图3所示。

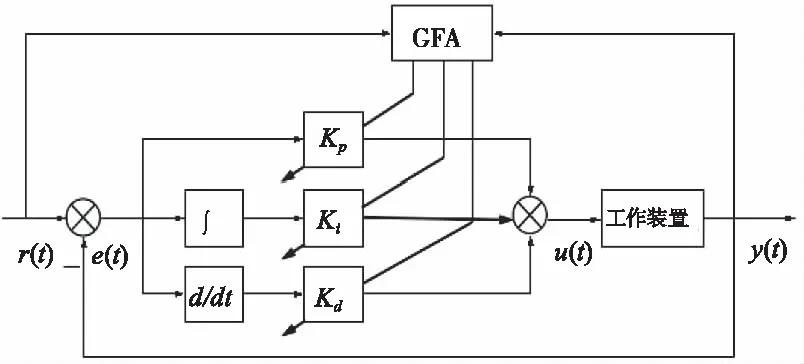
图3 遗传萤火虫算法优化PID参数示意图

4.2 遗传萤火虫算法整定PID参数的具体实现步骤

其步骤可总结如下：

1)根据工程方法确定PID控制器各参数的范围，kp∈[0，100]，ki∈[0，1]，kd∈[0，1]，采用二进制编码方法对PID控制器的三个参数进行编码，种群规模N设为30，然后随机产生初始种群；

3)计算是否满足停止准则，若满足停止条件(达到最大迭代次数100或欧式距离小于设定值)则输出最优解，终止程序，若不满足停止条件则进行下一步操作；

4)按照式(9)—(11)改进的选择算子对个体进行复制选择，然后结合改进的交叉算子以及自适应非线性调整概率公式进行交叉和变异操作，然后产生较优种群Ⅰ；

5)引入人工萤火虫算法对较优种群Ⅰ再进行遗传进化，然后生成较优种群Ⅱ，最后合并种群Ⅰ和种群Ⅱ为新的种群进入下一次迭代过程，并返回步骤2)计算个体的适应度值，再根据步骤3)计算是否满足停止准则，若满足此准则，终止程序，否则继续按照上述步骤进行操作。遗传萤火虫算法整定PID参数流程图如图4所示。

图4 遗传萤火虫算法流程图

5 仿真设计与结果分析

5.1 确定实验参数

将标准遗传算法和遗传萤火虫算法的种群规模均设为30，最大进化次数均设为100。标准遗传算的交叉概率与变异概率均为固定值，设为Pc=0.8，Pm=0.01。遗传萤火虫算法中设Pcmax=0.8，Pcmin=0.3；Pmmax=0.075，Pmmin=0.01。式(10)中取w1=0.999、w2=0.001、α=1.5、β=15、γ=7、δ=1。人工萤火虫算法中ρ=0.4；λ=0.6；st=0.03；ω=0.08；yn=6。

5.2 仿真设计

运用MATLAB/Simulink模块来进行仿真设计将标准PID控制与运用标准遗传算法和遗传萤火虫算法的控制进行对比实验。进一步，在Matlab/Robotic Toolbox中完成挖掘机器人挖掘基坑的轨迹规划，为了达到良好的控制效果，采用挖掘机器人关节空间分段多项式插值法来进行挖掘基坑的轨迹规划，将挖掘的过程分为5段轨迹。将规划后的数据结果即铲斗关节角度值作为期望目标值输入到控制器中，观察在各种算法整定下对期望目标值的跟踪效果。进一步验证各种算法的整定效果。

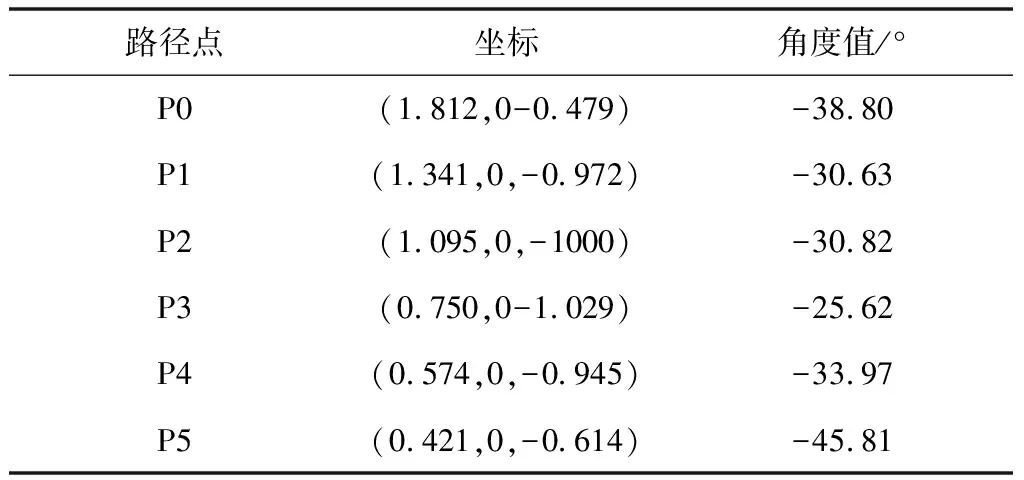
路径点坐标角度值/°P0(1.812,0-0.479)-38.80P1(1.341,0,-0.972)-30.63P2(1.095,0,-1000)-30.82P3(0.750,0-1.029)-25.62P4(0.574,0,-0.945)-33.97P5(0.421,0,-0.614)-45.81

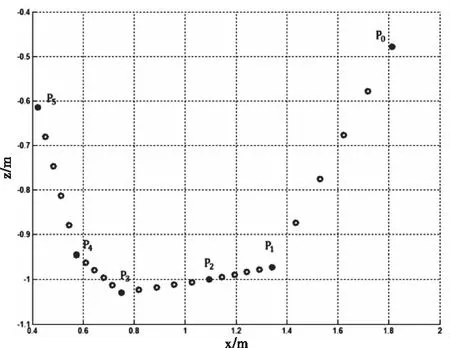
图6 挖掘机器人基坑挖掘轨迹图

5.3 仿真结果分析

三种不同算法整定下系统的单位阶跃响应如图8所示。经过三种不同算法整定后的PID参数和适应度最优值如图7所示。从图8可以得出：三种不同整定算法曲线的变化趋势基本相同，均没有超调现象出现，标准PID算法整定后系统的响应速度较慢，调节时间较长，系统的控制效果差。标准遗传算法和遗传萤火虫算法整定后的系统，在调节时间和响应速度方面都都得到了较大的提高。经过遗传萤火虫算法整定后的系统响应速度最快，上升时间和调节时间也都最小。表明遗传萤火虫算法可以更有效的对PID参数进行整定，提高系统的控制精度。

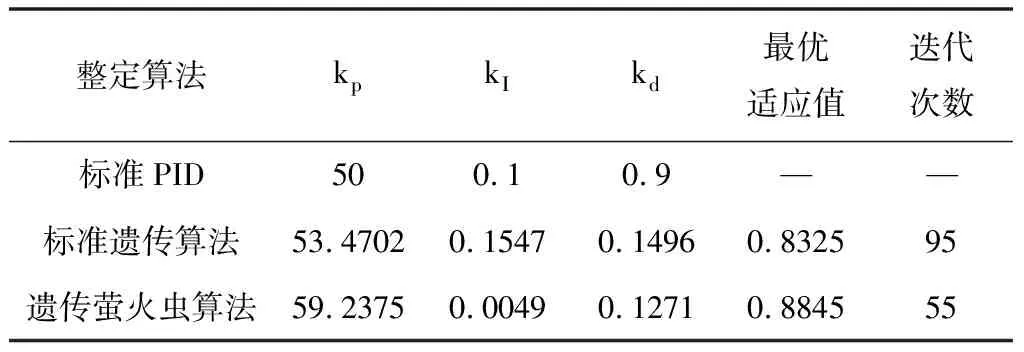
整定算法kpkIkd最优适应值迭代次数标准PID500.10.9——标准遗传算法53.47020.15470.14960.832595遗传萤火虫算法59.23750.00490.12710.884555

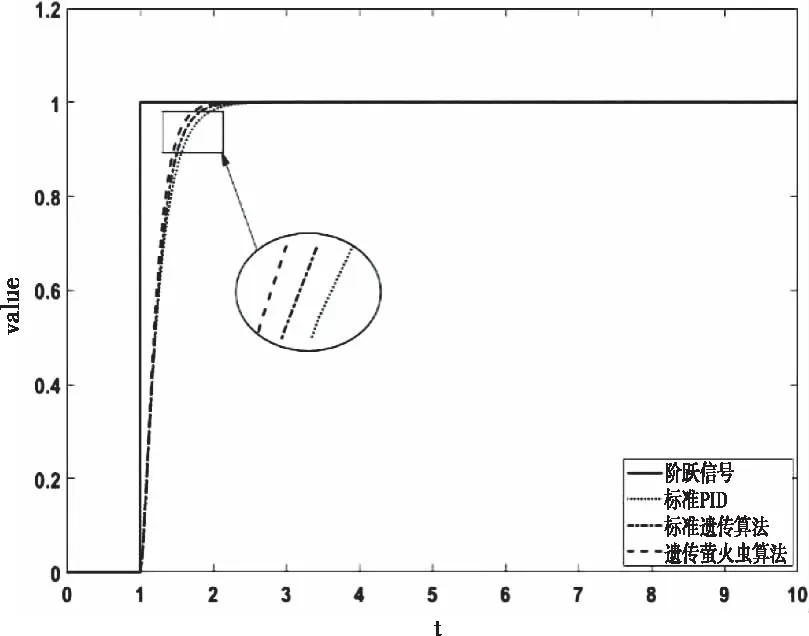
图8 三种算法的阶跃响应对比图

三种不同算法整定下系统的正弦响应如图9所示。从图9可以得出：三种整定算法的响应跟踪曲线都有迟滞现象，其中遗传萤火虫算法整定方法的跟踪误差最小，发生迟滞的时间也最短，表现出了较优的动态特性。

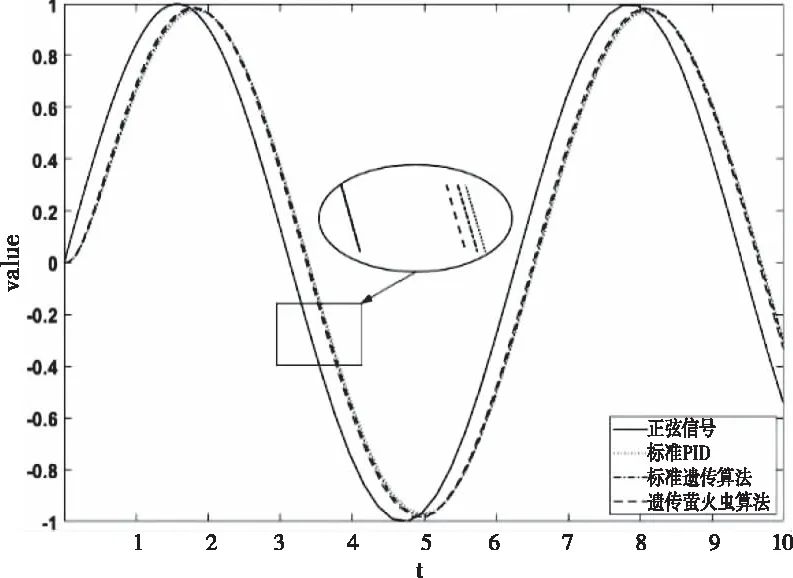
图9 三种算法的正弦响应对比图

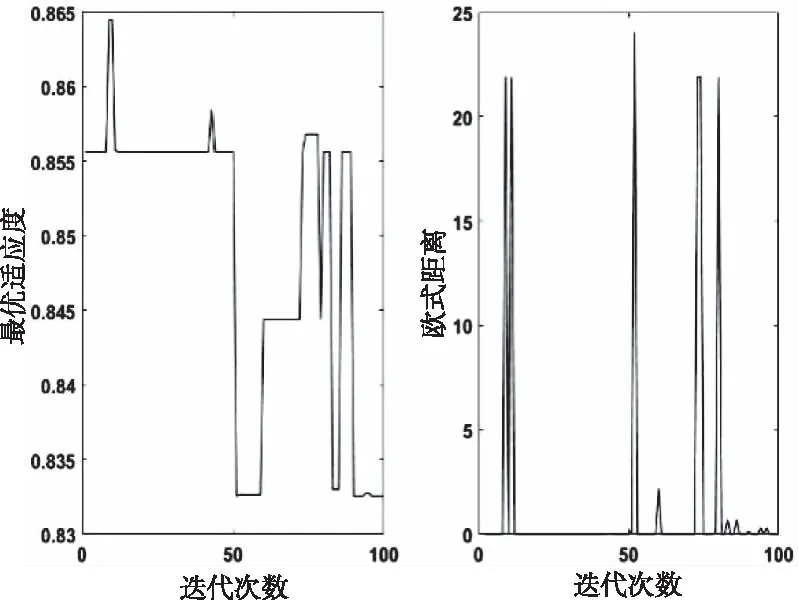
图10 标准遗传算法最优适应度和欧氏距离随迭代次数变化曲线图

标准遗传算法和遗传萤火虫算法整定下最优适应度和欧式距离随迭代次数变化曲线如图10和图11所示。从图10和图11可得出：标准遗传算法的最优适应度是随着迭代次数的增加而减小的，且收敛速度较慢，直到进化到第95代才获得最优适应度，欧氏距离也在快达到最大迭代次数时才逐渐减小为0。遗传萤火虫算法的最优适应度是随着迭代过程的进行而持续增加的，在进化到第55代就达到了最优，且欧氏距离也在第55代开始就恒等于0，提前满足了算法停止准则，有效的缩短了算法的运算时间，表明遗传萤火虫算法大大提高了收敛速度和寻优精度。

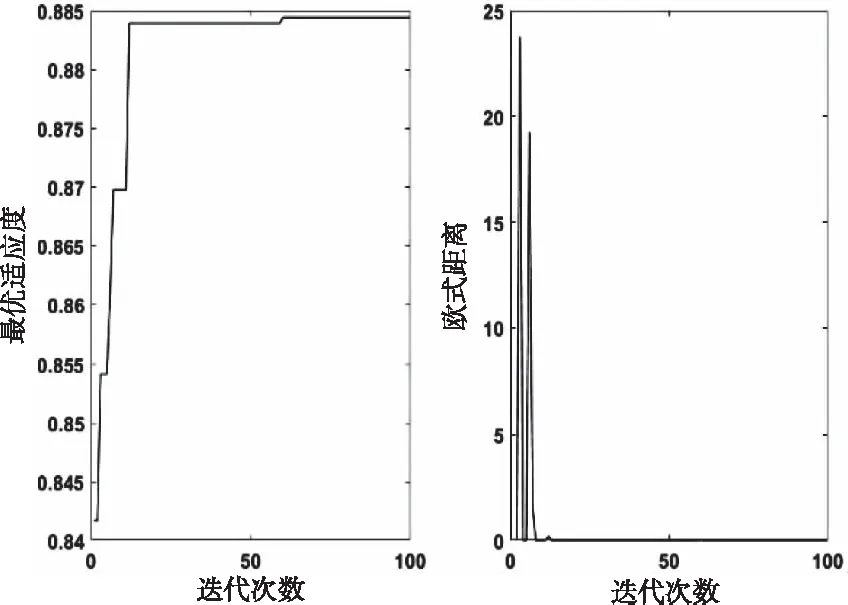
图11 遗传萤火虫算法最优适应度和欧氏距离随迭代次数变化曲线图

标准遗传算法和遗传萤火虫算法整定过程中PID参数的变化曲线如图12和图13所示，能够看到PID参数在遗传萤火虫算法整定过程中变化不大，且能够较早的达到全局最优值，表明遗传萤火虫算法具有较强的参数寻优能力，还有效的解决了标准遗传算法在整定过程中参数容易陷入局部最优的问题。

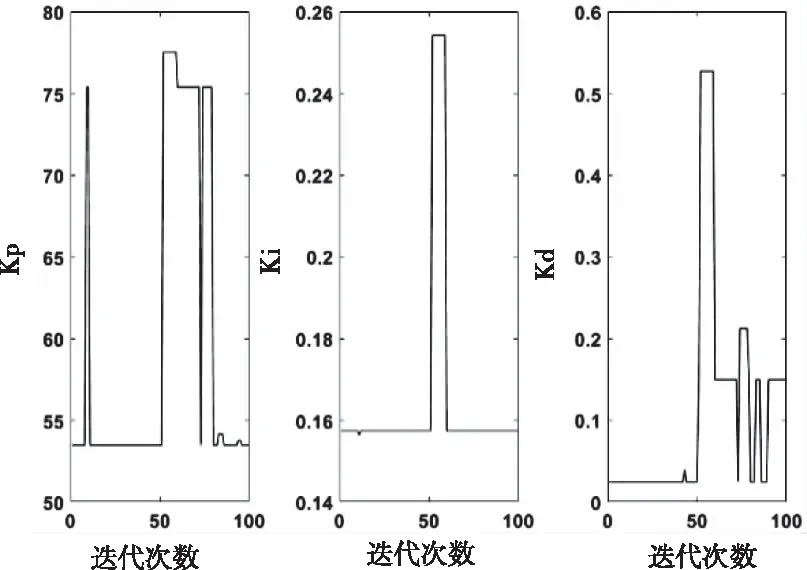
图12 标准遗传算法整定PID参数变化曲线图

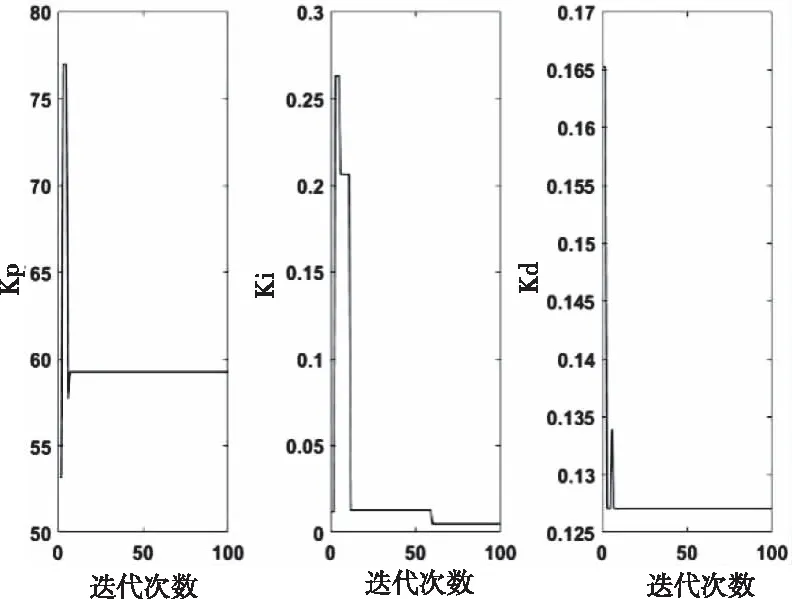
图13 遗传萤火虫算法整定PID参数变化曲线图

三种不同算法整定下控制系统对规划的目标铲斗关节轨迹跟踪曲线如图14所示。实际上由于从控制器发出指令信号到铲斗关节开始运动，这之间会存在延迟，所以图中跟踪曲线不能在一开始就对目标轨迹进行跟踪。从图1中可以看出，使用标准遗传算法和遗传萤火虫算法可以有效减小对目标铲斗关节轨迹的跟踪误差，其中遗传萤火虫算法作用明显，跟踪响应速度最快，与目标轨迹的跟踪误差最小。表明了遗传萤火虫算法在铲斗关节轨迹跟踪方面的良好性能，同时也说明遗传萤火虫算法在挖掘机铲斗位置控制方面的有效性。

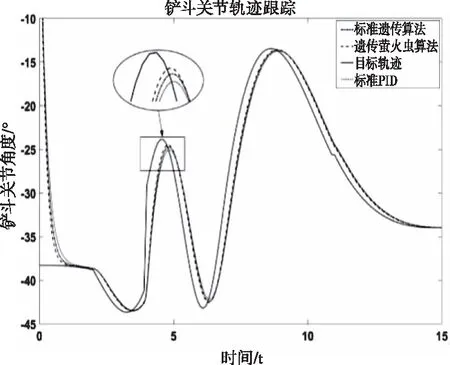
图14 铲斗关节轨迹跟踪曲线图

6 结论

提出一种遗传萤火虫算法用于挖掘机电液伺服控制系统PID控制器参数的整定。在标准遗传算法的基础上设计了改进的交叉算子和自适应调整的非线性交叉概率和变异概率；将人工萤火虫算法引入遗传算法中；并提出遗传萤火虫算法欧氏距离停止准则。仿真结果表明，遗传萤火虫算法能够有效提高控制系统的响应速度和动态特性，大大提高了算法的收敛速度和寻优精度，并且解决了容易陷入局部最优的问题，强化了算法的全局寻优能力，系统的鲁棒性也更好。从设计的挖掘机器人铲斗关节轨迹跟踪仿真可知，遗传萤火虫算法在铲斗关节轨迹跟踪方面有着良好的性能，表明遗传萤火虫算法在挖掘机铲斗位置控制方面的有效性，这对于研究液压挖掘机智能化挖掘有一定的理论指导意义。