准Z源光伏逆变直流链电压积分滑模控制仿真

胡润滋，古济铭，赵 科，何立婧

(1. 国网重庆市电力公司电力调度控制中心，重庆 400014；2. 重庆大学输配电装备及系统安全与新技术国家重点实验室，重庆 400044)

1 引言

由于光伏输出直流电压的变化范围较大，而准Z源逆变器(quasi-Z-source inverter，qZSI)具有可以升降压，输出电压调节范围大、输出波形畸变小以及允许逆变桥短路或开路等特点，因此被广泛应用到光伏系统中。

滑模控制作为一种非线性控制方法，具有良好的鲁棒性和自适应性，在电力电子变换器的控制中得到了广泛的研究。文献[8]提出了一种单相Z源网络的电压纹波前馈控制策略，调制系数通过电压纹波前馈控制进行校正，为了解决重载条件下直流母线输出电压波动范围较大的问题，所提出的控制策略明显削弱了直流链电压纹波对交流侧波形的不良影响，但当电源输出电压变化范围较大时，系统响应速度较慢。文献[9]提出了一种Z源网络直流链电压直接控制策略，设计了一种经典PID补偿器，但由于增加了方波检测电路，增加了系统的成本，在实际应用中较多采用间接控制。文献[10]采用电感电流和电容电压作为状态变量，对Z源直流链电压进行滑模控制，但没有对电流进行积分，输出响应较慢，电压超调较大。

本文提出了一种应用于准Z源网络的带电流积分滑模控制方法，准Z源固有的右半平面零点的存在使控制器的设计变得复杂，同时限制了电压模式控制器补偿网络的带宽。采用的状态变量为电感电流误差、电容电压误差以及它们误差的积分，使变换器动态响应快，电压超调相对较小，跟踪参考信号性能好，选择间接控制方法来控制直流链的电压值。测试了在负载扰动下的鲁棒性，通过Simulink仿真表明，在光伏板输出随负载非线性变化条件下，所设计的滑模控制器能够更好的跟踪参考信号，具有鲁棒性强，保证系统稳定的特点。

2 准Z源逆变器的基本原理

传统的逆变电路可分为电压型和电流型逆变电路。准源逆变器的系统结构如图1。电感、和电容、构成源网络，逆变桥式电路由6只开关管～组成。插入直通时间来控制逆变电路的升降压，可使>实现升压。根据电感伏秒平衡可得

直流输入电压和直流链电压的关系为

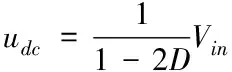
(1)

直流输入电压和电容电压的关系为

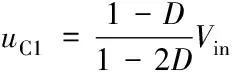
(2)

直流输入电压和电容电压的关系为

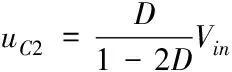
(3)

其中表示直流输入电压，表示直流链电压，表示电容电压，表示直通占空比，在0<<05的条件下，逆变器就能实现升压。

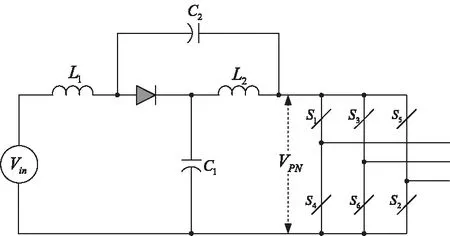
图1 三相准Z源逆变器拓扑

3 准Z源的数学模型

3.1 大信号模型

令==，==。

1)直通状态

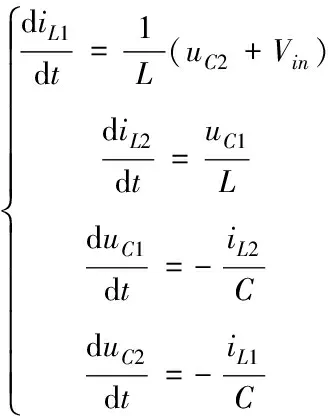
2)非直通状态

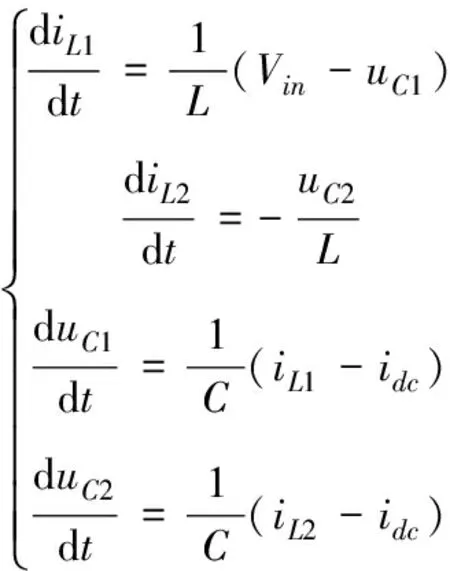
3.2 状态空间模型

(4)

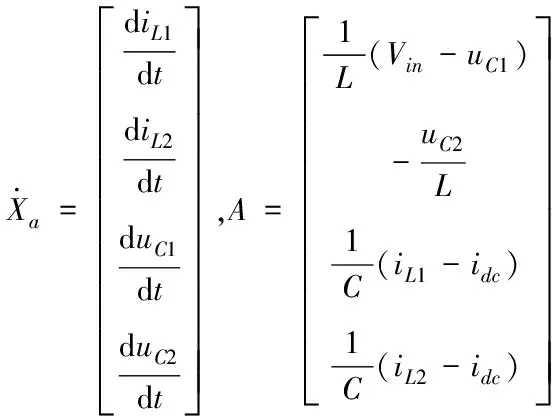
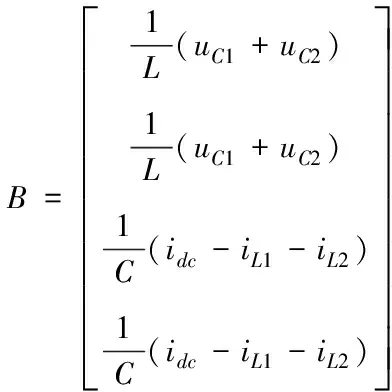
其中

4 电流滑模控制器的设计

假定准Z源逆变器(qZSI)工作在连续电流模式(CCM)，下面详细介绍滑模控制器的设计过程。

4.1 滑模面设计

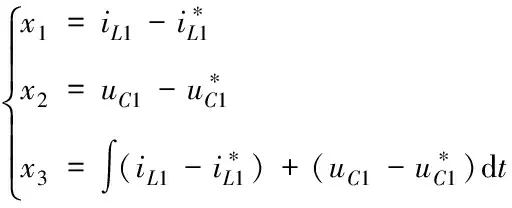
(5)

选择滑模面

=++=

(6)

则

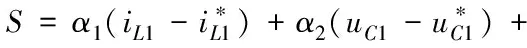
4.2 推导等效控制律

对求导得

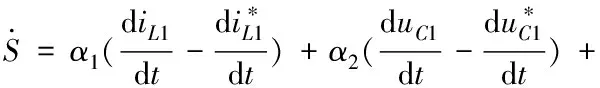
(7)

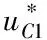
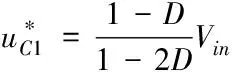
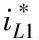
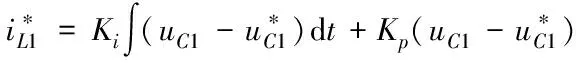
(8)

其中，为积分系数，为比例系数。

把式(8)代入式(7)得

(9)

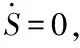
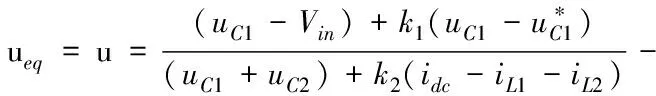
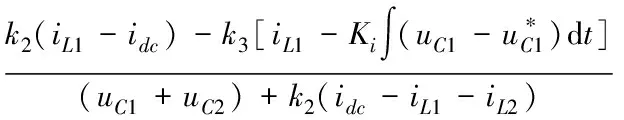
(10)

其中:=+(-1)；=(-)；=。

图2所示为的整体控制框图，等效控制律是一个连续量，与直通占空比等效，值域为[0，05)。

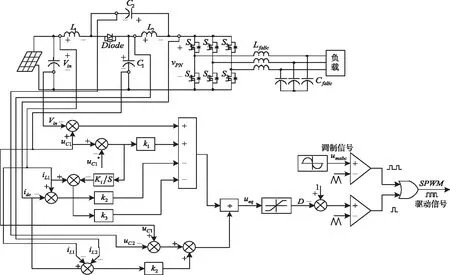
图2 qZSI整体控制框图

4.3 存在条件

根据滑模控制理论，所设计的直流链电压带电流积分滑模控制器应在系统所有输入和负载条件下均满足到达、存在和稳定性3个条件。

控制器采用的控制律

当<0，=1时，由源变换器的原理可知，直通占空比≤05，结合式(2)，此时1→∞，通过(6)定义可使滑模面满足到达条件。

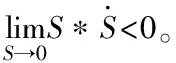
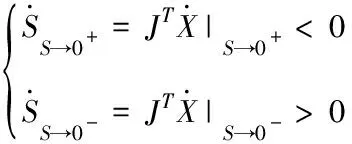
上式可分为两种情况

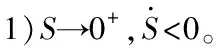
用u=0替换u→0，代入式(9)得

(11)

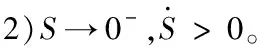
用u=1替换u→0，代入式(9)得

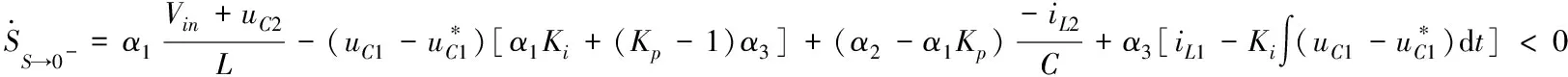
(12)

其中，和为已知参数；、1和2的值在一定范围内波动，因此，有必要考虑其值的临界点。如果最大或最小工作状态满足存在条件，则整个工作状态满足存在条件。1、2和都为瞬时状态变量，设计过程较复杂，把状态变量1、2和用期望设计的稳态值代替，为1()、2()和()。此方法能够让系统在小范围内满足存在条件。即存在条件如下式

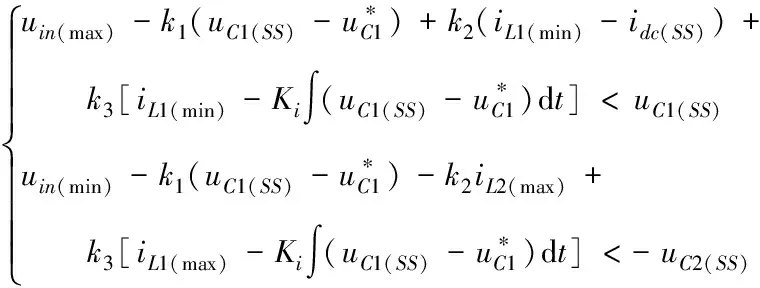
(13)

4.4 稳定条件

首先推导系统的理想滑模动态，随后进行平衡点分析，最后推导维持稳定的条件。

1)理想滑动动态

对于模式的系统，用u代替式(4)中的u，将不连续系统转换为理想滑模连续系统，即

(14)

将等效控制信号u的表达式(10)代入上式得

(15)

上式表示带电流积分滑模控制的理想滑动动态。

2)平衡点分析

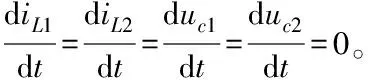
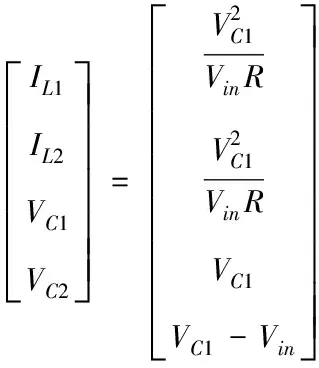
(16)

3)理想滑动动态的线性化

将理想滑动动态在平衡点附近线性化

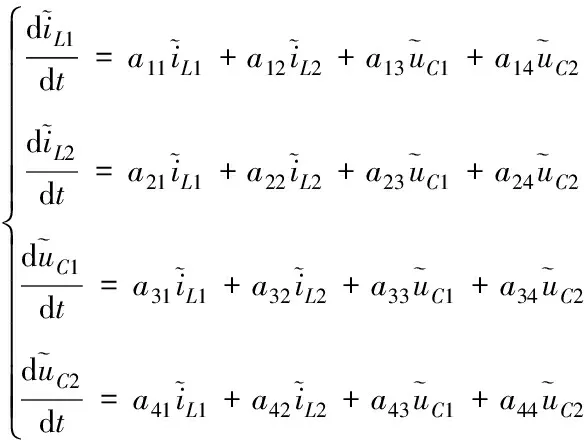
(17)

上式为式(15)的交流项，令

线性化系统化的特征方程为

|-|=0

(18)

其中，为特征系数矩阵，为单位矩阵。式(18)确定了系统的动态特性和稳定性，如果的全部极点在左半平面，那么系统在所设计的闭环系统滑模面上稳定运行。由式(13)和式(18)来选择满足稳定运行的滑模系数。

5 仿真和实验结果

5.1 光伏电池的建模

工程中光伏组件的工作特性主要采用单二级管等效电路来描述，如图2。

图3 光伏组件的单二极管等效电路

由图3可以写出光伏组件的数学表达式。

=--

(19)

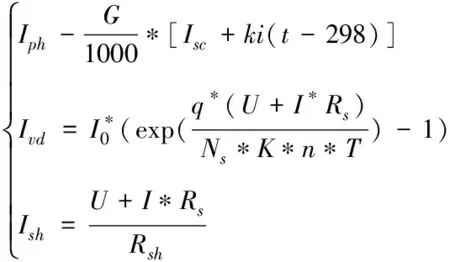
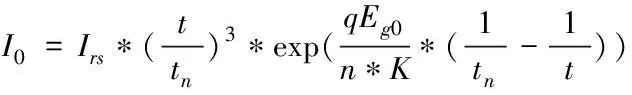
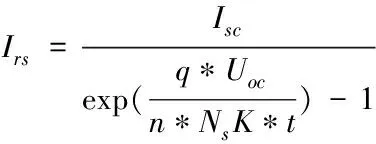
光伏组件的数学模型可以由以上表达式描述，其中参数的含义见表1。

表1 参数的物理意义及取值

参数设定值见表2。

表2 参数设置

根据上述公式在中搭建仿真模型，如图4。

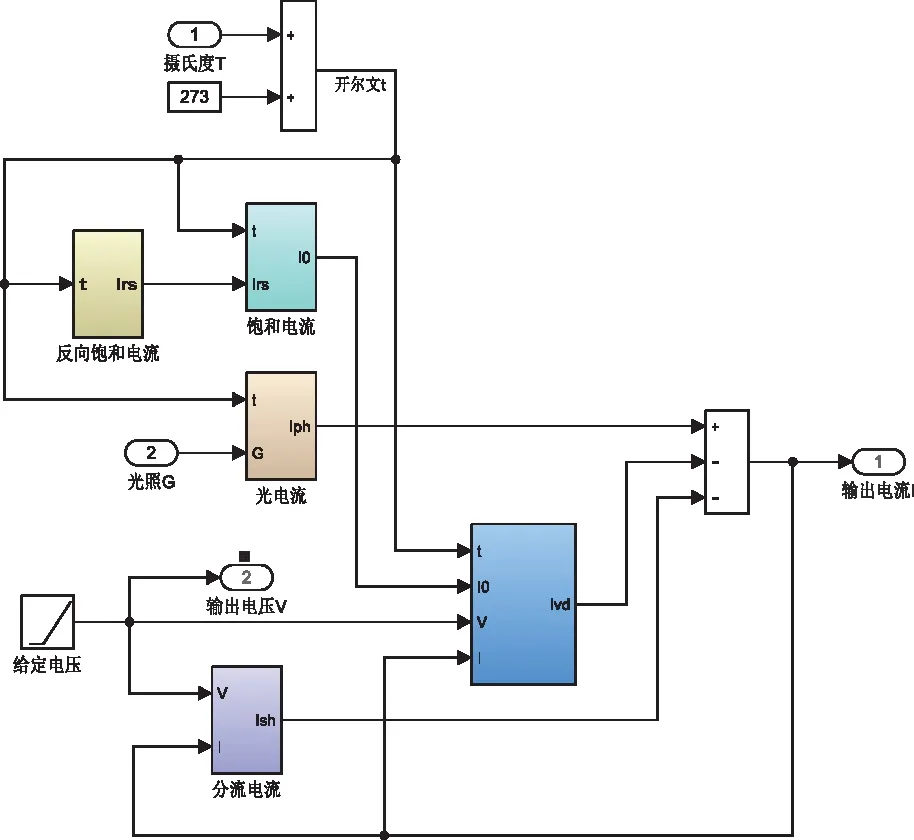
图4 光伏组件的数学模型

光照强度为=1000的工作条件下，温度在=25℃，=50℃，=75℃变化，仿真得到光伏电池的和曲线结果如图4()，()所示。温度为=25℃的工作条件下，光照强度在=600，=800，=1000变化，仿真得到光伏电池的和曲线结果如图5()，()。

图5 光伏电池的VI和PV曲线

5.2 准Z源网络参数的选择

准源网络的参数设计过程在文献[14]中进行了详细的介绍。准源网络工作在连续导电模式()。

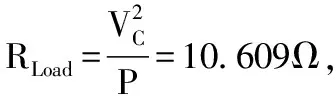
5.3 仿真结果

把设计的准源参数代入仿真模型中。在仿真中，用中光伏阵列模块代替光伏电池。直流链电压在滑模控制下的仿真电路图如图6。

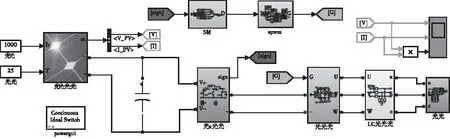
图6 仿真电路图

在负载扰动下，05时负载由=10609变成=5345。直流链电压出现暂态过程，经过3左右的时间恢复了稳态值。直流链电压峰值V、电容电压V波形分别如图7()和图8()。

在无积分的传统滑模控制器作用下，05时负载由RLoad=10.609Ω变成R=5.345Ω。直流链电压峰值V、电容电压V波形分别如图7()和图8()。

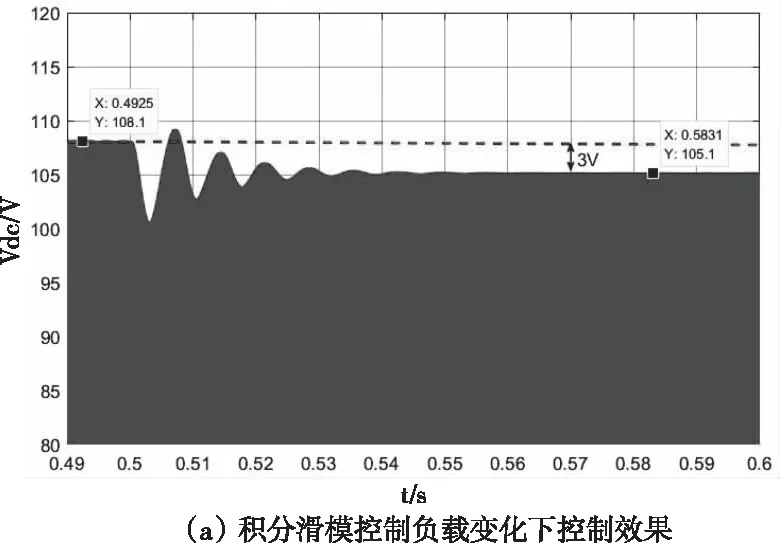
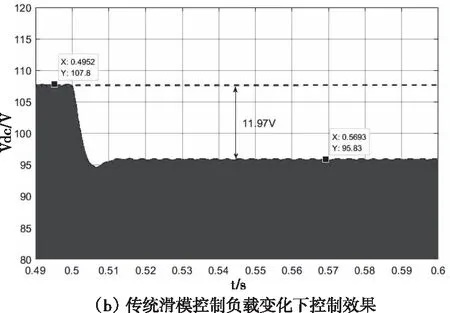
图7 直流链电压波形图

可知，带电流的积分滑模控制器仿真结果波形更好，能更好的跟踪参考信号，表明滑模控制器设计的合理性。

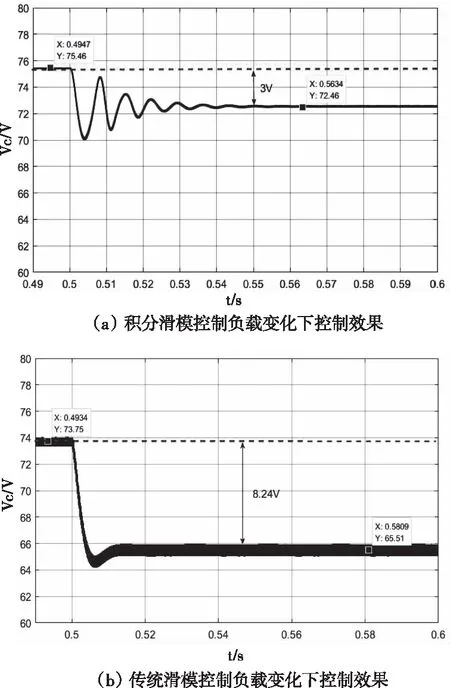
图8 电容电压波形图

逆变器输出侧的相电压波形图如图9，经过滤波后的单相电压波形图如图10。其中带积分滑模控制负载扰动如图()，无积分滑模控制负载扰动如图()。

图9 逆变后ab相波形图

图10 滤波后abc三相波形图

6 结论