改进的UKF乒乓球轨迹预测算法
尹 朵,丁文龙,邱 崧
(华东师范大学 通信与电子工程学院,上海 200241)
0 引 言
近年来,机器视觉技术在国内外获得快速发展。在机器视觉研究中,实现对目标物体的识别与跟踪具有重要意义。单纯的目标检测跟踪并不能准确预判下一时刻物体的运动状态和位置,物体的轨迹预测逐渐成为机器视觉领域的重点和难点。
目前常用的轨迹预测方法主要包括:基于传统多项式拟合的动态轨迹预测、基于卡尔曼滤波的动态轨迹预测、基于神经网络的动态轨迹预测。其中,基于传统多项式拟合的动态轨迹预测通过拟合含有1个参数的阶多项式,在原始数据足够多的情况下,逼近函数曲线,使得误差最小化,得到运动物体轨迹预测的函数曲线,该原理简单、易于实现、建模迅速,适用于小数据量、简单的轨迹预测,缺点是精度不高,拟合阶数越高、系统越发散;基于卡尔曼滤波的动态轨迹预测通过前一时刻的估计值和当前时刻的观测值更新对状态变量的估计,实现对下一时刻的轨迹位置的预测,该方法对运动状态频繁改变的运动目标具有很好的适应性,但无法长时间进行轨迹预测;基于神经网络的动态轨迹预测可以有效地学习运动目标的历史运动状态,利用机器学习方法建立输入输出的映射关系,有效实现运动目标的轨迹预测,该方法可以充分逼近非线性系统,轨迹预测结果精确,但需要依赖大量数据训练模型,实时性差。
近年来,对乒乓球轨迹预测的研究主要是围绕无旋球展开,对旋转球的研究更多地集中在旋转球识别分类上,或采用机器学习的方式进行旋转球的轨迹预测。文献[1]基于4台高速1394火线相机和一台功能强大的工业PC构成的高速视觉系统,提出了一种取决于摩擦系数和垂直恢复系数的旋转速度的新型物理弹跳模型,用于球轨迹预测。文献[2]构建了一个集成的视觉系统来观测乒乓球的旋转运动,并利用位置和自旋信息,通过扩展卡尔曼滤波器(EKF)来实现轨迹预测。文献[3]提出了一种通过反向传播神经网络(BPN)进行轨迹预测的方案,通过2个神经网络分别对碰撞前后的飞行抛物线进行学习训练,通过第一抛物线的10个点即可预测轨迹。文献[4]通过构建空气动力学模型以及回弹模型对乒乓球轨迹进行预测,并根据预测的轨迹计算击球点球的状态。
上述方法在一定程度上提高了轨迹预测的精度,但存在硬件要求高、算法复杂、忽略旋转球角速度等问题。本文提出了一种双目视觉下基于无迹卡尔曼滤波及运动学模型的轨迹预测算法,首先通过无迹卡尔曼滤波的方式对碰撞前轨迹进行预测;预测到落点后,采用碰撞模型及运动学模型预测碰撞后轨迹。该方法能够更加准确地实现乒乓球的轨迹预测,且对视觉系统硬件性能要求较低。经实验验证,该方法对碰撞后乒乓球轨迹预测实时性更高,预测较准确。
1 改进的基于UKF的乒乓球轨迹预测算法
乒乓球轨迹的预测是指通过乒乓球的部分三维世界坐标预测乒乓球的轨迹,从而确定乒乓球的落点。对乒乓轨迹预测的要求主要分为实时性及准确性两部分。采用传统多项式拟合方法预测乒乓球轨迹的方法实时性较好,但对于旋转乒乓球的预测效果较差;基于神经网络的轨迹预测方法可以对旋转乒乓球轨迹进行有效预测,但需要大量数据训练模型。本文采用无迹卡尔曼滤波及运动学模型对旋转乒乓球轨迹进行预测,可以兼顾实时性的同时保证旋转球预测的准确性。
1.1 基于UKF的乒乓球碰撞前轨迹预测
乒乓球在运动过程中,由于在击球瞬间球拍对乒乓球作用力、即马格努斯力的方向不一定完全通过球心,乒乓球在飞行过程中会产生旋转。旋转的乒乓球存在自身角速度,如果直接将其视为质点而忽略角速度,在轨迹预测的结果中会出现较大误差。飞行过程中,旋转的乒乓球主要会受到重力、空气阻力和马格努斯力三个力的作用,影响马格努斯力的主要因素就是角速度,若使用硬件设备直接获取角速度需要配备超高速摄像机或红外设备,成本昂贵,实验条件难以保证。本文采用UKF间接估计角速度这一未知状态。
UKF是一种基于最小方差估计准则的非线性高斯状态估计器,采用无损变换(Unscented Transform,UT)来近似系统状态的后验均值及后验协方差,所需估计时间更短,精确度更高。
离散非线性系统可以用一个过程方程和一个观测方程表示,其数学表述可写为:
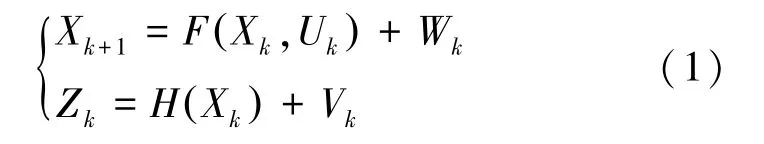
其中,为状态过程函数;为观测过程函数;U为时刻输入向量;Z为时刻观测向量;W和V分别为时刻过程噪声和量测噪声,两者互不相关且均为高斯白噪声;X为时刻运动状态向量。
1.1.1 系统过程方程构建
对于旋转的乒乓球,过程方程是非线性的,而观测方程是线性的。采用9维向量表示乒乓球的状态变量,具体公式如下:

其中,p,p,p表示乒乓球在,,轴的坐标;v,v,v分别表示乒乓球在,,轴的速度;ω,ω,ω分别表示乒乓球在,,轴的角速度。
观测向量用三维向量表示,即通过双目视觉得到的乒乓球三维坐标信息,见式(3):
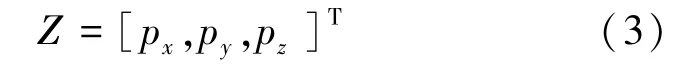
定义 [p,p,p,v,v,v,ω,ω,ω]为系统时刻的9维状态向量,构建乒乓球运动模型的系统过程方程,列出的方程分别如下:
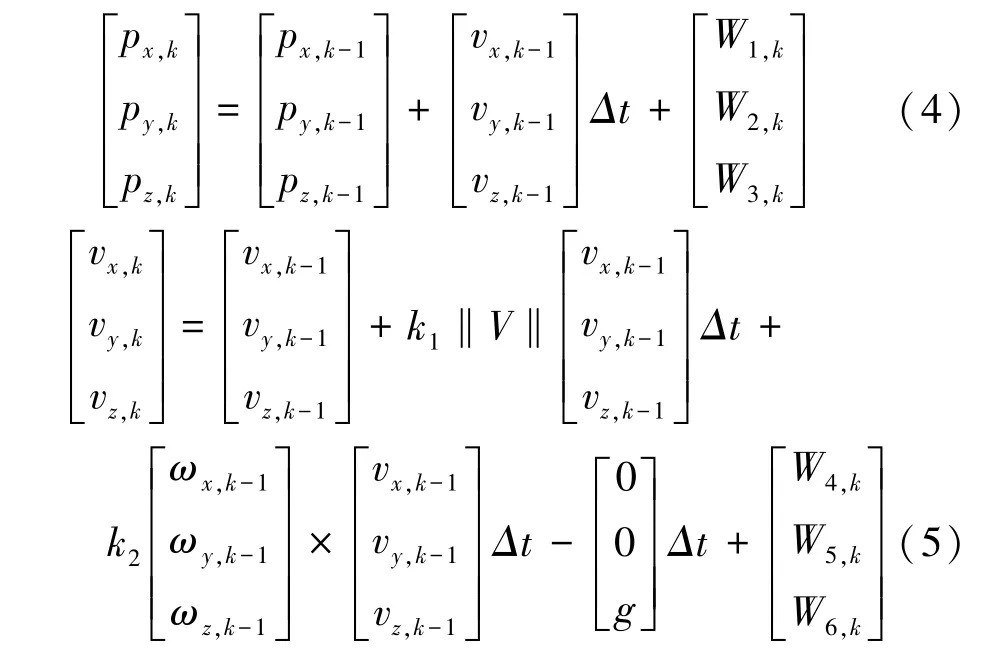
其中,W(1,2,3,…9)为时刻9维零均值过程噪声向量中的各项;系数为空气阻力因子;为马格努斯力因子;‖‖表示第1时刻3个方向线速度的模值。
进一步,研究推得的数学计算公式可写为:
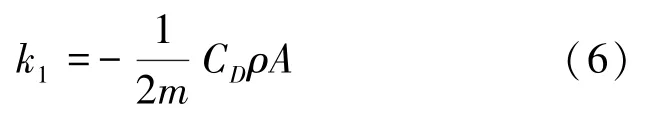
其中,C取决于乒乓球表面粗糙程度;为空气密度;为乒乓球最大横截面积。
同时,研究推得的数学计算公式可写为:
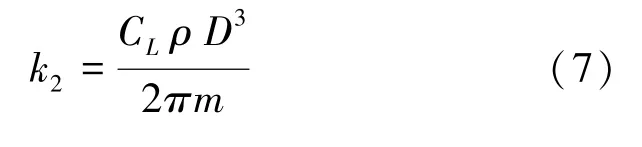
其中,C为升力系数;为乒乓球直径;为乒乓球质量。
综上可得,时刻乒乓球在,,坐标轴的角速度可由如下公式计算求得:
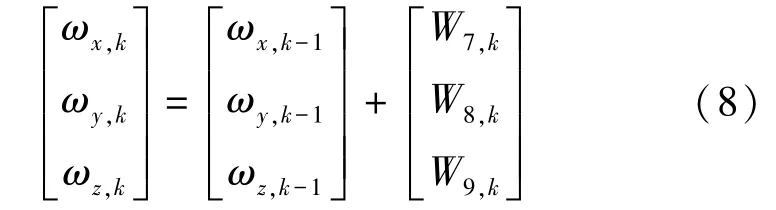
至此,乒乓球运动模型的系统过程方程构建完成。
1.1.2 系统观测方程研究
乒乓球运动模型的系统观测方程,表示形式为:
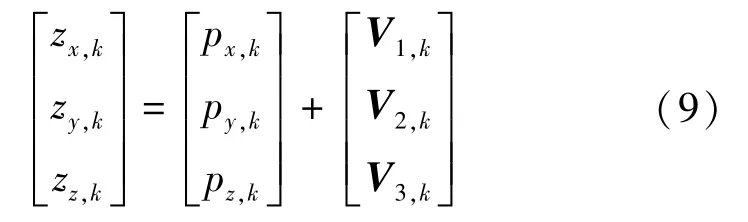
其中,V(1,2,3)为时刻三维零均值观测噪声向量。
W与V线性无关,且满足式(10):
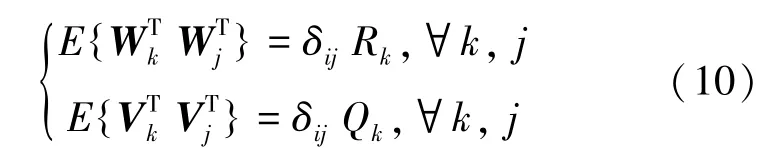
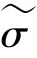
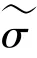
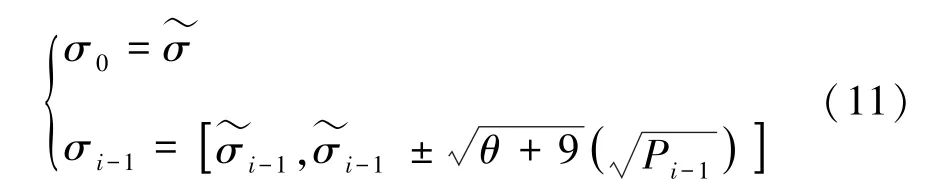
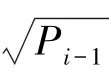
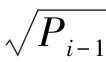

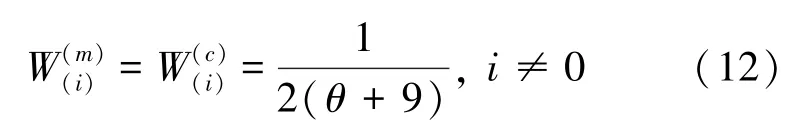
在这一部分,关于初始值的运算可给出研究表述如下。
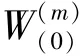

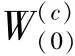
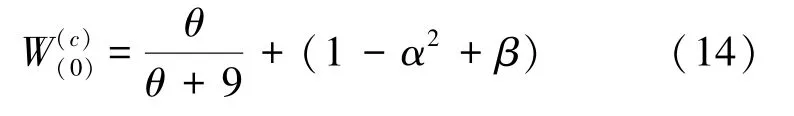
其中,表示采样点的分布信息。
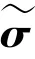

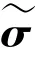
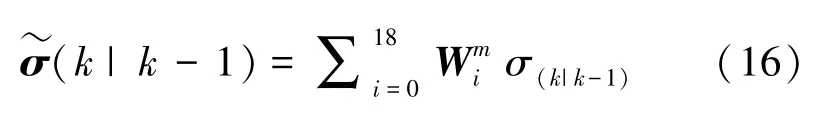
并计算下一步误差协方差(1),数学定义式如下:
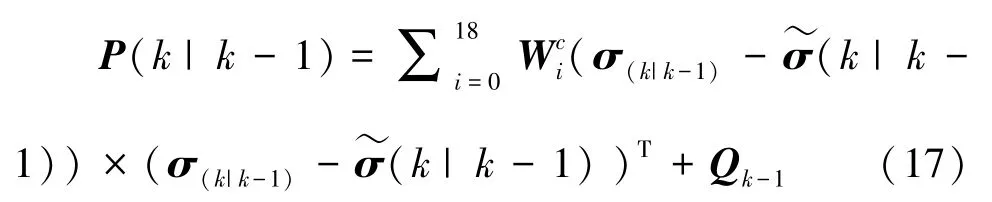

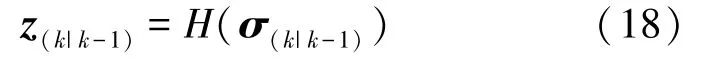
计算误差协方差(1),对此可写为如下形式:
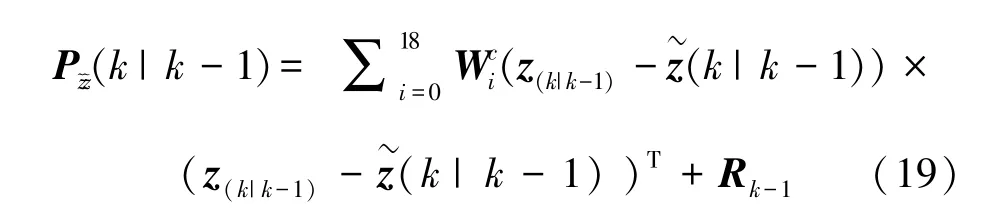
计算互协方差(1),可由下式确定:
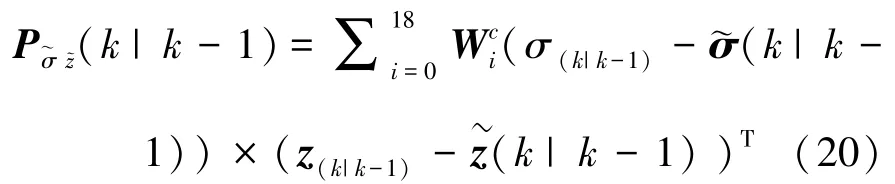
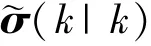

1.2 基于运动学的乒乓球碰撞后轨迹预测
快速地获取碰撞后乒乓球的轨迹,以便机械臂具有充足的时间调整姿态和位置将乒乓球击回,由于乒乓球碰撞后运动状态发生改变,碰撞后传统UKF乒乓球轨迹预测的收敛时间更长,预测误差逐渐增大。本文通过构建反弹后简单物理运动模型(SPM)的方式预测碰撞后的乒乓球轨迹。
由于带有马格努斯力的乒乓球物理运动模型构建复杂、且马格努斯力较小,在构建碰撞后的乒乓球物理模型时,忽略马格努斯力。乒乓球运动时的受力分析如图1所示。

图1 乒乓球运动时受力分析图Fig.1 Force analysis diagram during the moving of table tennis
图1中,F为乒乓球所受重力;F为空气阻力;C为空气阻力系数;F为空气浮力;为乒乓球的速度。
由于空气浮力数值太小,不加入后续模型推导计算。乒乓球所受各力的数学公式具体如下:
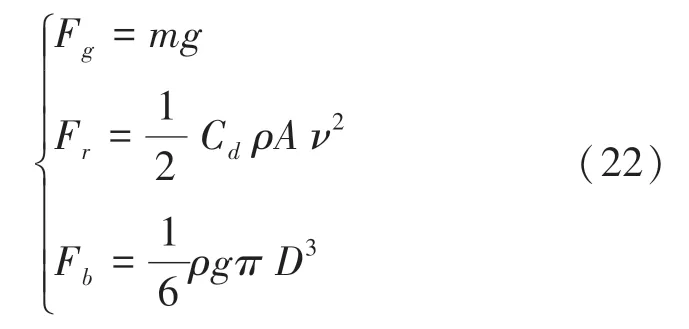
其中,C为空气阻力系数;为空气密度;为乒乓球最大横截面积;为乒乓球直径。
由于空气浮力数值太小,不加入后续模型推导计算。
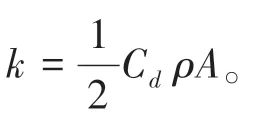

对式23()积分可得,时刻乒乓球在轴上的分速度v的数学公式可写为:
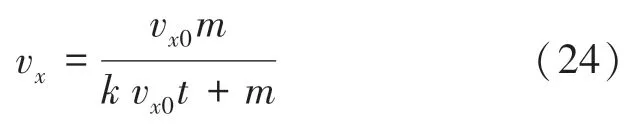
其中,v表示0时刻乒乓球在轴上的初始分速度。
乒乓球时刻在轴上分速度v,以及时刻乒乓球在轴的坐标p的计算公式分别如下:
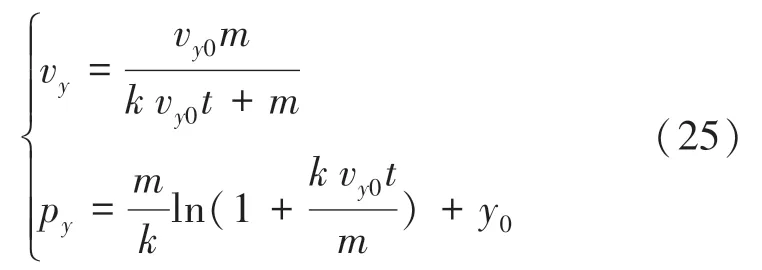
其中,v表示0时刻乒乓球在轴上的初始分速度,表示0时刻乒乓球在轴上的初始位置坐标。
乒乓球在轴方向受到空气阻力及重力的影响,当v>0时,根据乒乓球受力分析及牛顿第二定律可得式(26):

对式(26)积分可以得时刻乒乓球在轴上的分速度v的数学公式可写为:
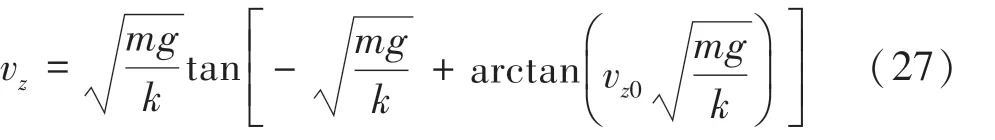
其中,v表示0时刻乒乓球在轴上的初始分速度。
对式(27)中的速度v在0时刻积分可得,时刻乒乓球在轴的坐标p,可由下式计算求得:

其中,表示0时刻乒乓球在轴上的初始位置坐标。
当v≤0时,根据乒乓球受力分析及牛顿第二定律可得式(29):
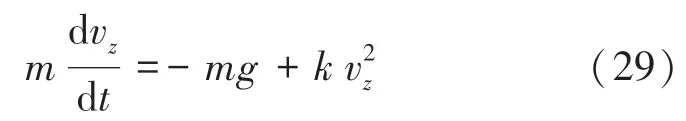
对式(29)积分可以得到:
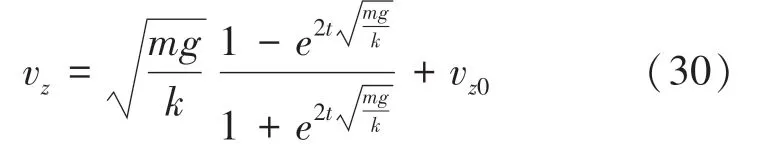
对式(30)中的速度v在0时刻积分可得,时刻乒乓球在轴的坐标p,运算公式见式(31):
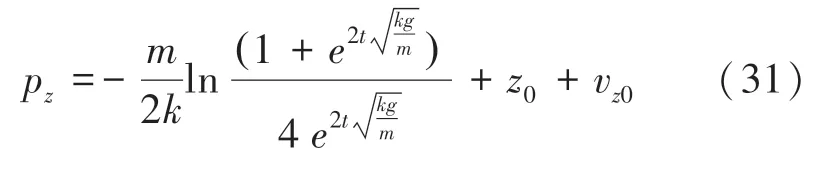
乒乓球与桌面发生碰撞时,由于球速、球的运动方式不同,在水平方向和垂直方向上的摩擦系数和衰减系数也不同。构建乒乓球的反弹模型,计算反弹后乒乓球在,,轴的速度v,v,v,推得的数学公式分别如下:
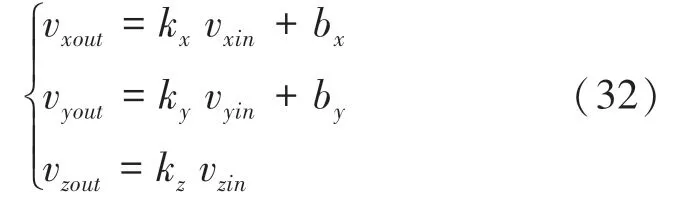
其中,k、k、k、b、b表示反弹拟合参数,v、v、v分别表示,,轴反弹前乒乓球的速度。
利用乒乓球碰撞反弹的轨迹拟合,采样多条乒乓球反弹轨迹,记录反弹前后坐标,利用最小二乘法拟合确定反弹拟合参数。
2 实验结果对比分析
在搭建高速运动的乒乓球系统中验证本文算法的有效性。乒乓球机器人系统中的图像采集设备为USB工业摄像机,帧率为120 fps。轨迹预测的数据采样时间间隔为20 ms。传统UKF方法与SPMUKF方法轨迹预测结果对比如图2所示。
由图2可知,传统UKF预测方法的结果在轴上误差不超过10 mm,、轴误差不超过20 mm。由于UKF算法需要测量值的输入不断修正状态估计量,从而更好地预测下一个点的位置,因此当只输入部分数据时,随着时间的推移,轨迹预测值会出现较大误差。而改进后的UKF乒乓球轨迹预测算法通过对物理模型的建模,在乒乓球反弹后的轨迹预测中整体误差有所降低,、轴方向误差在10 mm内,轴误差在15 mm内,相较于传统的UKF预测方法,误差有一定减少。
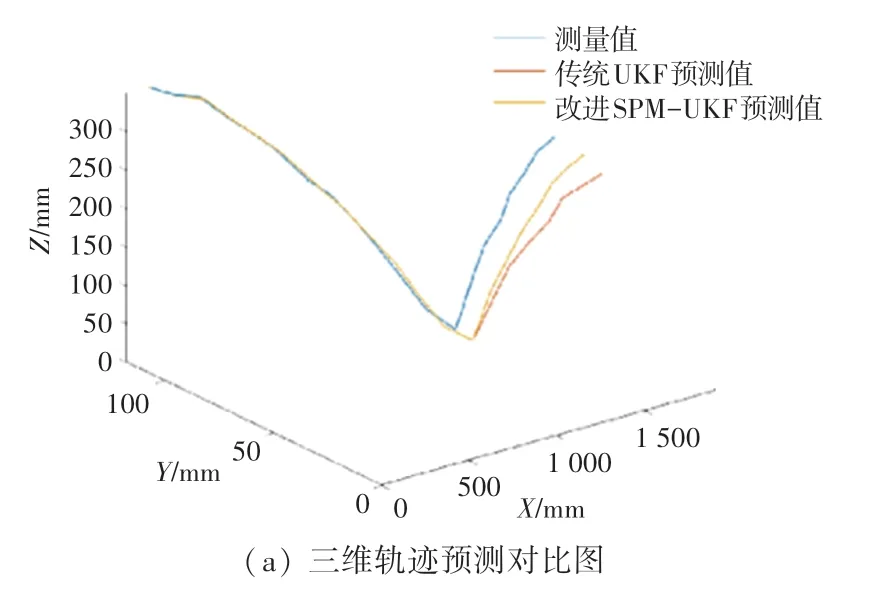
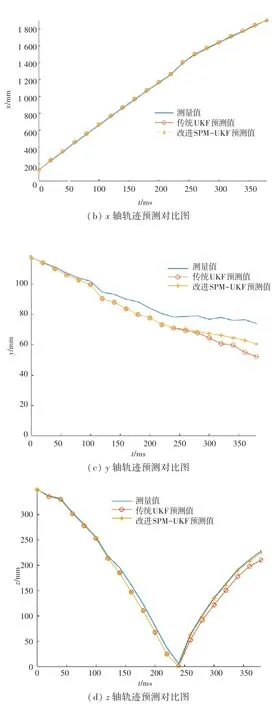
图2 不同算法结果对比图Fig.2 Comparison of results with different algorithms
3 结束语
本文针对传统的UKF算法在乒乓球碰撞后轨迹预测误差随时间增大的问题,提出了改进的UKF乒乓球轨迹预测算法。对乒乓球碰撞前的轨迹采用UKF算法预测,在碰撞后采用简单物理运动模型预测乒乓球的轨迹。实验证明改进的UKF乒乓球轨迹预测算法可以一定程度上提高轨迹预测的精度,为后续乒乓球机器人击球工作的开展提供了保障。

