基于GA-SVR的循环流化床锅炉床温预测

盛家豪，钱 进，2，王一桂，黄凤启

（1 贵州大学 电气工程学院，贵阳 550025；2 重庆大学 动力工程学院，重庆400044；3 中国电建集团贵州工程有限公司，贵阳 550025；4 国投盘江发电有限公司，贵州 盘州 553000）

0 引 言

中国“双碳”目标及实现能源结构转型的提出，使传统化石燃料发电行业面临严峻挑战。循环流化床（Circulating Fluidized Bed，CFB）锅炉具有燃料适应性广、可掺烧生物质、降负荷比大、碳排放强度及其他有害污染物排放量相对较低等优点。在未来新能源、可再生能源为主的能源供应结构中，必将作为深度调峰、旋转备用的主力，确保CFB锅炉经济可靠运行研究有重要意义。

CFB锅炉床温是影响CFB锅炉经济、高效、安全运行的重要参数之一。床温过高，会导致锅炉的热传导增快，受热面温度过高，引起高温结渣腐蚀和超温爆管等问题，同时也会导致NO排放量增加；而床温过低将引起锅炉热效率降低，锅炉汽水参数不达标，底渣和飞灰中可燃物含量增高，从而影响锅炉的经济运行。因此，一些国内外学者对CFB锅炉的床温特性进行了大量的建模研究。基于机器学习和神经网络等技术建立的分布参数、时变、非线性、多变量紧密耦合控制对象的动态模型具有较好的自适应能力和泛化能力，在电站锅炉运行及污染物排放控制建模方面得到了广泛的应用。尤海辉等人提出基于减法聚类的模糊神经网络模型预测循环流化床入炉垃圾热值。钱虹等人实现了基于深度循环神经网络的SCR烟气脱硝系统出口NO排放预测。白建云等人构建了基于BP神经网络的NO质量浓度在线测量模型。张妍等人利用粒子群优化粒子滤波算法实现了循环流化床床温预测。但上述方法存在所需基础数据量大、模型复杂、训练和计算时间长、精确度不高等问题。对于小样本数据，段萌等人提出基于卷积神经网络的小样本图像识别方法。王琦等人建立基于BPSVM的SO特性模型，实现对SO浓度的快速、准确预测。

本文在分析CFB锅炉运行机理的基础上，从小样本容量数据预测出发，结合已有数据，选择合适的模型输入变量，通过GA算法对SVR的重要参数进行全局寻优，构建CFB锅炉床温预测模型，将GA-SVR模型与BP神经网络、BP-SVR和CNN模型分别进行性能对比分析，以实现对某300 MW CFB锅炉的床温预测。

1 遗传算法和支持向量回归原理

1.1 遗传算法

遗传算法（Genetic Algorithm，GA）源自对自然界物种繁衍进化的数学和计算机模拟研究。遗传算法本质上是一种高效、并行、全局搜索的方法，能在搜索过程中自动获取和积累有关搜索空间的知识，并自适应地控制搜索过程以求得最佳解。其一般步骤为：

（1）编码及初始化。将所需求解的数据集编译成遗传空间的基因型串结构数据集，并随机生成原始种群。

（2）适应度评估。选择一个评判基因优劣的指标函数作为遗传算法的适应度，计算种群所有个体的适应度。

（3）个体筛选。通过轮盘赌法保留评价指标高的个体。

（4）遗传操作。对经筛选保留的各个体基因进行交叉和变异操作，产生子代个体，形成新一代种群。

（5）准则判断。根据设定的准则、如迭代次数和指标大小判断GA算法是否继续执行。若执行算法，则返回步骤（2）；否则进行全局搜索，找出所有子代中适应度最高的个体作为算法的最优解。

1.2 支持向量回归

支持向量机（Support Vector Machine，SVM）是一类按监督学习方式对数据进行二元分类的广义线性分类器，而支持向量回归是在SVM的基础上，针对回归问题而衍生出来的算法。对于样本（，），传统回归模型的预测误差为模型预测值与数据真实值的差值，而SVR能容忍预测值（）与真实值之间最多有的偏差，即仅当（）与之间的差别绝对值大于时才计算损失，于是SVR问题可形式化为式（1）：

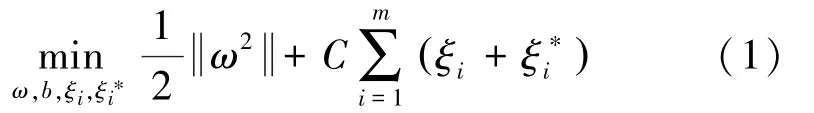
约束条件为：

其中，式（1）的第一项为最小化结构风险，第二项为经验风险，是对二者进行折中的常数，设为惩罚系数；ξ、为松弛变量；为损失边界，可设为损失函数。

求解可用拉格朗日乘子法转为对偶问题，研究推得的数学公式可写为：

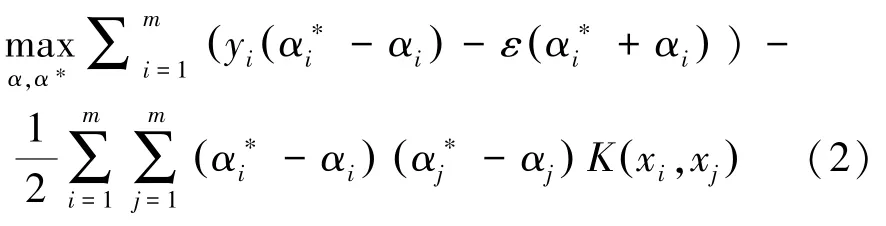
约束条件为：

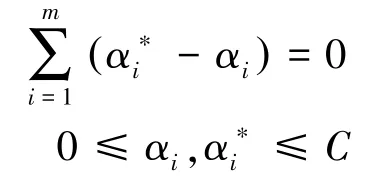
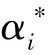
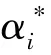
2 床温的GA-SVR预测模型

本文研究对象为某300 MW循环流化床锅炉，选择床温预测模型的输入变量和输出变量，进行数据预处理；通过遗传算法对SVR参数进行全局寻优；采用最佳参数训练SVR，最终将模型用于床温预测。

2.1 床温特性分析

CFB锅炉床温的高低主要由其运行参数、如给煤量、一次风量、二次风量、循环灰量等决定。

对于同一煤种，一次风量和循环灰量不变时，床温与给煤量保持一致的变化趋势。而给煤量不变时，一次风量的增加能促进密相区燃料的燃烧热解，但也会增大烟气携带床料的固体热损失，同时由于一次风温较低，过量的一次风也会冷却床层，使床温下降；而一次风量过低，无法提供燃烧热解所需氧量，密相区过度缺氧燃烧，导致床温降低。此外一次风量过小，可能无法维持床层的正常流化状态，将严重威胁CFB锅炉的安全运行。二次风的作用是保证稀相区挥发分和残碳的正常燃烧，稀相区氧量充足时，因二次风温相对于稀相区整体的温度偏低，二次风量的增加，将冷却烟气和流化物料；当稀相区氧量不足时，提高二次风量能促进挥发分和残碳的燃烧，提高烟气和流化物料温度，而少量烟气和物料经旋风分离器分离后又将返回密相区，从而可间接影响床温。而循环灰量增加时，循环灰从炉膛底部带离的热量增加，从而降低床温；循环灰量不足时，床层热量无法被及时带离，将导致床温升高。

2.2 模型数据

本文基于某300 MW循环流化床锅炉机组变负荷工况下的运行数据，从锅炉运行机理和床温特性分析出发，选择负荷（）、锅炉总烟气流量（）、烟气氧含量（）、石灰石颗粒给料量（）、给煤量（）、热一次风温（）、热二次风温侧（）、热二次风温侧（）、一次风总量（）、二次风侧总量（）、二次风侧总量（）、粉尘排放量（）作为模型的输入参数，炉膛平均床温（）作为输出参数。先对样本进行粗大误差处理，筛除数据坏点，选取连续9天内锅炉机组的216组数据后再以6：4的比例，将运行数据随机划分为训练集和验证集。部分数据见表1。

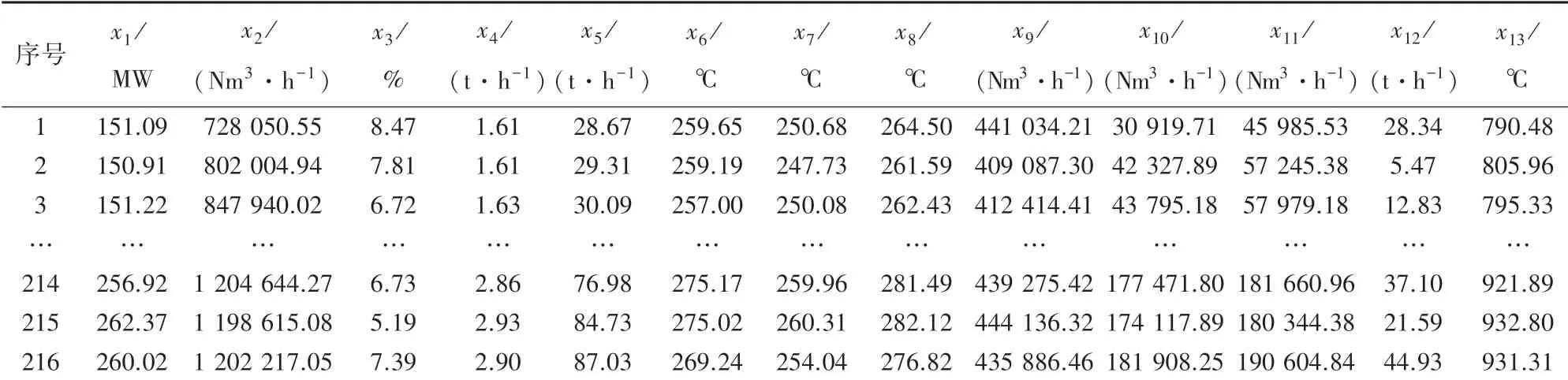
表1 某300 MW循环流化床锅炉运行数据Tab.1 Operation data of a 300 MW CFB boiler

2.3 模型建立

（1）数据预处理：在参数寻优和SVR建模前，需将所选的运行数据无量纲化，以消除各数据量纲的影响。本文选择归一化处理各输入变量，数学定义公式见如下：

其中，为某变量空间；为变量空间中最小的值；为变量空间中最大的值。训练集和验证集的输入输出变量均经过归一化处理后映射到［0，1］区间内。

（2）SVR参数寻优：建立预测模型前，需确定SVR的相关参数，以保证模型的准确性。本文采用遗传算法，对其3个主要参数：惩罚系数、径向核参数（x，x）和损失函数全局寻优。以确定系数（R-Square）为遗传算法的适应度，再设置SVR为待优化函数，并绑定所需优化的参数、和（x，x）；设置参数的区间范围并确定初始值：2，0.5，（x，x）1。规定遗传为40代，每代20人，并按照步骤计算，最终得到最优化参数7840 8，0.013，（x，x）0.299 7。遗传算法每代适应度值如图1所示。

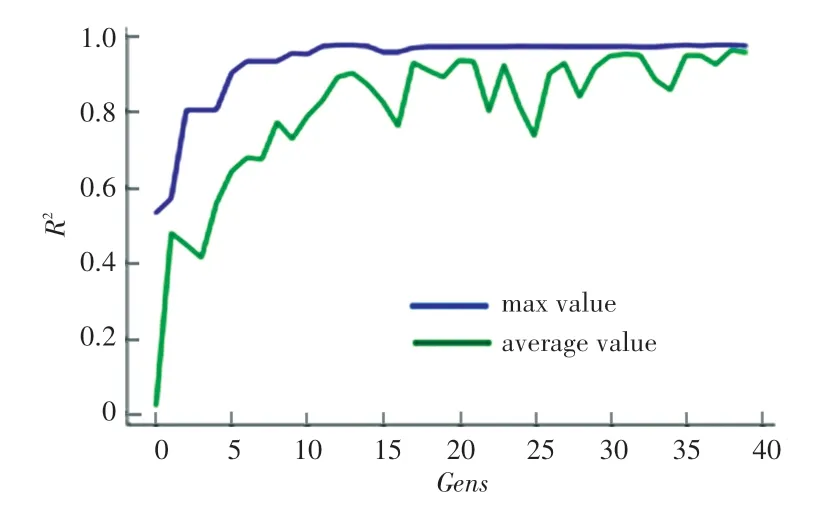
图1 遗传算法适应度Fig.1 Fitness of genetic algorithm per generation

（3）SVR建模：将经过归一化处理的数据集，，……，作为GA-SVR模型的输入，将锅炉平均床温作为模型的输出，建立锅炉床温的GA-SVR预测模型。

3 预测结果与模型对比

GA-SVR模型对验证集的预测结果如图2所示。

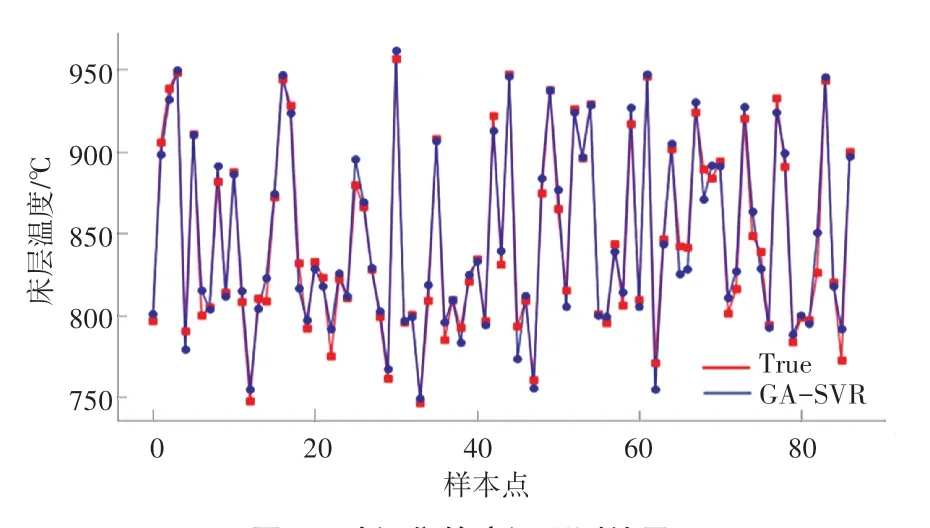
图2 验证集的床温预测结果Fig.2 Bed temperature prediction results of the verification set

选取确定系数（R-Square）、均方误差（）、模型计算时间为模型的评价指标，具体数学定义公式分别如下：

在研究运行后可得到基于GA-SVR的CFB锅炉床温预测模型的确定系数为0.977 6，均方误差为0.16%，计算时间为0.008 9 s，验证集的最大预测误差为24.4℃。

为验证GA-SVR模型对于小样本数据预测的优越性，本文将GA-SVR模型与BP神经网络、BPSVR和CNN三种常用预测模型进行了对比。对此拟展开分述如下。

3.1 GA-SVR与BP神经网络预测结果对比

本文采用常见的单隐层BP神经网络结构，将12个运行参数作为输入变量，按经验公式计算得出隐层神经元参考个数为10，以CFB锅炉床温作为输出变量，选取为损失函数，函数为各神经元的激活函数，网络总迭代次数为1 000次，建立了基于BP神经网络的床温预测模型。将BP模型与GA-SVR模型的预测误差和评价指标进行对比，具体如图3所示。各指标对比结果见表2。

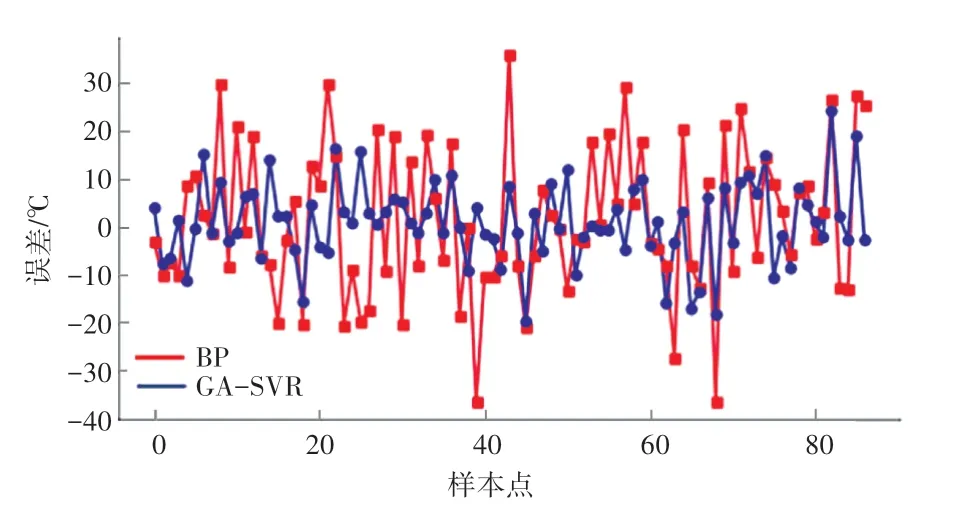
图3 BP模型与GA-SVR模型预测误差对比Fig.3 Comparison of prediction errors between BP model and GA-SVR model

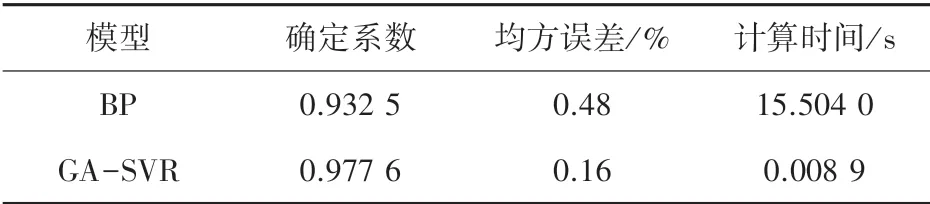
表2 BP模型与GA-SVR模型评价指标对比Tab.2 Comparison of evaluation indexes between BP model and GA-SVR model

由图3和表2可知，对于同一验证集，GA-SVR模型预测误差分布较为均匀，几乎全部样本点的预测误差都小于BP模型预测误差；GA-SVR模型的最大误差为24.4℃，相较于BP模型的37.2℃也有了明显的降低；GA-SVR模型的各项评价指标明显优于BP模型。尤其是时间指标，BP模型的计算时间为GA-SVR模型的1 742倍。

3.2 GA-SVR与BP-SVR预测结果对比

将BP神经网络与支持向量机结合，对输入变量进行影响力分析计算，筛除影响力小于5%的输入变量，再将降维后的变量作为SVR模型的输入。为保证模型间具有可比性，对SVR参数也进行寻优，建立BP-SVR的CFB锅炉床温预测模型。BPSVR与GA-SVR模型预测误差与评价指标对比，具体如图4所示。各项指标对比结果见表3。

表3 BP-SVR模型与GA-SVR模型评价指标对比Tab.3 Comparison of evaluation indexes between BP-SVR model and GA-SVR model

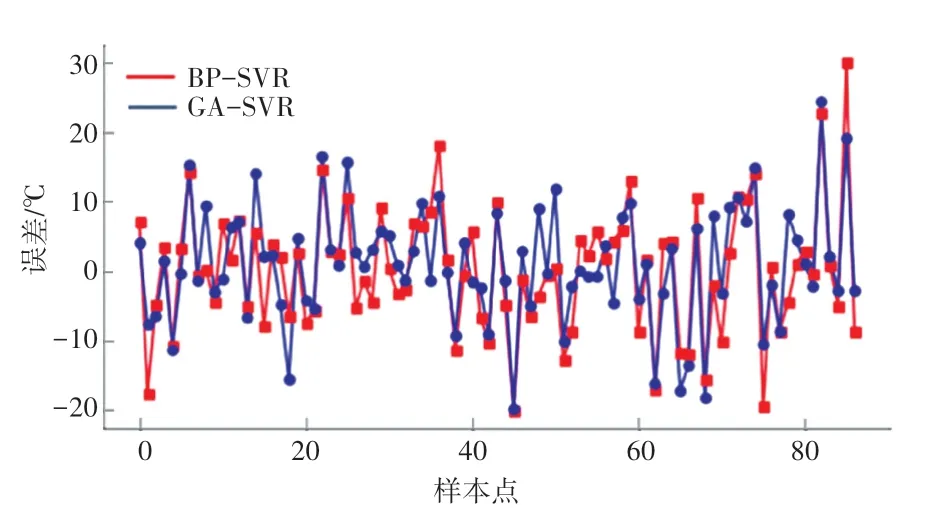
图4 BP-SVR模型与GA-SVR模型预测误差对比Fig.4 Comparison of prediction errors between BP-SVR model and GA-SVR model

由图4和表3可知，BP-SVR预测模型与GASVR预测模型的误差主要集中在［-10℃，10℃］区间内，两模型预测折线图整体差异不大，均能较好反映床温真实值。GA-SVR模型的和指标略优于BP-SVM模型，但BP-SVR模型的计算时间有了一定的改善。BP-SVR模型在部分样本点的预测结果与真实值存在较大偏差，精度较低，其最大误差为30.1℃，高于GA-SVR模型的24.4℃，表明输入变量维度的减少能降低模型的复杂程度，提高模型计算速率，但也会损失部分数据信息，造成模型精度的轻微下降。

3.3 GA-SVR与CNN预测结果对比

本文选择的CNN模型采用LeNet-5结构，即2卷积层／2池化层／2全连接层，设定卷积层1和2的卷积核个数均为40，卷积核尺寸为33；全连接层1和2的神经元个数分别为20和10；选取池化函数为最大值函数，激活函数为函数，训练次数为40次，建立CNN的CFB锅炉床温预测模型。CNN与GA-SVR模型预测误差与评价指标对比，具体如图5所示。各指标对比结果见表4。

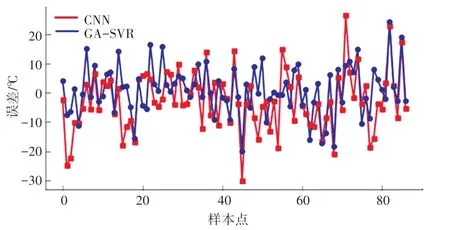
图5 CNN模型与GA-SVR模型预测误差对比Fig.5 Comparison of prediction errors between CNN model and GA-SVR model

表4 CNN模型与GA-SVR模型评价指标对比Tab.4 Comparison of evaluation indexes between CNN model and GA-SVR model

由图5和表4可知，从整体上看CNN模型预测误差相比GA-SVR模型有负误差增大的情况，且预测误差折线图的波动较大，存在多个误差大于20℃的样本点，最大误差为30.0℃，也高于GA-SVR的24.4℃。从评价指标上看，CNN模型的评价指标和均劣于GA-SVR，且预测所需时间更长。

4 结束语

本文通过GA遗传算法精确且快速地对SVR算法的惩罚系数、径向核参数（x，x）和损失函数全局寻优，能有效解决SVR算法最优参数选取困难的问题。对于同一测试样本，分别建立基于BP神经网络、BP-SVR和CNN的床温预测模型，并预测同一验证集，得出GA-SVR、BP神经网络、BPSVR和CNN四种预测模型的最大绝对误差分别为：24.4℃、37.2℃、30.1℃和30.0℃，最大相对误差分别为：2.4%、4.4%、3.8%和3.7%；通过比较分析4种模型的评价指标和误差可得出面向小样本数据容量，GA-SVR预测模型拥有更高的预测精度和更低的时间成本，因此面向小数据样本容量的GA-SVR循环流化床锅炉床温预测模型能实现对CFB锅炉床温的实时准确预测，具有较好的工程应用价值。