变压器集成级联混合无功补偿设备研究

张永熙，朱亮亮，柯振宇，白祥宇，杨胜林

（国网新疆电力有限公司乌鲁木齐供电公司，新疆 乌鲁木齐 830000）

0 引言

电网事业蓬勃发展，电力电子技术应用场景越来越广泛，随之而来的电能质量问题越来越多［1］。如今，针对无功补偿与谐波抑制，级联H桥静止无功发生器（Static Var Generator，SVG）应用十分广泛，但由于使用大量的电力电子器件［2］，存在成本较高的问题；而传统的静止无功补偿器（Static Var Compensator，SVC）由于响应速度较慢，补偿效果不理想等原因，亟须改进。

由于接入点电压较高会加大初始投入，文献［3］运用耦合变压器的方式，一定程度上降低了电压问题，与此同时增加了设备体积和运行损耗，变压器损耗更是占系统损耗的40%以上。文献［2］引入了具有无源支路的补偿，无源支路用于补偿大额无功，综合成本有所下降，但这也同时牺牲了动态补偿范围。文献［4］通过接入级联结构的SVG，有效提升了补偿性能，但并未考虑运用大量SVG所带来的成本问题。文献［5］对变压器抽头注入无功补偿系统进行原理分析，建立了三绕组自耦变压器的相量模型，得到注入电流后绕组电流的分布规律，并对控制系统的设计提出了指导意见。专利［6］提出了一种混合级联桥式变流电路在静止无功补偿器领域的应用，该专利的应用在产生相同电平数时，使用的电子器件更少，更有利于静止无功发生器的推广应用。文献［7］提出了一种基于小波包分解与重构算法的谐波电能计量方法，通过仿真验证了小波包分解算法在该领域的可行性与准确性，为分析电能质量数据提供了新的思路。文献［8］通过对现有负载无功指令的频率及补偿装置的补偿性能分析，提出一种功率分解的混合无功补偿方案，但面对大额高频变化的无功负载时，小容量的SVG并不能及时对负载进行补偿。文献［9］通过对LC 及SVG 补偿特性分析，提出一种基于模糊-改进型比例积分（Proportional Integral，PI）双模控制器及SVG 与LC 之间的协同调节策略，能够对系统进行补偿，但并未从本质上对LC于SVG进行区分。

提出将成本低廉的新型补偿结构纳入级联结构的SVG中，提出级联混合无功补偿设备，并将其接入变压器高压侧进行集中补偿。针对负荷特性，考虑电力电子器件的耐压水平与成本经济性的因素，选取合理的变压器抽头。合理利用变压器抽头，可以降低接入电压，从而极大地节约成本。针对无功补偿设备自身性能，提出基于瞬时功率理论的功率分解方案，将高频功率分配给SVG 进行补偿，低频功率分配给新型结构补偿。针对系统无功需求波动较大且需求特性不同，提出自适应控制算法，提升系统鲁棒性。

1 系统电路结构与补偿原理

1.1 系统电路结构

变压器联接方式较多，在众多联结形式中，DYn11 联结有较好的不平衡运行能力，对高次谐波抑制作用也较为突出［5］，因此得到了广泛的应用。针对DYn11 联结变压器特点，提出一种变压器集成级联混合无功补偿设备的电路结构，如图1所示。

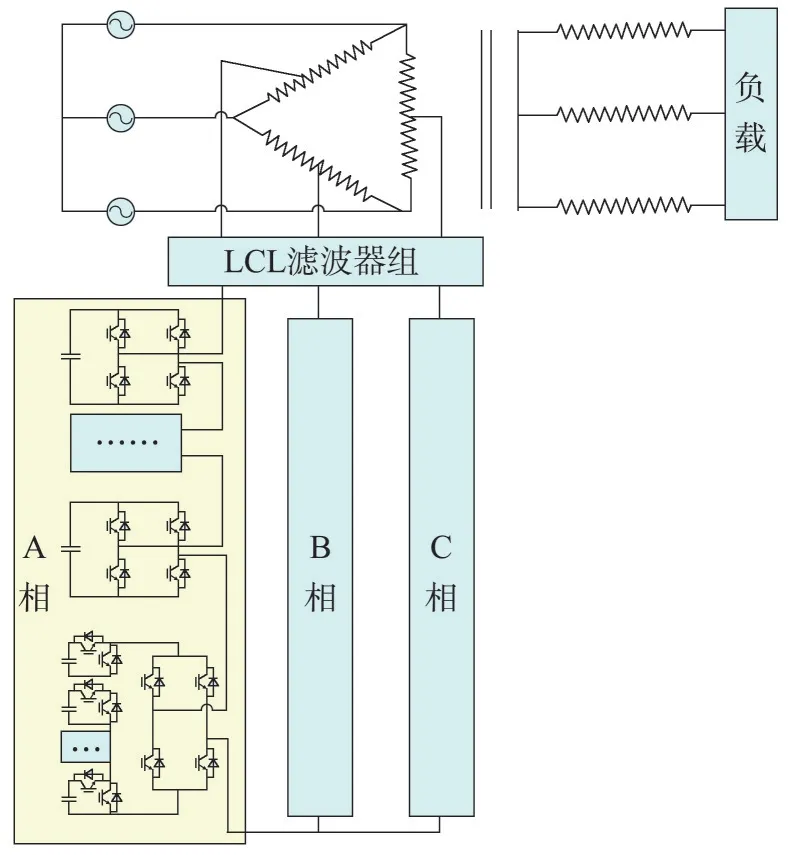
图1 变压器集成级联混合无功补偿设备结构

级联混合无功补偿装置经过三组LCL 滤波器与变压器高压侧ABC 三相上的绕组抽头相连，为保证混合无功补偿设备补偿的三相电压对称，需三相抽头位置对称。选择星型连接方式，新型补偿结构［6］上层采用H桥，下层将各半桥子模块进行级联。

1.2 补偿原理

为能够更加清晰表达无功补偿系统的工作原理，根据上述电路结构，可建立系统稳态运行的等效模型，混合无功补偿系统此时可看作一个整体，可将无功补偿系统用受控电流源等效。ISE、ISF、ISG分别代表补偿电流，Ita、Itb、Itc分别代表网侧电流，Iua、Iub、Iuc分别代表负载侧电流，等效模型如图2所示。

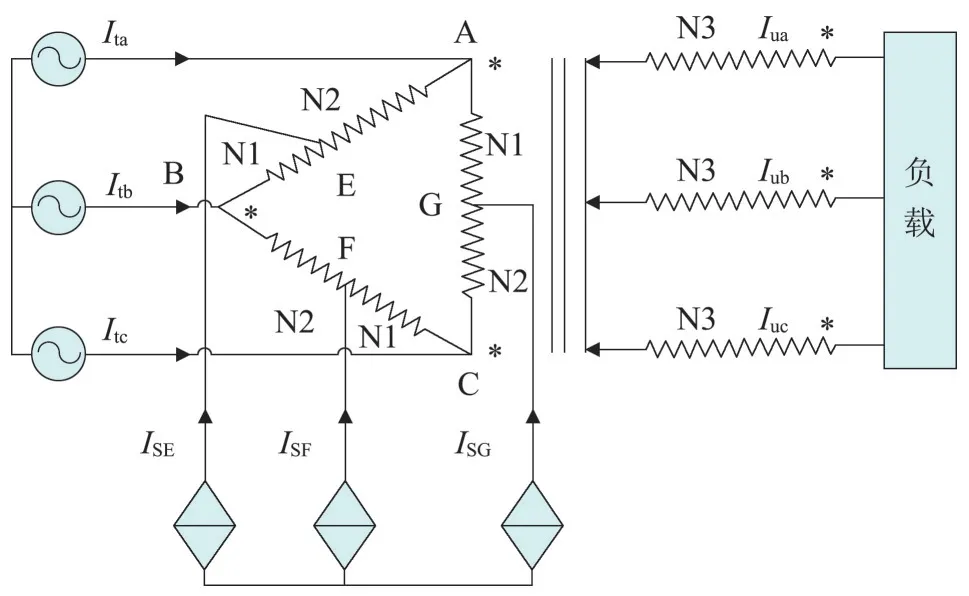
图2 等效电路模型

将补偿系统等效为受控电流源［2］，由瞬时无功功率理论，在对称三相交流系统中，无功补偿系统输出的瞬时功率在dq坐标下可表示为

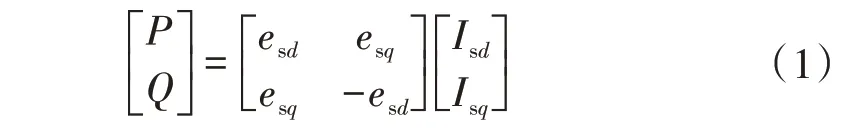
式中：P、Q分别为瞬时有功功率与无功功率；esd为静止坐标下系统侧有功电压；esq为静止坐标下系统侧无功电压；Isd为静止坐标下补偿系统补偿的有功电流；Isq为静止坐标下补偿系统补偿的无功电流。

将系统离散化，设系统采样周期为Ts，远小于电网频率，可假定相邻两个采样周期的数据相等，可知k时刻瞬时功率变化量为

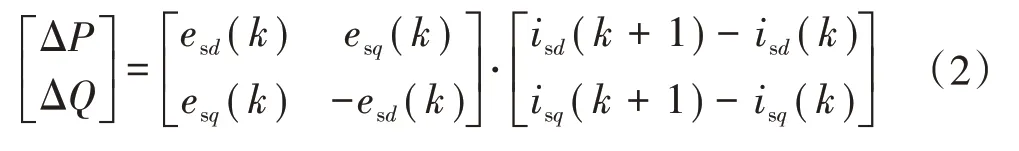
式中：isd(k)为k时刻静止坐标下补偿系统补偿的有功电流值；isq(k)为k时刻静止坐标下补偿系统补偿的无功电流值。差分电流可表示为

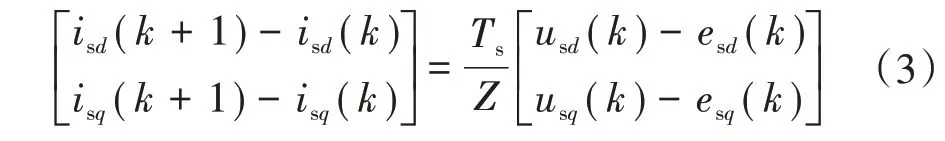
式中：Z为电路阻抗；usd(k)为k时刻静止坐标下补偿系统发出的有功电压值；usq(k)为k时刻静止坐标下补偿系统发出的无功电压值。

式（2）和式（3）化简可得

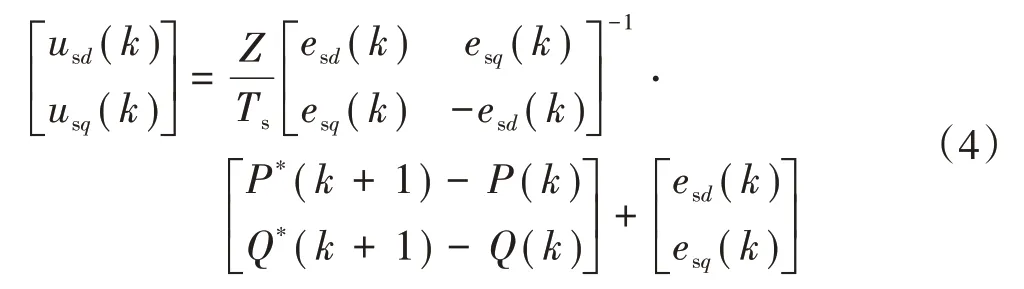
式中：P*(k+1) 为k+1 时刻的有功功率值；Q*(k+1)为k+1时刻的无功功率值。

由式（4）可知，电网电压不变，若得到瞬时功率变化量，就可得补偿系统的调制信号，即可实现系统对补偿功率的动态控制。

控制系统中采用自适应PI控制器，将瞬时有功无功的误差信号ΔP、ΔQ引入控制器，通过自适应PI控制器产生静止坐标系下的电压分量ud、uq，逆park转换后，经改进的单载波调制输出控制信号，对系统进行补偿。

2 基础理论方法

2.1 功率分配

在直接功率控制中，功率信号是通过瞬时功率计算得出的瞬时有功功率P和瞬时无功功率Q。根据SVG 与新型结构的性能，新型结构成本低廉，可用于补偿低频大容量无功，而考虑H 桥在级联结构中的分压作用，可使用H 桥补偿高频小容量无功。频率与时间的关系为

式中：F为频率；t为时间。

将小于25 Hz 的功率信号定义为低频功率［8］，将大于等于25 Hz的功率信号定义为高频功率，低频功率分配给新型结构进行补偿，高频功率分配给SVG进行补偿。

2.2 自适应PI控制器

粒子群算法中，粒子速度与位置更新公式为：

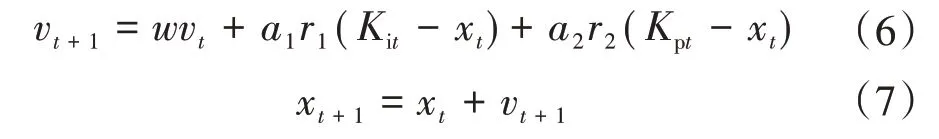
式中：xt为t时刻的粒子位置；vt为t时刻的例子速度；wt为t时刻的惯性因子；a1、a2为加速常数；r1、r2为在［0，1］之间的随机数；Kit、Kpt为粒子最新的最优位置。

基于粒子群算法的PI 控制器（Proportional Integral Controller Based on Particle Swarm Optimization，PSO-PI）控制器过程如图3所示。

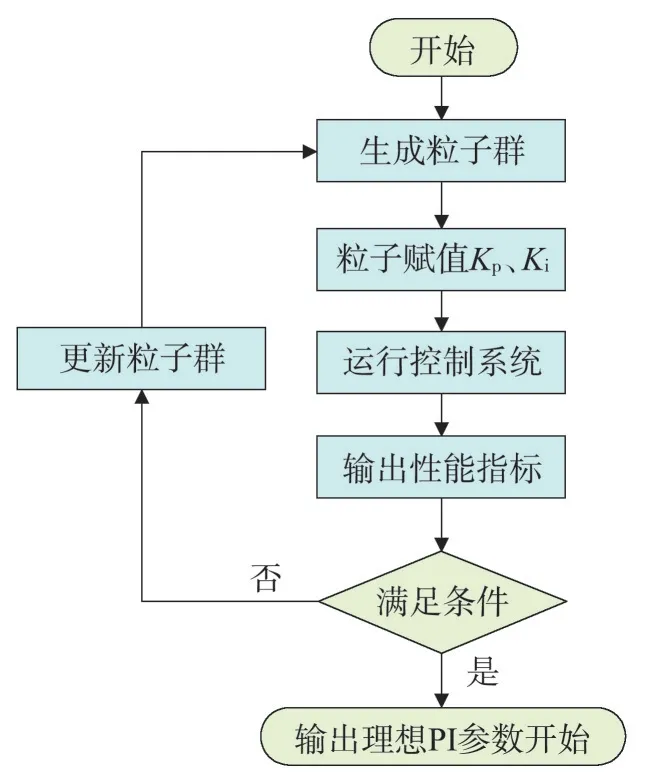
图3 粒子群优化PI参数流程

所采用的自适应PSO-PI 控制器，可间歇式自动调整控制参数［10］，调整过程如图4所示。

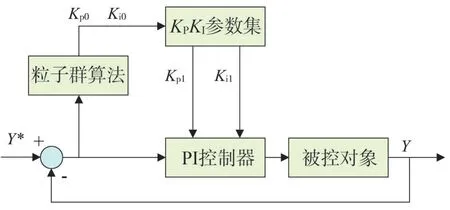
图4 自适应调整过程

图4 中，Y*为输入指令值，Y为输出值，为验证PSO-PI 控制器性能，设被控对象为纯积分环节，传递函数G0为

式中：K为常数。

PI环节的闭环传递函数为

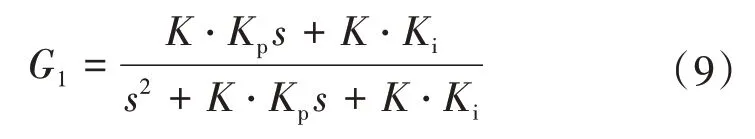
传统PI 控制参数为一固定常数，则固定PI 控制器与PSO-PI 控制器的阶跃响应曲线对比如图5所示。

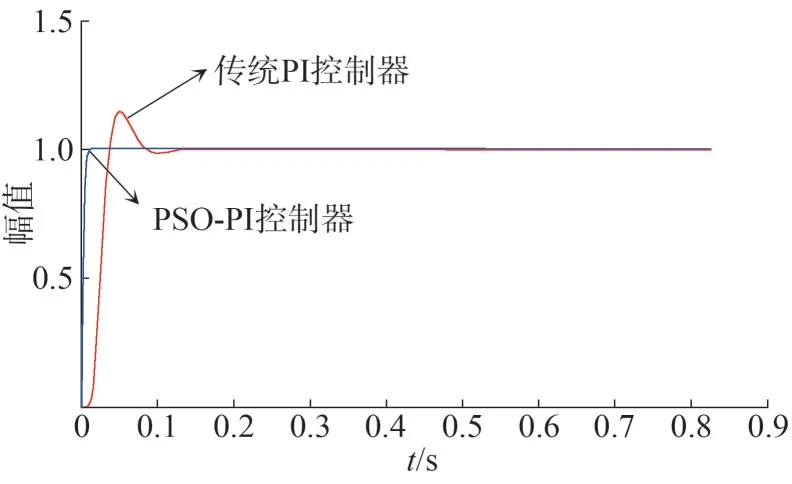
图5 固定PI控制器与PSO-PI控制器的阶跃响应曲线

由图5 可知，相比传统PI 控制，超调量减少约30%，传统型PI 控制大约在0.6 s 达到稳定，而PSOPI则在0.1 s就达到了稳定，可见PSO-PI控制器在响应速度与超调量上相较于传统PI控制器均由明显的优势。

PSO 算法在动态优化过程中，由于PI 参数有传统的经验值，可选取合适的寻优范围，通过调整粒子群规模，减少动态计算时间，在MATLAB.2016b 中，粒子群规模M=100、M=200、M=300、M=400 时的动态计算时间和阶跃响应对比如表1和图6所示。

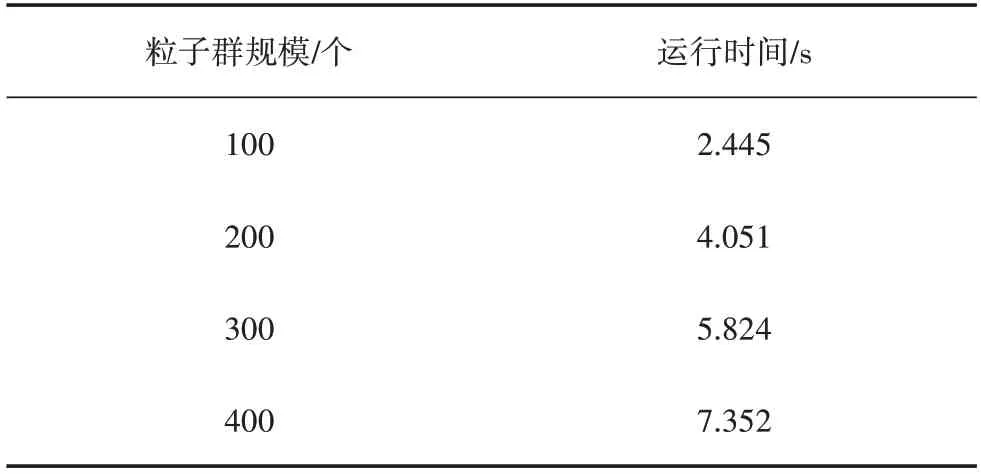
表1 PSO动态计算时间

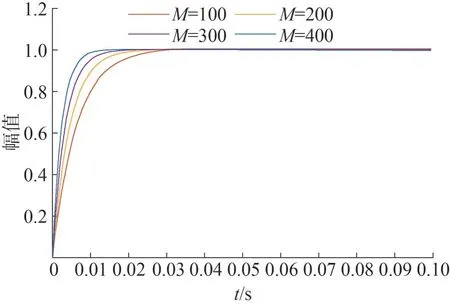
图6 阶跃响应对比

由表1 可知，随着粒子群规模的扩大，运行计算时间越来越大；由图6 可以看出，虽然粒子群规模对阶跃响应有一定影响，但影响相对有限，通过选取适当的粒子群规模，可以在一定程度上控制粒子群算法的运算时间。

3 补偿系统总体控制策略

补偿系统控制部分主要包括两部分：瞬时功率检测与分解部分，直接功率自适应控制部分。瞬时功率检测［2］与分解部分旨在通过对瞬时功率的高低频分解，再合理分配给SVG与新型结构，以提升补偿系统的经济性；直接功率自适应控制部分，采用自适应PSO-PI 控制器，旨在提升系统动态响应能力，使系统具有较高的鲁棒性。

3.1 瞬时功率检测与分解

采用Mallat 算法对瞬时功率进行分解，针对级联结构的系统，可将分解后的功率数据重构后分别传递给SVG与新型结构，流程如图7所示。

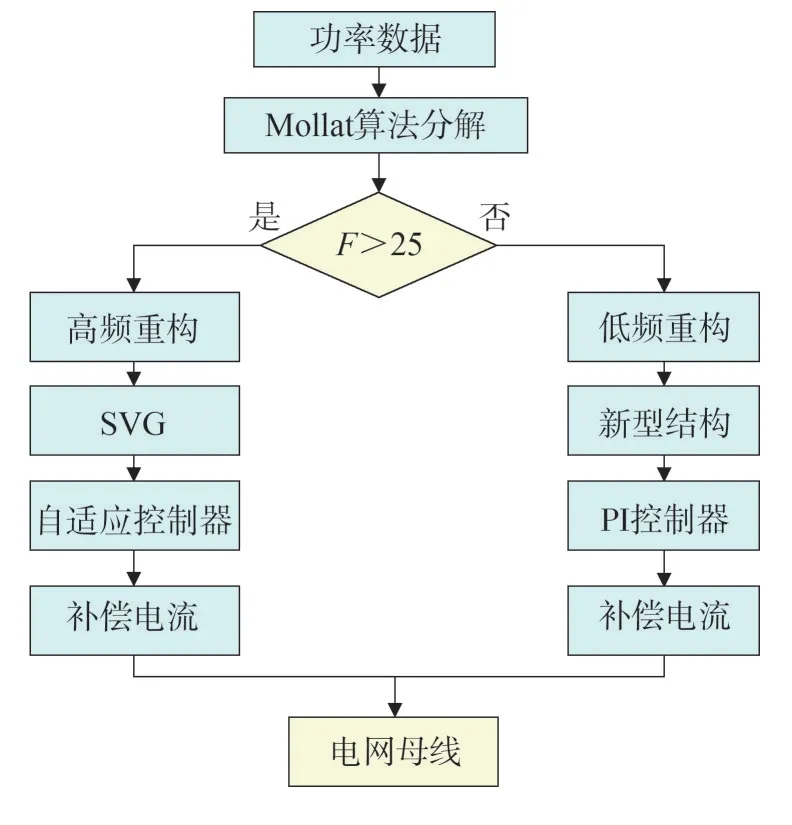
图7 级联系统控制流程

3.2 直流侧均压控制

直流电容均压问题，是链式SVG 正常工作的基础，也是链式SVG的关键技术。只有各直流侧电压稳定在给定值附近［11-17］，系统才能稳定运行，直流侧控制如图8所示。

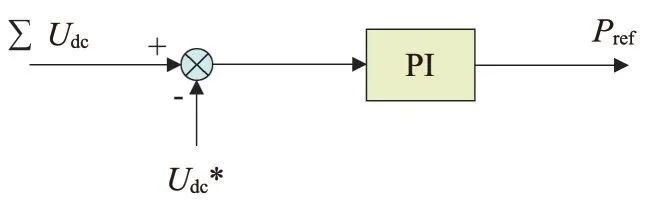
图8 直流侧控制

图8 中，Pref为有功功率指令值，∑Udc为各相直流侧电压之和，Udc*为直流侧电压的给定值，二者经过PI 控制即可得到有功指令信号，为了维持直流侧电压均衡，需将该信号叠加逆变器输出的有功分量上，确保直流侧与交流侧的能量转换。

相间均压控制如图9所示。

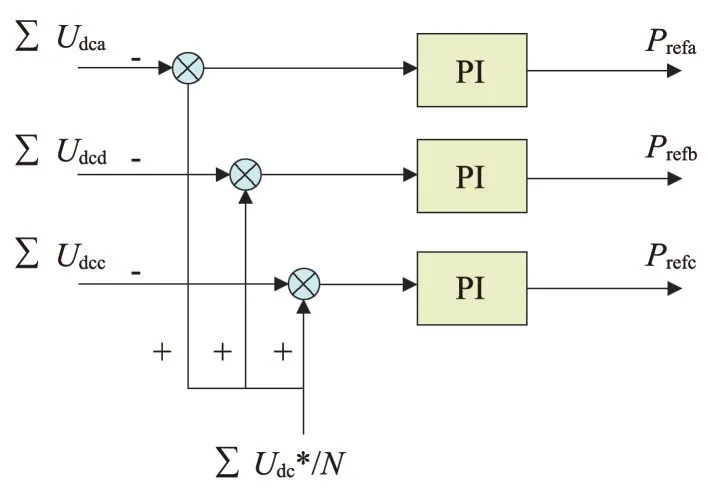
图9 相间均压控制

图9 中，∑Udca、∑Udcb、∑Udcc分别为A 相、B 相、C相直流侧电压的和，∑Udc*为三相直流侧电压的总和，N为总的级联模块数，其差值经过PI调节后可得到各相得有功调节量。

相内调节量如图10所示。

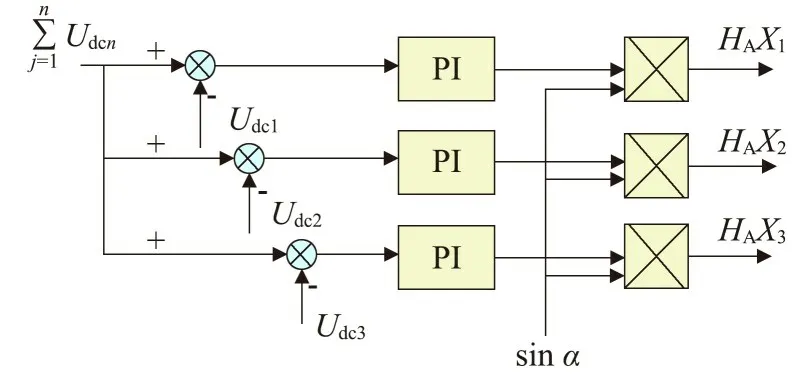
图10 相内均压控制

3.3 直接功率自适应控制

针对功率分解算法，采用一种改进的载波层叠调制策略［16］，该方法不仅具备载波相同层调制良好的消谐性能，还兼有载波移相调制开关分配均衡的特性。

首先对调制信号uz进行取整处理，得到调制信号整数部分uz1与小数部分uz2，再通过uz2与单路三角形载波信号um进行比较，得到脉冲信号p1，然后，将脉冲信号p1与uz1叠加，获得多电平脉冲信号p2，开关状态的定义在此不再赘述，最后将调制信号分配给H桥。

将所介绍的调制策略与直接功率控制［18-21］相结合，引入功率分解与自适应PI控制器，应用于级联混合补偿系统，级联系统控制如图11 所示，其中改进瞬时功率计算参考文献［4］。

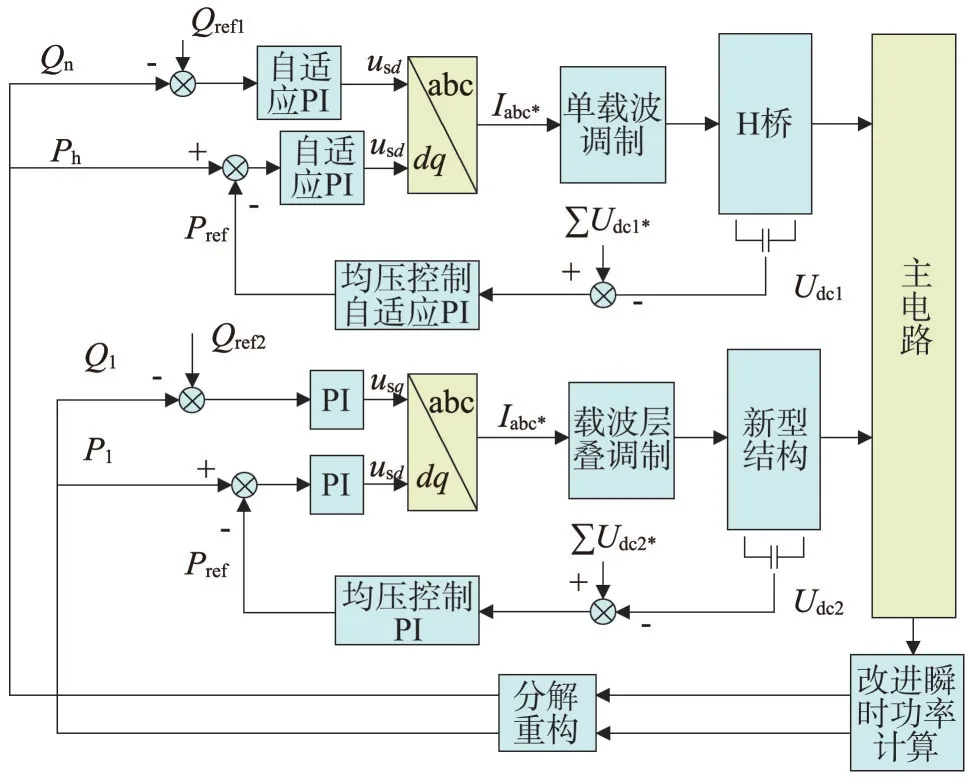
图11 级联系统控制

图11 中，Ph、Qh为对原始功率数据分解后的高频，Pl、Ql为对原始功率数据分解后的低频分量，Pref、Qref为系统指定的功率反馈值或参考值。

考虑到无功需求的不稳定性，功率分解后SVG部分接收到的指令信号均为高频功率信号，但从图8中可以看出，面对纯积分环节，固定PI控制器的响应速度并不理想，而响应速度等指标在补偿系统中尤为重要，因此，此处引入自适应PSO-PI 控制器。旨在提升系统的响应速度。

在变压器上采集瞬时功率数据，经过Mallat 算法，可将功率数据分解为多组高低频不同的数据，经判断后重构，分别分配给新型结构与SVG 控制部分输入模块，发出补偿电流，对系统进行补偿。

所述控制策略的目的是将需要补偿的无功功率进行分解，根据补偿设备性能的特征进行分配，在不损失动态性能的前提下，尽可能节约成本，提升系统的鲁棒性。

4 仿真验证

4.1 补偿效果

在验证所提变压器集成级联混合无功补偿系统及其控制策略的有效性上，基于Simulink 搭建了10 kV/380 V 系统仿真模型，变压器采用DYN11 接线，负载采用稳定阻感支路（R=0.3 Ω，L=0.1 H）作为恒定无功负载，0.2 s阻感支路（R=0.5 Ω，L=10 mH）作为低频变化负载，40 Hz 变化的阻感支路（R=0.1 Ω，L=0.01 H）作为高频变化负载，谐波源选用带阻感支路（R=15 Ω，L=0.1 H）的三相不控桥，变压器选用10 kV/380 V，容量为1 MVA；混合无功补偿系统接入点电压为3 kV，级联SVG直流侧电容指令值700 V。

负载侧谐波源波形如图12 所示，谐波源谐波含量如表2所示。

表2 谐波源谐波含量

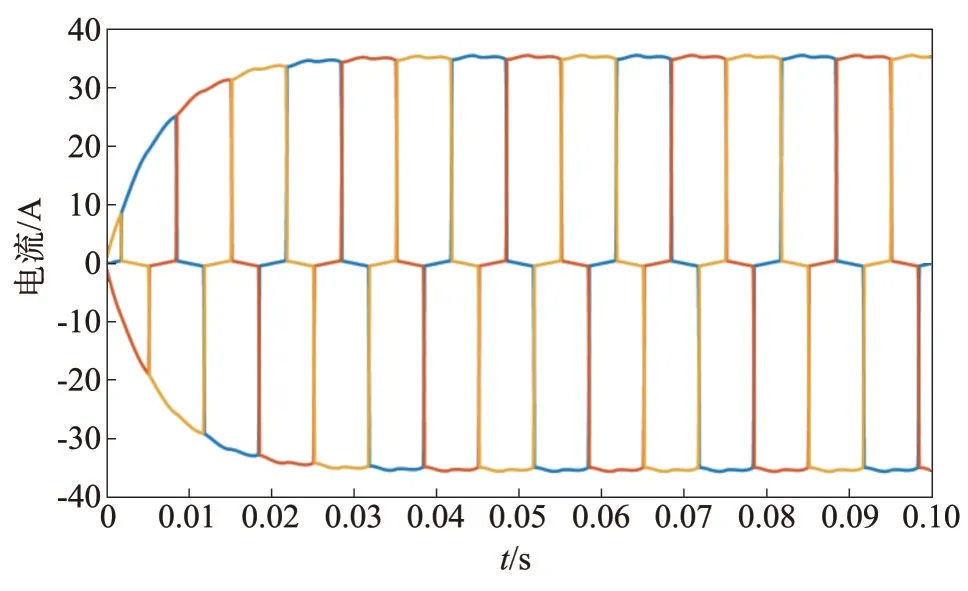
图12 负载谐波源波形

为验证该系统有效性，可通过电源侧补偿前后波形图，功率因数等数据进行对比，电源侧补偿前电压电流波形如图13所示。

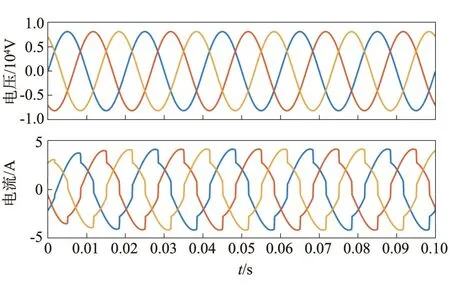
图13 电源侧补偿前电流电压波形

图13 中可看出，补偿前，电流畸变较为严重，补偿前电源侧电流谐波数据如表3所示。

表3 电源侧补偿前电流谐波

针对所提负载，采用新型结构与SVG 容量比为10：1 的混合无功补偿系统，补偿后电流电压波形如图14所示。

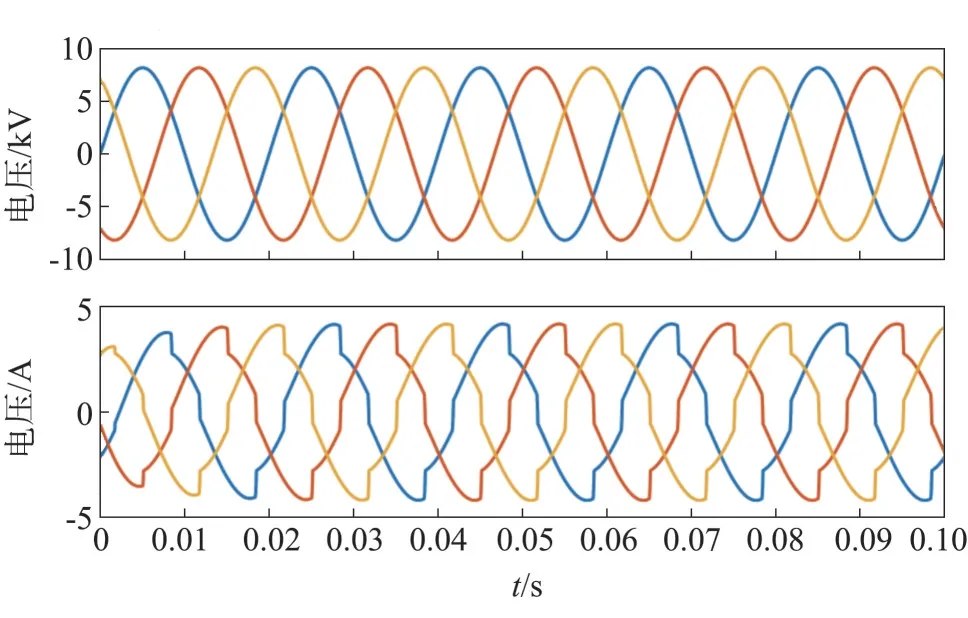
图14 电源侧补偿后电流电压波形

由图14 可看出，补偿效果较好，谐波数据如表4所示。

表4 电源侧补偿后电流谐波

补偿前后谐波畸变率（Total Harmonic Distortion，THD）及功率因数如表5所示。

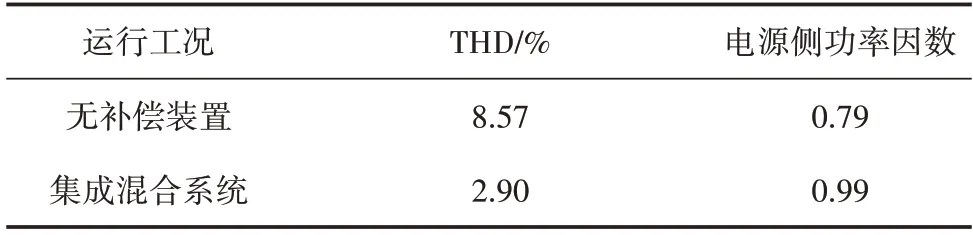
表5 补偿前后数据对比

4.2 PSO-PI控制器性能对比

为验证PSO-PI 控制器与传统PI 控制器的性能对比，选取SVG 直流侧A 相各电容电压之和的平均值作为参考量，如图15所示。

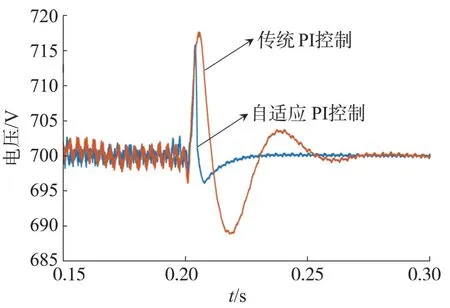
图15 PSO-PI控制器与传统PI控制器下直流侧电压

由图15可知，传统PI控制器的PI参数选择由传统经验值Kp=0.8，Ki=80，而PSO-PI 控制器对参数进行动态优化，从图中可以看出，在0.2 s 负载（0.5 Ω，1 mH）变化，PSO-PI 控制器控制的直流侧电容在超调量与响应时间等方面效果更好，传统PI 控制器经过约0.06 s 达到稳态值，而PSO-PI 控制器由粒子群算法（粒子群规模100）间歇更新PI 参数，只用了约0.03 s即达到稳态值，较传统PI控制器性能更为优越。

5 结语

针对变压器高压侧集中式无功补偿，初始投资较大，分散式补偿协调能力较差等问题，提出一种基于功率分解的变压器集成级联混合无功补偿装置，可利用新型结构补偿频率较低幅值较大的低频无功分量，SVG 对频率较高幅值较小的高频无功分量进行精确补偿，同时抑制电路中的谐波。

通过对真实变压器功率数据进行分解，证实功率分解在提高补偿系统经济性上具有可操作性。通过对变压器集成补偿系统进行仿真，验证了所提方案在无功补偿及谐波抑制上的有效性。成本问题一直困扰着生产实践，可通过对SVG 与新型结构输出补偿功率的分析，合理配置SVG 与新型结构容量。