冬奥单赛区公铁接驳疏散时刻表 协同优化研究
李祯怡,王洪业,颜 颖,王 京
(1.中国铁道科学研究院集团有限公司 电子计算技术研究所,北京 100081;2.中国国家铁路集团有限公司 客运部,北京 100844;3.中国铁路北京局集团有限公司 客运部,北京 100860)
0 引言
2022年北京冬奥会采用“两地三赛区”办赛模式,其交通运输系统主要由公路与铁路组成。面对奥运期间人群短时高强度疏散需求,2种运输方式间的运营协调是一项重要研究内容。目前,学者在城市公共交通场景中针对运营协调问题,主要从时间协调和组织协调等角度开展研究。
考虑到城市交通受路况等因素影响,常规公交到站可能存在延误,如Lee等[1]分析常规公交不同到达时间分布与客流密度关系,并从旅客角度建立换乘费用模型,优化常规公交停站松弛时间;张宇石等[2]对轨道交通与常规公交不同衔接方式的换乘特性分类分析,以系统总费用最小为目标,优化2类交通方式的发车间隔和公交停站松弛时间。Steven[3]、Vaughan[4]和Chang等[5]针对多点单线、环形、平行线路公交,建立企业运营费用和旅客换乘费用综合模型,从数值角度分析轨道线长度、轨道交通和公交发车间隔、停站间距与费用间的关系。上述研究更多从运输系统角度考虑运营协调问题,针对系统内部旅客分布特征研究较少。
基于单赛区冬奥旅客出行行为特征,研究单赛区的公铁运输接驳疏散系统时刻表协同优化,综合考虑2部分优化内容。在高速铁路运输层面,主要解决在运行径路、开行频次、列车编组和停站方案等确定的情况下与赛区公交接驳的列车始发时间优化;在赛区公交运营层面,主要解决在高峰和平峰协同环境下,赛区公交线路规划及时刻表优化。
1 问题描述
1.1 问题假设
对公交和高速铁路运行相关要素、客流分布特点做出以下假设。
(1)冬奥场馆间定制公交线路仅包括站站达线路和直达路线(各场馆与高速铁路站间往返);高速铁路列车采用一站直达开行。
(2)赛区内道路状态良好,公交车可以以恒定速度通过径路上任意区间。
(3)公交网络只考虑旅客无换乘出行;平峰时各场馆间旅客出行需求在单位时段内服从均匀分布;高峰时赛时场馆与接驳站间客流分布为高峰客流分布,其余各OD间的旅客出行需求与平峰时分布一致。
(4)高峰时段内场馆观赛客流分3阶段疏散。第1阶段,单位时间内的客流逐渐增大直至达到饱和疏散能力;第2阶段,以场馆饱和疏散能力稳定疏散客流;第3阶段,单位时间内的客流逐渐减少直至恢复平峰客流状态。
(5)考虑到冬奥疫情管理及观众乘坐高速铁路免票政策,观赛客流仅在观赛场馆与高速铁路接驳站间出行,且乘坐高速铁路离开赛区;其余人员仅在场馆间出行。
1.2 冬奥公铁运输网络与旅客出行描述
设V为冬奥期间某赛区场馆的公交站点(含高速铁路站)集合,|V|为场馆数量,个,站点v∈V,赛区内定制公交网络为GBus;赛区间高速铁路运输网络为GRail,沿线车站数|N|,个。2个运输网络共同构成公铁运输网络G=GBus∪GRail, 2个网络的接驳高速铁路站为slink∈V,网络运营时段为T=[T1,T2]。设公交网络GBus公交车集K包含2类公交:站站达公交集Kss、场馆与高速铁路站间直达公交集Kdir;高速铁路网络GRail仅包含高速铁路站始发列车集W。
对于公铁运输网络某一点对(r,s)∈RS,RS=V×V,设客流分布时段与公交运营时段范围一致。客流密度函数frs(t)根据场馆赛程设置,单位为人/h。 针对[t,t+ Δt)时段,如果为平峰时段,则frs(t)为常数;如果为高峰时段,则frs(t)为分段函数(由假设(4)可得)。
对于旅客在赛区公铁运输系统中的出行选择,如果旅客目的地不含高速铁路站slink,则旅客在系统中仅进行公交选择。如果旅客目的地为高速铁路站slink,平峰时期旅客以一定比例选乘高速铁路,高峰期观赛客流均选乘高速铁路(由假设(3)和假设(5)可得)。
冬奥赛区旅客出行径路以公铁运输网络为基础,旅客出行径路形成过程即是对公铁运输网络弧段的选择过程。对于不同时段内的到达客流,可以选择不同的乘车弧集。旅客通过换乘弧集将公交乘车弧集与高速铁路列车乘车弧集连接,构成旅客出行径路集。冬奥公铁运输网络及旅客出行径路如图1所示。

图1 冬奥公铁运输网络及旅客出行径路Fig.1 Bus-rail transportation network and passenger travel routes for Winter Olympics
1.3 冬奥公铁运输网络运营模式
设赛区内公交发车枢纽由多个公交场站组成。平峰时段,赛区主要从端点站对向开行ss(站站达)型公交。高峰时段,赛区内增开场馆至高速铁路站间dir (直达)型公交。公交车集为K,某趟公交k∈K,设其始发站为pk,类型为tyk,发车时间为dk,沿线经过m(k)站,个,则K= {k= (pk,tyk,dk) |pk∈V,tyk∈ {ss,dir},dk∈ [T1,T2]}。对于站站达公交集Kss,其始发站集为{p1,p|V|},p1和p|V|为端点站,始发时间集为D∈ [T1,T2];设p1始发为下行方向,用表示,p|V|始发为上行方向,用Kssp|V|表示。对于直达公交集Kdir,设始发站v∈V, 始发时间集D∈ [T1,T2],与站站达公交相同。设区间||v,v+1 ||运行时间tv,s;各公交车站最大停站时间为τBus,s。对某趟列车w,设其发车时间为dw。赛区公交k可以在接驳站点slink与其到达时间之后开行的所有高速铁路列车进行换乘。
1.4 冬奥公铁运输网络时刻表协同优化
基于公铁时空运输网络和旅客出行径路分析,冬奥公铁运输网络时刻表协同优化问题可以描述为:给定冬奥某赛区内旅客OD对的时变出行需求,公交及列车运行径路、停站方案,以及列车的开行数量,在公铁运输网络运营能力约束下,优化系统内公交开行数量和公交、高速铁路列车运营时刻表,使得旅客出行时间与企业运输成本综合值最小。
2 模型构建
2.1 目标函数构成
冬奥单赛区公铁运输接驳疏散系统协同优化是一个包含旅客出行时间与企业运输成本的多目标优化问题。定义旅客总出行时间为Tapllas,s。在列车开行数量一定条件下,系统内企业运输成本指公交运营成本(不考虑固定成本)。为保证多目标函数各部分尺度一致,将公交运输成本转化为公交运营总时间TBus,run,s,并引入调节参数α。综合优化目标可以描述如下。

式中:Tall为综合优化目标,s。
2.1.1 旅客出行时间
(1)单旅客出行时间。承接上述公交集定义,对于r场馆经停的站站达公交车集用Kssr,p1和Kssr,p|V|表示,直达公交车集用表示。设点对(r,s)的某旅客,乘坐公交kr,能力为Ckr,人;换乘高速铁路列车w,能力为Cw,人;(r,s)间距离定义为lrs,m;则公交kr在赛区内沿途经过m(kr)rs站,个。据前所述,该旅客出行时间包括公交在途时间、公交候车时间、列车换乘时间,单位均为s。该点对单个旅客出行时间表示如下。

其中,关于公交在途时间,对于点对(r,s)的旅客,如果目的地s=slink且旅客出行时间在r的散场高峰时段,旅客可选乘站站达或直达公交;如果s∈V slink,旅客仅选乘站站达公交。公交候车时间表示如下。

式中:τkr为停站时间,s。如果kr∈Kssr,p1,此时kr标号为kssr,p1;或kr∈Kssr,p|V|,此时kr标号为kssr,p|V|,此2种情况kr的停站时间τkr∈ [0,τBus]。如果则此时kr标号为
关于公交候车时间,对于在t时刻从r站至s站的旅客,设其乘坐第kr趟公交,公交到站时间为,离站时间为,则旅客在r站的公交候车时间如下。

求解公式 ⑷ 需要获得t时刻到达旅客与所乘公交kr的关系,以及第kr趟公交的对应离站时间。 公交通常会优先服务更早到站的旅客,即“先到先服务”。旅客会乘坐最近到站的目的地公交,即“先到先乘车”。定义第kr趟公交在r站的最早加载时间和最晚加载时间为,[6]。对于站站达公交,其最早加载时间等于前一趟站站达公交最晚加载时间;对于至高速铁路站的直达公交,其最早加载时间等于前一趟站站达公交和直达公交最晚加载时间中的最大值。定义和l为最近一次离开r的站站达和直达公交的最晚加载时间。则表示如下。
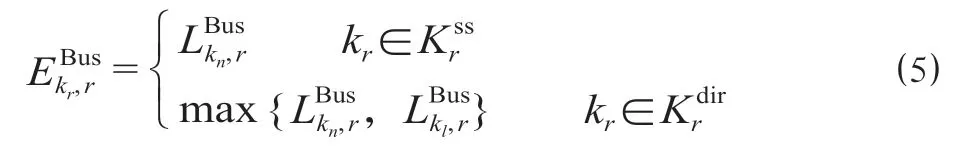
式中:Krss为经停车站r的站站达公交车集,Krdir为经停车站r的直达公交车集。
如果运载旅客超过公交定员,未加载旅客需等待后续车辆。设公交在车站r的离开时间为x,则表示如下。
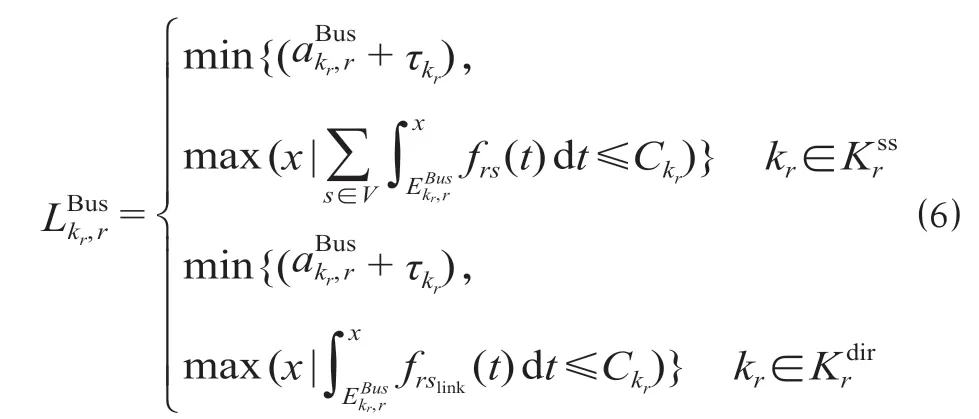
公交在沿途离站时间由客流加载状态决定。对车站r,如果规定停站时间内公交满载且,则;如果规定停站时间内公交满载且,则;如果达到最大停站时间后公交仍然未满载,则
关于列车换乘时间,设相邻列车w与(w-1)的图定始发时间为和,终点站到达时间为和,旅客到达slink时间为t'。则换乘至列车w的时间描述如下。

列车严格按照时刻表运行,因而实际始发时间与列车是否满载无关。设第w趟列车最早加载时间为,最晚加载时间为,第(w-1)趟列车最晚加载时间为。设列车在t'时间的客流密度函数为frs(t'),类比公交分析过程,则与表示如下。
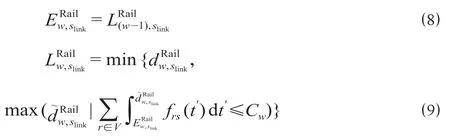
(2)旅客出行总时间。基于单个旅客各部分出行时间分析,旅客总出行时间表示如下。

(3)旅客到达强度分布。赛区旅客到达时段分为平峰和高峰时段,2种时段随赛程分布于整个运营时段[T1,T2],设车站r在[ti,ti+1)平峰时段客流密度为高峰时段为设[ti,ti+1)平峰时段的客流量为qrs(t),人,则frsU(t)为常数(假设3);高峰时段的客流密度frHs(t) (假设4)由3段函数构成。设r站客流最大疏散强度为Frmax,第1与第3阶段拐点分别为tiθ和tiξ,frs(t)为线性变化,则第1阶段为[ti,tiθ),设此时客流强度以固定比率θ随时间t递增,,b为平峰条件下客流量基数;第2阶段为[tiθ,tiξ],设此时客流强度恒定为Frmax,frHs(t) =Frmax;第3阶段为(tiξ,ti+1],设此时客流强度以固定比率ξ随时间t递减,ξt+b',b'为平峰条件下客流量基数。
2.1.2 公交运行总成本
设公交k始发站为,终到站为,用标识始发站为的公交,则其经过站数为m(),个;停站时间表示为τkp∧k,s。此时,r为始发站∧,则其运行总时间为TBus,run表示如下。
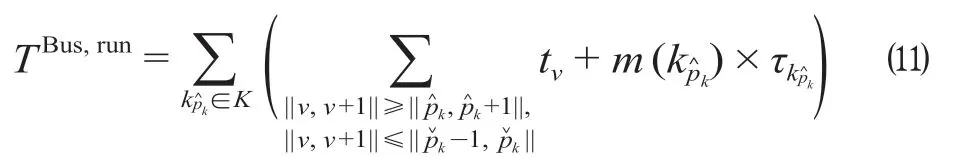
综上,目标函数表示如下。
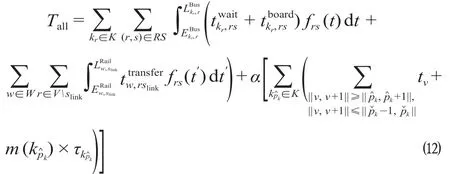
2.2 约束条件
根据研究设计,如果公交车始发时间、始发站和类型确定,即可确定公交运行方案;由于高速铁路列车开行对数和径路确定,仅需要确定高速铁路列车的始发时间即可确定时刻表。
(1)始发终到时间约束。任一公交或高速铁路列车的始发终到时间均需要满足运营时间限制。则公交与高速铁路列车的始发终到时间约束表示如下。
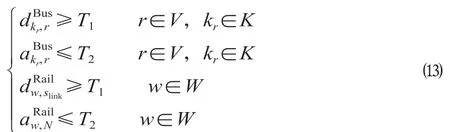
(2)发车间隔时间约束。相邻2趟高速铁路列车运营需要满足最小和最大发车间隔时间约束,以满足安全追踪间隔和服务水平。设列车最小发车间隔为Hmin,Rail,s,最大发车间隔为Hmax,Rail,s;设公交最小发车间隔时间为Hmin,Bus,最大发车间隔时间为Hmax,Bus,s。则发车间隔时间约束如下。
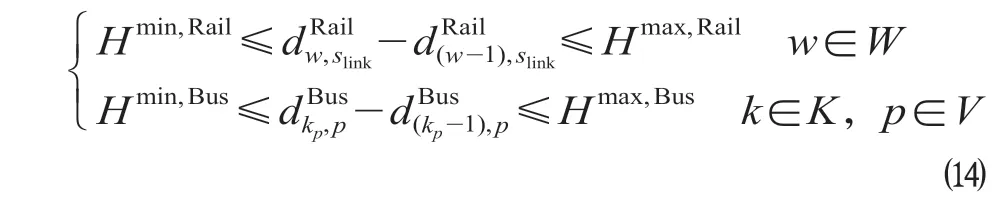
(3)客流需求约束。公交车、高速铁路列车需要在空间上满足赛区客流出行。设赛区内点对(r,s)的旅客出行需求量为Qrs,人;点对(r,slink)的高速铁路站旅客需求量为,人。则客流需求约束如下。
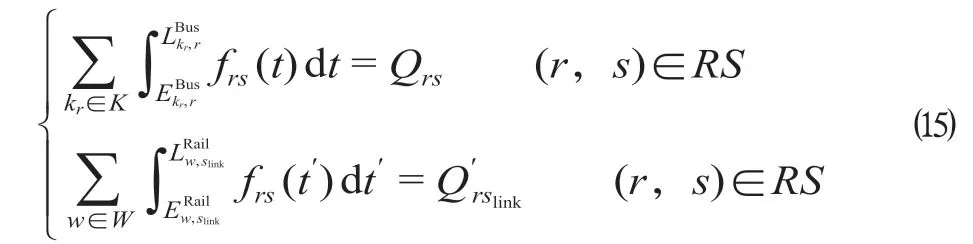
(4)公交车与高速铁路列车定员约束。对于当前加载的公交站u,加载人数与车上剩余人数之和应小于或等于最大运输能力。则公交车与高速铁路列车定员约束如下。
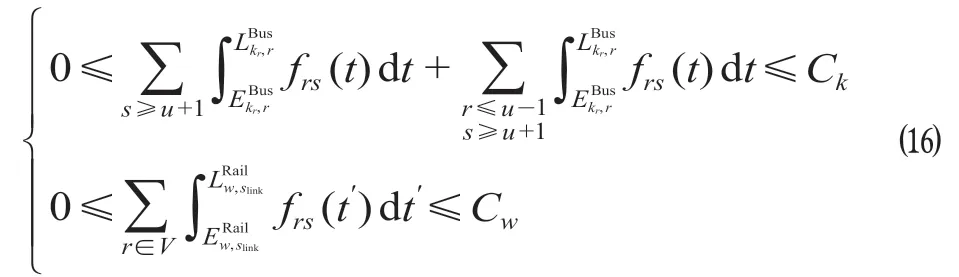
(5)公交车辆周转约束。为满足赛区公交周转,站站达公交上下行车辆数对应相等,设反向直达公交通过空跑实现车辆周转。则公交车辆周转约束如下。

式中:N U为站站达公交上行车辆数,辆;N D站站达公交下行车辆数,辆。
3 模拟退火算法关键技术
公铁接驳疏散系统时刻表优化为NP难问题,可以采用智能算法求解[7]。考虑到模拟退火算法鲁棒性较好且概率全局最优收敛[8],因而将其作为求解算法。求解过程分2个阶段进行,每次求解过程中先对赛区公交运营方案进行求解,后进行高速铁路列车时刻表规划。
3.1 初始解构造
系统内初始运营公交构造为站站达类型,公交与列车均匀发车。假定赛区内上行方向旅客总量为;下行方向旅客总量为;高速铁路站到达客流总量为,人。赛区内上行公交的运营数量,上行公交发车间隔为,s;下行运营数量,下行公交发车间隔为,s。列车运营数量为NRail,辆;发车间隔为
根据运营方案对赛区内客流进行分配,初始解目标函数值的算法设计如下。
步骤1:输入客流分配的相关参数。输入赛区旅客客流量及客流分布,公交和高速铁路运营时间[T1,T2],赛区内场馆集合V,区间||v,v+1 ||的运行时间tv,停站时间τBus;公交最小发车间隔时间Hmin,Bus,最大发车间隔时间Hmax,Bus,公交运载客流上限值Ckp;列车最小发车间隔时间Hmin,Rail,最大发车间隔时间Hmax,Rail,高速铁路列车运载客流上限值Cw。
步骤2:计算目标函数值。公交加载:遍历构造的初始公交集、径路和停站,计算公交kp到达沿途停站r时的剩余能力;剩余能力大于0,则基于先到先服务原则加载客流,直至达到停站时间τBus,或达到公交运载能力上限值Ckp时停止加载;计算乘坐公交kp的r站旅客候车时间和在途时间,公交kp的全程运行时间,记录开始加载时间和停止加载时间(公交从r站离站时间),更新此时r站剩余客流。高速铁路列车旅客加载:按照旅客到达顺序加载,直至达到列车始发时间或列车定员Cw时停止加载;计算乘坐列车w的旅客换乘时间,更新此时高速铁路站剩余客流。
步骤3:计算初始目标函数值。当场馆公交和列车剩余能力为0或剩余加载客流为0,计算初始目标函数值。
3.2 邻域解搜索策略
邻域解构造是模拟退火算法求解的关键问题[9]。 根据文献[8]的构造方法,结合问题求解特征,设计邻域解搜索策略,主要包括停开、增开公交,调整公交、列车始发时间。
策略1:停开公交。从客座率小于下限约束的公交集合中分上下行随机各删除1趟公交。
策略2:增开公交。选择旅客总等候时间最长的时段,在满足开行约束条件下分上下行各增开1趟公交。如果时段内客流主要前往高速铁路站,则增开1对直达公交。
策略3:调整公交始发时间。随机选择1趟上行公交kp,其始发时间在时间范围内随机调整。
策略4:调整列车始发时间。随机选择1趟列车w,在满足开行约束条件下将始发时间以给定概率向客流密集时段移动,否则始发时间在时间范围内随机调整。
4 案例分析
4.1 研究数据
崇礼赛区包括国家跳台滑雪中心、国家越野滑雪中心、国家冬季两项中心和云顶滑雪公园4个主要场馆。京张高速铁路(北京北—张家口)作为北京和崇礼赛区间的重要交通运输通道,承担冬奥2个赛区间的部分客流。太子城站为崇礼赛区的端点高速铁路站,与赛区内其他场馆客流交互密切。
崇礼赛区4个场馆与太子城站的位置组合呈L型分布;相邻两地间最远约4.1 km,最近约0.6 km; 参考赛区既有道路设施情况,相邻站点间均有道路可以相互通达。因此,赛区场馆间及高速铁路车站间满足开设公交的距离、设施等条件,可以设置相应公交站点。崇礼赛区冬奥场馆专线公交站点如图2所示。
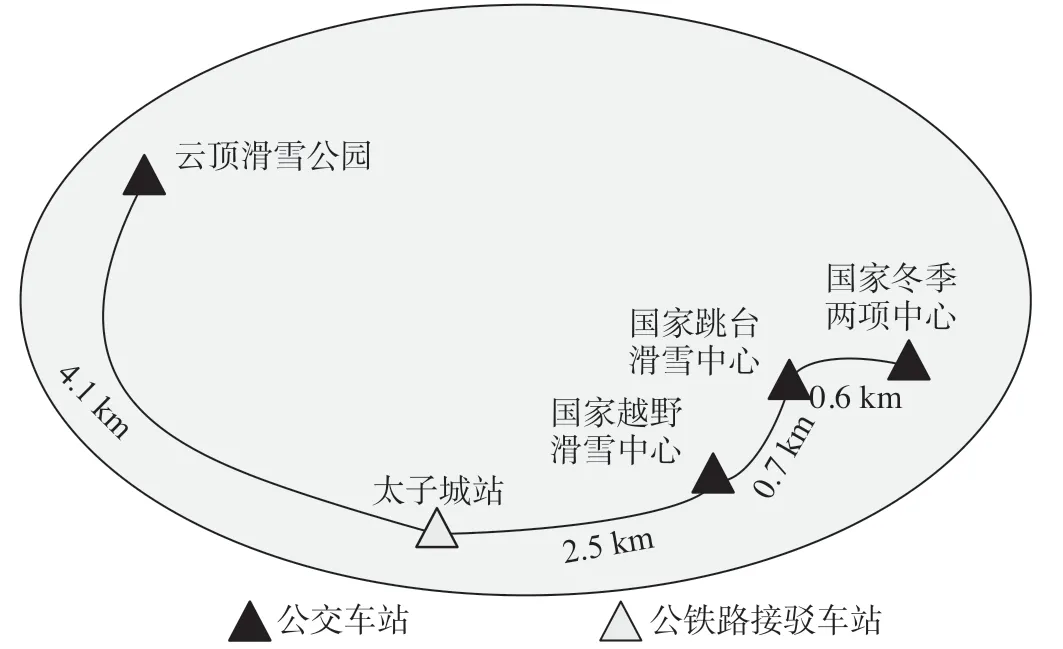
图2 崇礼赛区冬奥场馆专线公交站点Fig.2 Bus stop map of special line for Winter Olympic venues in Chongli competition area
考虑疫情影响,赛区场馆观赛人数按50%上座率预估[10]。选择2022年2月12日为分析日期,预估当日赛事时间及观赛人数。崇礼赛区场馆观赛人数预估如表1所示[11]。
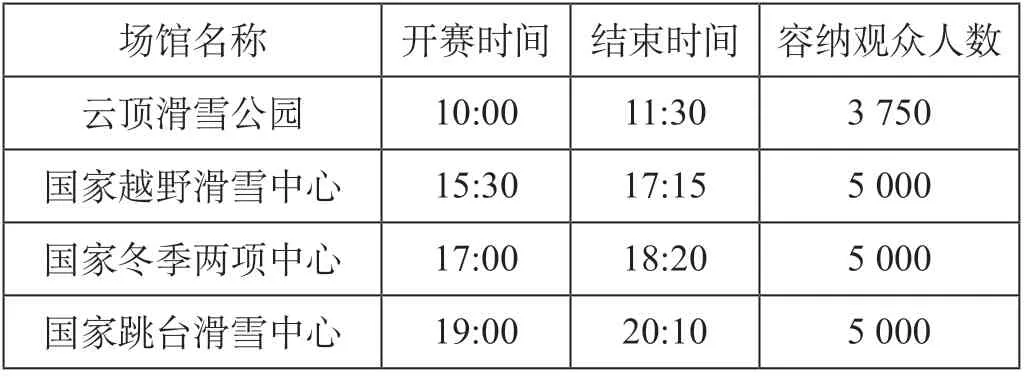
表1 崇礼赛区场馆观赛人数预估 人Tab.1 Estimated number of spectators at venues of Chongli competition area
赛事结束后的一段时间内,场馆疏散客流满足高峰期客流分布。设高峰期客流强度递增比率θ= 8人/min,Frmax= 80人/min。令平峰期各OD间客流交互强度相同且在小时内服从均匀分布,各OD间的客流强度为frsU(t) = 2人/min。其中,小时客流总量根据历史均值确定。设赛区运营时段为[6 : 00,23 : 00],赛区内单日不含高速铁路站的OD客流总量为3 072人,含高速铁路站的OD客流总量为 22 590人。
公交和高速铁路数据主要包括定员、径路和停站。公交定员Ck= 60人,站站达公交径路端点站为云顶滑雪公园和国家冬季两项中心,停站模式为站站停;直达公交端点站为赛区场馆站和太子城站,仅在端点站停靠。列车席位定员Cw= 1 200人,开行直达列车25趟,开行径路为太子城—北京北。
4.2 计算结果
运用上述模型和算法,求解得到崇礼赛区公铁运营时刻表如图3所示。图3分为上下2个部分:上部为太子城站始发列车运营时刻示意图,下部为赛区接驳公交运营方案图(火车站至场馆间折返空跑直达公交未在图中画出)。图中公交运行线较密集区域是由于客流高峰期大量直达公交开行所致;客流平峰期,站站达公交的开行具备一定周期性。

图3 崇礼赛区公铁运营时刻表Fig.3 Bus-rail operation timetable of Chongli competition area
优化后的公铁运输接驳疏散系统运营评价指标如表2所示。满意解所对应的旅客公交平均候车时间与高速铁路列车平均候车时间均在10 min左右。下行公交客座率较高,主要因场馆客流分布不均所致。高峰期旅客公交平均候车时间为12.2 min,平峰期旅客公交平均候车时间为10.8 min;高峰期旅客列车平均候车时间8.7 min,平峰期旅客列车平均候车时间36.5 min。高峰期与平峰期旅客公交候车时间分布较为均衡,平峰期旅客列车候车时间亦在可接受范围内。该模型与算法的最终迭代解既保证了旅客服务水平,也保持了一定的运营效率。

表2 公铁运输接驳疏散系统运营评价指标Tab.2 Operation evaluation index of bus-rail transportation connection evacuation system
基于计算结果,统计分析赛区运营时段内公交开行特征。公交时段开行趟数及客座率分布如图4所示。站站达公交时段分布较为均匀,直达公交时段分布随赛事日程变化较大。2类公交高峰时段客座率较高,直达公交客座率均值超过90%,站站达公交客座率均值约40%。
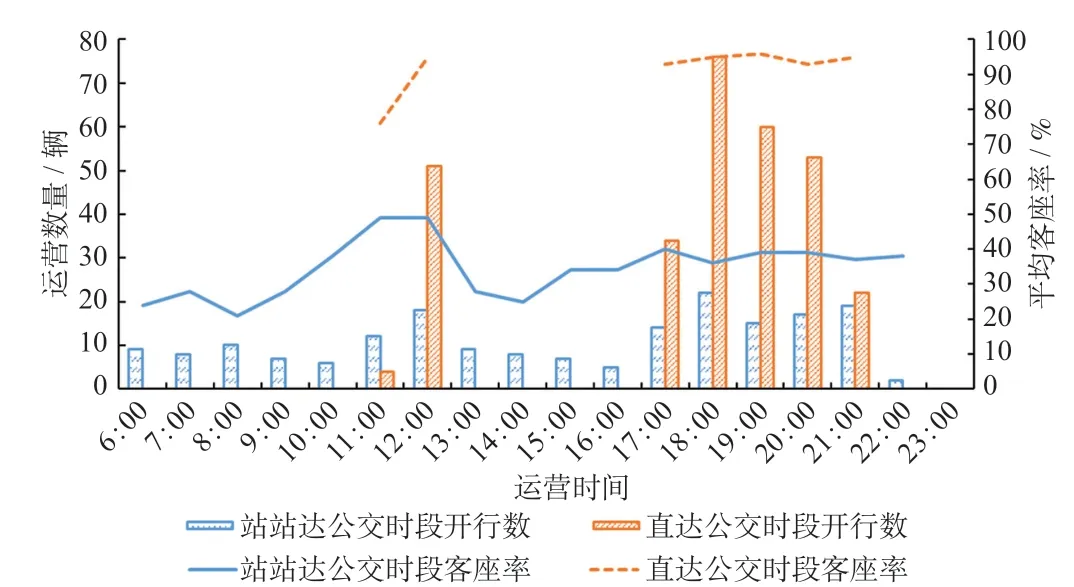
图4 公交时段开行趟数及客座率分布图Fig.4 Distribution of bus hourly operation number and passenger seating rate
算法迭代收敛趋势如图5所示。当迭代次数为1 000代时即收敛,表明算法具有较高的运行效率,且收敛趋势较为稳定,有良好的鲁棒性。

图5 迭代收敛趋势Fig.5 Iterative convergence trend
5 结束语
考虑平峰和高峰2类客流特征,建立客流模型定量描述单赛区客流疏散过程。根据冬奥赛区多种交通方式接驳特点,设计赛区内公交及高速铁路列车的接驳运输模式,构建单赛区内客流的公铁疏散系统。基于赛区内客流出行时变OD的模拟需求,在高速铁路列车运力配置、高速铁路列车与公交定员等约束条件下,建立面向旅客服务水平和企业运营成本的公铁疏散系统时刻表优化模型并求解优化。所设计的初始解生成构造和邻域解搜索策略,能较好地适应模拟退火算法求解。求解方案可以较好地满足旅客疏散需求,旅客平均候车时间相对较短且较为均衡。未来可以将公交车辆和高速铁路列车的交路设置加入模型联合优化,进一步提升接驳疏散方案的实际应用价值。

