基于模糊RPN的塞拉门驱动传动系统危害性分析

0 引言

塞拉门作为列车运营中最繁忙的系统之一，其主要由驱动传动系统、承载导向装置、锁闭装置、内外操作装置、电动控制装置以及基础部件等子系统构成

。驱动传动系统作为塞拉门的重要组成部分，因其工作频繁、强度高，将导致驱动传动系统的故障率明显提高。近年来，国内外很多学者利用故障树分析法，故障模式、影响及危害性分析法(Failure Modes, Effects and Criticality Analysis，FMECA)等可靠性理论、方法对塞拉门的可靠性和安全性进行了研究。刘萍等人采用重要度分析算法对故障树进行了定量分析，得到了车门的可靠性指标

。牟颖运用FMECA对塞拉门的关键部件进行可靠性分析，对关键部件的故障模式进行了综合性危害评估

。段毅刚等人将模糊数学理论与故障树方法相结合，得到了影响CHR5型动车组塞拉门系统的薄弱环节

。霍壮志等人运用模糊故障树并引入专家评估系统，对城轨车辆客室塞拉门系统进行了可靠性分析

。综上，针对塞拉门驱动传动系统的相关研究的文献和资料相对来说很少。本文利用模糊RPN(Risk Priority Number, RPN)方法分析塞拉门驱动传动系统的危害性，评价各类故障对系统产生的危害程度，为该系统的故障检测和诊断提供参考。

DOU Hong-wei, WANG Guo-wei, CHEN Liang, LI Pan, KAN Tong, QIN Yong-wen

心房颤动(房颤)是心力衰竭、快速性心室心率失常及痴呆等疾病的独立危险因素，与心房结构及电活动重构关系密切，而心血管不良功能状态是促进心房结构改变的重要原因[1-3]。胃饥饿素是一种具有多种生物活性的短肽，在多种心脏疾病的发生发展中起重要作用，但与房颤的关系并不明确[4]。本研究旨在探讨琥珀酸美托洛尔缓释片治疗房颤的效果及对血清胃饥饿素表达的影响。现报道如下。

1 模糊RPN方法[6]

传统的RPN是危害性分析(Criticality Analysis，CA)的一种分析方法，其本质是根据故障诊断和可靠性分析的经验依照故障模式评定等级标准对故障模式的发生频度等级(Occurrence,O)、严酷度等级(Severity,S)和检测难易程度等级(Detection,D)给出一个确切的数值，三者的乘积可计算出RPN值，显而易见以上过程存在着模糊性和不确定性。因此，为了降低评定等级过程中的模糊性和不确定性，可利用模糊语言变量和模糊综合评判建立模糊RPN方法。

1.1 模糊语言变量和模糊矩阵

1.1.1 模糊语言变量的表征

1.2.1 因素集的确定

传统的RPN根据自然语言表示的评定准则进行故障模式的危害性等级评定，即分析人员根据具体的故障模式和该评定准则，给出一个确切的数值。而模糊语言变量是将自然语言划分为五个等级，并分别用相应的模糊数表示这五个等级。在塞拉门故障诊断和可靠性分析领域中，模糊语言变量的等级及表征如图1所示，其相对应的自然语言等级见表1所示。

在图1(a)中，并结合表1的自然语言等级，某一故障模式发生频度被评定为4～8，模糊化为图中虚线三角形，该区间的中值(本例为6)对“发生频度中等”的隶属程度即隶属度为1，即当给出一个数值区间时，其中值具有最大的可能性，其他数值的可能性依次从中值向两侧递减，其可能性的变化用隶属度0～1表征。该模糊数表达了发生频度数值的模糊信息，模糊数与各语言变量的交点构成了一个模糊序集合

，由图1(a)中的虚线三角形区域可知，式(1-1)即为它的模糊序集合。

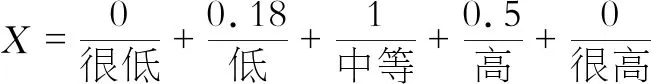
(1-1)

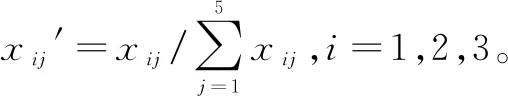
1

1

2 模糊矩阵的确定

病虫害是所有果树生长的天敌，我们要尽量早发现，及时采取措施，达到防治的效果。一般来说，种植者可以采取生物、药剂和物理三种方法结合防治苹果栽培过程中出现的病虫害现象，比如果园中可以悬挂杀虫灯，尽量用生物防治代替农药防治，并严格杜绝使用禁用农药。同时用相应的管理方法为草蛉和瓢虫创造良好的繁殖条件，加强生物防治。

大课之后，进行个人情况一对一分析，根据个人特点，分配不同的工种，然后到家道家政职业技术培训学校进行专业化学习与考核，通过精准对口，量身定制，大大增加了培训就业率，提高了员工的收入。

在分析某一故障模式时，要对发生频度、严酷度和检测难易程度三个因素进行模糊化处理，即将三个因素的模糊序集合构建成一个模糊矩阵，并对每一行进行归一化处理：

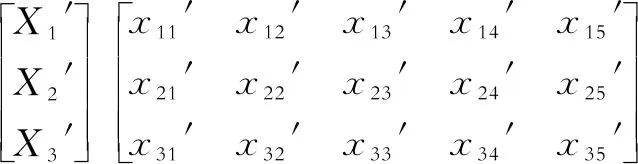
(1-2)

式(1-1)表达了故障模式发生频度数值的可能性分布。严酷度和检测难易程度的分析作上述同样的处理。

1.2 因素集和因素权重向量

随着西宁城市建设的发展，各种土木建筑的兴起，使得南川河河道两岸成为民生工程的重点区域，包括麒麟湾公园、中心广场、西门体育馆等公共场所。为此，河道的治理也需紧跟绿色发展步伐，进行大面积的绿化处理。研究区选取南川河谢家寨村段，河道长度约为1 490 m。

虽善意取得制度是对 “任何人不得转让大于自己权利的权利”法律公理的突破，但也不能理所应当的认为突破该原则就是继受取得。通说认为，善意取得之正当性是因为善意取得制度保护交易安全，因此，确有突破此原则之必要。若认为从无权处分人处取得物权，不仅是对该公理的侵犯，也是对善意取得制度正当性的误解。

与研究对象的危害性分析相关的三个因素构成了因素集合，不同元素表示危害性分析不同的评价项目。因素集通常用

表示：

={

,

,

}

(1-3)

式(1-3)中

表示第

个因素，即表1中的三个评价项目：发生频度、严酷度和检测难易程度。

(2)因素权重向量

由于各因素对系统危害性影响程度不同，因此定义一个因素权重向量来衡量各因素的重要程度。一般情况下，采用层次分析法确定因素权重向量。

={

,

,

}

(1-4)

式(1-4)中，

,

,

分别表示发生频度、严酷度和检测难易程度的权重值，三者之和为1。

1.3 评价集和单因素模糊评判矩阵

1.3.1 评价集的确定

通过抓取主流招聘网站的招聘信息，以海量数据为基础开展，设计紧缺度指标进行研究。传统研究方法一般采用问卷调查、企业访谈的方式。相比于传统方法，基于大数据的研究方法能够解决传统方法的数据获取难、数据质量差的痛点。采用大数据的方法使用计算机程序实现自动数据采集，获取的数据量巨大，而且数据多是现实中企业的真实需求，可信度高。

系统危害性分析结果的评定，也可用五级语言变量来表征。

={

,

,

,

,

}

(1-5)

式(1-5)中，

表示危害性等级，

,

,

,

,

分别表示很低，低，中等，高，很高。

1

3

2 单因素模糊评判矩阵

④环境管理:根据血站业务工作的具体流程,合理进行布局、分区。分为采血区和非采血区、清洁区和污染区,均需要隔离开来。确保采供血工作有条不紊的进行。加强环境管理,为患者提供安全、舒适的献血环境。由专人负责引导工作,指导献血者有序的进行检验和采血。采血环境应保持整洁卫生,并严格进行消毒,预防血液污染,并对报废血和受到污染的血液进行妥善处理,确保血液质量,采供血过程信息完整的记录在档案当中。

(1-6)

式(1-6)中，

表示第

个因素的单因素模糊评判矩阵，

表示只考虑第

个因素中第

个语言变量对评价集中第

个元素的隶属度。

1.4 危害性评判模型

1.4.1 综合评判矩阵

定义单因素模糊综合评判矩阵B：

=(

,

,

)

(1-7)

式(1-7)中：

(1-8)

定义综合评判矩阵

：

=

·

= (

,

,

,

,

)

(1-9)

1

4

2 危害性等级

故障模式的危害性等级可采用加权平均原则确定，适当选择权值对式(1-9)中的隶属度进行加权计算，即权重集

：

={

,

,

,

,

}

(1-10)

第

个故障模式的危害性等级评判序数：

周泽赡擦擦眼泪，接起了电话。周泽赡勉强笑着搭话，讲完电话后，门铃响了。周泽赡去开门，是白婗棠，他怀里抱着一只小鸡，看来有三四周大的样子，比周泽赡之前养的那几只都要大。

(1-11)

按式(1-11)计算出各故障模式的

值，并按照大小排序即可得到各故障模式的危害性等级。

2 塞拉门驱动传动系统的危害性分析

2.1 塞拉门驱动传动系统的FMEA分析

根据以上分析过程，统计10个故障模式的每个因素不同语言变量对评价集不同元素的隶属度，得到单因素模糊评判矩阵

，

，

：

2.3 基于模糊RPN的危害性分析

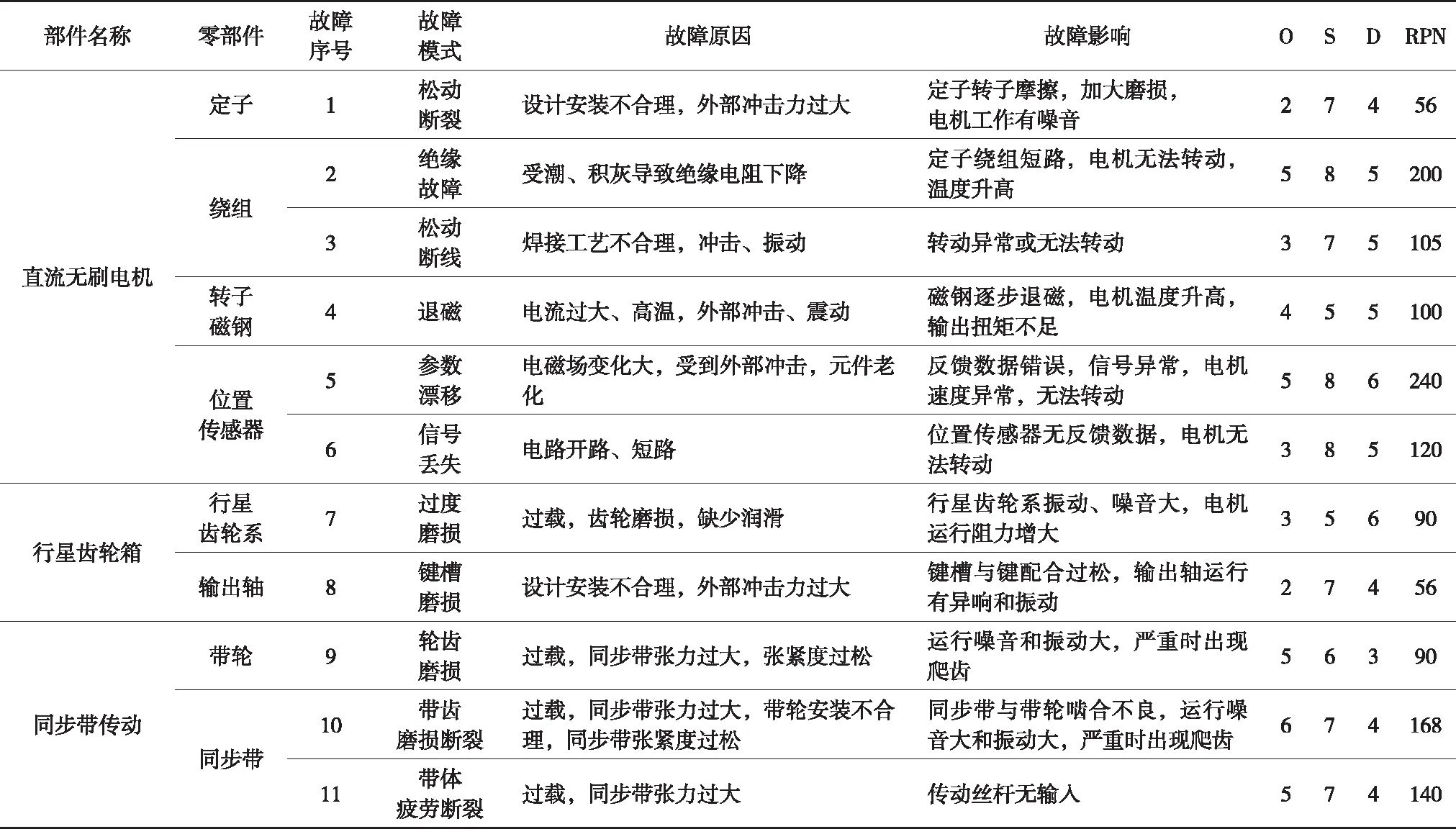
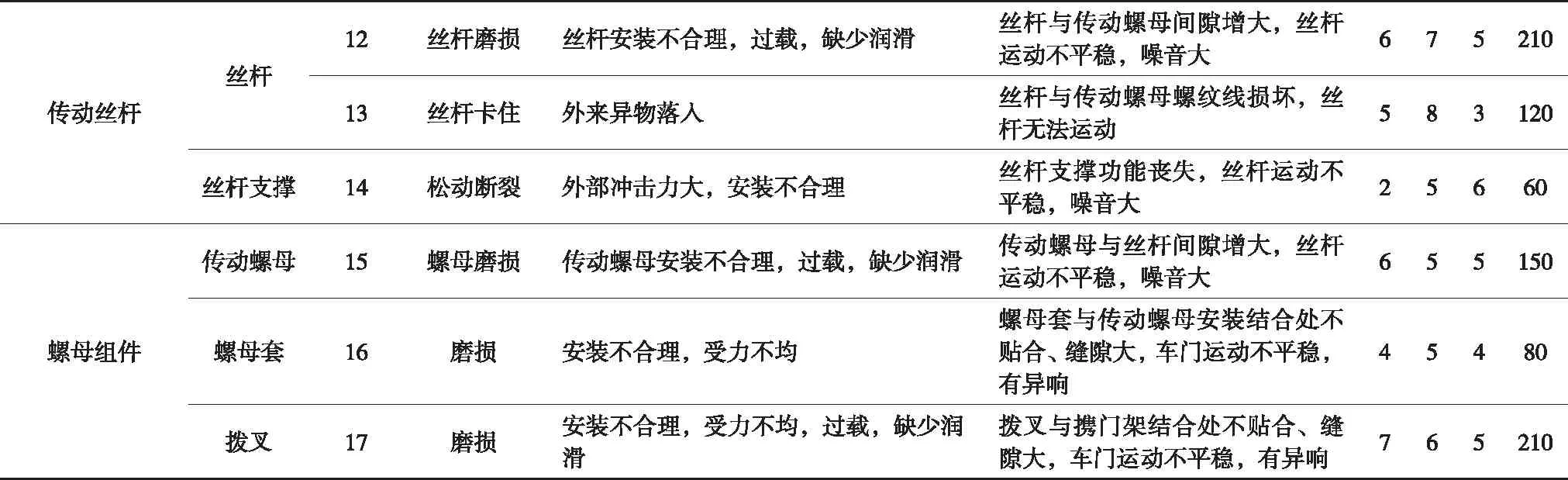
上述表2中列出了塞拉门驱动传动系统FMEA分析的详细结果，由于文章篇幅的限制，本文只选取RPN值大于100的故障模式进行危害性分析，即故障序号为2,3,5,6,10,11,12,13,15,17。

2.3.1 相关集合和矩阵的确定

(1)模糊矩阵 ，其中m表示故障模式的序号，即上述表2中的第三列。

结合表2中故障模式的发生频度等级、严酷度等级和检测难易程度等级的数值，对所分析的每个故障模式的三个数值进行模糊化处理，并进行归一化处理即可得到各故障模式的模糊矩阵，如表3所示。

1

2

2 因素权重向量的确定

通过走访、调研一线塞拉门维保、故障检修工程专家和可靠性分析领域的学者，并采用层次分析法确定因素权重向量

=(0

24，0

55，0

21)。

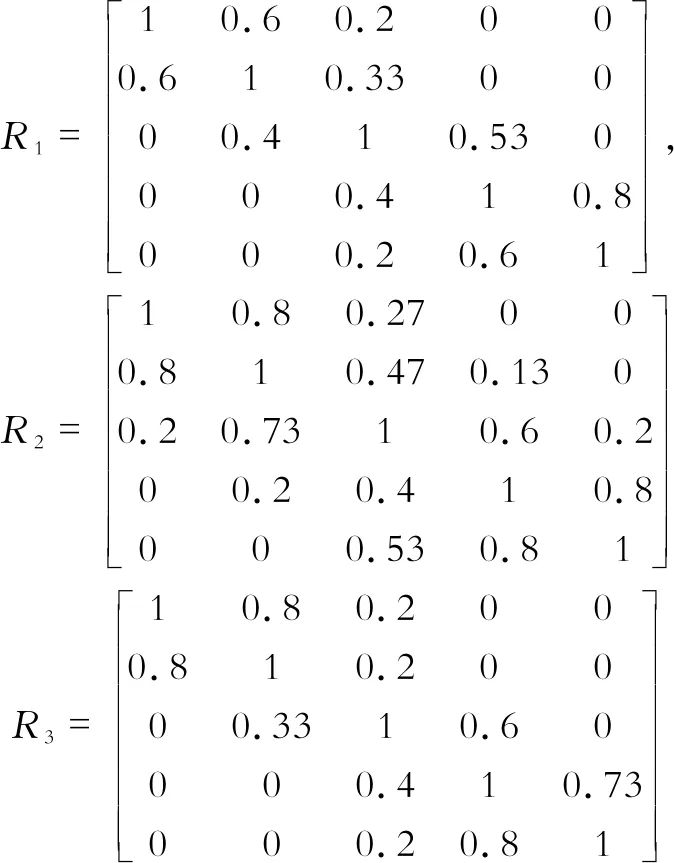
(3)单因素模糊评判矩阵

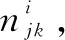
因素集

中每一个因素的每一级语言变量对评价集

的每一级语言变量的隶属度可构成单因素模糊评判矩阵，即

FMEA分析是危害性分析CA的基础。因此，利用模糊RPN方法对塞拉门驱动传动系统进行危害性分析之前，要先对其进行FMEA分析。塞拉门驱动传动系统由直流无刷电机、行星齿轮箱、同步带传动、传动丝杆、螺母组件等部件组成，使用FMEA分析方法对系统各部件可能发生的故障模式进行识别、归纳。结合表1的评定等级标准划分表，通过参照相关文献和查阅大量维修实例与相关数据

，对各故障模式造成系统正常运行的影响程度进行定级、取值，表2为塞拉门驱动传动系统的FMEA分析详细结果。

(2-1)

2

3

2 危害性CA分析

从表3中取故障模式2的模糊矩阵，如式(2-2)所示。将式(2-1)、式(2-2)代入式(1-7)、式(1-8)和式(1-9)可得到故障模式2的综合评判矩阵D

=(0.1107,0.3217,0.5785,0.6798,0.5044)。

(2-2)

同理可得其他故障模式的综合评判矩阵：

=(0

2081,0

4467,0

5609,0

5982,0

4063)，

=(0

0828,0

2855,0

5831,0

7162,0

5328)

其中, 最优化权dr={0.05, 0.45, 0.45, 0.05}, 是一种6阶线性中心格式; 整数q=4, 正常数Cq=103, 且ε=1/ χ=10-8. 关于WENO方法以及计算β3,r, β3,ave, τ6的细节, 可参见文献[15,17].

=(0

1898,0

3761,0

5200,0

6131,0

4833)，

=(0

1425,0

3753,0

5958,0

6786,0

4537)

=(0

1720,0

4231,0

5903,0

6310,0

4170)，

一位成功的画家必具两个基本品质：认真地面对客观世界，在观察、分析中丰富自己的人生体验，汲取创作的灵感；善于审视和寻找自我，不断从自我的体悟中发掘自己的才智与潜能，找到自身在艺术中的位置。对艺术家来说，表现客观世界和表现自我，应该是合二为一、互为表里的。从表面上看，画家画的是客观对象，实际上是在画自己，是在呈现自己的主观世界。

=(0

0995,0

3444,0

6249,0

7126,0

4641)

=(0

1888,0

3699,0

5209,0

6244,0

4940)，

=(0

2067,0

5399,0

7302,0

5858,0

2551)

=(0

1077,0

3808,0

6530,0

7163,0

4385)

选取危害性等级加权矩阵

=(1,3,5,7,9)，根据式(1-11)可计算出各故障模式的危害性等级评判序数：

= 6

04，

= 5

49，

=6

21，

= 5

76，

= 5

82，

= 5

62，

=5

98，

=5

79，

= 5

12，

= 5

87。按照危害性等级评判序数的大小排列的故障模式顺序为5,2,12,17,10,13,6,11,3,15。

总而言之，当前在面向现代柔性工业机器人的高精度控制方法中，基于运动学模型的评估和补偿方式是较为简单且技术成熟的一种，但是其仍旧存在一些问题，如模型的不定性、机器人在工作环境中不能够对某些防伪进行有效的补偿。而实现对外部测量设备的精度提高方式则能够有效的发挥工业机器人当前的设计制造特性，按照机器人的制造的设计原理对其定位误差的分布规律等进行摸索排查。因而说在实现工业机器人的高精度控制方法要求能够综合展开上述三种方式的协调统一，避免出现某一技术方式短板所带来的精度不精准的问题。

3 结论

(1)通过对塞拉门驱动传动系统进行故障模式与影响分析，并根据故障模式评定等级标准，得到了塞拉门驱动传动系统的FMEA分析结果。

4.3 根据多年观察节瘟发生也较重，在防治叶瘟和穗颈瘟时应对稻株所有节部亦应喷到药。不论叶瘟、穗颈瘟还是节瘟，均应做到及早防，及时治，并应做到喷得均匀、周到，方能起到防治作用。

(2)针对传统RPN的不确定性和模糊性，利用模糊RPN方法对系统进行危害性分析，根据危害性等级评判序数顺序可知，直流无刷电机的危害性等级最高，其次是传动丝杆，再次是同步带传动，最后是螺母组件。为此，在制订塞拉门驱动传动系统的维保策略、方案和计划时要重点关注直流无刷电机、传动丝杆、同步带和螺母组件，同时危害性分析结果也为塞拉门的可靠性分析提供了重要参考。

[1]刘晶.改进模糊Petri网在城轨列车客室车门系统故障诊断中的应用研究[D].北京交通大学,2014.

[2]刘萍,程晓卿,秦勇,张媛,邢宗义.基于模糊故障树的塞拉门系统可靠性分析[J].中南大学学报(自然科学版),2013,44(S1):310-314.

[3]牟颖. 地铁列车车门故障诊断与可靠性分析[D].大连交通大学,2018.

[4]段毅刚,齐金平.基于模糊故障树的动车组塞拉门系统可靠性分析[J].模糊系统与数学,2019,33(05):166-174.

[5]霍壮志,王云霞,曹芳芳,刘润波.基于模糊故障树的城轨列车客室塞拉门的可靠性分析[J].南京工程学院学报(自然科学版),2019,17(02):48-54.

[6]陈颖, 康锐. FMECA技术及其应用[M]. 国防工业出版社, 2014.

[7]吴飞翔. 城轨车门系统中无刷直流电机退化试验的研究[D].东南大学,2019.