某盘式制动系统热-结构耦合分析及结构优化

0 引言

制动器摩擦片与制动盘之间的摩擦系数对盘式制动器制动能力稳定性有着重要影响，因为在制动过程中会产生大量的热，导致制动器工作表面的温度急剧上升，摩擦系数急剧下降，从而最终导致制动能力下降。同时，高温会使得制动器摩擦片的磨损加剧

。所以热稳定性对于制动器亦相当重要。盘式制动器的摩擦系统主要是由制动盘和摩擦片组成，两者的粗糙表面在制动过程中相对滑动，使得两者表面的粗糙颗粒之间相互挤压和粘附，最终制动盘和摩擦片的表面磨损并伴随着大量的摩擦热。

制动盘各个点上的温度集合和应力集合称之为制动盘的温度场和应力场。制动盘的温度场会通过温度应力影响制动盘的应力场分布，而制动盘的应力场通过应变影响了摩擦过程中的温度场分布。一般认为，制动盘的温度场和应力场在制动过程中是一个热-结构耦合的过程。在早期的制动过程分析中，是将制动盘的温度场和应力场分开来研究的，后来通过与实际的实验相比较，发现通过热-结构耦合理论可以更加准确地描述制动过程中制动盘温度场和应力场的变化情况

。

本文借助有限元方法研究了多工况下某不锈钢制动系统制动过程中温度场和应力场的分布情况，并以热-结构耦合分析结果为基础，对制动盘结构进行基于响应面法的结构优化设计。

本试验采用柱端加载装置进行加载，试验加载装置如图2所示。在柱下端设置固定铰约束，左右梁端设置链杆约束，水平荷载由MTS电液伺服作动器施加，竖向荷载由稳压千斤顶施加，在千斤顶底座与反力梁之间设置滚轮，以保证在水平加载过程中千斤顶能跟随柱顶实时水平移动。图3为试验加载装置现场。

1 制动系统有限元模型建立

1.1 制动系统模型构建

制动系统由一块刹车盘和两块对称的来令片组成。制动盘厚度为2.5mm，来令片厚度为3mm。目前，制动盘散热主要是通过在制动盘轴向上添加绕制动盘轴线均布的“圆柱形”或“长条状”散热孔来提高制动盘散热效果。故在制动盘表面构建两层直径为4mm，每层均布36个的散热孔。刹车系统的有限元模型直接在WORKBENCH DM模块中构建，制动系统基本尺寸及结构如图1所示。

在WORKBENCH处理结果中提取9种模型的温度场数据，绘制相同转速下，不同制动压力时制动盘的温度场曲线，如图3所示。

1.2 制动系统各部件材料定义

从图3可以看出：在开始制动的极短时间内，制动盘表面最高温度快速上升，经过一段时间后，制动盘表面温度逐渐趋于平稳；在制动盘温度稳定阶段，最高温度曲线出现一定起伏，说明散热孔对制动盘散热起到促进作用。在制动盘转速为90rpm，制动压力为3MPa的制动工况下，温度曲线起伏较为明显，说明在高转速高制动压力情况下，散热孔散热作用才可能有效发挥，为了验证该假设的合理性，在WORKBENCH中模拟“90rpm和1MPa”和“90rpm和3MPa”(模型7和模型9)连续“点刹”3次的工况。整个制动过程为4s，每次“点刹”间隔时间为0.5s，制动盘表面温度场云图如图4所示，制动盘表面温度曲线如图5所示。

由于WORKBENCH自动划分网格使用的单元类型不包含温度自由度，需要用APDL命令流更改单元自由度，使用solid226单元进行网格划分，并使用牛顿-拉菲迅完全积分法进行求解计算。

1.3 定义边界条件

本文以制动压力分别为1MPa、2MPa、3MPa，制动盘转速为30rpm、60rpm、90rpm，构建了9种制动模型，对制动系统的热-结构耦合分析，制动模型如表3所示。

实行最严格水资源管理制度作为一项战略决策，意义非凡。要切实为“三条红线”的划定和实施提供技术支撑，保障项目建设质量和运行安全是关键。

1.4 有限元分析假设

对表3中的制动盘转速为90rpm时的模型7、8、9进行有限元分析，得到制动盘表面温度场分布如图2所示。从图2可以看出：制动盘温度较高区域主要集中在接触位置，为了使模拟条件更接近真实的“点刹”制动情况，制动时间设置为1s，温度场分布云图大体上呈规则环形分布，热量来不及通过热传递或热对流这两种方式向制动盘内部传递，导致制动盘表面温升较大。

(1) 制动盘和来令片间的接触为面与面接触，忽略各自表面的粗糙度和摩擦表面的磨损情况；

(2) 由于制动时间较短，忽略制动系统工作过程中的热辐射现象；

(3) 制动压力均匀的分布在来令片上；

手术前两组神经功能缺损评分、格拉斯哥晕迷分值、血肿水平、FIM评分相近,P>0.05;手术后观察组神经功能缺损评分、格拉斯哥晕迷分值、血肿水平、FIM评分优于对照组,P<0.05。如表2.

(5) 各部件密度不随温度变化。

1.5 制动压力对制动系统温度场的影响

在摩擦制动过程中，由于产生的摩擦热与摩擦接触压力的大小存在着直接的关系，不同接触状态下温度分布的不均匀性导致物体的热变形差异，而这又会直接引起接触状态或接触压力改变，接触状态的改变反过来影响摩擦热流密度的大小分布。可知，摩擦制动器的摩擦热问题是温度场与应力场的耦合问题。由于存在诸多影响摩擦副相互作用的因素，为了提高计算效率，做出以下假设

：

SET k-cover问题中研究百分百覆盖,要将式(2)所对应的连通度条件作为一个约束条件在算法中实现,从而保证网络的连通度。

为了提高有限元分析精度，制动系统各部件使用材料本构模型。与制动盘和来令片热-结构耦合相关的物理量有：密度、热膨胀系数、导热系数、比热、杨氏模量和泊松比。两种材料本构模型参数分别如表1、表2所示。

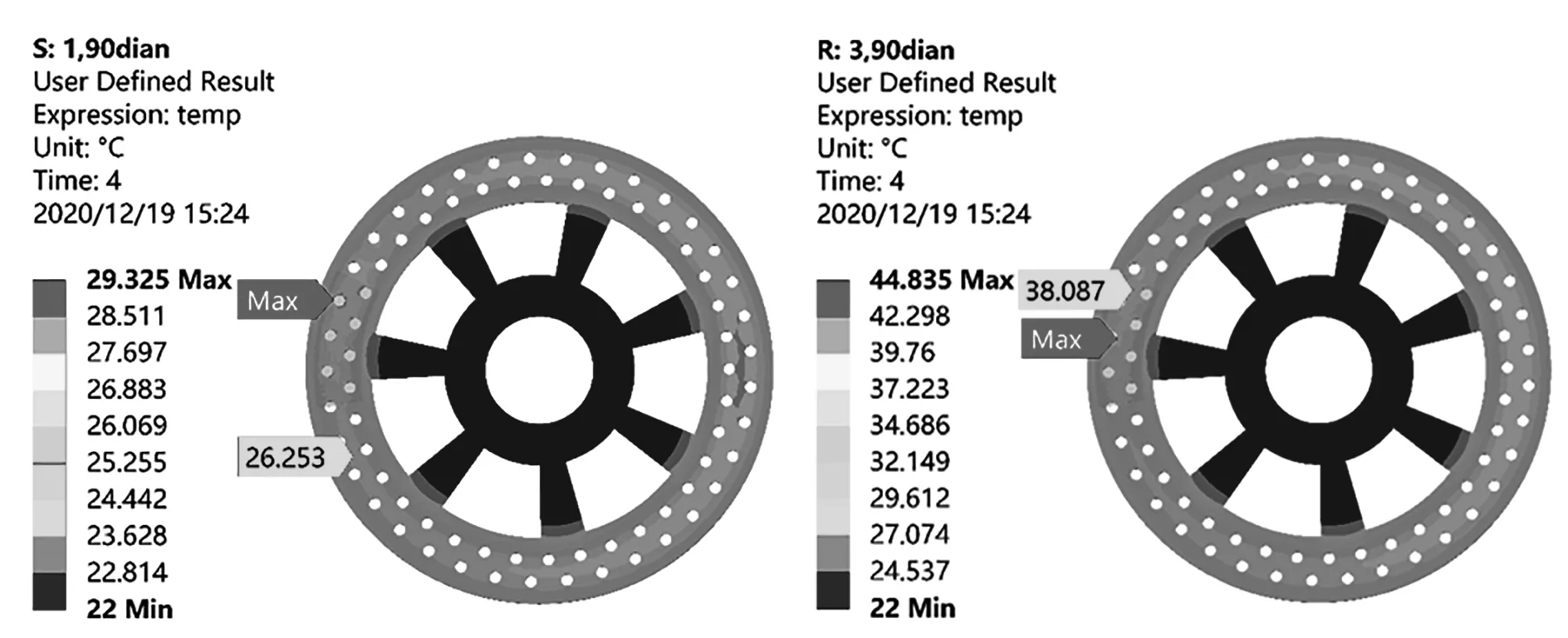
从图4和图5可以看出：制动时间为4s时，模型7和模型9中制动盘最高温度分别为29.3℃和44.8℃，且温度最高位置均在散热孔上；温度带分布情况与低载荷制动条件的并没有太大区别，温度带中间区域位置温度大致相同，温度分别为26.3℃和38.1℃；两种工况下，制动盘上最高温度曲线变化曲线具有相似的分布规律。随着制动盘转动，在1s时，制动压力开始减小，制动盘温度开始降低；在1.5s时，再次添加制动压力，制动盘温度开始上升。总体上制动盘温度呈上升趋势。但是，制动结束后，模型7温升约为7℃，而模型9温升约为23℃。

2 基于响应面法的制动盘结构优化

从WORKBENCH后处理结果中提取制动时间为4s时，模型9中制动盘的应力分布情况和最大应力变化曲线，如图6和图7所示。

从图6可以看出，制动盘在本文研究的最大载荷情况下，最大冯-米塞斯应力约为117.33MPa，远小于制动盘许用应力260MPa，所以该制动盘具有较大的优化设计潜力。

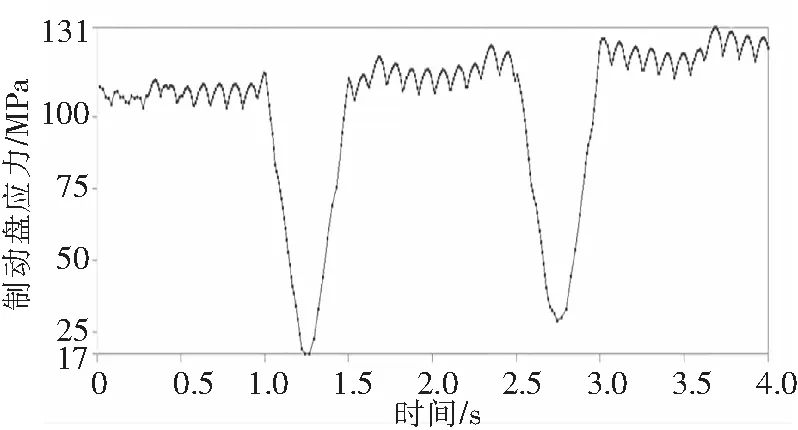
图7为直接从WORKBENCH后处理结果中截取的制动盘应力变化趋势图，从图中可以看出，在1s和2.5s时，制动盘应力开始急剧下降；从1.25s和2.75s开始，应力快速变大，与模拟的工况条件符合。同时，制动盘最大应力呈“波浪”形变化。为了节约计算成本，对模型3在1s制动时间的工况下，对制动盘结构进行优化。

(4) 摩擦制动过程为库仑摩擦，摩擦系数为定值；

种子发芽适宜温为25～30℃，低于15℃不易发芽，低于10℃或超过35℃发芽停止，辣椒播种后，床内温度白天要保持25～30℃，夜间保持在 15～20℃，经 5～7天苗可出齐，

湿法回收技术是通过使用适当的酸碱溶剂将电极片或电极粉料溶解到液体里，再进行分离萃取、沉淀分离，获取相应的金属化合物。湿法回收工艺的重要部分是浸取过程，即用无机酸或有机酸作为浸取剂，双氧水等作为还原剂将电极固体金属以离子的形式转移到酸溶液中。

2.1 响应面法简介

响应面法是指通过一系列确定性实验，用多项式函数来近似隐式极限状态函数，然后通过合理地选取试验点和迭代策略，来保证多项式函数能够在失效概率上收敛于真实的隐式极限状态函数的失效概率

。其基本思想是：通过一系列确定性实验，用多项式函数来近似隐式极限状态函数。通过合理地选取试验点和迭代策略，来保证多项式函数能够在失效概率上收敛于真实的隐式极限状态函数的失效概率。WORKBENCH中，基于响应面法的优化设计流程如图8所示。

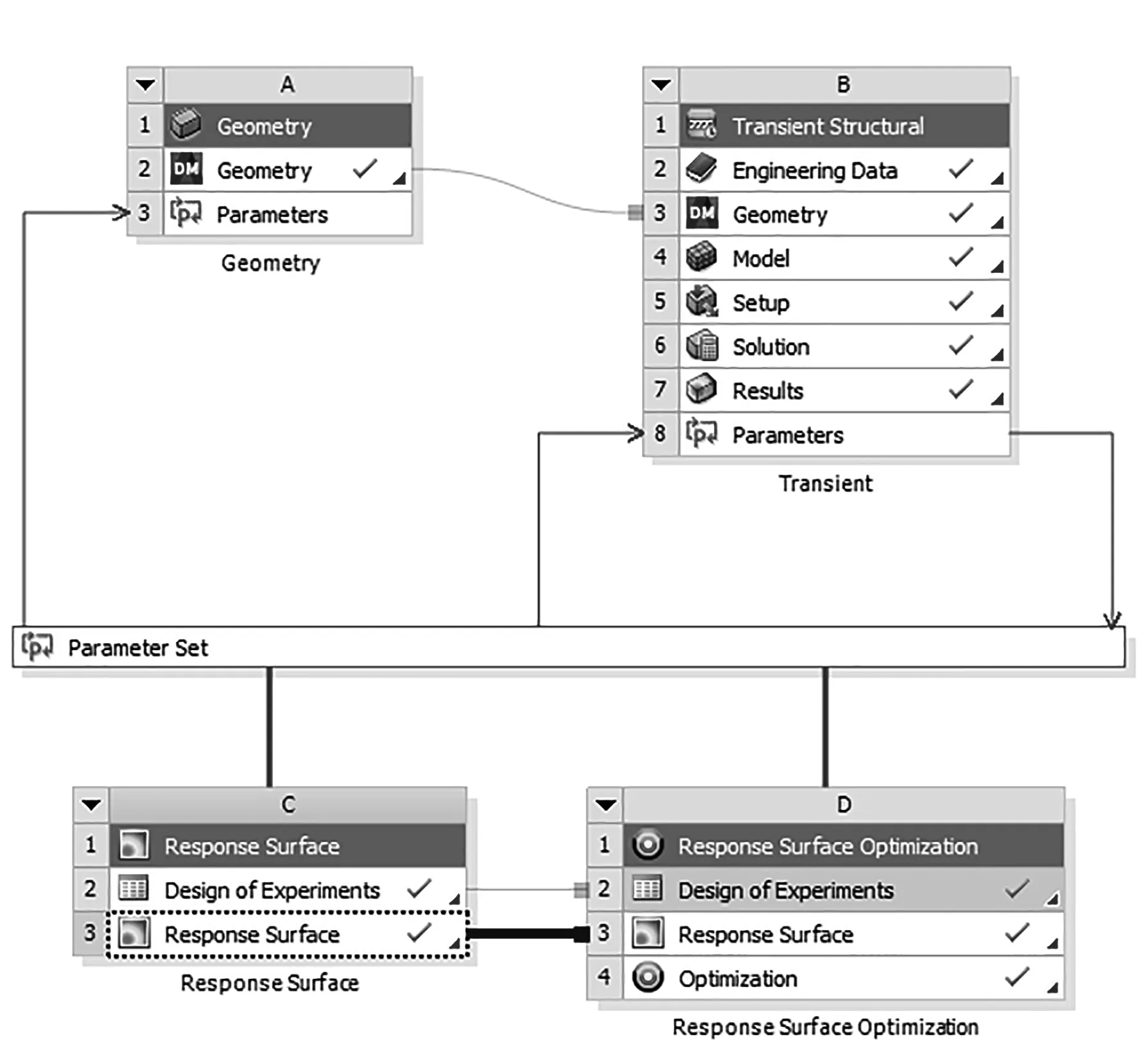
2.2 基于响应面法的制动盘结构优化设计

在WORKBENCH DM模块中，分别定义参数化设计变量，分别是散热孔直径和散热孔圆周阵列数量。在热-结构耦合分析结果中，以制动盘最高温度和最大应力作为设计目标。

实验设计时，将内、外两排散热孔设定为直径相等，直径变化范围为3.6mm至4.4mm(定义为P4)，将内外两派散热孔阵列数量设定为12到40个(内外分别定义为P2和P1)。此外，将制动盘最高温度定义为P3，最大应力定义为P6。计算后的得到的实验设计点如图9所示。

从图9可以看出，在设计的15个设计点中，当P1、P2、P4分别为24、24、36时，制动盘温度较低，为32.2℃，降低了12%；当P1、P2、P4分别为36、16、3.7时，制动盘最大应力最低，为112MPa，降低了4%。可以发现，散热孔直径和数量对最高温度影响较大，而对最大应力的影响较小。

在WORKBENCH中构建的散热孔数量与制动盘温度的响应面模型如图10所示。从结果的变化趋势看，随着散热孔数量的减少，制动盘温度逐渐降低，约在P1、P2为20时，制动盘温度最低。图11为散热孔直径对制动盘温度的影响趋势图。从图中可以看出，随着散热孔直径增大，温度逐渐降低。

3 结论

基于有限元仿真技术，使用材料本构模型，分析了制动压力与制动盘转速对制动系统温度场的影响机理，发现在高转速高制动压力情况下，散热孔散热作用才可能有效发挥。

1.3.2 移栽密度筛选试验 试验设4个处理：2万株 /hm2、4 万株 /hm2、6 万株 /hm2、8 万株 /hm2。每个处理重复3次，小区面积为30 m2。

利用响应面法对“制动载荷为3MPa，转速为90rpm”工况下，对制动盘结构进行了优化设计。观察在响应面法设计的15个样本点及其分析结果发现：散热孔直径及阵列数量对重载工况下制动盘的应力场分布影响较小，但对温度场分布影响较大。适量的散热孔结构可以有效降低制动盘温度，但是过多或过少都不利于降低制动盘温度，最优的散热孔排布为每层均布20个。在散热孔直径为3.6mm至4.4mm之间，随着散热孔直径增大，制动盘温度逐渐降低。

[1]左建勇,刘家良,胡果,顾亦豪.基于瞬态温升仿真的列车制动盘结构研究[J].机械设计与制造工程,2018,47(09):13-18.

[2]陈昶,张建军,陈睿.制动盘结构参数对温度场和应力场的影响研究[J].西南师范大学学报(自然科学版),2018,43(04):109-115.

[3]杨玥. 基于神经网络的盘式制动器热—结构有限元分析结果预测模型研究[D].吉林大学,2013.

[4]黄风山,高雅妍,王立新,翟利刚.仿生制动盘热-结构耦合场的ANSYS仿真分析[J].江苏大学学报(自然科学版),2015,36(04):392-397.

[5]何剑敏,叶燕飞,杨建,盛枫.汽车钢制车轮的响应面法优化设计[J].机械设计与制造,2022(01):172-176.

[6]王登峰,张帅,陈辉,汪勇.基于疲劳试验的车轮拓扑优化和多目标优化[J].汽车工程,2017,39(12):1351-1361+1374.