基于查询代价的两级轨迹数据划分算法

刘梦男,许建秋

（南京航空航天大学 计算机科学与技术学院,南京 211106）

0 引 言

近年来,随着物联网和移动互联网的不断发展,产生和收集大量轨迹数据变得可行.轨迹数据在路径推荐、路况预测和城市规划智能决策等领域有着重要的应用.轨迹数据具有重要的社会和应用价值.因此,对轨迹数据的存储、查询、处理和分析变得越发重要.

轨迹数据从采集到应用的过程中,存在很多问题亟待解决,由此出现了很多处理轨迹数据的技术.原始轨迹数据存在很多噪声和冗余,需要使用数据清洗、轨迹压缩等技术进行预处理再转化为校准轨迹.校准轨迹需要通过移动对象数据库管理系统进行存储、索引和查询等处理.对处理后的数据进行数据挖掘、隐私保护等操作后获得有价值的信息.轨迹数据划分是一种轨迹数据处理的方法,应用十分广泛.轨迹数据划分不仅可以通过划分原始轨迹数据来提高数据的索引和查询效率,还可以用于轨迹数据信息的提取和挖掘.本文的研究重点: 通过对轨迹数据进行划分使索引结构高效地支持查询.

在移动对象数据库中,轨迹数据通过单个三维最小边界矩形(Minimum Bounding Rectangle,MBR)来近似表示.这种近似方法会导致大量空白,造成查询效率的低下.在查询过程中,过多的空白会使查询窗口与MBR 相交,但并不与轨迹数据相交.图1 所示为轨迹数据划分对查询的影响,其中黑色圆点连线为轨迹.如图1(a)所示,查询窗口q1和查询窗口q2与轨迹数据的MBR 相交但并不与轨迹相交,这样会造成多余的I/O (Input/Output)操作,降低查询效率.轨迹数据划分可以将轨迹数据分割为独立的子轨迹,再通过MBR 近似划分后的子轨迹.可以很直观地看出,轨迹数据划分后的MBR要小于轨迹未划分的MBR.这样就可减少通过MBR 近似轨迹数据带来的空白体积,减少不必要的相交来提高查询的效率.如图1(b)所示,轨迹数据划分为子轨迹后,q1和q2不与轨迹的MBR 相交.

图1 轨迹数据划分对查询的影响Fig.1 Impact of trajectory partitioning on queries

为了能有效地处理基于轨迹的查询,需要支持轨迹数据查询的索引结构[1-3].R-tree[4]作为1 种常见的时空索引结构,可通过比较查询窗口与结点的MBR,逐步找到与查询窗口相交的数据.通过轨迹数据划分将轨迹数据划分为子轨迹可以减少数据层面的磁盘I/O,提高查询的效率.但引入划分会使Rtree 索引存储的MBR 增多,索引的规模变大,在查询过程中,会增大索引目录层面的磁盘I/O.因此,需要使用合适的R-tree 构建方法,将时空范围接近的子轨迹组织到同一结点中,减少索引目录级别的磁盘I/O.

基于此,本文提出了两级轨迹数据划分算法(Two-Level Trajectory Data Partition Algorithm,TLPA): 在第一级划分算法中,使用基于优化MBR 的轨迹数据划分算法将轨迹数据划分为子轨迹,使用子轨迹的MBR 来近似轨迹数据,进而减少MBR 的空白体积,提高近似效果,减少数据层面的磁盘I/O 来提高查询效率;在第二级划分算法中,使用基于网格的区域划分算法,将子轨迹按照时空范围划分到相应的网格中,并在此基础上提出R-tree 构建方法,将时空范围接近的子轨迹组织到同一结点中,减少索引目录层面的磁盘I/O.通过两级划分算法,减少了数据层面和索引目录层面的磁盘I/O 数量,提高了查询效率.本文使用真实出租车GPS 数据集进行实验,与基于轨迹段平均个数的轨迹数据划分算法(Based on Average Number of Partition Algorithm,BNPA)和基于组合运动特征的轨迹数据划分算法(Based on Combined Movement Features,BCMF)进行了比较.结果显示,本文的两级轨迹数据划分算法具有更好的查询性能,查询效率较BNPA 平均提升了43.0%,较BCMF 平均提升了30.5%.

本文后续结构: 第1 章简要介绍轨迹数据划分的相关工作;第2 章定义轨迹数据划分和查询的相关问题;第3 章介绍两级轨迹数据划分算法;第4 章介绍基于划分算法的R-tree 构建方法和查询处理;第5 章将本文提出的算法与现有的轨迹数据划分方法进行分析和比较;第6 章是总结和展望.

1 相关工作

轨迹数据划分算法主要分为3 种: 基于时间的轨迹数据划分算法、基于特征点的轨迹数据划分算法和基于区域的轨迹数据划分算法.Yue 等[5]采用基于时间的哈希策略来保证分区平衡和更少的分区时间,从而提高海量轨迹数据集的范围查询效率.Tang 等[6]根据速度变化提取变化点,根据停留时间提取停留点,将欧几里得垂直距离指标与运动方向相结合,将变化点和停留点、识别方向突变的点作为特征点,并使用这些特征点进行轨迹数据划分.Morteza 等[7]提出了将由轨迹的最小边界矩形(MBR) 定义的轨迹区域划分为包含运动对象 GOI (Geometry of Interest) 的网格的方法,该方法基于提取的 GOI 和划分的轨迹区域,可以仅使用相交几何算子提取轨迹的访问地点的顺序(Sequence of Visited Locations,SVL).

按照应用场景分类,轨迹数据划分算法主要分为3 种: 通过轨迹数据划分来进行数据分析,提取出轨迹数据中的离群点;通过区域划分策略来解决空间轨迹的聚类问题;通过对移动对象轨迹进行划分使索引结构高效地支持时空范围查询.Lee 等[8]提出了轨迹离群点的划分和检测框架,该框架将1 条轨迹数据划分为1 组线段,然后针对轨迹离群点检测外围线段,并基于这种划分检测框架,开发了轨迹异常值检测算法(TRAjectory Outlier Detection,TRAOD).Masciari[9]提出了基于合适的区域划分策略和合适度量的高效聚类技术用于解决空间轨迹的聚类问题.Hadjieleftheriou 等[10]首先提出通过引入人工分割来划分轨迹数据;由于使用MBR 近似时空对象时会产生大量空白体积,这将导致传统的多维索引效率降低,然后提出了可以将时空对象分割成预定数量的轨迹段的轨迹数据划分算法,使划分后的轨迹的MBR 体积最小,从而提高索引的查询效率.Rasetic 等[11]提出的正式的代价模型,用于估计给定的查询大小和轨迹的任意分割来评估时空范围查询所需的I/O 数量;此模型引入了动态规划算法来分割1 组轨迹,这样使相对于平均查询大小的预期磁盘I/O 数量达到了最小化.

2 问题描述

本章对本文所使用的术语进行了定义和解释,并给出了文中使用的符号及其释义.符号和释义详见表1.

表1 符号表Tab.1 Symbol table

定义 1轨迹: 轨迹通常是由时间和二维空间的函数进行建模.在数据库系统中,用时间单元序列来表示轨迹.假设轨迹由T=〈u1,u2,···,ut〉来表示,其中ui是1 个轨迹段,由〈ti,ti+1,xi,yi,xi+1,yi+1〉表示,ti和ti+1分别为1个时间间隔的开始时间和结束时间,(xi,yi) 和 (xi+1,yi+1) 分别为开始时间的空间位置和结束时间的空间位置.

定义 2轨迹MBR: 轨迹MBR 是指以三维坐标表示的轨迹数据的最大范围.

定义 3轨迹数据划分: 轨迹T=〈u1,u2,···,ut〉可以通过多种可能的方式(从T中选择m个分割点),沿其离散时间维度分割成m+1段,其中 0＜m ＜t.用T[b,d]表示1 条以ub开头、ud结尾的子轨迹.这样划分后的轨迹可以表示为T(m)={T[1,i1],T[i1,i2],···,T[im,t]},划分后的m个子轨迹取并集仍能组合生成原始轨迹.

定义4时空范围查询: 给定轨迹数据集S,时间范围 (ts,te) (ts为开始时间,te为结束时间),空间范围(xl,yl,xu,yu) ((xl,yl)表示空间范围的左下坐标,(xu,yu) 表示空间范围的右上坐标),查询所有满足t在区间[ts,te]、位置 (x,y) 在空间范围(xl,yl,xu,yu)中的时空对象.

3 算法描述

3.1 查询代价分析

给定1 条划分后的轨迹T(m),假设轨迹段的MBR 是独立存储的,查询窗口和每个轨迹段的MBR相交都要耗费1 个独立的磁盘I/O.则轨迹与查询窗口 (q)相交的磁盘I/O 次数 (D) 的计算公式[12]为

为求解 Intersect(T(m),q),下面以二维情况为例,给出推导过程.由于查询窗口的大小和位置是未知的,故不能准确求出空间对象MBR 与查询窗口的相交次数,需要用相交的概率来估计相交次数.在二维空间中,假设查询窗口q=(Δx,Δy) 等可能地出现在整个数据空间的各个位置,如图2 所示,其中,q.Δx和q.Δy分别表示查询窗口x维度的长度和查询窗口y维度的长度.图2 中,查询窗口 (q) 与MBR 相交当且仅当查询窗口的中心落入区域α.由于查询窗口是等可能地出现在数据空间的各个位置,因此,相交的概率为区域α的面积与总数据空间面积的比值,其中区域α为MBR 沿x,y维度拓展查询窗口大小的一半得到的区域.把这个区域命名为拓展MBR.空间对象的拓展MBR 越大,说明MBR 的近似效果越差,导致空间对象与查询窗口相交概率增大,相交次数也相应增大.这样会造成更多的不必要的相交,降低查询效率.因此,轨迹数据的最优划分要保证划分后的轨迹数据的拓展MBR 最小.

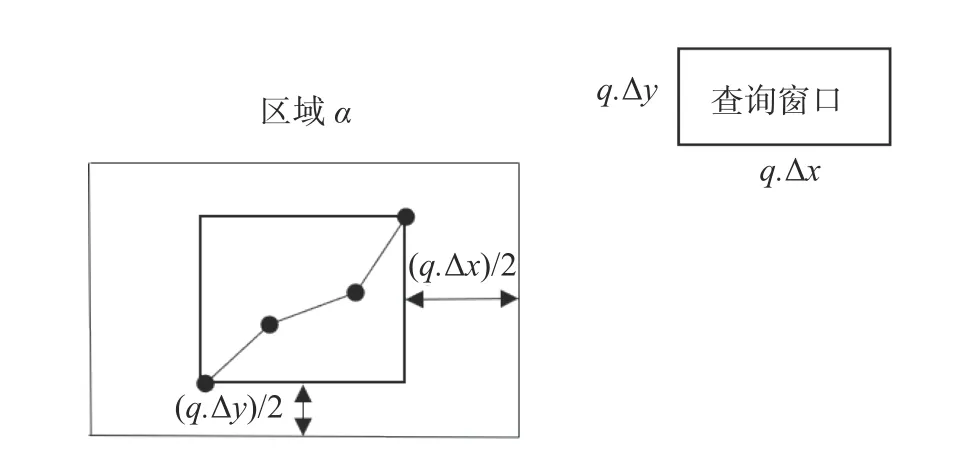
图2 轨迹数据的拓展MBRFig.2 Expansion MBR of trajectory data

显然,对于轨迹数据来说,增加划分段数会减少划分后子轨迹的MBR 总体积,但对于拓展MBR 来说,情况并非如此.拓展MBR 是将轨迹数据的MBR 沿x方向左右、y方向上下分别延伸X/2、Y/2 长度.当查询窗口较大时,增加划分段数会使轨迹数据通过拓展增大的体积大于划分导致的MBR 减少的体积.因此,在划分前需要通过查询窗口和轨迹数据来定量分析得到最优的划分段数.

基于上述分析,给出下列引理及证明.

引理 1给定二维空间对象O={o1,o2,···,om},oi为 (xi,yi,xi+1,yi+1) ,其中,xi+1＞xi,yi+1＞yi,当划分段数确定时,划分后的空间对象O的拓展MBR 面积(用Sn表示)与其MBR 面积(用SBO,n表示)满足

证 明设查询窗口在x,y维度上的大小分别为X,Y.假定划分段数为n(n＜m-1),则有多种可能的方式将O划分为n个子空间对象,表示为O=(O[1,k1],O[k1,k2],···,O[kn-1,m]) ,其中O[1,k1] 表示包含o1,o2,···,ok1的空间对象.将这些子空间对象近似为1 组MBR,表示为BO=(MBR(O[1,k1]),MBR(O[k1,k2]),···,MBR(O[kn-1,m]),O的所有可能划分情况表示为Gather(O,n)={(B1,B2,···,Bn)|∃k1,···,kn-1:B1=MBR(O[1,k1]),B2=MBR(O[k1,k2]),···,Bn=MBR(O[kn-1,m])}.O[1,k1] 的拓展MBR 大小S(O[1,k1]) 为

将所有子空间对象的拓展MBR 相加可以得到

其中,nXY+(ym+1-y1)X+(xm+1-x1)Y为定值,SBO,n为划分后的空间对象O的MBR 面积,BO ∈Gather(O,n).因此,当划分段数和查询窗口大小确定时,划分后的空间对象O的拓展MBR 面积(Sn)仅由其MBR 面积(SBO,n)决定.

引理 2给定二维空间对象O={o1,o2,···,om},oi为 (xi,yi,xi+1,yi+1) ,其中,xi+1＞xi,yi+1＞yi,O的最优划分段数 (使拓展MBR 面积最小的划分段数) 仅与查询窗口大小有关,且随着查询窗口的增大,最优划分段数从m逐渐减少到0.

证 明根据引理1 可知,当划分段数为n时,设O的最小拓展MBR 面积为

其中 Gather(O,n)为划分段数为n时,O的所有划分的集合.

当划分段数为n+1 时,

基于引理2 可以发现,仅通过oi的值就可以求出的值.因此,可以通过XY与的值获取m-1个分界点,将整个数据空间范围划分为连续的m个区间,其中每个区间对应查询窗口大小XY的具体范围和该范围下的最优划分段数;再通过引理1 就可以得出对应的划分方式,即为最优划分方式.

3.2 基于优化MBR 的轨迹数据划分算法

在数据库中,时间维度和空间维度被同等对待.因此,上述分析对于作为三维时空对象的轨迹数据同样适用.给定1 条轨迹T,查询窗口q=(X,Y,Z),其中X,Y,Z分别为q在x,y,t维度上的大小.使用ui的值则可求出最优划分段数对应的查询窗口大小区间和在该划分段数下的最优划分方式.

基于以上讨论,给出基于优化MBR 的轨迹数据划分算法.具体见算法1.

算法1 中: track 数组用于保存轨迹数据划分状态,初始化时插入0 和T.size,表示当前子轨迹只有1 条,为原始轨迹,当经过1 次循环找到1 个划分点后,插入track,记录当前划分状态;result 数组用于保存划分方式及对应的查询窗口区间,在循环结束后,作为partition()函数的参数用于划分;partition()函数通过使用给定的查询窗口大小和result 数组得到最优划分方式.

通过算法1,可以得出每条轨迹数据针对不同查询窗口大小的最优划分方式.对于整个轨迹数据集中的每个轨迹数据均采用算法1,最后可以得到整个数据集上的最优划分.在实际应用中,查询窗口的大小不能预先确定,需要通过数学统计及分析预先得出查询窗口的平均大小.在平均大小不能很好地代表查询窗口的大小时,可以将查询窗口大小的范围与求出的区间进行比较,选出相交区域最多的区间进行划分.这样可以保证划分后的轨迹数据在尽可能大的查询窗口范围内其查询效率最优.在不能预先获取查询窗口大小的情况下,可以将整个查询窗口大小范围划分为多段,作为基准分别建立Rtree;在查询过程中,通过具体查询的窗口大小选择对应的R-tree.对于基于优化MBR 的轨迹数据划分算法,可以得到每条轨迹数据的划分方式及对应的查询窗口区间.因此,建立不同查询窗口大小范围的多条R-tree 的时间代价会低很多.

3.3 基于网格的区域划分算法

基于优化MBR 的轨迹数据划分算法可以根据预期查询窗口大小将轨迹数据划分为多条子轨迹,并通过子轨迹的MBR 近似轨迹数据,减少数据层面的磁盘访问次数.但R-tree 索引是将多条轨迹组织到叶子结点中来回答查询,数据层面的优化不能保证构建索引后仍然是最优的.因此,本文提出了基于网格的区域划分算法: 将通过基于优化MBR 的轨迹数据划分算法划分后的子轨迹进行分组,把时空范围接近的子轨迹数据划分为1 组;针对分组后的子轨迹设计R-tree 构建算法,提高索引目录层面的查询效率.

基于网格的区域划分算法: 首先,将时空范围划分为多个大小相等的不重叠的网格单元,每个单元仅存放完全包含在单元内的轨迹数据,如果轨迹数据穿过时空分割边界,则轨迹数据在边界处进行划分,并插入2 个网格单元中 (图3);然后,将落入网格单元中的轨迹数据作为元组存储到数据文件中,每个数据页仅包含来自同一网格中的轨迹数据,网格单元存放这些数据页的信息以用于查找.

图3 轨迹数据划分示意图Fig.3 Schematic diagram of trajectory partition

网格划分粒度是1 个很重要的参数: 一方面,如果网格单元的范围过大,会导致不同网格间的时空区分度低,增加R-tree 构建的难度;另一方面,如果网格划分得非常精细,那么跨越网格边界的轨迹数就会增加,这反过来又会增加划分开销.选取原始轨迹数据的平均大小作为划分粒度既不会使网格空间范围过小,引入大量的划分,也不会使网格空间过大,降低时空区分度.

基于网格的区域划分算法使每个网格单元中的轨迹数据的时空范围相近,且每个网格单元数据量较少,便于R-tree 结点的组织与构建.

4 R-tree 构建和查询处理

4.1 R-tree 构建

常规的R-tree 的构建方法有2 种,分别为自底向上[13-14]和自顶向下[15]的构建方法.自顶向下的构建方法采用插入的方式逐个将对象插入R-tree 结点,这种构建方式存在一些缺点,如较高的构建时间、较低的结点利用率等.因此,本文的R-tree 构建方法采用自底向上的R-tree 构建方法,将划分后的子轨迹按照一定的规则构建R-tree.

在使用基于网格的划分算法将子轨迹分组后,每个网格中的子轨迹时空范围相近.因此,Rtree 的每个叶子结点仅存储来自同一网格中的子轨迹,不仅提高了构建效率,而且使时空范围相近的子轨迹存放到同一叶子结点中,还提高了索引的查询性能.

基于网格划分的构建方法的示意图如图4 所示.

图4 基于网格划分的构建方法示意图Fig.4 Schematic diagram of the construction method based on a mesh partition

R-tree 结点组织方法的基本思想: 首先,选取网格中时间维度最小的子轨迹,将其作为只有1 个条目的叶子结点,通过计算,将网格中其余子轨迹插入叶子结点后叶子结点MBR 增量,选取f-1 个增量最小的子轨迹构建叶子结点;然后,从剩余子轨迹中继续选取时间维度最小的子轨迹,重复上述过程,直到网格中所有子轨迹均插入叶子结点,再进入下个网格,生成所有叶子结点;最后,将叶子结点看作新的条目,按照上述过程递归生成中间结点,直到生成根结点.

4.2 查询处理

R-tree 的叶子结点存储的条目为是轨迹的唯一标识符TupleID 和MBR.在查询过程中,通过比较结点MBR 与查询窗口是否相交来逐步获取轨迹MBR 与查询窗口相交的条目,生成候选轨迹列表.由于R-tree 存储的是划分后的子轨迹,因此,候选轨迹列表中可能会出现属于同一轨迹的多条子轨迹.所以在生成候选轨迹列表后,要对列表进行去重操作;去重后,使用TupleID 获取具体的轨迹信息,然后再进行相交判断,获取与查询窗口相交的轨迹.

基于优化MBR 的轨迹数据划分方法是通过与查询窗口相交的次数的分析得到的,它适用于时空范围查询.对于轨迹k-近邻查询、轨迹相似性查询等查询方式,同样可以使用合适的查询窗口得到结果.出于篇幅考虑,本文不做进一步的讨论.

5 实验评估

5.1 前期准备

实验数据集使用北京市2008 年3 月2 日至3 月8 日的10 357 条出租车GPS 轨迹数据.轨迹数据的采样点为1 083 560 个.实验在Ubuntu14.04 环境下进行,采用C++语言编写,利用可拓展的移动对象数据库系统Secondo[16]框架进行实验评估.CPU 为Intel Xeon(R) 1.90 GHz × 6,GPU 为NVIDA Corporation GM107GL [Quadro K2200],32 GB 内存.

5.2 实验及结果

实验首先采用第3 章提出的轨迹数据划分算法分别对数据集中的轨迹数据进行逐条划分,查询窗口大小分别设置为1%、5%、10%数据空间大小;然后将划分后的轨迹数据用第4 章提出的R-tree 构建算法构建R-tree;最后用中央处理器运行时间(CPUtime)来衡量查询效率.本文将使用基于组合运动特征的轨迹数据划分算法(BCMF)和基于轨迹段平均个数的轨迹数据划分算法 (BNPA)与本文提出的两级轨迹数据划分算法(TLPA) 进行了对比实验,并对使用Secondo 中的Bulkload 构建方法和基于网格划分的构建方法进行了对比实验.BNPA 是基于平均度量的轨迹数据划分算法,它分别使用轨迹数据的平均轨迹段个数进行划分,划分后的子轨迹的轨迹段个数不超过平均轨迹段个数.

图5、图6、图7 分别给出了本文的轨迹数据划分算法(TLPA)与基于轨迹段平均个数的轨迹数据划分算法(BNPA)和基于组合运动特征的轨迹数据划分算法(BCMF),在不同查询窗口大小下的轨迹范围查询效率的结果.图5、图6、图7 中,横轴为查询窗口大小,纵轴为查询所需的CPUtime,TLPA1%、TLPA5%、TLPA10%分别表示TLPA 的查询窗口大小设置为1%、5%、10%数据空间大小.从图5、图6、图7 中可以看到,TLPA在查询窗口大小为整个数据空间的1%、5%、10%时查询效率都优于BCMF 和BNPA 这2 种算法.其中,TLPA 在查询窗口大小为整个数据空间的1%时(图5),相比BCMF 查询所需的CPUtime 减少了11.7%,相比BNPA 减少了55%;TLPA 在查询窗口大小为整个数据空间的5%时(图6),相比BCMF 查询所需的CPUtime 减少了30%,相比BNPA 减少了62%;TLPA 在查询窗口大小为整个数据空间的10%时(图7),相比BCMF 查询所需的CPUtime 减少了50%,相比BNPA 减少了12%.在给定查询窗口大小的情况下,与BCMF 和BNPA 相比,TLPA 具有更好的查询性能,查询效率较BCMF 平均提升了30.5%,较BNPA 平均提升了43%.BCMF 在查询窗口较小时查询性能较好,原因是BCMF 的划分粒度很细,会将轨迹数据划分为较多的子轨迹,相当于针对较小查询窗口的最优划分.BNPA 的划分粒度较粗,会将轨迹数据划分为较少的子轨迹,相当于针对较大查询窗口的最优划分,在较大查询窗口时的查询效果更好.

图5 BCMF、BNPA 和TLPA1%在不同查询窗口大小下的查询效率Fig.5 BCMF,BNPA,and TLPA1% query efficiency under different query window sizes

图6 BCMF、BNPA 和TLPA5%在不同查询窗口大小下的查询效率Fig.6 BCMF,BNPA,and TLPA5% query efficiency under different query window sizes

图7 BCMF、BNPA 和TLPA10%在不同查询窗口大小下的查询效率Fig.7 BCMF,BNPA,and TLPA10% query efficiency under different query window sizes

图8 给出了Bulkload 和基于网格划分的构建方法在构建R-tree 时的效果对比.TLPA5%算法划分后的轨迹数据分别使用了Bulkload 和基于网格划分的构建方法构建R-tree,并比较了在各个查询窗口大小下的磁盘访问(I/O)次数.从图8 中可以看到,使用基于网格划分的构建方法磁盘访问次数相比Bulkload 少了约20%,构建R-tree 效果更好.

图8 TLPA5% 分别使用Bulkload 和基于网格划分构建方法的I/OFig.8 I/Os of TLPA5% using bulkload and packing method based on cell partition

6 总结与展望

本文提出的两级轨迹数据划分算法,对轨迹数据进行划分使之可以高效地支持时空范围查询.基于两级轨迹数据划分算法,本文提出了R-tree 构建方法,对划分后的轨迹数据进行组织构建.使用此方法构建的R-tree 比使用Secondo 中Bulkload 构建得到的R-tree 回答范围查询的查询效率更高.本文主要介绍的是轨迹数据划分算法对范围查询的优化,但对于k-近邻查询和轨迹相似性查询等查询方式同样可以使用查询框来近似得到查询结果,未来可以对此做进一步的研究.