三参数异形椭球面方程、几何特征及应用前景
武周虎
(青岛理工大学 环境与市政工程学院, 山东 青岛 266033)
椭球面是一种二次曲面,它是椭圆在三维空间的推广[1],蛋形曲线[2-3]绕对称轴旋转180度形成蛋形曲面,常见的闭曲面类型有球面、椭球面、环形面和蛋形曲面等。世界各国具有代表性的蛋形仿生建筑有中国国家大剧院、日本东京巨蛋(Tokyo Dome)、英国埃克斯伯里蛋形(Exbury Egg)和印度孟买赛博蛋形(the Cybertecture Egg)等[4]。武周虎基于河流常系数对流扩散简化方程的解析解,推导出污染混合区等浓度线方程[5-6],据此定义了只有单对称轴的二参数平面闭曲线——异形椭圆(Wu’s 曲线)方程,讨论了异形椭圆的几何性质以及在交通隧道和水工隧洞设计中的应用[7-9]。异形椭圆作为重要的数学曲线,在日常生产生活中具有重要应用价值。
本文基于笔者创建的二维异形椭圆方程和三维对流扩散物质的等浓度面方程[10],定义纵向半长度、横向半宽度和垂向半高度3个独立参数,分别构建三维空间的Ⅰ型和Ⅱ型异形椭球面——2种三参数闭曲面方程,分析它们的几何特征,探讨它们的应用前景,为其推广应用提供理论支持。
1 异形椭圆
武周虎[7-9]创建的异形椭圆(见图1)方程为:
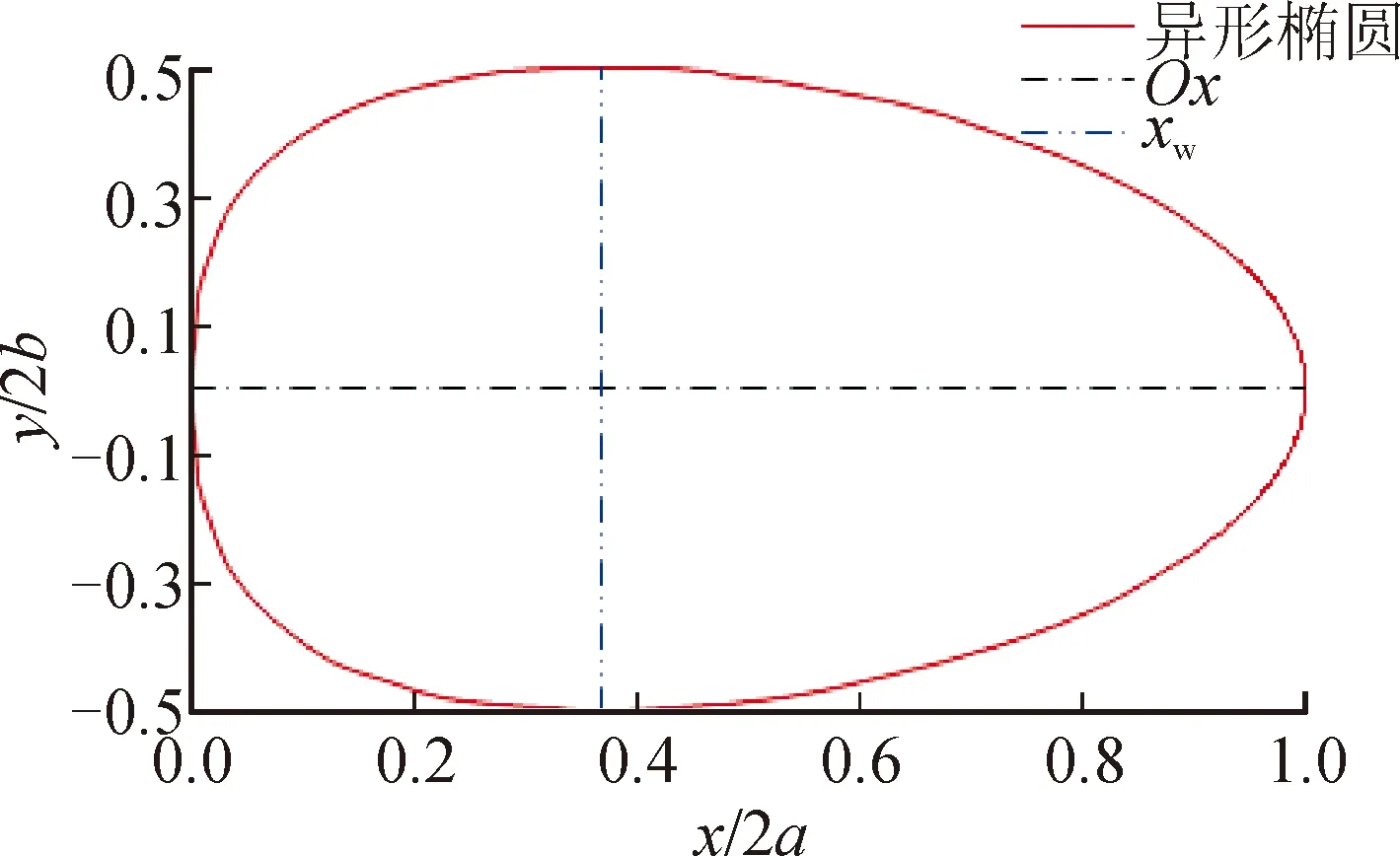
图1 归一化异形椭圆示意图Fig.1 Schematic diagram of a normalized heteromorphic ellipse
(1)
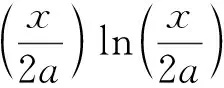
由图1可以看出,异形椭圆像一个变形的椭圆,在对称轴Ox的O端钝胖,远端锐瘦,它是只有单对称轴的二参数平面闭曲线。异形椭圆宽度(即最大宽度)相应的纵向坐标为xw=2a/e ≈0.368(2a),接近黄金分割比例,使图形产生美感。异形椭圆4个顶点坐标分别为(0,0)、(2a,0)、(2a/e,-b)和(2a/e,b)。
异形椭圆的面积等于其面积系数、长度和宽度的乘积[7-8],即有面积公式为:
S=μ(2a)(2b)
(2)
2 Ⅰ型异形椭球面
2.1 基本方程
基于武周虎[10]水库稳定点源简化三维对流扩散物质的等浓度面方程,定义三维空间的Ⅰ型异形椭球面方程为:
(3)
(0≤x≤2a,-b≤y≤b,-c≤z≤c)
式中:c为非对称轴(垂向坐标)z方向的半高度,其它符号同前。
当a=2.0、b=c=0.5时,由式(3)绘制Ⅰ型异形椭球体的三维建模横截面轮廓线,见图2(a);曲面体效果,见图2(b)。
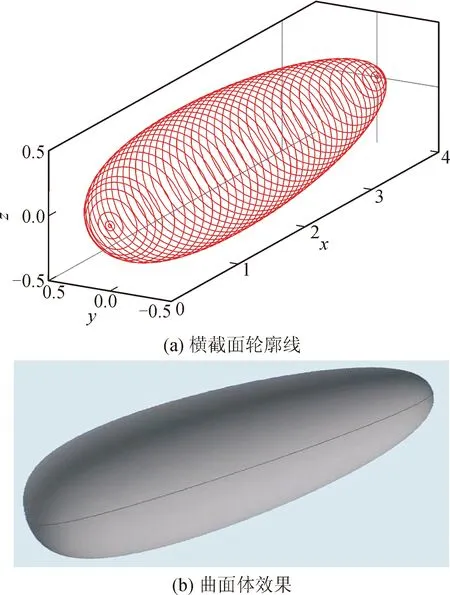
图2 Ⅰ型异形椭球体的三维建模Fig.2 3D modeling of a type I heteromorphic ellipsoid
2.2 几何特征分析
由式(3)和图2可以得到如下结果。
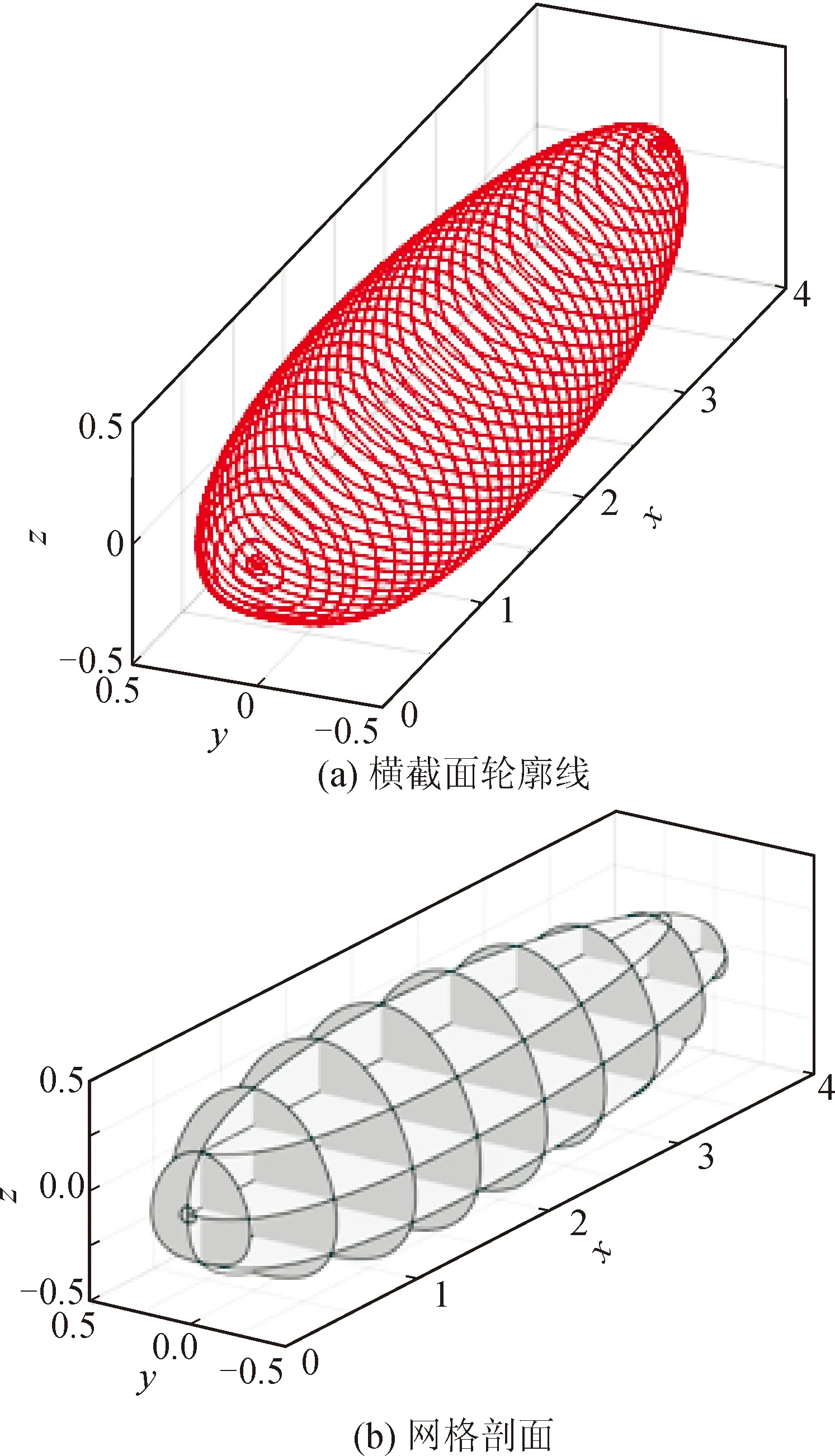
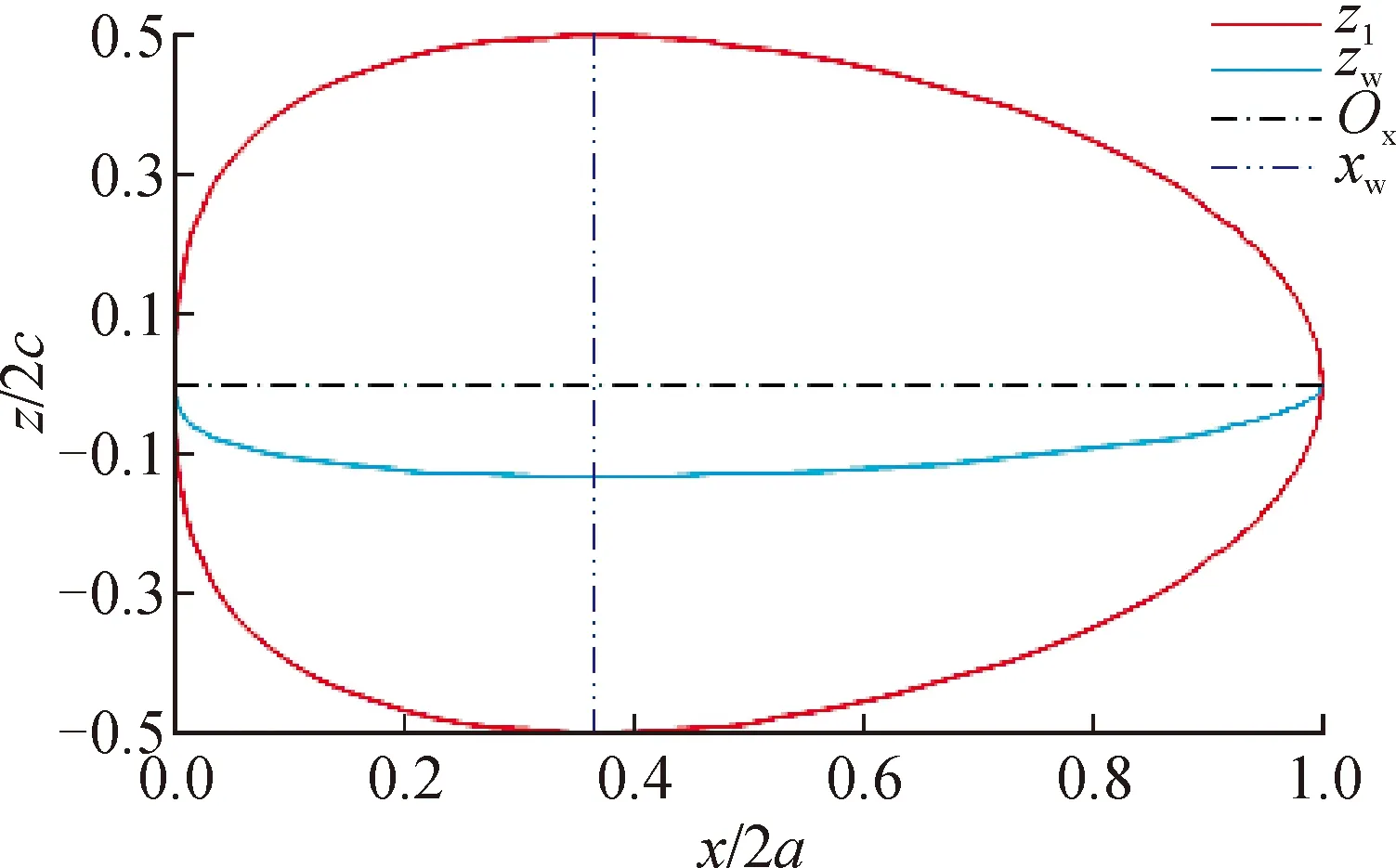
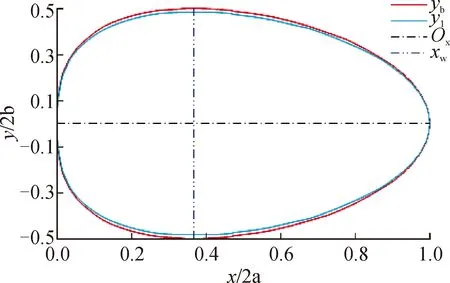
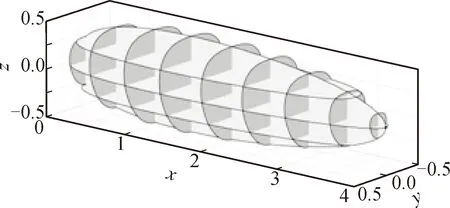
1) 当x=定值(0 (4) 该椭圆与Ⅰ型异形椭球面轮廓在yOz坐标面上的投影曲线重合。 2) 当y=0或z=0时,即在xOz或xOy坐标面上,Ⅰ 型异形椭球面的剖面曲线均为异形椭圆,该异形椭圆恰好是 Ⅰ 型异形椭球面轮廓在相应坐标面上的投影曲线。即在这两个坐标面上的剖面曲线为最大异形椭圆。 3) Ⅰ型异形椭球面左、右、前、后、下和上的6个顶点坐标分别为(0,0,0)、(2a,0,0)、(2a/e,-b,0)、(2a/e,b,0)、(2a/e,0,-c)和(2a/e,0,c)。 4) 当b=c时,Ⅰ型异形椭球面就是异形椭圆绕对称轴Ox的180度旋转曲面。 综上,在笛卡尔坐标系中,Ⅰ型异形椭球面的基本几何特征为:在yOz平行面上的横截面为椭圆,在xOy和xOz坐标面上的剖面曲线均为异形椭圆,在对称轴Ox的O端钝胖,远端锐瘦。 三维空间的Ⅰ型异形椭球体的体积等于其体积系数、半长度、半宽度和半高度的乘积[10],即有体积公式为: V=φabc (5) 将只有单对称轴的二参数平面闭曲线——异形椭圆在三维空间进行推广,定义纵向半长度(a)、横向半宽度(b)和垂向半高度(c)3个独立参数,构建Ⅱ型异形椭球面方程,使Ⅱ型异形椭球面在空间直角坐标面上的剖面曲线和俯视轮廓线均为异形椭圆。 在空间直角坐标系O-xyz中,过原点O三条坐标轴Ox、Oy、Oz的正方向符合右手规则,见图2。Ⅱ型异形椭球面方程构建的方法步骤如下。 1) 在y=0的坐标面xOz上,设定Ⅱ型异形椭球面的剖面曲线为关于Ox轴上下对称的异形椭圆,其方程为: (6) 或 (7) 式中:z1为Ⅱ型异形椭球面在xOz坐标面上剖面异形椭圆的垂向坐标,其它符合同前。 2) 当x=定值时,即在yOz的平行面上,设定 Ⅱ 型异形椭球面的横截面异形椭圆对称轴过Ox轴且平行于Oz轴。取横截面异形椭圆对称轴的下、上顶点坐标分别为(y=0,z=-|z1|)和(y=0,z=|z1|),即有横截面异形椭圆的对称轴垂向高度为2|z1|。设非对称轴横向半宽度为|yb|。 根据异形椭圆方程的基本形式,则有横截面异形椭圆方程为: (-|yb|≤y≤|yb|,-|z1|≤z≤|z1|) (8) 3) 在z=0的坐标面xOy上,设定Ⅱ型异形椭球面的俯视轮廓(横截面异形椭圆宽度)曲线为关于Ox轴前后对称的异形椭圆,其方程为: (9) 式中:yb为Ⅱ型异形椭球面在xOy坐标面上俯视轮廓异形椭圆的横向坐标。 4) 将式(7)和式(9)代入式(8)得到Ⅱ型异形椭球面方程为: (10) 定义域为:0≤x≤2a,-b≤y≤b,-c≤z≤c,其中a、b、c为任意正常数。 当a=2.0、b=c=0.5时,由式(10)绘制Ⅱ型异形椭球体的三维建模横截面轮廓线和网格剖面,见图3(a)~(b)。 图3 Ⅱ型异形椭球体的三维建模Fig.3 3D modeling of a type II heteromorphic ellipsoid 由式(6)~式(10)和图3可以得到如下结果。 1) Ⅱ型异形椭球面关于坐标面xOz对称,在xOz坐标面上的剖面曲线呈现为由式(6)或式(7)表示的异形椭圆。当xw=2a/e时,Ⅱ型异形椭球面的横截面对应的异形椭圆最大,由式(10)得到最大横截面异形椭圆方程为: (11) 该异形椭圆与Ⅱ型异形椭球面轮廓在yOz坐标面上的投影曲线重合。 2) 当x=定值时,Ⅱ型异形椭球面的俯视轮廓线宽度对应的垂向位置与对称轴下顶点之间的距离为2|z1|/e。则有,该垂向位置坐标为zw=(2/e-1)|z1|,将式(7)代入后整理得到zw的表达式为: (12) 图4给出由式(7)表示的Ⅱ型异形椭球面在xOz坐标面上的剖面异形椭圆(z1)和由式(12)表示的俯视轮廓线对应的垂向坐标(zw)曲线。 图4 xOz坐标面上的异形椭圆和俯视轮廓线对应的垂向坐标曲线Fig.4 A heteromorphic ellipse on the xOz coordinate plane, and the vertical coordinate curve corresponding to the top view contour 由图4和式(12)可知,Ⅱ型异形椭球面的俯视轮廓线对应的垂向坐标位于z<0的下部区域,其值随纵向坐标x的分布曲线为半高度(≈0.264c)的下半异形椭圆。据此得到,Ⅱ型异形椭球面的俯视轮廓线以下高度占同一横截面总高度的1/e≈0.368。 3) 当z=0时,由式(10)得到Ⅱ型异形椭球面的剖面曲线方程为: (13) 式中:y1为Ⅱ型异形椭球面在xOy坐标面上剖面异形椭圆的横向坐标。 图5给出由式(9)表示的Ⅱ型异形椭球面俯视轮廓异形椭圆(yb)和由式(13)表示的Ⅱ型异形椭球面在xOy坐标面上的剖面异形椭圆(y1)。 图5 xOy坐标面上的异形椭圆和俯视轮廓线Fig.5 A heteromorphic ellipse on the xOy coordinate plane and the contour in top view 由图5、式(9)和式(13)可知,Ⅱ型异形椭球面的俯视轮廓异形椭圆与在xOy坐标面上的剖面异形椭圆非常接近,两者具有相同的对称轴长度(2a)和横向最大宽度对应的纵向坐标(xw=2a/e),横向坐标y1≈0.971yb(仅相差2.94%)。 4) Ⅱ型异形椭球面左、右、前、后、下和上的6个顶点坐标分别为(0,0,0)、(2a,0,0)、(2a/e,-b,-0.264c)、(2a/e,b,-0.264c)、(2a/e,0,-c)和(2a/e,0,c)。 5) 由异形椭圆面积系数分布曲线[9]可知,Ⅱ型异形椭球面的所有横截面异形椭圆半高度以下面积均占同一横截面总面积的55.61%。由此可知,Ⅱ型异形椭球体在xOy坐标面的上半部分与下半部分的体积比约为0.8∶1。 综上,在笛卡尔坐标系中,Ⅱ型异形椭球面的基本几何特征为:在yOz平行面、xOy和xOz坐标面上的剖面曲线以及俯视轮廓线均为异形椭圆;关于坐标面xOz对称;上半部分体积小于下半部分体积;在对称轴Ox的O端钝胖,远端锐瘦;下部宽大、底部较平坦,上部瘦小、顶部稍尖瘦,形心较低,稳定性好等特点。 三维空间Ⅰ型和Ⅱ型异形椭球面可以选择整体或分段与其它曲面组合应用,也可以选择从纵向坐标xw=2a/e的最大横截面位置截断,在中间增加一段最大横截面的“柱体段”,组合形成拟应用对象,以便获得更大的主体段功用空间。Ⅰ型和Ⅱ型异形椭球面可以任意选择纵向长度、横向宽度和垂向高度3个独立参数的数值大小和比例关系。限于篇幅和专业技术,下面对Ⅰ型和Ⅱ型异形椭球面(包括组合体曲面)的应用前景进行探讨,暂不涉及结构分析、外形参数和流体力学特性等。 1) 蛋形曲面建筑 仿生建筑由来已久,世界各国蛋形仿生建筑屡见不鲜[4]。异形椭圆本身就是一个自然图形[7],根据Ⅰ型和Ⅱ型异形椭球面的几何特征以及拟设计的建筑功用需求,合理选择纵向长度、横向宽度和垂向高度以及笛卡尔坐标系的方向,就可以设计出个性独特的Ⅰ型或Ⅱ型异形椭球面建筑造型。该类设计的建筑规模可大可小,可设计成体育场馆、大剧院、展览馆等,也可设计成住宅、别墅、现代“蒙古包”等。 如果选择对称轴Ox向上,Ⅰ型异形椭球面可以设计成高层摩天楼和塔楼的建筑造型,纵向坐标0 2) 民用飞机 民用客机机身截面一般分为两种,圆形与多圆弧。圆形截面由一个完整的圆构成,受力特性好,但空间利用率较低。多圆截面由多段圆弧和与其相协调的光滑过渡曲线组成,空间利用率高,但采用 AUTOCAD 软件进行作图,效率低,无法自动优化[11]。 Ⅰ型和Ⅱ型异形椭球面均具有独立3参数数学方程,可自动优化满足约束条件的设计方案。按照Ⅱ型异形椭球面方程构建的方法步骤,就能够更好地实现典型倒“8”字形机身截面和四段圆弧光滑过渡形机身截面[12]以及飞机后机身尾段截面[13]的参数化设计方法。 3) 船舶 科学研究与工程实践表明,船舶形状的优化设计对降低应力集中程度、获得精细化的结构形状、减小航行阻力、降低运输成本等,具有较高的应用价值[14-15]。 对船舶而言,采用倒置Ⅱ型异形椭球形(见图6),既可以实现船体轮廓曲面的平顺光滑,又可以获得更大的上部功用空间,便于客舱布置与货物装载。 图6 倒置Ⅱ型异形椭球体的三维建模网格剖面Fig.6 3D modeling grid profile of the inverted type II heteromorphic ellipsoid 倒置Ⅱ型异形椭球体上半部分与下半部分的体积比约为1∶0.8,浮心较高,下部为集中设备安装和动力层,形心较低,有利于船舶处于稳定平衡状态。 4) 工艺品 Ⅰ型和Ⅱ型异形椭球面方程都具有可任意调整的3个独立参数,可变换的形状众多,图案具有单轴对称性,钝胖端与锐瘦端区分明显,异形椭圆最大宽度位置接近黄金分割比例,使图形产生美感,适合做工艺品设计。 在对称轴半高度等于横向半宽度(即旋转半径)条件下,图7给出a=b=c=50 mm Ⅰ 型异形椭球体的3D打印样品(Wu’s夜明珠),它比球形摆放稳定性好。在对称轴纵向长度2a=55 mm、横向宽度2b=32 mm和垂向高度2c=9 mm条件下,图8(a)(b)给出Ⅱ型异形椭球形吊坠的三维设计图案和3D打印样品,其造型美观大方。 图7 a=b=c的Ⅰ型异形椭球体Fig.7 Type I heteromorphic ellipsoid with a=b=c 图8 Ⅱ型异形椭球形吊坠Fig.8 Pendant in the shape of a type II heteromorphic ellipsoid 1) 基于三维对流扩散物质的等浓度面方程,定义了包含半长度、 半宽度和半高度3个独立参数的Ⅰ型异形椭球面方程,给出在yOz平行面上的横截面为椭圆,在xOy和xOz坐标面上的剖面曲线均为异形椭圆的几何特征。 2) 将只有单对称轴的二维异形椭圆在三维空间进行推广,构建了三参数Ⅱ型异形椭球面方程,给出在yOz平行面、xOy和xOz坐标面上的剖面曲线以及俯视轮廓线均为异形椭圆、关于坐标面xOz对称、上半部分与下半部分的体积比约为0.8∶1的几何特征。 3) 分析表明,Ⅰ型和Ⅱ型异形椭球面的连续性、光滑性和整体性好,可以选择整体或分段组合应用于蛋形曲面建筑、民用飞机、船舶形状优化和工艺品等设计,具有很好的科学研究和应用前景。 致谢3D打印样品由青岛理工大学兰红波教授团队提供技术支持,硕士研究生祝帅举、任鹏绘制了三维建模图。3 Ⅱ型异形椭球面
3.1 基本思路
3.2 方程构建
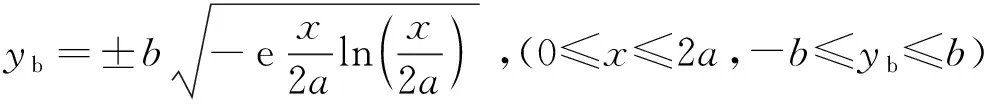
3.3 几何特征分析
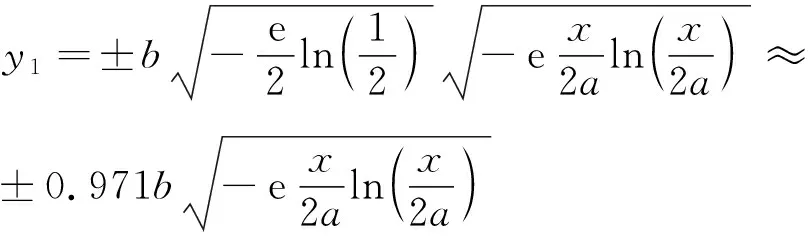
4 应用前景


5 结 论

