分贝的简便估算和应用

万果果，王恩华

（河南广播电视台卫星传输中心，河南 郑州 450000）

引言

从事广播电视技术工作的朋友们对“分贝dB”一定相当熟悉。dBx（x 代指各种单位后缀）家族无比兴旺，例如dBW、dBV、dBu、dBi、dBc、dBHz、dBFS、dBSPL等，它们在工作中随处可见，其中关系错综复杂，仅凭一篇短文实难尽述。本研究主要从科普和实用的角度，对dB 的概念及其应用进行讲述和分析，希望对读者理解和使用分贝有所帮助。

1 分贝的概念

从字面上看dB（decibel）就是十分之一贝尔，我们称之为“分贝”，而B（Bel）则是dB 的标准单位。B（Bel）是1928 年由贝尔系统为纪念电话的发明者亚历山大·格拉汉姆·贝尔所定义的，1931 年美国国家标准化局将dB 收录进标准化年鉴。由于B 的单位太大，在实际工作中以B 为单位会出现大量的小数数值，为便于使用常采用dB 作为常用单位。例如，发射机功率2 000 W，如需增加500 W，用B 表示时即增加0.1 B，若用dB 表示即增加1 dB，使用dB 更便捷。

从本质上讲，dB 是用对数表示两个量的比值。我国将dB 作为法定计量单位中非国际单位制的级差单位，定义为“两个同类功率量或可与功率类比的量之比值的常用对数乘以10 等于1 时的级差”。

2 对数的定义

谈分贝必然离不开对数（logarithm）。1594 年约翰·奈皮尔（John Napier）为了把当时的天文学家从极其复杂的计算中解救出来，在简化球面三角计算的过程中偶然将等差序列和等比序列进行对应，于是便构造出了对数。经过20 年的打磨，1614 年奈皮尔的《奇妙的对数定律说明书》在爱丁堡问世，向世人展示了对数的神奇力量。1637 年笛卡尔发明指数，比对数晚了23 年。然而，直到1770 年才由欧拉提出“对数源于指数”。

对数的神奇之处在于能把高级运算降为次级运算，即变乘除为加减，变乘方开方为乘除，并通过查对数表快速得到答案。在电子计算机出现之前的3 个多世纪，对数方法和对数表、对数尺（见图1）就是计算界的外挂。尽管计算机后来取代了对数表和对数尺，但是对数方法却在各行各业持续发扬光大。拉普拉斯评价说，对数可以缩短计算时间，在实效上等于把天文学家的寿命延长了许多倍。恩格斯在《自然辩证法》中把对数、解析几何和微积分共同称为17 世纪的三大数学发明。这都体现了对数的重要性，如果说对数造福了天文学家，那么基于对数的分贝则造福了工程技术人员。

图1 dBW-W 转换对数尺

3 分贝的意义

分贝就是常用对数的一种应用，因此也继承了对数的优点。首先，可以简化读写，例如C 频段卫星上行链路空间损耗[1]l=（4πd/λ）2，以6G 频率为例损耗约为8.186×1019倍，用分贝表示则记作损耗约199.13 dB，大大提高了可读性，又降低了出错的风险；其次，可以简化运算，将运算降级，例如4 0004×11 220，可写作4×10 lg（4 000）+10 lg（11 220）=144 dB+40.5 dB，降低了计算难度。

在声学领域，采用分贝表示声音的大小，更符合人的听感。例如功率从1 W 调至11 W 时听到的音量变化明显，而功率从100 W 调至110 W 时感觉音量几无变化，从数值上看功率同样增加10 W，但听感却大不相同，用分贝表示相当于分别增加了约10.4 dB和0.4 dB，相较功率，分贝反映的响度[2]变化更符合人的听觉感受。

4 分贝的速算方法

日常工作中，对功率的增减通常用dB 描述。例如当前功率为500 mW，增加8 dB 等于多少mW 呢？通常，以dB 为单位进行增减调节时多用整数，通过计算和对结果取近似值（便于心算），可以得到以下估算规律（见表1），其中计算值按公式10(n+x)÷10/10n÷10（n 为任意功率的dB 值，x 可以为增加或减去的dB 值）计算，保留4 位小数。

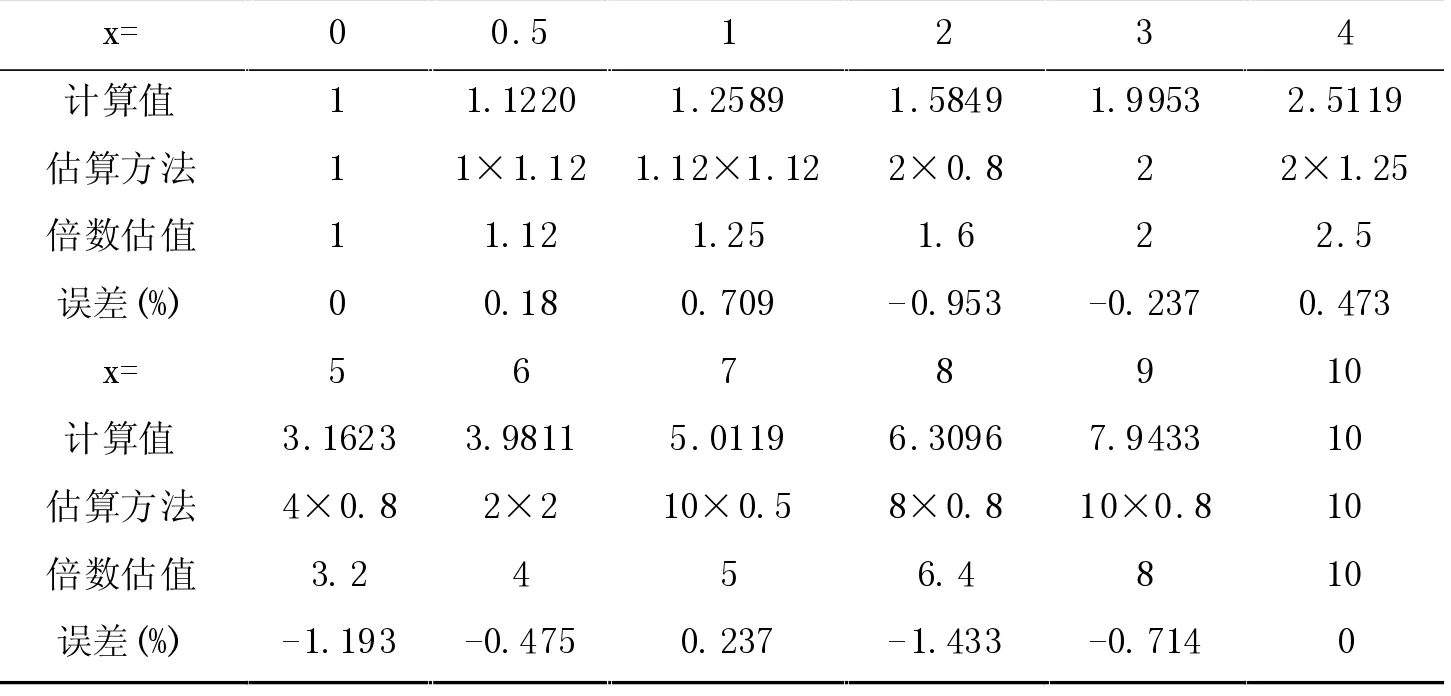
表1 +xdB 时的快速估算法

这就是前辈师傅传授的+3 dB 翻1 倍，+10 dB 翻10 倍的来历了。为了更好用，再扩展一下，+0.5 dB 约为1.12 倍，+1 dB 约为1.25 倍，-1 dB 约为0.8 倍，+2 dB 约为1.6 倍或者先翻1 倍再乘0.8，+5 dB 约为3.2倍或者翻2 倍再乘0.8，+7 dB 约为5 倍等。再看前面的问题，500 mW 增加8 dB，可以差分成7 dB+1 dB（相当于先乘5 再乘1.25），还可以拆分成9 dB-1 dB（相当于先乘8 再乘0.8），也可以直接乘6.4，实际估算时可根据数值灵活选取更方便的计算方法。-xdB时可用（10-x）dB 的近似估值除以10 进行计算，例如-1 dB 时10-1=9 dB，+9 dB 约为8 倍，除以10 为0.8，即-1 dB 约为0.8 倍，-0.5 dB 约为0.89 倍。如果计算的是幅度值则要先x/2，再以此进行估算。

表1 快速估算的最大误差为-1.433%，基本满足一般场景的应用。待熟练后，计算大数时可根据误差对估算结果进行补充，使其更接近实际值。还是前面的例子，初始功率为500 mW，显然乘8 再乘0.8 更好算，约等于3 200 mW，-1 dB 和+9 dB 的估算误差都是-0.714 %（负数表示估算值大于实际值），根据误差率，乘8 后差不多每1 000 mW 误差7 mW，500×8=4 000 mW 时产生约28 mW 的误差，4 000×0.8=3200 mW 时产生约21 mW 的误差，累积误差49 mW，3 200-49=3 151 mW 与实际计算值3 154.8 mW 近似。事实上，如果我们努力下，记住+8 dB 约等于6.3 倍，就可以直接心算500×6.3=3 150 mW。

反之，把500 mW 转换为dBm，可先拆分为100 mW×5=20 dBm+7 dB=27 dBm。有兴趣可以仔细观察表1 或者自己算一算，相信会有更多发现。

5 分贝的应用

5.1 表示倍数

分贝是无量纲，没有绝对意义，但可以用来表示倍数关系。参与功率增益计算时dB=10 lg（P1/P2），当参考基准P2=1 时可简化为dB=10 lg（P1），参与幅度增益计算时dB=20 lg（A1/A2），当参考基准A2=1 时可简化为dB=20 lg（A1）。当dB≥0 时，倍数≥1；dB＜0 时，0＜倍数＜1。例如：可以说功率增加3 dB，也可以说功率增加1 倍，二者等效。

dB 运算的实际意义如下：dB+dB，两级放大；-dBdB，两级衰减；dB-dB，先放大再衰减。

5.2 表示功率

常用功率单位有dBW[3]和dBm（dBmW）。dBW 的参考基准是1 W，即dBW=10 lg（P/1W），0 dBW=1 W；dBm 的参考基准是1 mW，即dBmW=10 lg（P/1 mW），0 dBm=1 mW。dBW 和dBm 仅单位词头不同，其换算关系为：0 dBW=30 dBm。

由P=UI 和I=U/R，可得P=U2/R，在不同的系统中R 的取值不同。通常在音频系统R=600 Ω，有线网络R=75 Ω，射频系统R=50 Ω，当P=1 mW 时，不同阻值对应的电压分别是0.775 V、0.274 V、0.224 V。

功率单位dBW（或dBm）和dB 有如下关系：

dBW（或dBm）+dB，功率增益；

dBW（或dBm）-dB，功率衰减；

dBW（或dBm）-dBW（或dBm），功率比；

dBW（或dBm）+dBW（或dBm），无现实意义。

5.3 表示电压

常用电平单位有dBV、dBmV、dBμV，对应的基准电压分别是1 V、1 mV、1 μV。由dBm=10 lg（P/P0）=10lg(（U2/R0）/(/R0))=10 lg（U/U0）2=20lg（U/U0）可知，使用dB 表示电压时应为20 lg（U/U0），那么dBV=20 lg（U/1 V），dBmV=20 lg （U/1 mV），dBμV=20 lg（U/1μV），1 V=1 000mV=1 000 000μV，0 dBV=60 dBmV=120 dBμV。由P=U2/R 可得dBW=10 lg（P/1W）=10 lg（U2/R）=10 lgU2-10 lgR=20 lgU-10 lgR，而dBV=20 lgU，代入得dBW=dBV-10 lgR，10 lg600=27.78，10 lg75=18.75，10 lg50=16.99，当功率为0 dBW 时和dBV、dBmV、dBμV 的换算见表2。

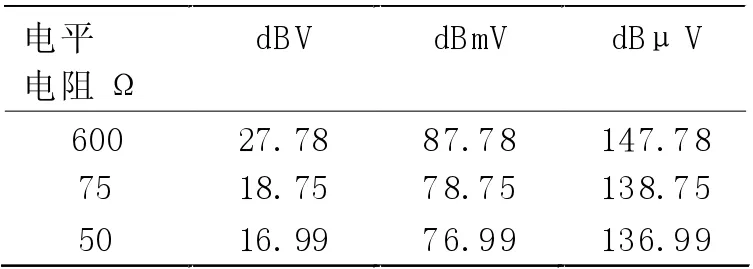
表2 功率0 dBW 不同电阻对应电平值

dBv 和dBu 可认为是同一个单位，而dBV 和dBv是不同的单位，因为dBV 和dBv 在书写时容易混淆，所以使用dBu 以便区分。dBu 主要用来表示音频领域中信号的幅度，电阻R=600 Ω，基准电压0.775 V，dBu=20 lg（U/0.775V）=20 lgU-20 lg0.775，代入可得dBu=dBV+2.218。

5.4 表示音量

前文提到用分贝表示声音的响度更符合人的实际听感，而人们在描述听到声音的大小时会说：“声音太大了，都有xx 分贝了”，准确来说这里的分贝指的就是dBSPL（Sound Pressure Level 声压级）或dBSIL（Sound Intensity Level 声强级）。

声压是大气压在受到声波扰动后产生的变化，和振幅相关，声压级dBSPL=20 lg（p/p0），p0取空气中人耳能够识别的最低声压2×10-5Pa 为参考基准。声强是通过垂直于声传播方向的单位面积上的平均声能量流，也叫平均声能量流密度。声强I=p2/z，p 是压强，z是空气阻力常量（取值400），当p=2×10-5Pa 时，I=0.000 022/400=10-12W/m2，声强级dBSIL=10 lg（I/I0），I为声强测量值，I0为常量（10-12W/m2）。由上述可知，声压为2×10-5Pa 时，声压级是0 dBSPL，声强级同样是0 dBSIL，理想情况下二者等效。所以，通常在说到某个声音的大小时，无论以dBSPL 还是dBSIL 为单位都是可以的，不过人们还是会习惯的只说“分贝”。值得注意的是0 dBSPL 或0 dBSIL 所表示的是人耳能够听到的最小的声音，而非没有声音。

dBFS（decibels relative to Full Scale）是相对于满幅度的分贝值，是专用于数字音频信号的电平单位。dBFS=20 lg（s/s0），参考基准s0是系统可以到达的最大值（不统一），因此0 dBFS 就是上限，所以除最大值外都是负数。例如某设备可以对模拟音频的幅度进行16 bit 量化，则s0=216=65 536，s 的最小值为1，计算可得最小音量为20 lg（1/65 536）=-96 dBFS，那么该设备的动态范围即96 dB[4]。

5.5 表示天线增益

dBi 和dBd 都是用来表示天线增益的相对值，区别是参考基准不同，它们之间可以进行相互转换。dBi（isotropic）是以理想点源全向天线为基准的增益，亦称为绝对增益或无方向增益；dBd（dipole）是以半波偶极子天线为基准的增益。半波偶极子天线的增益是全向天线的1.64 倍，即0 dBd=2.15 dBi。

6 结论

分贝（dB）作为表示两个同类量的级差单位，广泛应用于广播电视各技术部门，且采用dB+后缀的方式组成了诸多代表不同含义的新单位，而不同后缀前又可以+不同词头，这也造就了dBx 家族极其繁荣的场面，容易使人混淆和困惑。能够准确理解单位后缀和词头，明确是功率量还是幅度量，知悉基准值，理清相关单位间的关系和使用场景，才能实现dB 的使用自由。读者朋友亦可按本研究的思路对场强、功率密度等其它在工作中常用到的dB 单位进行分析和梳理，找到更多实用的信息和规律，为业务工作打牢基础。