基于学生发展指导的高中数学教学实践与思考

◎李小华 黄明春

(福建省晋江市紫峰中学，福建 晋江 362200)

教师在教学中不仅要关注学生学科知识的形成过程，而且要关注学生发展指导工作，在学生形成正确的人生观、价值观等方面发挥独特作用在数学课堂教学中，教师要基于高中数学知识，渗透学生发展指导思想，帮助学生做好学业规划、生涯规划，为学生的发展指引方向

一、挖掘教材资源，在数学教学中融入理想信念指导

教材是教师在教学中的重要依托，新教材中加入了“阅读与思考”栏目，介绍了在数学领域做出突出贡献的数学名人比如，我国古代数学家对某些类型方程求解的问题的贡献，南宋数学家秦九韶发现了由三角形求三面的面积公式，魏晋时期数学家刘徽在为《九章算术》所作的注文中给出了等差数列的求和公式，北宋数学家沈括开创了我国“垛积术”的研究，南宋数学家杨辉将堆垛与相应的立体图形进行类比，推导出了三角垛、方垛、刍甍垛、刍童垛等的公式教师还可以介绍中国现代数学领域的杰出人物，如：中国现代数学之父华罗庚，他在中国解析数论、矩阵几何学等领域为中国数学发展做出贡献；陈省身开创整体微分几何、纤维丛微分几何等，在微分几何上做出卓越贡献，影响着整个数学的发展；丘成桐对几何微分学和数学物理的发展做出重要贡献；吴文俊在拓扑学和数学机械化两个领域做出贡献；等等教师在教学过程中引导学生搜集和阅读中国数学名人的励志故事并与同学分享，增强学生的民族自尊心和自豪感，培养学生的爱国主义精神，激发学生学习的热情教师应在数学教学中充分挖掘学科教学中的人物素材，融入对学生的理想信念指导

二、关注学习规律，在数学教学中融入学业指导

学生进入高中阶段以后，突然感觉曾经那么拿手的数学学科一下变得陌生了，虽然他们还是像初中那样努力，却难以考到高分，甚至有时为了及格而苦苦挣扎高中数学与初中数学比较，有几个变化：一是课程断层，初高中课程衔接不畅；二是教材内容变化，初中教材通俗、具体、直观，具有趣味性，内容较为单一，知识容量小，高中教材数学符号多，具有抽象性，高中数学知识容量大，内容抽象性和概括性增强；三是教法不同，初中课堂容量较小，通过模仿再加以反复练习就可以掌握，高中课堂容量大，强调数学思想方法的运用，因此刚进入高中的学生不适应这种教学方法，从而产生学习障碍；四是学习方法改变了，初中更多是“被动模仿式”学习，不注重独立思考和对规律的归纳总结，而高中是“独立思考式”学习，需要养成独立思考、善于归纳总结规律、掌握数学思想方法的学习习惯，因此刚入学的高一新生往往沿用初中学法，不会独立思考，总是想套学习模式因此，教师在高中数学教学中需要融入学业指导，基于学情对高中课程框架、教法、方法以及学习成果，结合学生个人能力进行有针对性的指导

三、创新教学方式，在数学教学中融入生涯规划指导

中学阶段是学生认识自我的重要时期，教师要在数学教学过程中融入学生生涯规划指导，使学生树立职业规划意识，为高考选课做好准备

本文结合人教版数学必修第二册第十章《随机模拟》与软件工程师这一职业相结合，在教学中进行生涯规划渗透

环节一：创设情境，引入新课

思考：用频率估计概率,需要做大量的重复低效随机模拟试验，有没有其他途径可以得到我们想要的结果呢？

师：我们利用手中的计算器或Excel来生成随机数，通过具体情境搭建所对应的随机数模拟情境，这样可以高效完成试验

环节二：合作探究,构建新知

探究：一个箱子里装有5个仅颜色不同的球(两红和三白)对于从箱子里摸出一个球的试验,我们可以用Excel产生取值于集合{1，2，3，4，5}的随机数，用1，2代表红色球，用3，4，5代表白色球基于此产生1～5的随机整数，相当于不断地做在箱子里摸球的试验

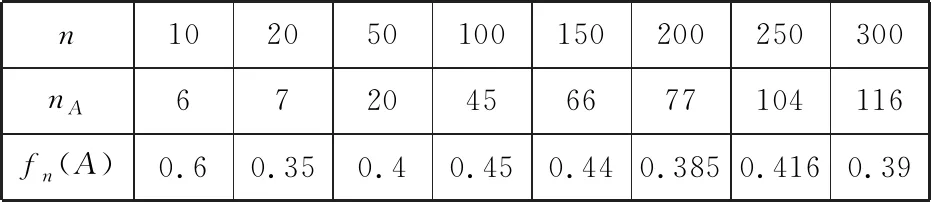
下表中是用Excel模拟上述摸球试验的结果，代表试验次数，为摸红色球的频数，()为摸到红色球的频率

n102050100150200250300nA6720456677104116fn(A)0.60.350.40.450.440.3850.4160.39

摸球频率折线图如下我们由图表可以发现：随着摸球试验模拟次数的增加，摸到红色球的频率趋于概率04

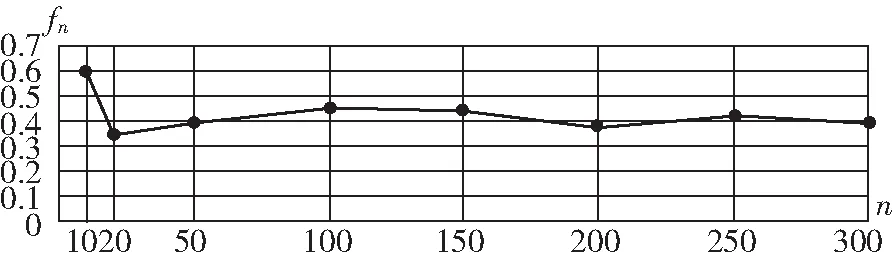
利用频率来估计概率，需要做大量的重复低效试验，但我们可以根据不同情境构建相应的随机数模拟试验，这样就能快速高效地完成大量重复试验

1从高一年级随机选出6名同学，调查他们的星座，假设出生的每个星座是等可能的设事件甲为“至少有两人星座相同”，设计一种试验方法，模拟20次实验，估算事件甲发生的概率

小组讨论:构建有放回摸球试验进行模拟，统计出事件甲发生的频率，用频率估计事件甲发生的概率

师：如果让同学们模拟100次？1000次？10000次呢？

学生表示还是可以通过摸球实验进行，但是效率太过低下

师：我们还可以用电子表格软件(Excel)进行随机模拟实验，在第一行的前6格使用函数“=RANDBETWEEN(1，12)”，随机生成6个数，对应6名同学的星座，本次随机模拟实验完成拉动鼠标至第100行，即完成100次重复试验Excel自动统计含有相同数字的频率，便可算出事件甲发生的概率

学生以小组形式通过Excel模拟1000次实验和10000次实验，Excel自动统计含有相同数字的频率，学生计算得出事件甲发生的概率

师小结：数学源于生活，我们可以通过数学的学习，掌握软件的应用，甚至开发出一款软件来服务于生活，帮助我们快速便捷地解决现实问题，函数RANDBETWEEN，实际上就是将我们随机模拟的数学思想融入编程，使得大多数人能够简单操作

课后延伸：你觉得我们还有什么数学思想或者算法可以融入编程，让我们更好地解决现实生活中的问题？

【设计意图】本例是随机模拟的实际应用，以学生所熟悉的出生月份为背景，通过摸球试验和电子表格模拟试验，学生自主探索，给予学生解决问题的自主权，促进生生、师生交流

2在冬奥会自由式滑雪比赛中，谷爱凌和凯茜·夏普双双进入了激动人心的决赛谷爱凌对战凯茜·夏普胜率为06，凯茜·夏普的胜率仅为04利用计算机VS2017平台进行随机模拟试验，估算谷爱凌夺冠的概率

运行程序，分别输入测试的数量500和1000，得到以下运行结果：

第一次共测试500组，谷爱凌获胜305组，她获胜的概率为061；第二次共测试1000组，谷爱凌获胜621组，她获胜的概率为062；……

基于VS平台使用主流C++编程语言自创模拟器，学生可通过该模拟器便捷快速地生成多组(20组、50组、100组等)随机数，并自动计算出谷爱凌的获胜概率.

【设计意图】 根据谷爱凌夺冠的时事设计题目，引起学生的学习兴趣，利用计算机模拟试验，采用基于VS平台使用C++编写程序，利用C++模拟器估计谷爱凌获得冬奥会自由式滑雪比赛冠军的概率教师利用新知识引导学生了解具体的职业，让学生对软件工程师这一职业有一定的了解和感性认识

环节三：职业体验，规划学业

小组讨论：要成为一名软件工程师需要具备哪些素质？学生结合职业体验时的感受，展开小组讨论

师小结：成为一名软件工程师需要具备需求分析能力、沟通能力、表达能力以及团队合作能力,根据目标用户的需求进行产品研发，能够与团队中的成员协同开发,共同完成任务；软件开发过程中需要对项目设计和流程进行处理，能够凭借现有资源以及甲方需求构建项目的最优整体设计，能够熟悉基本的软件开发流程和工具,能够正常迭代更新编程软件；使用计算编写功能代码，控制软件开发过程中的风险和BUG的修复，这对数学能力、逻辑思维、发现问题和解决问题的能力有较高的要求；具备英语阅读和书写的能力，要能够流畅地编写程序，掌握主流编程语言，能灵活运用数据结构，精通算法分析与设计以及编译原理

课后延伸：通过网络查找与软件工程师相关的大学、专业以及高中选考科目信息，为高二选科和职业规划奠定基础

【设计意图】体验代码编程应用，让学生体会软件开发工程师所需具备的基本素养，通过了解软件开发工程师所需要的职业基本技能，唤醒学生的职业体验，帮助学生挖掘自身素养，让学生根据自己的兴趣和理想选择职业，让学生明确各院校对应的专业、对应的选考科目要求，为学生的选科和学业规划提供指导

四、创设问题情境，在数学教学中融入生活实践指导

学生应通过高中数学课程的学习，学会用数学模型解决实际问题，积累数学实践经验，提升实践能力教师在课堂教学中创设恰当的生活情境，激发学生的学习兴趣，让学生体会到应用数学解决问题的乐趣生活中有大量的数学情境，如很多家庭利用闲余资金在银行存定期或购买理财产品，在贷款购房中采用等额本息还款或等额本金还款等下面我们以《购房中的数学问题》为例，通过问题引导，构建模型、推理计算来做出决策，让学生在实践探究中感受数学的应用价值

3某位居民家庭每月的总收入为5000元，为了改善家庭住房条件，男主人打算贷款购房若向银行贷款30万，贷款月利率为05%，计划20年还清，每年大概能还款3万元，有下面两种还款方案：

方案一,等额本金还款，每月还款金额=本金部分+利息部分；

方案二,等额本息还款，从贷款后第二期起，每期以相等的款额平均偿还贷款本金和利息

请大家帮忙计算一下,等额本金与等额本息两种还款方式每期应各还多少钱？你认为男主人应该选择哪种还款方案？

1教师设问引导

问题(1):在选择还款方案时,你应该主要考虑哪些因素？

问题(2)：你可以运用学过的知识描述各种还款方案的数量关系吗？

问题(3)：通过以上分析，你将做出怎样的还款选择？

2展示探究成果

分析数量关系，构建函数模型：设还款期数为，贷款本金为，第个月欠款为，每个月还款元，贷款月利率为

方案一：

期数n欠款额an本金偿还Rn利息偿还In还款额pn1300000125015002750229875012501493.752743.75︙n1250(241-n)12506.25(241-n)6.25(441-n)︙240125012506.251256.25

还款总额：(2750+125625)×240÷2=480750(元)

还款总额：2149294×240=51583056(元)

3解决实际问题

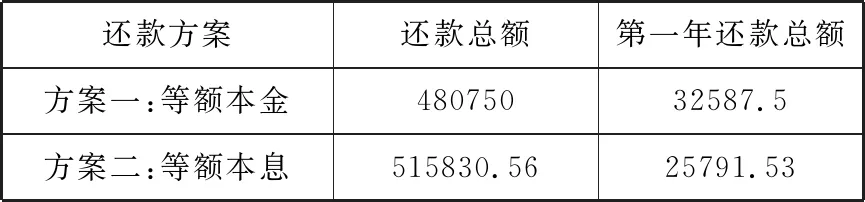
方案对比：

还款方案还款总额第一年还款总额方案一:等额本金48075032587.5方案二:等额本息515830.5625791.53

分析判断：要做出还款方案选择，除了要考虑还款的总额外，还需要考虑每个月还款的数额，在每年还款不超过三万元的条件下应该选择方案二因此，数学教师在教学中要挖掘课程资源，创设问题情境，培养学生的数学应用意识，让数学服务于生活，体现数学的应用价值

学生发展指导不能仅靠班主任和心理教师来开展，而应充分调动各学科教师在各自学科的教学中渗透学生发展指导，帮助学生做好学业、生涯规划等指导这样不仅能提升教师的学生发展指导意识和能力，而且能促进学生健康成长